- Учителю
- Урок на тему 'Сумма внутренних углов треугольника' (геометрия 7 класс)
Урок на тему 'Сумма внутренних углов треугольника' (геометрия 7 класс)
Тема: Сумма внутренних углов треугольника (7 класс)
Цель: сформировать и закрепить у учащихся знания о сумме внутренних углов треугольника, величине углов равностороннего треугольника.
Задачи:
Обучающие - сформировать и закрепить у учащихся знания о том, что сумма внутренних углов треугольника равна 180, сформировать и закрепить умения и навыки решения задач с применением знаний, полученных по теме урока.
Развивающие - уметь делать выводы; анализировать ход решения заданий;
развивать познавательные процессы, память, воображение, мышление, внимание, наблюдательность, сообразительность , умение самоорганизовываться.
Воспитательные - уметь ставить перед собой цель; уметь работать в группе, проявлять активность, обмениваться мнениями; уметь оценивать себя;
воспитывать культуру общения.
Тип урока: комбинированный
Оборудование: учебник, карточки, интерактивная доска, проектор, флипчарт «Сумма внутренних углов треугольника»
ХОД УРОКА
-
Организационный момент
-
Создание колоборативной среды Тренинг «Ручеек»
-
Деление по группам по виду треугольника, выбор спикера, оценочные листы.
-
Актуализация знаний учащихся
- Сегодня на уроке мы с вами снова вернемся к изучению треугольников. И, для начала, давайте повторим пройденный материал и вспомним некоторые понятия, которые пригодятся для изучения новой темы. Для этого мы с вами выполним ряд заданий.
-
Проверка домашнего задания по флипчарту
-
Поймай вопрос
«Тонкие вопросы»
-
Фигура, состоящая из трех точек, не лежащих на одной прямой, и трех отрезков, соединяющих эти точки, называется…(треугольник)
-
Треугольник, у которого все три стороны равны, называется…(равносторонним)
-
Треугольник, у которого две стороны равны, называется…(равнобедренным)
-
Как называется сторона прямоугольного треугольника, лежащая против прямого угла?
-
Как называется точка пересечения медиан? (Центр тяжести)
-
Треугольник, у которого один угол прямой, называется…(прямоугольный)
-
Как называется точка пересечения Высот? (ортоцентром)
-
Как называются стороны прямоугольного треугольника исходящие из прямого угла?
-
Чем является точка пересечения биссектрис треугольника? (центром вписанной окружности)
«Толстые вопросы»
1. Почему отрезок исходящий из вершины треугольника делит его угол пополам?
2. В каком случае треугольник называют тупоугольным?
3. Почему в треугольнике можно провести три медианы?
4. Когда треугольник называют остроугольным?
5. Почему отрезок, выходящий из вершины треугольника перпендикулярен его
основанию?
6.В каком случае треугольник называется разносторонним?
7. Согласны ли вы, что у треугольника можно провести три высоты? Почему?
Определение темы урока и ее постановка.
- Даны «Тематические слова, словосочетания или предложения», давайте посмотрим, что нам уже знакомо, а, что мы еще не знаем. То, что мы еще не знаем, и будет темой нашего урока.
-
Виды треугольников.
-
Биссектриса треугольника.
-
Внутренние накрест лежащие углы.
-
Сумма углов треугольника.
-
Развернутый угол.
-
Параллельные прямые.
Целепологание
2. Объяснение нового материала
-
Исследовательское задание
Учащимся раздаются 5 вариантов карточек с изображением треугольников разных видов. Дается задание с помощью транспортира измерить углы треугольника, записать полученные результаты и найти сумму градусных мер углов треугольника. Параллельно один ученик выполняет аналогичное задание на рабочей доске, другой на интерактивной доске.
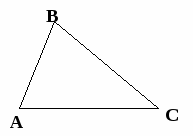
A =
B =
C =
A + B + C =
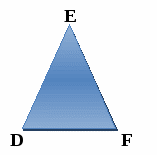
D =
E =
F =
D + E + F =
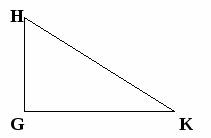
G =
H =
K =
G + H + K =
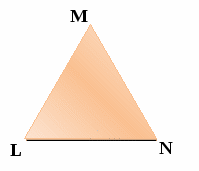
L =
M =
N =
L + M + N =
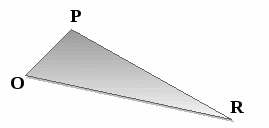
O =
P =
R =
O + P + R =
Вопрос классу: Как вы думаете, сумма углов треугольника зависит от его вида или длин сторон?
В результате измерений учащиеся приходят к предположению, что сумма углов треугольника, независимо от его вида, равна 180.
- Ребята, вы знаете, что в геометрии любое утверждение доказывается при помощи уже доказанных ранее фактов. Посмотрите внимательно на заключение теоремы. Нам необходимо доказать, что сумма углов треугольника равна 180°. А в каких, изученных ранее фактах, мы сталкивались с числом 180°?
Возможные варианты ответов учащихся:
1. Развернутый угол равен 180°
2. Сумма смежных углов равна 180°.
3. Если две параллельные прямые пересечены третьей, то сумма внутренних односторонних углов равна 180°.
- Так как смежные углы в сумме образуют развернутый угол, то предлагаю 1) и 2) варианты рассматривать как один факт: Развернутый угол равен 180°.
-
Практическое задание.
Используя бумажную модель треугольника, продемонстрируйте, как можно использовать сведения о развернутом угле, при доказательстве нашей теоремы.
(Большинство учащихся, скорее всего, догадается оторвать два угла треугольника и приложить их к третьему, в результате чего они образуют развернутый угол. )
- Предложенный способ доказательства можно считать практическим доказательством теоремы.
У нас остался еще один изученный ранее факт: Если две параллельные прямые пересечены третьей, то сумма внутренних односторонних углов равна 180°.
Предлагаю доказать теорему теоретически на основе этого факта.
Теорема: Сумма внутренних углов треугольника равна 180.
Дано:
АВС
Д оказать: А+В+С=180
оказать: А+В+С=180
Д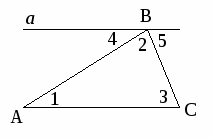 оказательство:
оказательство:
Через вершину В проведем прямую а, параллельную АС.
Пусть АВ - секущая, тогда 1=4, как накрест лежащие углы. Если ВС считать секущей, 3=5, как накрест лежащие углы.
Углы 4, 2 и 5 образуют развернутый угол, значит 4+2+5=180. Заменим углы 4 и 5 равными им углами, тогда 1+2+3=180, т. е. А+В+С=180
Терема доказана.
-
Решение задач на закрепление
-
Работа в группах
1,2 - 1 группа
3,4 -2 группа
5,6 -3 группа, 7 - всем классом
№
А
В
С
вид треугольника
60
60
? (60)
? (равносторонний)
? (90)
30
? (60)
прямоугольный
35
? (35)
110
? (тупоугольный, равнобедренный)
? (70)
? (40)
70
равнобедренный
100
30
? (50)
? (остроугольный)
? (50)
75
55
? (остроугольный)
? (45)
90
45
? (прямоугольный, равнобедренный)
Работа с учебником. Стр. 49 №149 (4)
(Решение у доски, запись в тетрадях)
-
Работа в парах стр.49 №149
(взаимопроверка)
Р ешение по рисунку у доски (1 ученик)
ешение по рисунку у доски (1 ученик)
-
Индивидуальная работа по разноуровневым карточкам.
-
Решение по образцу.
-
Решение по готовому чертежу.
-
Решение по алгоритму.
Самопроверка по интерактивной доске.
4. Тест таблица «Да-Нет»
Условные обозначения «да»- ^, «нет»-_.
-
Сумма углов треугольника всегда равна 180 градусам.
-
Существует треугольник с углами 100, 80 и 10 градусов.
-
В треугольнике может быть два тупых угла.
-
Все углы треугольника могут быть острыми.
-
Можно найти один из углов треугольника, если известны два других.
-
Острый угол прямоугольного треугольника можно найти, если известна величина второго острого угла.
-
Угол при основании равнобедренного треугольника может быть тупым.
-
Угол при вершине равнобедренного треугольника может быть тупым.
-
Если один угол треугольника равен 100 градусам, другой - 30 градусам, тогда третий угол равен 50 градусам.
-
Можно найти неизвестный угол произвольного треугольника, если дан только один его угол.
Ключ: ^_ _^^^_^^_ (взаимопроверка)
Самооценка:
без ошибок-«5»;
1-2 ошибки- «4»;
3-4 ошибки-«3»;
более 4 ошибок-«2».
5.Подведение итогов
-
Работа с оценочными листами
-
Выступление спикеров
6.Задание на дом
Читать п12, Теорема1, стр 50 № 155 или №156
-
Рефлексия.
№
А
В
С
вид треугольника
1
60
60
2
30
прямоугольный
№
А
В
С
вид треугольника
1
35
110
2
70
равнобедренный
№
А
В
С
вид треугольника
1
100
30
2
75
55
Оценочный лист
Ф.И. ученика
1№
Задание
Критерии оценивания
Набранный балл
11
Поймай вопрос
Паравильный ответ 1 балл
2
Дополнительные ответы
Верный ответ 1 балл
3
Исследовательская работа
Правильное построение 1 балл
Вывод 1 балл
4
Перепутанные логические цепочки
За участие 1 балл
Выступление 1 балл
5
Практическое задание
Правильное выполнение 1балл
6
Заполнение таблицы
Участие 1 балл
7
Решение у доски
2 балла
8
Работа в парах
За верное решение 2 балла
9
Работа по карточкам
10
«Да-Нет»
Итого баллов
Оценка
Оценочный лист
Ф.И. ученика
1№
Задание
Критерии оценивания
Набранный балл
11
Поймай вопрос
Правильный ответ 1 балл
2
Дополнительные ответы
Верный ответ 1 балл
3
Исследовательская работа
Правильное построение 1 балл
Вывод 1 балл
4
Перепутанные логические цепочки
За участие 1 балл
Выступление 1 балл
5
Практическое задание
Правильное выполнение 1балл
6
Заполнение таблицы
Участие 1 балл
7
Решение у доски
2 балла
8
Работа в парах
За верное решение 2 балла
9
Работа по карточкам
10
«Да-Нет»
Итого баллов
Оценка
Задание на дом
-
Читать п12, Теорема1, стр 50 № 155 или №156
-
Презентация
-
Карточки (на выбор).