- Учителю
- Методическое пособие Математика для учащихся старших классов
Методическое пособие Математика для учащихся старших классов
ФГАОУ ВО «КРЫМСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ имени В.И. Вернадского» ГУМАНИТАРНО-ПЕДАГОГИЧЕСКАЯ АКАДЕМИЯ (ФИЛИАЛ) В Г. ЯЛТЕ
ИНСТИТУТ ЭКОНОМИКИ И УПРАВЛЕНИЯ
Бубнова А.А.
МЕТОДИЧЕСКОЕ ПОСОБИЕ
МАТЕМАТИКА
для студентов-бакалавров
Ялта, 2016
УДК 51(07)
ББК 22.1я73
Б 90
Рекомендовано ученым совета Гуманитарно-педагогической академии (филиал) «Крымский федеральный университет им. В.И. Вернадского» от «8» декабря 2015 года (протокол № 11)
Бубнова А.А.
Б 90 Математика. / Бубнова А.А.:
Методическое пособие. - Ялта: РИО ГПА, 2016. - 56с.
Данное пособие предназначено для студентов математических и экономических специальностей, для учащихся старших классов, учителей школ и преподавателей вузов. Пособие содержит программный материал по математике. Может быть использовано для подготовки к экзамену по математике и единому государственному экзамену.
Рецензенты:
Орлов В.Н., доктор физико-математических наук, профессор кафедры математики, теории и методики обучения математике Гуманитарно-педагогической академии (филиал) в г. Ялте «Крымского федерального университета им. В.И. Вернадского».
Овчинникова М.В., кандидат педагогических наук, доцент кафедры математики, теории и методики обучения математике Гуманитарно-педагогической академии (филиал) в г. Ялте «Крымского федерального университета им. В.И. Вернадского».
ББК 22.151.54
©Бубнова А.А., 2016 г.
©Гуманитарно-педагогическая академия (г. Ялта), 2016 г.
СОДЕРЖАНИЕ
ВВЕДЕНИЕ 4
1. ЧИСЛОВЫЕ СИСТЕМЫ 5
- Различные числовые множества. Метод математической индукции 5
- Действия над действительными числами 12
- Модуль числа. Числовая прямая 16
- Отношения. Пропорция. Проценты 18
2. ФУНКЦИИ 20
- Определение, виды и свойства функций 20
- Построение графиков элементарных функций 20
- Тригонометрия 27
3. ПРОИЗВОДНАЯ И ИНТЕГРАЛ 27
- Производная, таблица производных 27
- Первообразная. Таблица интегралов 32
- Определённый интеграл. Формула Ньютона-Лейбница 32
4. КОМБИНАТОРИКА 34
- Перестановки, размещения и сочетания без повторений 34
- Перестановки, размещения и сочетания с повторениями 35
- Бином Ньютона 36
5. СТАТИСТИКА 37
- Сбор информации для статистики 37
- Вариационный ряд. Распределение ряда 37
- Математические параметры статистического распределения 38
6.СПРАВОЧНЫЙ МАТЕРИАЛ 41
7.ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ 42
8. ВОПРОСЫ К ЭКЗАМЕНУ. ВАРИАНТ КОНТРОЛЬНОЙ РАБОТЫ 53
ЛИТЕРАТУРА 55
ЭЛЕКТРОННОЕ ПРИЛОЖЕНИЕ
ВВЕДЕНИЕ
Дисциплина «Математика» является одной из базовых дисциплин в программе Высшей школы. Целями этой учебной дисциплины являются:
- формирование у студентов представления об общих математических понятиях;
- приобретение студентами теоретических знаний, практических умений и навыков, необходимых для осуществления в будущем педагогической деятельности на высоком профессиональном уровне.
Данное пособие написано в соответствии с программой курса «Математика» и состоит из восьми разделов: «Числовые системы», «Функции», «Производная и интеграл», «Комбинаторика», «Статистика», «Справочный материал», «Задания для самостоятельной работы», «Вопросы к экзамену и вариант контрольной работы».
Раздел «Числовые системы» освещает вопросы: понятия различных числовых множеств, арифметические действия над действительными числами и их свойств; понятия процента и решения задач на проценты.
Раздел «Функции» рассматривает: различные виды функций их свойств и построение их графиков.
Раздел «Производная. Интеграл» содержит вопросы: определение предела функции, производной функции, первообразную и интеграл.
В раздел «Комбинаторика», «Статистика» рассматриваются определения и формул различных комбинаций, формула бинома Ньютона, методы статистических.
В пособии предложены задания для самостоятельной работы, а также темы для подготовки к экзамену по дисциплине «Математика».
В пособии имеются индивидуальные задания, позволяющие студентам привести свои знания по теме в систему и приобрести практические умения в ходе решения поставленных перед ними конкретных методических задач.
Пособие снабжено электронным приложением, в котором есть 30 видеоуроков, 50 презентаций по разделам математики. Читатели свои знания могут проверить с помощью 44 тестов. В приложении есть наглядный справочный материал в таблицах и графиках.
Пособием могут пользоваться студенты как заочного, так и дневного обучения. Преподаватель может использовать материал пособия для составления дидактического материала. Ученики старших классов могут по этому пособию готовиться к олимпиадам, а так же к единому государственному экзамену.
1. ЧИСЛОВЫЕ СИСТЕМЫ
Различные числовые множества
Основные понятия
Понятие множества является одним из основных неопределяемых понятий математики. Под множеством понимают совокупность (собрание, класс, семейство...) некоторых объектов, объединенных по какому-либо признаку. Так можно говорить о множестве студентов института, о множестве рыб в Черном море, о множестве корней уравнения х2+2х+2=0, о множестве всех натуральных чисел и т. д.
Объекты, из которых состоит множество, называются его элементами. Множества принято обозначать заглавными буквами латинского алфавита А, В,..., X, Y,..., а их элементы - малыми буквами a, b,... ...,х,у,...
Если элемент х принадлежит множеству X, то записывают х ÎX; запись хÏХ или х ÎX означает, что элемент х не принадлежит множеству X.
Множество, не содержащее ни одного элемента, называется пустым, обозначается символом Ø.
Элементы множества записывают в фигурных скобках, внутри которых они перечислены (если это возможно), либо указано общее свойство, которым обладают все элементы данного множества.
Например, запись А={1,3,15} означает, что множество А состоит из трех чисел 1, 3 и 15; запись А={х:0≤х≤2} означает, что множество А состоит из всех действительных (если не оговорено иное) чисел, удовлетворяющих неравенству 0 ≤ х ≤ 2.
Множество А называется подмножеством множества В, если каждый элемент множества А является элементом множества В. Символически это обозначают так АÌВ («А включено в В») или ВÉА («множество В включает в себя множество А»).
Говорят, что множества A и В равны или совпадают, и пишут А=В, если АÌВ и ВÌА. Другими словами, множества, состоящие из одних и тех же элементов, называются равными.
Объединением (или суммой) множеств A и В называется множество, состоящее из элементов, каждый из которых принадлежит хотя бы одному из этих множеств. Объединение (сумму) множеств обозначают AUВ (или А+В). Кратко можно записать АUВ={х:хєА или хєВ}.
Пересечением (или произведением) множеств А и В называется множество, состоящее из элементов, каждый из которых принадлежит множеству А и множеству В. Пересечение (произведение) множеств обозначают А∩В (или А*В). Кратко можно записать А∩В={х:хєА и хєВ}
В дальнейшем для сокращения записей будем использовать некоторые простейшие логические символы:
ΑÞ ß - означает «из предложения α следует предложение ß»;
ΑÛ ß - «предложения α и ß равносильны», т. е. из α следует ß и из ß следует α;
" - означает «для любого», «для всякого»;
$ - «существует», «найдется»;
: - «имеет место», «такое что»;
→ - «соответствие».
Например:
1) запись " xÎ А:α означает: «для всякого элемента хÎ А имеет место
предложение α»;
2) (х єA U В) <==> (х є А или х є В); эта запись определяет
объединение множеств А и В.
Числовые множества
-
Числа вида N = {1, 2, 3, ....} называются натуральными. Натуральные числа появились в связи с необходимостью подсчета предметов
-
Если m, n, k - натуральные числа, то при m - n = k говорят, что m - уменьшаемое, n - вычитаемое, k - разность; при m : n = k говорят, что m - делимое, n - делитель, k - частное, число m называют также кратным числаn, а число n - делителем числа m, Если число m - кратное числа n, то существует натуральное число k, такое, что m = kn.
-
Из чисел с помощью знаков арифметических действий и скобок составляются числовые выражения. Если в числовом выражении выполнить указанные действия, соблюдая принятый порядок, то получиться число, которое называется значением выражения.
-
Порядок арифметических действий: сначала выполняются действия в скобках; внутри любых скобок сначала выполняют умножение и деление, а потом сложение и вычитание.
-
Если натуральное число m не делится на натуральное число n, т.е. не существует такого натурального числа k, что m = kn, то рассматривают деление с остатком: m = np + r, где m - делимое, n - делитель (m>n), p - частное, r - остаток.
-
Если число имеет только два делителя (само число и единица), то оно называется простым: если число имеет более двух делителей, то оно называется составным.
-
Любое составное натуральное число можно разложить на простые множители, и только одним способом. При разложении чисел на простые множители используют признаки делимости.
-
Для любых заданных натуральных чисел a и b можно найти наибольший общий делитель. Он обозначается D(a,b). Если числа a и b таковы, что D(a,b) = 1, то числа a и b называются взаимно простыми.
-
Для любых заданных натуральных чисел a и b можно найти наименьшее общее кратное. Оно обозначается K(a,b). Любое общее кратное чисел a и b делится на K(a,b).
-
Если числа a и b взаимно простые, т.е. D(a,b) = 1, то K(a,b) = ab .
-
Числа вида: Z = {... -3, -2, -1, 0, 1, 2, 3, ....} называются целыми числами, т.е. целые числа - это натуральные числа, числа, противоположные натуральным, и число 0.
Натуральные числа 1, 2, 3, 4, 5.... называют также положительными целыми числами. Числа -1, -2, -3, -4, -5, ...,противоположные натуральным, называются отрицательными целыми числами.
-
Целые и дробные числа составляют множество рациональных чисел: Q = Z
 {n/m}, где
m - целое число, а n -
натуральное число.
{n/m}, где
m - целое число, а n -
натуральное число.
-
Среди дробей, обозначающих данное рациональное число, имеется одна и только одна несократимая дробь. Для целых чисел - это дробь со знаменателем 1.
-
Каждое рациональное число представимо в виде конечной или бесконечной периодической десятичной дроби.
-
Дробь n/m называется правильной, если ее числитель меньше знаменателя, и неправильной, если ее числитель больше знаменателя или раен ему.
-
Всякую неправильную дробь можно представить в виде суммы натурального числа и правильной дроби.
-
Основное свойство дроби: если числитель и знаменатель данной дроби умножить на одно и то же натуральное число, то получится дробь, равная данной.
-
Если числитель и знаменатель дроби взаимно простые числа, то дробь называется несократимой.
-
В виде десятичной дроби можно записать правильную дробь, знаменатель которой равен степени с основанием 10. Если к десятичной дроби приписать справа нуль или несколько нулей, то получится равная ей дробь. Если десятичная дробь оканчивается одним или несколькими нулями, то эти нули можно отбросить - получиться равная ей дробь. Значимыми цифрами числа называются все его цифры, кроме нулей, стоящих в начале.
-
Последовательно повторяющаяся группа цифр после запятой в десятичной записи числа называется периодом, а бесконечная десятичная дробь, имеющая такой период в своей записи, называется периодической. Если период начинается сразу после запятой, то дробь называется чистой периодической; если же между запятой м периодом есть другие десятичные знаки, то дробь называется смешанной периодической.
Числа не являющиеся целыми или дробными называются иррациональными.
Каждое иррациональное число представляется в виде непериодической бесконечной десятичной дробью
Множество всех конечных и бесконечных десятичных дробей называется множеством действительных чисел: рациональных и иррациональных
Действительные числа

Замечание. Любое рациональное число - бесконечная периодическая десятичная дробь
Иррациональные числа. Числа,
которые нельзя представить в виде nmm![]() Z
Z![]() n
n![]() N,
называют иррациональными. I = {
N,
называют иррациональными. I = {![]()
![]()
![]()
![]()
![]() 7
7![]()
![]() 73
73![]()
![]()
![]()
![]() } -
иррациональные числа
} -
иррациональные числа
Замечание. Любое иррациональное число - бесконечная непериодическая десятичная дробь.
Действительные числа.
объединение рациональных и иррациональных чисел называют
действительными числами. Множество действительных чисел обозначают
символом R.R![]() Q
Q![]() Z
Z![]() N
N
Замечание. Любое действительное число - бесконечная десятичная дробь.
Множества
Натуральных чисел: ![]()
Целых чисел: ![]()
Рациональных чисел: 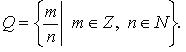
Действительных(вещественных) чисел:
![]()
Числовые промежутки
Отрезок (замкнутый промежуток, сегмент):
![]()
Интервал (открытый промежуток):
![]()
Полуинтервалы:
![]()
![]()
Бесконечные числовые промежутки (лучи, полупрямые):
![]()
![]()
Числовая прямая: ![]()
Замечание. Наряду с приведенными
используются и обозначения ![]() -
для интервала;
-
для интервала; ![]() -
для полуинтервалов;
-
для полуинтервалов; ![]()
![]()
![]()
![]() -
для лучей;
-
для лучей; ![]() -
для числовой прямой.
-
для числовой прямой.
Метод математической индукции
Метод математической индукции является важным способом доказательства предложений (утверждений), зависящих от натурального аргумента.
Метод математической индукции состоит в следующем:
Предложение (утверждение) P(n), зависящее от натурального числа n, справедливо для любого натурального n если:
-
P(1) является истинным предложением (утверждением);
-
P(n) остается истинным предложением (утверждением), если n увеличить на единицу, то есть P(n + 1) - истинное предложение (утверждение).
Таким образом метод математической индукции предполагает два этапа:
-
Этап проверки: проверяется, истинно ли предложение (утверждение) P(1).
-
Этап доказательства: предполагается, что предложение P(n) истинно, и доказывается истинность предложения P(n + 1) (n увеличено на единицу).
Замечание 1. В некоторых случаях метод математической индукции используется в следующей форме:
Пусть m - натуральное число, m > 1 и P(n) - предложение, зависящее от n, n ≥ m.
Если
-
P(m) справедливо;
-
P(n) будучи истинным предложением, влечет истинность предложения P(n + 1) для любого натурального n, n ≥ m, тогда P(n) - истинное предложение для любого натурального n, n ≥ m.
В дальнейшем рассмотрим примеры применения метода математической индукции.
Пример 1. Доказать следующие равенства
Решение. a) При n = 1 равенство примет вид
![]() 1=1, следовательно, P(1) истинно. Предположим, что данное равенство
справедливо, то есть, имеет место
1=1, следовательно, P(1) истинно. Предположим, что данное равенство
справедливо, то есть, имеет место
![]() .
.
Следует проверить (доказать), что P(n + 1), то есть
![]()
истинно. Поскольку (используется предположение индукции)
![]()
получим
![]()
то есть, P(n + 1) - истинное утверждение.
Таким образом, согласно методу математической индукции, исходное равенство справедливо для любого натурального n.
c) При n = 1 равенство истинно: ![]() 1=1. Допустим, что истинно равенство
1=1. Допустим, что истинно равенство
![]() и
покажем, что
и
покажем, что
![]()
то есть истинность P(n) влечет истинность P(n + 1). Действительно,
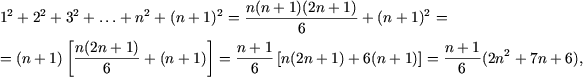
и, так как 2n2 + 7n + 6 = (2n + 3)(n + 2), получим
![]()
и, следовательно, исходное равенство справедливо для любого натурального n.
d) При n = 1 равенство справедливо: ![]() 1=1. Допустим, что имеет место
1=1. Допустим, что имеет место
![]()
и докажем, что
![]()
Действительно,
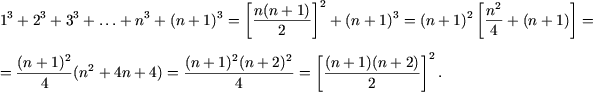
e) Утверждение P(1) справедливо: ![]() 2=2. Допустим, что равенство
2=2. Допустим, что равенство
![]()
справедливо, и докажем, что оно влечет равенство
![]()
Действительно,
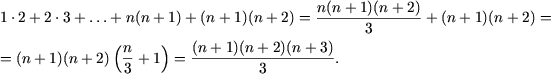
Следовательно, исходное равенство имеет место для любого натурального n.
f) P(1) справедливо: ![]() 1/3 = 1/3. Пусть имеет
место равенство P(n):
1/3 = 1/3. Пусть имеет
место равенство P(n):
![]() .
.
Покажем, что последнее равенство влечет следующее:
![]()
Действительно, учитывая, что P(n) имеет место, получим
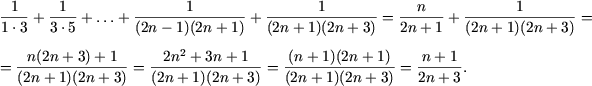
Таким образом, равенство доказано.
Действия над действительными числами
Свойства сложения:
a + b = b + a - переместительное свойство
(a + b) +c = a + (b + c) - сочетательное свойство
a + 0 = a - свойство нуля
a + (-a) = 0 - сумма противоположных чисел
Свойства вычитания:
a - (b + c) = a - b - c вычитание суммы чисел от числа
(a + b) - c = (a - c) + b = a + (b - c) - вычитание числа от суммы
a - 0 = a - свойство нуля
0 - a = -a - свойство нуля
Свойства умножения:
a· b = b· a - переместительное свойство
(a · b)· c = a· (b · c) -сочетательное свойство
(a - b)· c = a · c - b · c - распределительное свойство
(a + b)· c = a · c + b · c - распределительное свойство
a · 1 = a - свойство единицы
a · 0 = 0 - свойство нуля
a![]() a1=1
a1=1![]() a
a![]() =0 -
свойство обратных чисел
=0 -
свойство обратных чисел
Свойства деления:
(a · b) : c = a · (b : c) = (a : c) · b - деления произведения на число
(a + b) : c = a : c + b : c - деление суммы на число
(a - b) : c = a : c - b : c - деление разности на число
a : (b ·c) = (a: b) :c = (a : c) : b - деление числа на произведение
a : 1 = a; 0 : a = 0 ;
a : a = 1, a![]() =0-
свойство единицы и нуля
=0-
свойство единицы и нуля
Определение: Выражение вида
b/a или a : b, где а и
b целые числа, b![]() 0
, называется дробью
0
, называется дробью
-
Число a называется числителем дроби. Число b называется знаменателем дроби
-
Если a < b, то выражение ba правильная дробь
-
Если a > b , то выражение ba неправильная дробь. Из любой неправильной дроби можно выделить целую часть и дробную часть. Примеры: 67=161, 518=353
Основное свойство дроби: Две
дроби ba и cd называются равными если
a![]() d=b
d=b![]() c
.
c
.
Действия над дробями (ba и cd):
-
ba=b
 ka
ka k
- Дробь не изменится, если числитель и знаменатель дроби
умножить на одно и то же число
k
- Дробь не изменится, если числитель и знаменатель дроби
умножить на одно и то же число
-
Если b = d, то ba
 cd=ba
cd=ba c
c
-
Если b
 =d
, то дроби нужно привести к общему знаменателю:
ba
=d
, то дроби нужно привести к общему знаменателю:
ba cd=bdad
cd=bdad cb.
Общим знаменателем будет НОК (b, d)
cb.
Общим знаменателем будет НОК (b, d)
-
Если k целое число, то k
 ba=bk
ba=bk a
или ba:k=ab
a
или ba:k=ab k
k
-
Две дроби можно умножать ba
 cd=a
cd=a cb
cb d
или делить ba:cd=b
d
или делить ba:cd=b ca
ca d
d
Сложение и вычитание десятичных дробей. Эти операции выполняются так же, как и сложение и вычитание целых чисел. Необходимо только записать соответствующие десятичные знаки один под другим.
П р и м е р .
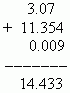
Умножение десятичных дробей. На первом этапе перемножаем десятичные дроби как целые числа, не принимая во внимание десятичную точку. Затем применяется следующее правило: количество десятичных знаков в произведении равно сумме десятичных знаков во всех сомножителях.
Замечание: до простановки десятичной точки в произведении нельзя отбрасывать нули в конце!
П р и м е р .

Сумма чисел десятичных знаков в сомножителях равна: 3 + 4 = 7. Сумма цифр в произведении равна 6. Поэтому необходимо добавить один ноль слева: 0197056 и проставить перед ним десятичную точку: 0.0197056.
Деление десятичных дробей
Если делимое меньше делителя, записываем ноль в целой части частного и ставим после него десятичную точку. Затем, не принимая во внимание десятичную точку делимого, присоединяем к его целой части следующую цифру дробной части и опять сравниваем полученную целую часть делимого с делителем. Если новое число опять меньше делителя, ставим ещё один ноль после десятичной точки в частном и присоединяем к целой части делимого следующую цифру его дробной части. Этот процесс повторяем до тех пор, пока полученное делимое не станет больше делителя. После этого деление выполняется, как для целых чисел. Если делимое больше делителя или равно ему, сначала делим его целую часть, записываем результат деления в частном и ставим десятичную точку. После этого деление продолжается, как в случае целых чисел.
П р и м е р . Разделить 1.328 на 64.
Р е ш е н и е : 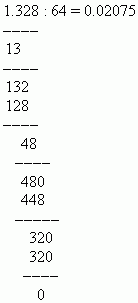
I. Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить тот же.
Примеры.
![]()
II. Если нужно сложить дроби с разными знаменателями, то сначала дроби приводят к наименьшему общему знаменателю, а затем складывают дроби с одинаковыми знаменателями.
Примеры.

III. Чтобы выполнить вычитание дробей с одинаковыми знаменателями, из числителя первой дроби вычитают числитель второй дроби, а знаменатель оставляют тот же.
Примеры.
![]()
IV. Если нужно выполнить вычитание дробей с разными знаменателями, то их сначала приводят к общему знаменателю, а затем выполняют вычитание дробей с одинаковыми знаменателями.
Примеры.
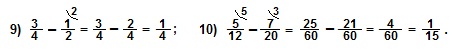
V. При выполнении действий сложения или вычитания смешанных чисел эти действия выполняют отдельно для целых частей и для дробных частей, а затем результат записывают в виде смешанного числа.
Примеры.
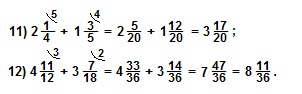 Да,
складывать нужно отдельно целые части и отдельно дробные части
смешанного числа.
Да,
складывать нужно отдельно целые части и отдельно дробные части
смешанного числа.
Нет, не нужно расписывать целые и дробные части смешанных чисел по отдельности.
Важно: не начинайте выполнять сложение, пока не приведете дробные части данных смешанных чисел к наименьшему общему знаменателю (НОЗ).
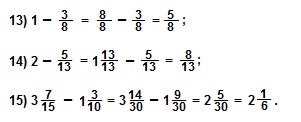 Помним,
что единицу можно представить в виде обыкновенной дроби, числитель
и знаменатель которой, являются любыми равными друг другу числами.
Помним,
что единицу можно представить в виде обыкновенной дроби, числитель
и знаменатель которой, являются любыми равными друг другу числами.
Важно: не начинайте выполнять вычитание, пока не приведете дробные части данных смешанных чисел к наименьшему общему знаменателю (НОЗ) и не убедитесь, что из числителя первой дроби можно вычесть числитель второй дроби. А если нельзя вычесть?
Тогда «занимаете» у целой части уменьшаемого одну целую единицу, представляете ее в виде неправильной дроби с таким же знаменателем (НОЗ), и добавляете эту неправильную дробь (раздробленную единицу) к дробной части уменьшаемого.
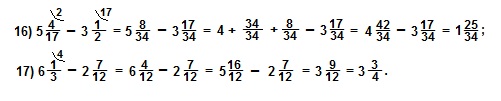
Модуль числа и числовая прямая
Модуль действительного числа - это абсолютная величина этого числа.
Попросту говоря, при взятии модуля нужно отбросить от числа его знак.
Модуль числа a обозначается |a|. Обратите внимание: модуль числа всегда неотрицателен: |a|≥ 0.
|6| = 6, |-3| = 3, |-10,45| = 10,45
Определение модуля
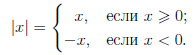
Свойства модуля
1. Модули противоположных чисел равны![]()
2. Квадрат модуля числа равен квадрату этого числа
![]()
3. Квадратный корень из квадрата числа есть модуль этого числа
![]()
![]()
4. Модуль числа есть число неотрицательное
![]()
5. Постоянный положительный множитель можно выносить за знак модуля
![]() ,
,
![]()
6. Если ![]() , то
, то
![]()
7. Модуль произведения двух (и более) чисел равен произведению их модулей
![]()
8.
Геометрический смысл модуля
Модуль числа - это расстояние от нуля до данного числа.
Например, |-5| = 5. То есть расстояние от точки -5 до нуля равно 5.

Рассмотрим простейшее уравнение |x| = 3. Мы видим, что на числовой прямой есть две точки, расстояние от которых до нуля равно трём. Это точки 3 и -3. Значит, у уравнения |x| = 3 есть два решения: x = 3 и x = -3.
Пример 1.
|x - 3| = 4.
Это уравнение можно прочитать так: расстояние от
точки ![]() до
точки
до
точки ![]() равно
равно ![]() . С
помощью графического метода можно определить, что уравнение имеет
два решения:
. С
помощью графического метода можно определить, что уравнение имеет
два решения: ![]() и
и
![]() .
.
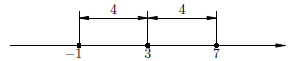
Пример 2.
Решим неравенство: |x + 7| < 4.
Можно прочитать как: расстояние от точки
![]() до
точки
до
точки ![]() меньше четырёх. Ответ: (-11; -3).
меньше четырёх. Ответ: (-11; -3).
![]()
Пример 3.
Решим неравенство: |10 - x| ≥ 7.
Расстояние от точки 10 до точки ![]() больше или равно семи. Ответ: (-∞; 3]υ [17, +∞)
больше или равно семи. Ответ: (-∞; 3]υ [17, +∞)
![]()
Отношения. Пропорция. Процент
Отношение - это частное от деления одного числа на другое.
Пропорция - это равенство двух отношений. Например,
12 : 20 = 3 : 5; a : b = c : d .
Крайние члены пропорции: 12 и 5 в первой пропорции; a и d - во второй.
Средние члены пропорции: 20 и 3 в первой пропорции; b и с - во второй.
Основное свойство пропорции: Произведение крайних членов пропорции равно произведению её средних членов.
Две взаимно зависимых величины называются пропорциональными, если отношение их величин сохраняется неизменным.
Это постоянное отношение пропорциональных величин называется коэффициентом пропорциональности. П р и м е р .
Масса любого вещества пропорциональна его объёму. Например, 2 литра ртути весят 27.2 кг, 5 литров весят 68 кг, 7 литров весят 95.2 кг. Отношение массы ртути к её объёму ( коэффициент пропорциональности )будет равно:
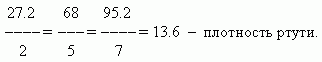
Таким образом, коэффициентом пропорциональности в данном примере
является плотность.
Процент
Процентом называется сотая часть от числа, т.е. 1%А = 0,01А
1% = 0,01, 2% = 0,02, 45% = 0,45, 350% = 3,5. Часто встречающиеся проценты: 5% = 0,05 = 120, 10% = 0,1 = 110, 20% = 0,2 = 51, 25% = 0,25 = 41, 50% = 0,5 = 21, 75% = 0,75 =43
Основные типы задач.
-
Сколько процентов составляет число А от числа В?
Решение: x=ВА![]() 100%
100%
-
Число А увеличилось на 20%, а затем полученное число уменьшилось на 25%. Как, в итоге, изменилось исходное число?
Решение: 1) А1= (100% + 20%)А = 120%А = 1,2А 2) А2= (100% - 25%)А1 = 75%А1 = 0,75А1 = 0,75 1,2А = 0,9А = 90%А 3) А2 - А = 90%А - 100%А = -10%. Ответ: число уменьшилось на 10%.
-
Как изменится время, если скорость движения увеличится на 25%?
Решение: 1)t=SV
2) t1=SV1=S1![]() 25V=11
25V=11![]() 25SV=0
25SV=0![]() 8SV=80%t.
Ответ: уменьшится на 20%.
8SV=80%t.
Ответ: уменьшится на 20%.
 Основные
задачи на проценты
Основные
задачи на проценты
Замечание. Для того чтобы записать проценты десятичной дробью или натуральным числом, нужно число, которое стоит перед знаком %, разделить на 100.
Например: 1) 24% = 24 : 100 = 0,24 ; 2) 700% = 700 : 100 = 7
Основные типы задач на проценты.
Задача 1. Нахождение процента p% от числа b
Если число a составляет
p% от числа b, то эти числа
связаны равенством 100%![]() a=p%
a=p%![]() b
или b100=pa или a=b
b
или b100=pa или a=b![]() p100
p100
Задача 2. Нахождение числа a по данному проценту p%
Если p% какого нубудь числа a равно b, то эти числа связаны равенством a=b:p100=p100b
Задача 3. Нахождение прцентного отношения чисел a и b
Число a составляет
ba![]() 100%
от числа b
100%
от числа b
Задача 4. Увеличения на p%
Если число a увеличено на
p%, то оно увеличено в
![]() 1+p100
1+p100![]() раз, то получится число a
раз, то получится число a![]()
![]() 1+p100
1+p100![]() .
.
Задача 5. Уменьшение на q%
Если уменьшено на
q%, 0![]() q
q![]() 100
, то оно уменьшено в
100
, то оно уменьшено в ![]() 1−p100
1−p100![]() раз, то получаются число a
раз, то получаются число a![]()
![]() 1−p100
1−p100![]()
Задача 6. Начисление простых процентов
При многократном начислении простых
процентов начисление делается по отношению к исходной сумме и
представляет собой каждый раз одну и ту же величину:
S=a![]()
![]() 1+n
1+n![]() p100
p100![]() ,
где a - исходная сумма, S -
наращенная сумма, p% - процентная ставка,
n - число периодов начисления.
,
где a - исходная сумма, S -
наращенная сумма, p% - процентная ставка,
n - число периодов начисления.
.Задача 7. Начисление сложных процентов
При многократном начислении сложных
процентов начисление каждый раз делается по отношению к сумме
с уже начисленными ранее процентами: S=a![]()
![]() 1+p100
1+p100![]() n
, где a - исходная сумма, S -
наращенная сумма, p% - процентная ставка,
n - число периодов начисления.
n
, где a - исходная сумма, S -
наращенная сумма, p% - процентная ставка,
n - число периодов начисления.
2.ФУНКЦИИ
Определения, виды и свойства функций
Функцией 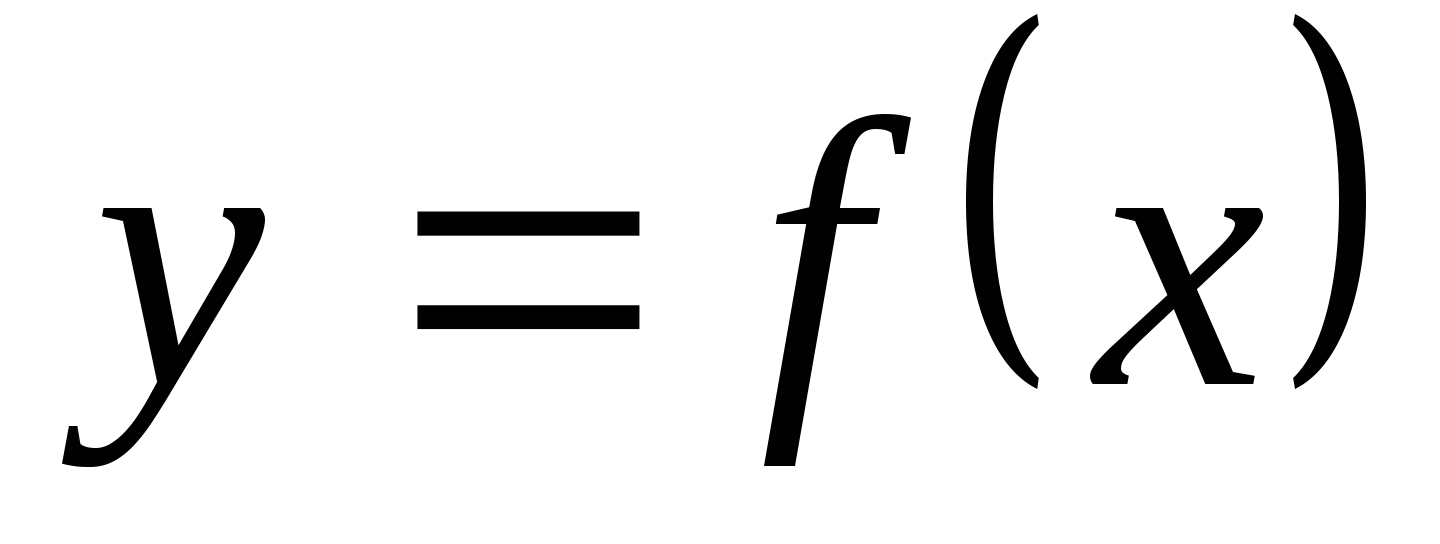 называется соответствие между множествами
называется соответствие между множествами 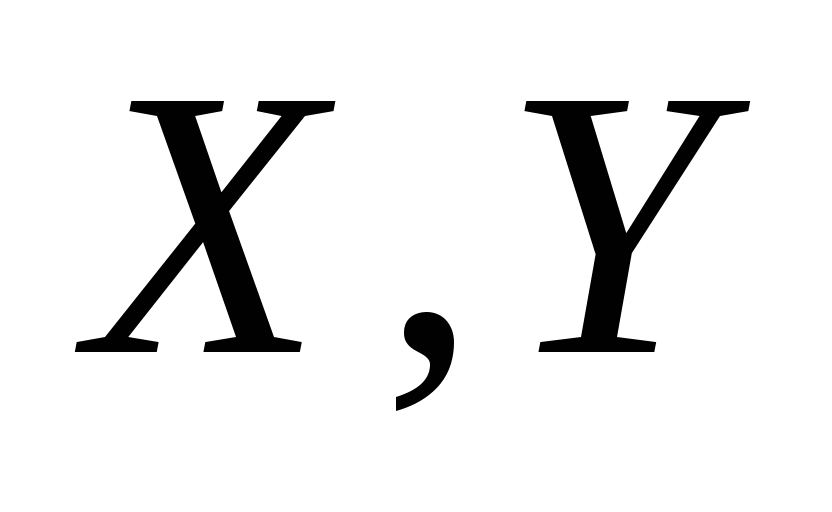 ,
кога каждому значению
,
кога каждому значению 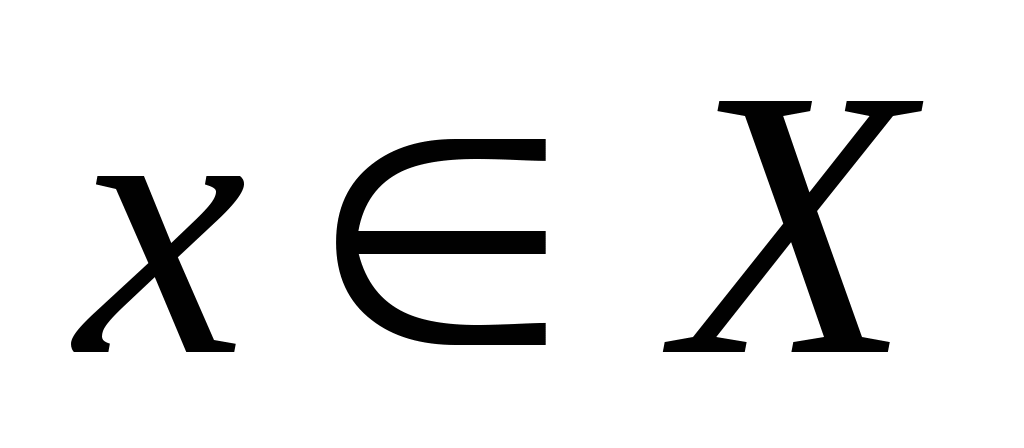 соответствует неболее один
соответствует неболее один 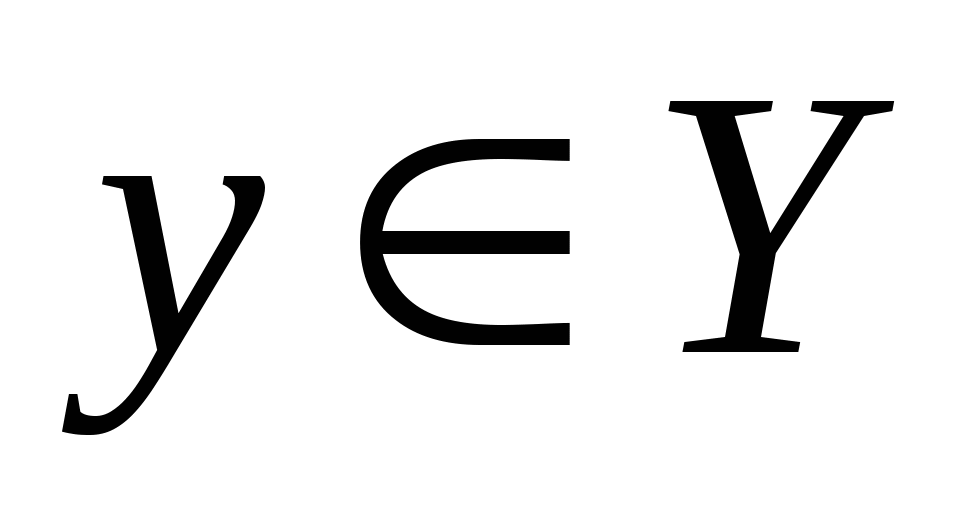 .
.
Основные элементарные функции:
-
степенная
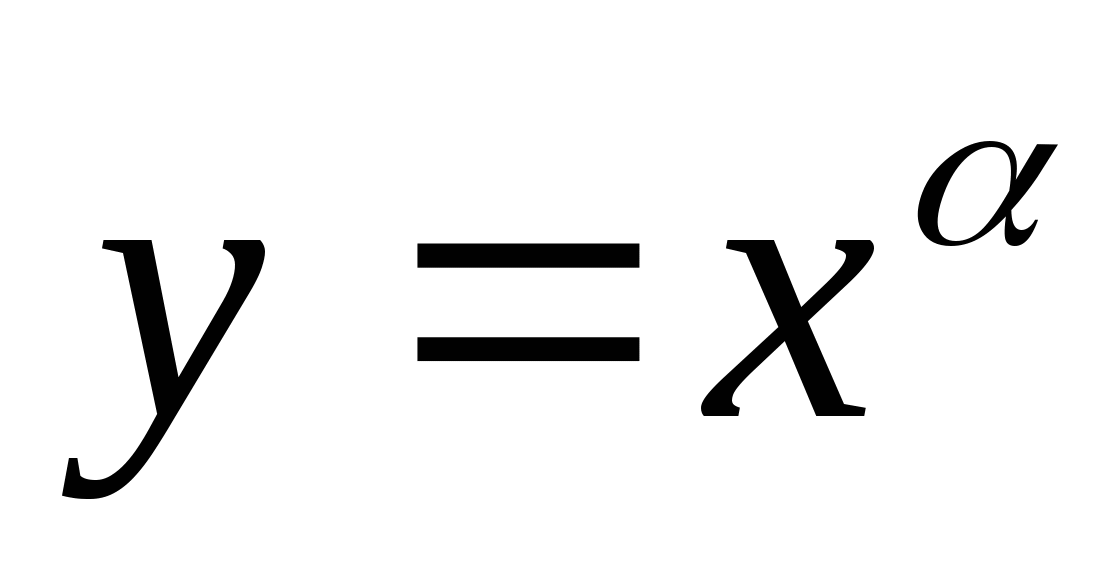 ;
;
-
показательная
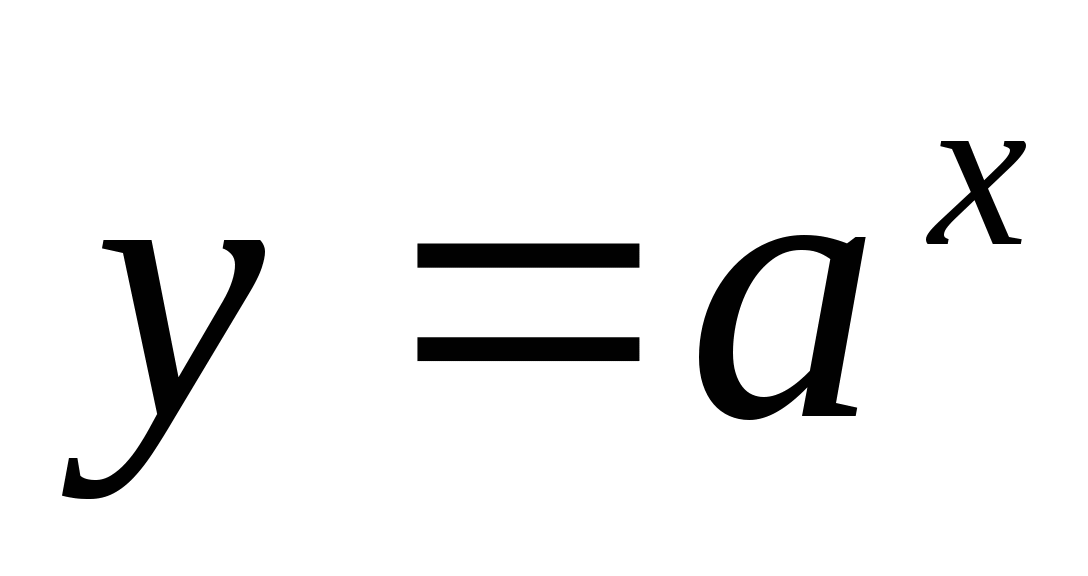 ;
;
-
логарифмическая
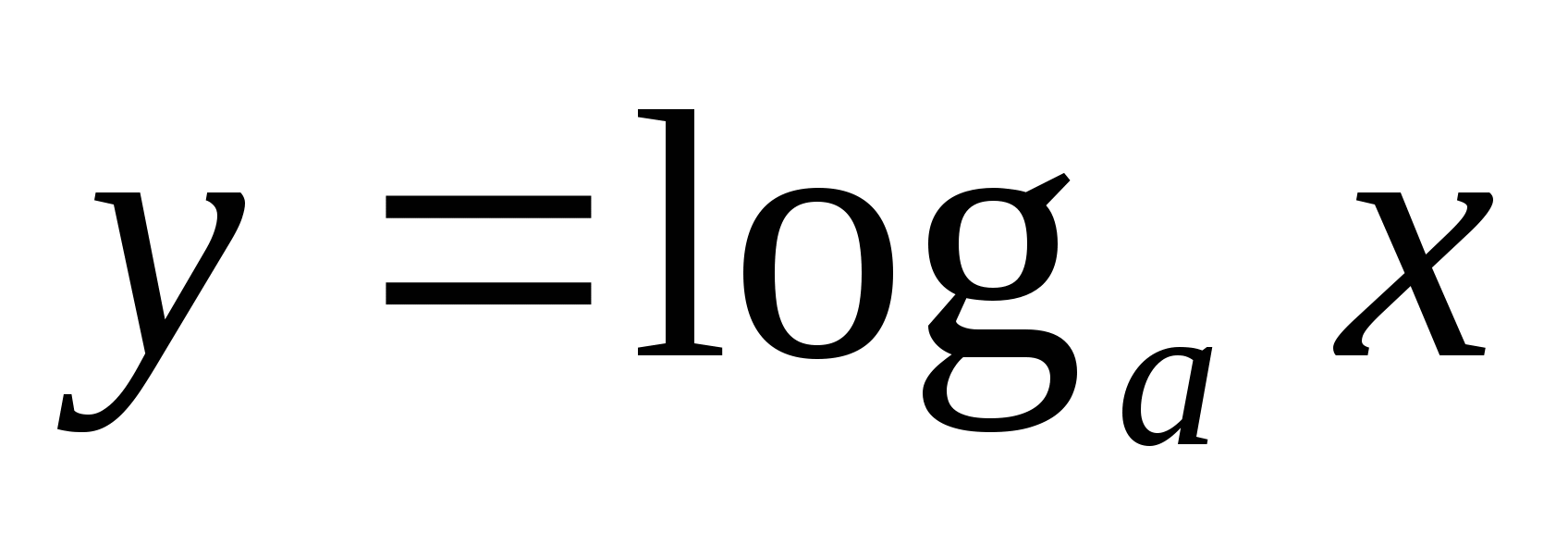 ;
;
-
тригонометрические
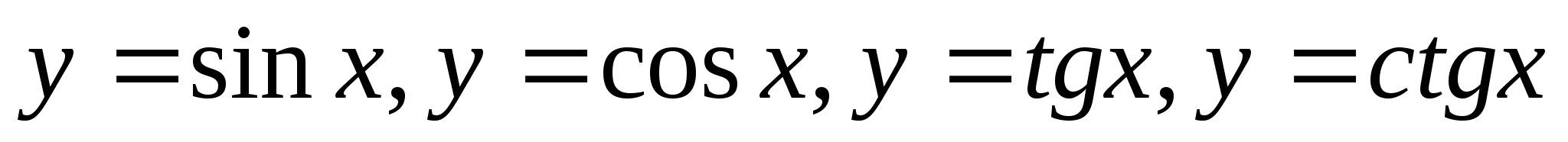 ;
;
-
обратные тригонометрическим
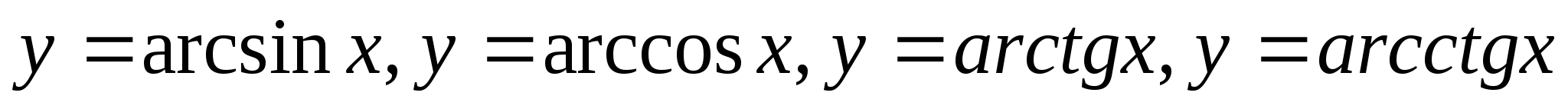
(Смотри видеоурок 1, 2, 5, 9)
Пример1. Найти область определения
функции ![]()
Решение.
Так как функция представляет собой сумму
функций, то область определения функции будет состоять из всех тех
значений х, которые принадлежат одновременно области определения
функций ![]() и
и
![]() .
Поэтому область определения заданной функции определяется как
совокупность значений х,при которых одновременно выполняются
неравенства
.
Поэтому область определения заданной функции определяется как
совокупность значений х,при которых одновременно выполняются
неравенства ![]() Это будет интервал (1,2).
Это будет интервал (1,2).
Пример2. Доказать, что функция ![]() -
нечетная.
-
нечетная.
Решение.
Область определения функции: ![]()
Следовательно, функция нечетная.
Построение графиков элементарных функций
Графики элементарных функций
Данный методический материал носит справочный характер и относится к широкому кругу тем. В статье приведен обзор графиков основных элементарных функций и рассмотрен важнейший вопрос - как правильно и БЫСТРО построить график. В ходе изучения высшей математики без знания графиков основных элементарных функций придётся тяжело, поэтому очень важно вспомнить, как выглядят графики параболы, гиперболы, синуса, косинуса и т.д., запомнить некоторые значения функций. Также речь пойдет о некоторых свойствах основных функций.
Я не претендую на полноту и научную основательность материалов, упор будет сделан, прежде всего, на практике - тех вещах, с которыми приходится сталкиваться буквально на каждом шагу, в любой теме высшей математики.
Как правильно построить координатные оси?
На практике контрольные работы почти всегда оформляются студентами в отдельных тетрадях, разлинованных в клетку. Зачем нужна клетчатая разметка? Ведь работу, в принципе, можно сделать и на листах А4. А клетка необходима как раз для качественного и точного оформления чертежей.
Любой чертеж графика функции начинается с координатных осей.
Чертежи бывают двухмерными и трехмерными.
Сначала рассмотрим двухмерный случай декартовой прямоугольной системы координат:
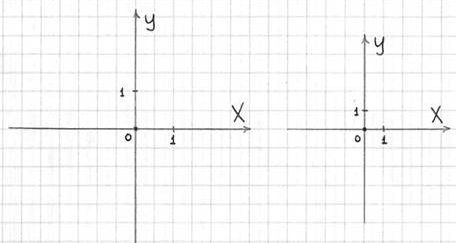
1) Чертим координатные оси. Ось ![]() называется осью абсцисс, а ось
называется осью абсцисс, а ось ![]() -
осью ординат. Чертить их всегда стараемся
аккуратно и не криво. Стрелочки тоже не должны
напоминать бороду Папы Карло.
-
осью ординат. Чертить их всегда стараемся
аккуратно и не криво. Стрелочки тоже не должны
напоминать бороду Папы Карло.
2) Подписываем оси большими буквами «икс» и «игрек». Не забываем подписывать оси.
3) Задаем размерность по осям: рисуем
ноль и две единички. При выполнении чертежа самая удобная
и часто встречающаяся размерность: 1 единица = 2 клеточки (чертеж
слева). Я рекомендую Вам по возможности всегда придерживаться
именно такой размерности. Но, время от времени случается так, что
чертеж не вмещается на тетрадный лист - тогда размерность
уменьшаем: 1 единица = 1 клеточка (чертеж справа).
Редко-редко, но бывает, что размерность чертежа приходиться
уменьшать (или увеличивать) еще больше.
НЕ НУЖНО по осям проставлять все значения: …-5, -4, -3, -1, 0, 1, 2, 3, 4, 5, …. Ибо координатная плоскость - не памятник Лобачевскому, а студент - не голубь. Ставим ноль и две единицы по осям. Как говорят математики, это необходимо и достаточно. Размерность можно задать и произвольно, например, поставить 0 и - 1, -1 - по осям, но существуют некоторые стандарты, которых целесообразно придерживаться.
График линейной функции
Линейная функция задается уравнением ![]() .
График линейной функций представляет собой прямую.
Для того, чтобы построить прямую достаточно знать две точки.
.
График линейной функций представляет собой прямую.
Для того, чтобы построить прямую достаточно знать две точки.

1) Линейная функция вида ![]() (
(![]() )
называется прямой пропорциональностью. Например,
)
называется прямой пропорциональностью. Например, ![]() .
График прямой пропорциональности всегда проходит через начало
координат. Таким образом, построение прямой упрощается - достаточно
найти всего одну точку.
.
График прямой пропорциональности всегда проходит через начало
координат. Таким образом, построение прямой упрощается - достаточно
найти всего одну точку.
2) Уравнение вида ![]() задает прямую, параллельную оси
задает прямую, параллельную оси ![]() , в
частности, сама ось
, в
частности, сама ось ![]() задается уравнением
задается уравнением ![]() .
График функции строится сразу, без нахождения всяких точек. То
есть, запись
.
График функции строится сразу, без нахождения всяких точек. То
есть, запись ![]() следует понимать так: «игрек всегда равен -4, при любом значении
икс».
следует понимать так: «игрек всегда равен -4, при любом значении
икс».
3) Уравнение вида ![]() задает прямую, параллельную оси
задает прямую, параллельную оси ![]() , в
частности, сама ось
, в
частности, сама ось ![]() задается уравнением
задается уравнением ![]() .
График функции также строится сразу. Запись
.
График функции также строится сразу. Запись ![]() следует понимать так: «икс всегда, при любом значении игрек, равен
1».
следует понимать так: «икс всегда, при любом значении игрек, равен
1».
Некоторые спросят, ну зачем вспоминать 6 класс?!
Так-то оно, может и так, только за годы практики я встретил добрый
десяток студентов, которых ставила в тупик задача построения
графика вроде ![]() или
или
![]() .
.
Построение прямой - самое распространенное действие при выполнении чертежей.
Прямая линия детально рассматривается в курсе аналитической геометрии, и желающие могут обратиться к статье Уравнение прямой на плоскости.
График квадратичной, кубической функции, график многочлена
Парабола. График квадратичной функции ![]() (
(![]() )
представляет собой параболу. Рассмотрим знаменитый случай:
)
представляет собой параболу. Рассмотрим знаменитый случай:
![]()

кубическая парабола
Кубическая парабола задается функцией ![]() .
Вот знакомый со школы чертеж:
.
Вот знакомый со школы чертеж:
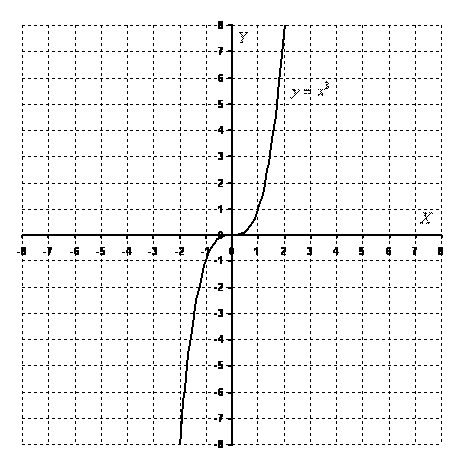
График функции ![]()
Он представляет собой одну из ветвей параболы</</u>. Выполним чертеж:

График гиперболы
Опять же вспоминаем тривиальную «школьную»
гиперболу ![]() .
.

График показательной функции
В данном параграфе я сразу рассмотрю
экспоненциальную функцию ![]() ,
поскольку в задачах высшей математики в 95% случаев встречается
именно экспонента.
,
поскольку в задачах высшей математики в 95% случаев встречается
именно экспонента.
Напоминаю, что ![]() -
это иррациональное число:
-
это иррациональное число: ![]() ,
это потребуется при построении графика, который, собственно, я без
церемоний и построю. Трёх точек, пожалуй, хватит:
,
это потребуется при построении графика, который, собственно, я без
церемоний и построю. Трёх точек, пожалуй, хватит:
![]()
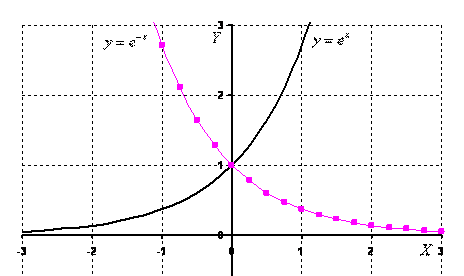
График логарифмической функции
Рассмотрим функцию с натуральным логарифмом
![]() .
.
Выполним поточечный чертеж:
![]()

Графики тригонометрических функций
Построим график функции ![]()

График косинуса
Построим график функции ![]()

Графики тангенса
Построим график функции ![]()

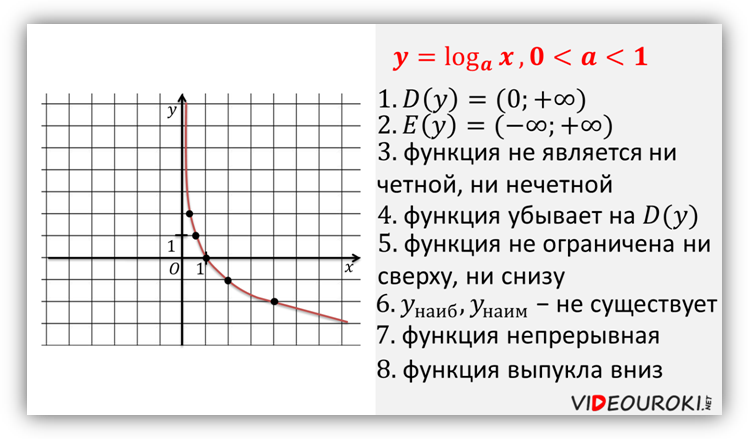
График показательной функции при ![]()
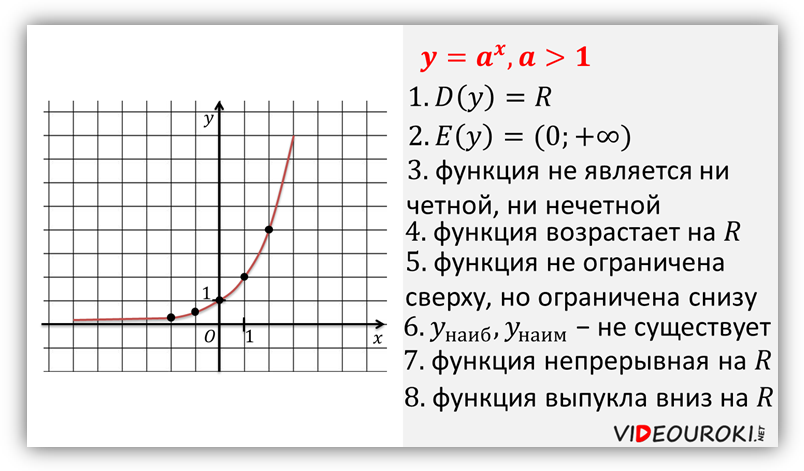
График показательной функции при ![]()
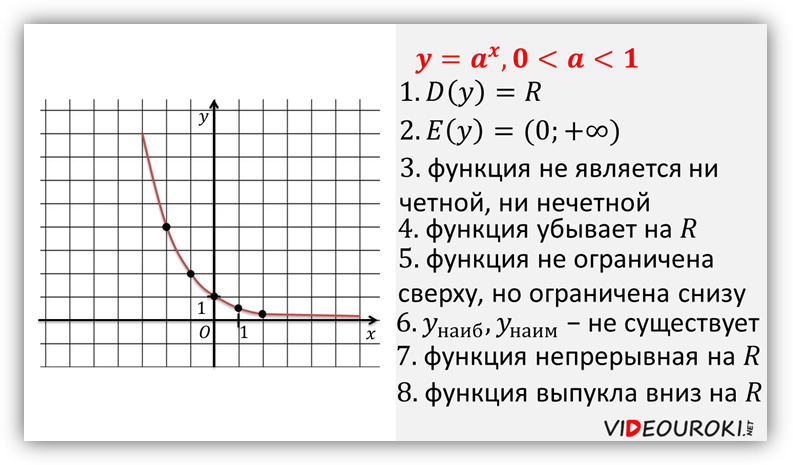
График логарифмической функции при ![]()
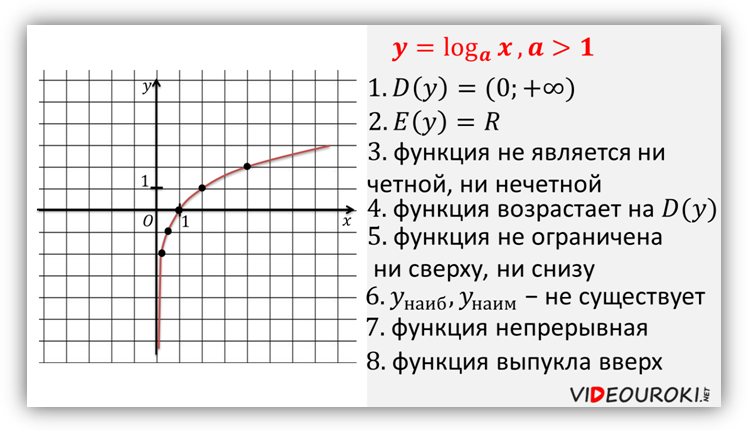
График логарифмической функции при ![]()
Тригонометрия
Основные тригонометрические формулы
Формула
Допустимые значения аргумента
1.1
![]()
![]()
1.2
![]()
![]()
1.3
![]()
![]()
1.4
![]()
![]()
Решение простых тригонометрических уравнений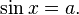
Если ![]() -
вещественных решений нет.
-
вещественных решений нет.
Если ![]() -
решением является число вида
-
решением является число вида ![]()
Если ![]() -
вещественных решений нет.
-
вещественных решений нет.
Если ![]() -
решением является число вида
-
решением является число вида ![]()
Решением является число вида ![]()
Решением является число вида ![]()
(Смотри видеоуроки 3, 4, 7, 10, 12, 14, 16, 17).
3. ПРОИЗВОДНАЯ И ИНТЕГРАЛ
Предел функции
Число А называется пределом функции
![]() в
точке
в
точке ![]() ,
если для любого
,
если для любого ![]() существует
существует ![]() такое, что для всех
такое, что для всех ![]() ,
удовлетворяющих неравенству
,
удовлетворяющих неравенству ![]() ,
выполняется неравенство
,
выполняется неравенство ![]()
Записывают ![]()
Функция ![]() называется непрерывной в точке
называется непрерывной в точке ![]() ,
если предел функции и ее значение в этой точке равны,
,
если предел функции и ее значение в этой точке равны, ![]()
Первый замечательный предел ![]() .
.
Второй замечательный предел ![]()
Правило Лопиталя: если ![]()
Пример 1. Найти ![]()
Решение. ![]()
Пример 2. Вычислить ![]()
Решение. Заменяя каждый из многочленов
своим старшим членом, имеем: ![]()
Пример 3. Найти ![]()
Решение.
Имеем неопределенность вида ![]() Применяя правило Лопиталя, получаем
Применяя правило Лопиталя, получаем
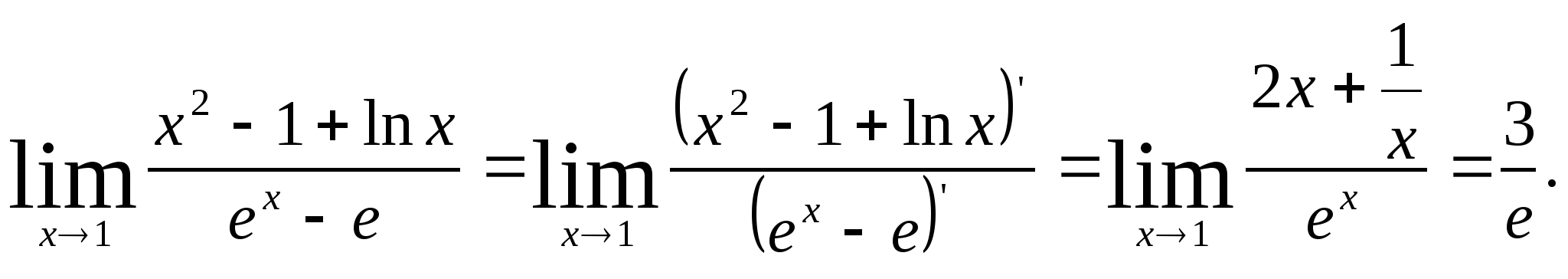
Пример 4. .Вычислить предел ![]()
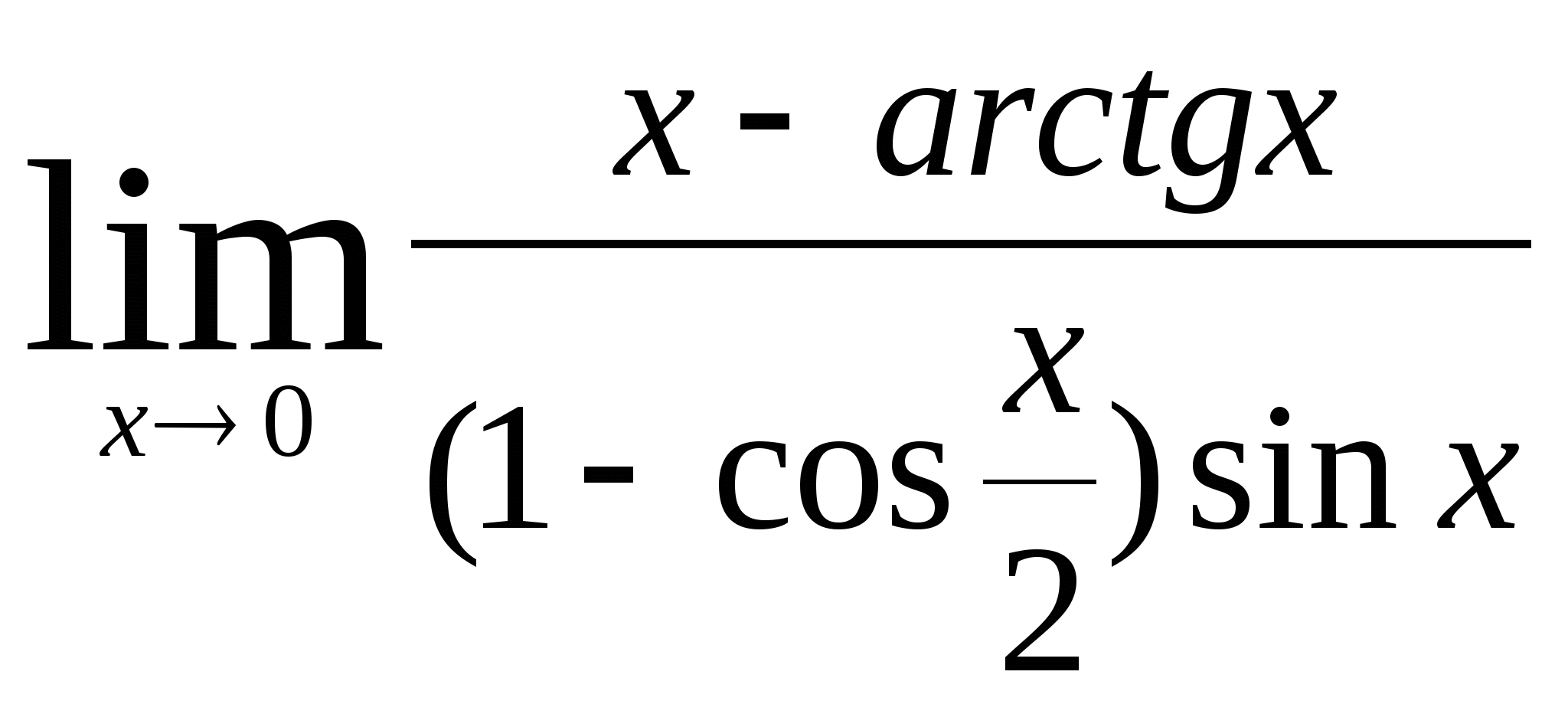
Решение.
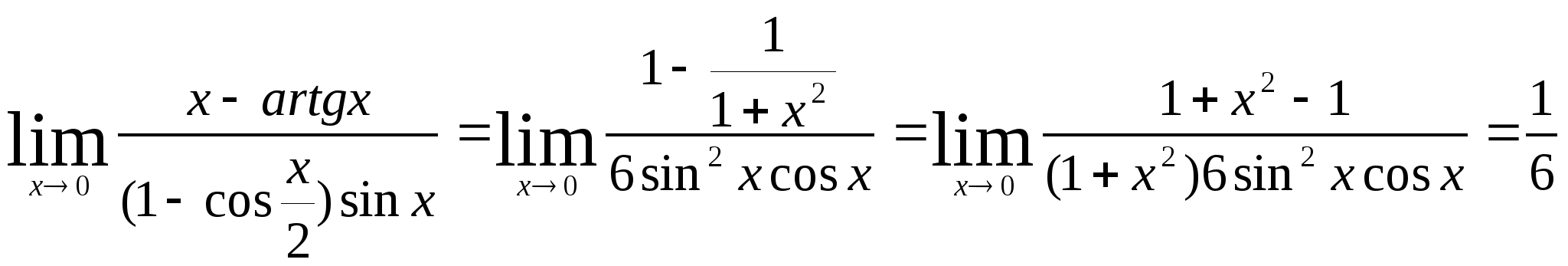 Ответ:
Ответ:![]()
Пример 5. Найти асимптоты функции
![]()
Решение.
![]() -вертикальные
асимптоты.
-вертикальные
асимптоты.
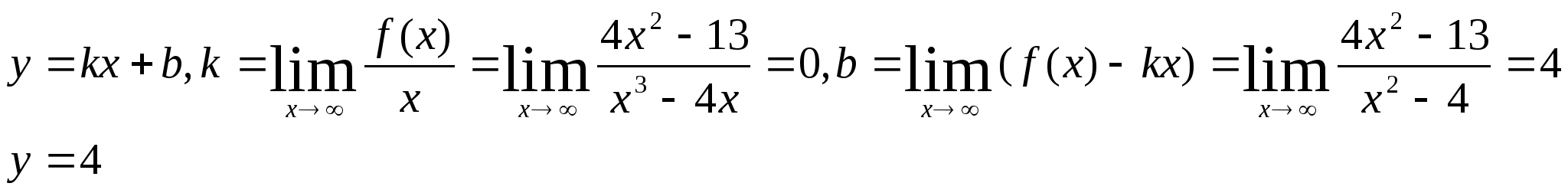 ,
,
Ответ:![]() -асимптоты.
-асимптоты.
Дифференцирование функции одной переменной
Определение. Производной функции
![]() в
точке
в
точке ![]() называется предел отношения приращения функции к приращению
аргумента, когда последний стремится к нулю.
называется предел отношения приращения функции к приращению
аргумента, когда последний стремится к нулю.
Обозначают ![]()
Правила вычисления производных
1. ![]() , 2.
, 2.
![]() , 3.
, 3.
![]()
Таблица производных
1.![]()
2.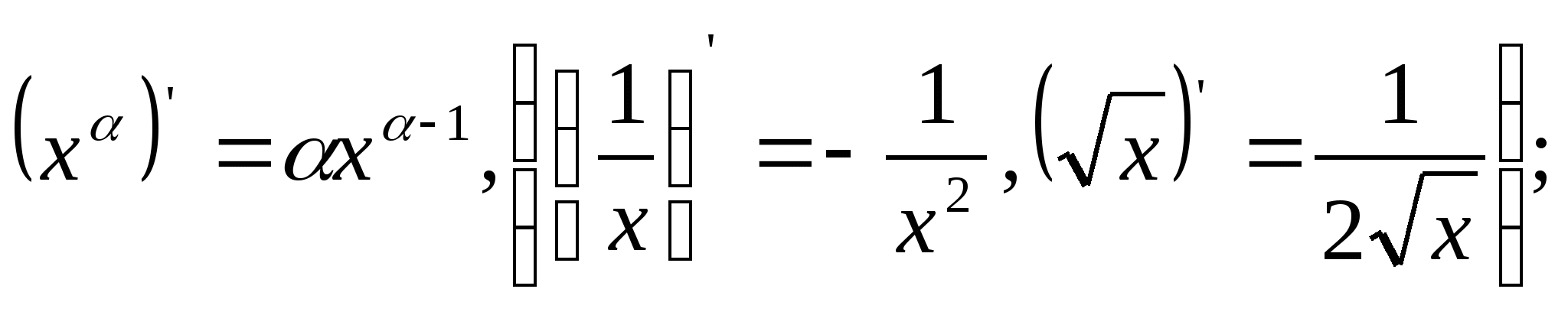
3.![]()
4.![]()
5.![]()
6.![]()
7.![]()
8.![]()
9.![]()
10.![]()
Пример 1. Используя правила и формулы
дифференцирования найти производные функций: 1)![]()
2) ![]() 3)
3)
![]() 4)
4)
![]()
Решение.
1) ![]()
2) 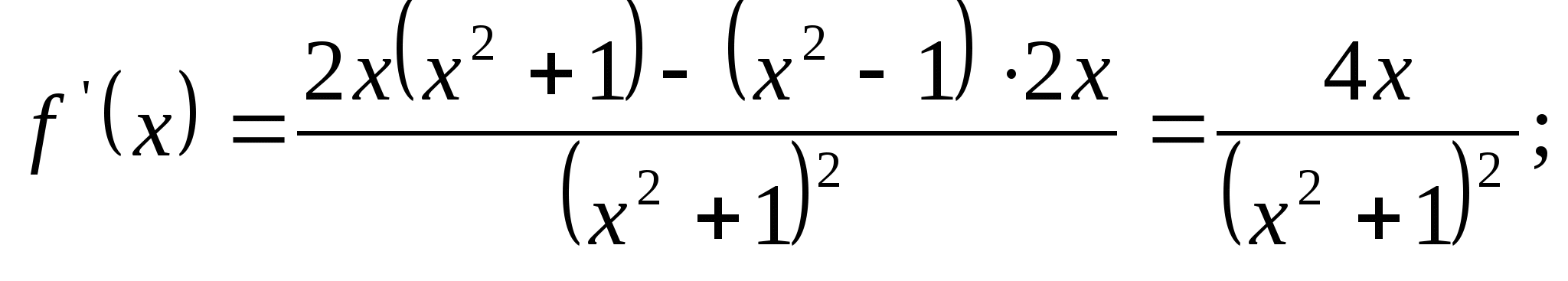
3) ![]()
4) ![]()
Пример 2. Определить глобальные
экстремумы ![]()
Решение.
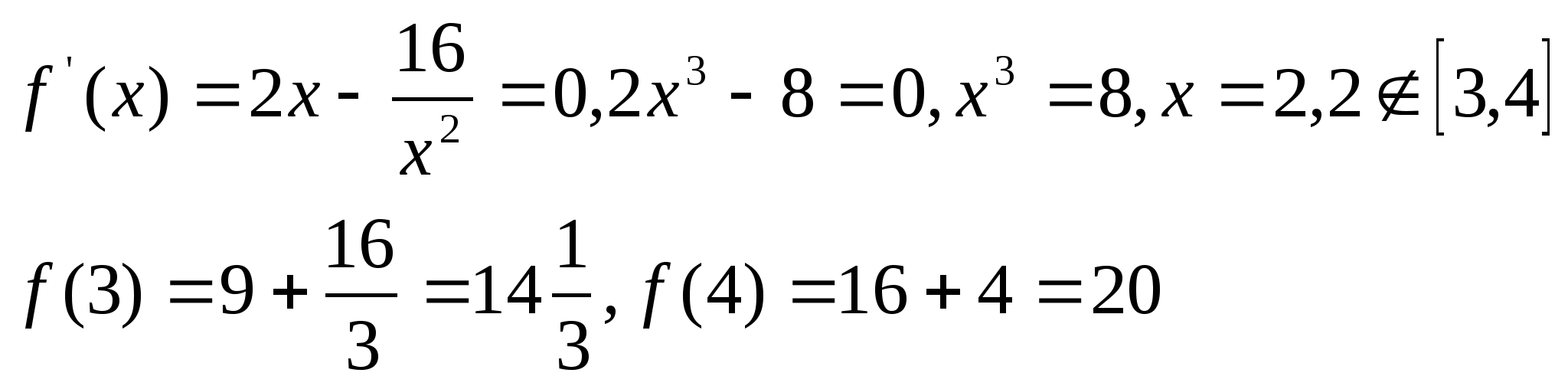
Ответ:![]()
Пример 3. Исследовать на монотонность,
найти локальные экстремумы и построить эскиз графика функции
![]()
Решение.
![]()
![]() точки
экстремума,
точки
экстремума,
![]()
![]() -экстремумы
функции,
-экстремумы
функции,
![]() -
промежутки возрастания,
-
промежутки возрастания,
![]() -
промежутки убывания.
-
промежутки убывания.
![]()
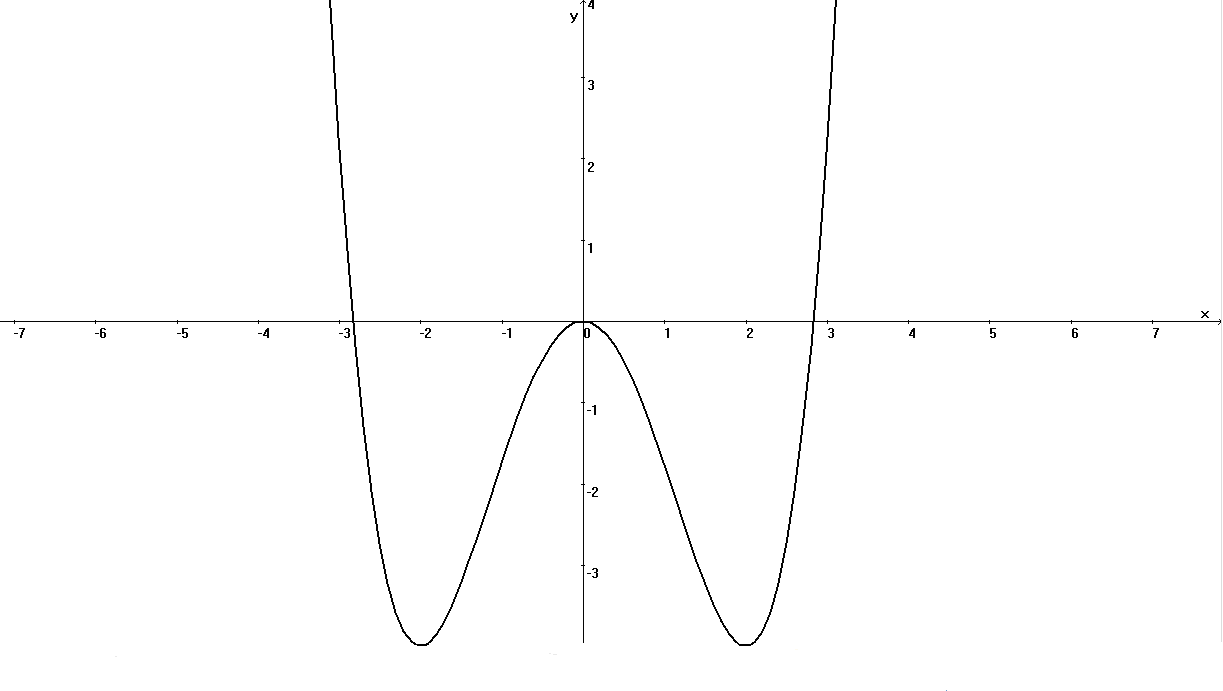
Пример 4. Найти промежутки выпуклости и точки перегиба функции
![]()
Решение.
![]() -
точка перегиба.
-
точка перегиба.
![]() -
выпуклость направленная вверх.
-
выпуклость направленная вверх.
![]() -
выпуклость направленная вниз.
-
выпуклость направленная вниз.
Пример 5. Провести полное исследование свойств и построить эскиз графика функции
![]()
Решение.
![]() -
вертикальная асимптота.
-
вертикальная асимптота.
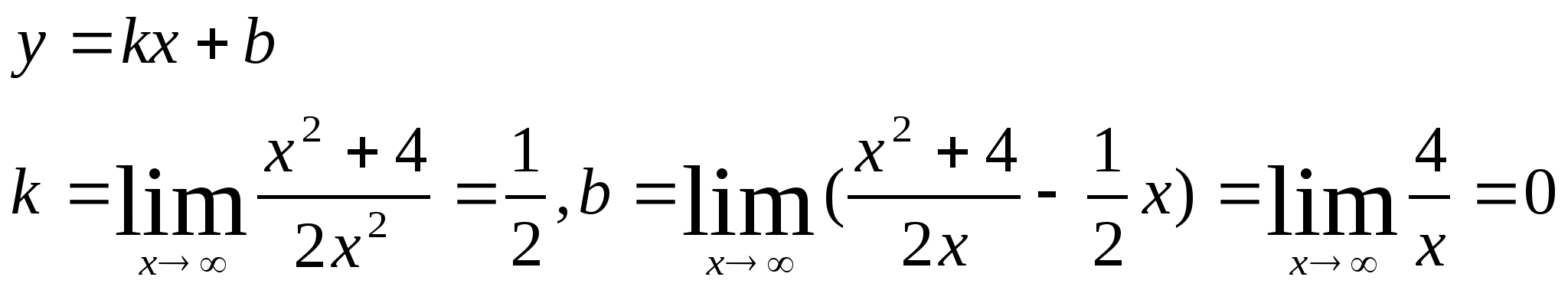
![]() -
горизонтальная асимптота
-
горизонтальная асимптота
![]() -
функция нечетная
-
функция нечетная
Точки пересечения с осями:
с ох, у=0 - нет точек, с оу, х=0 - нет точек.
Точки экстремума:
![]() -
точки экстремума,
-
точки экстремума,
![]() -экстремумы
функции.
-экстремумы
функции.
Точки перегиба:
![]() -
точка перегиба.
-
точка перегиба.
![]()
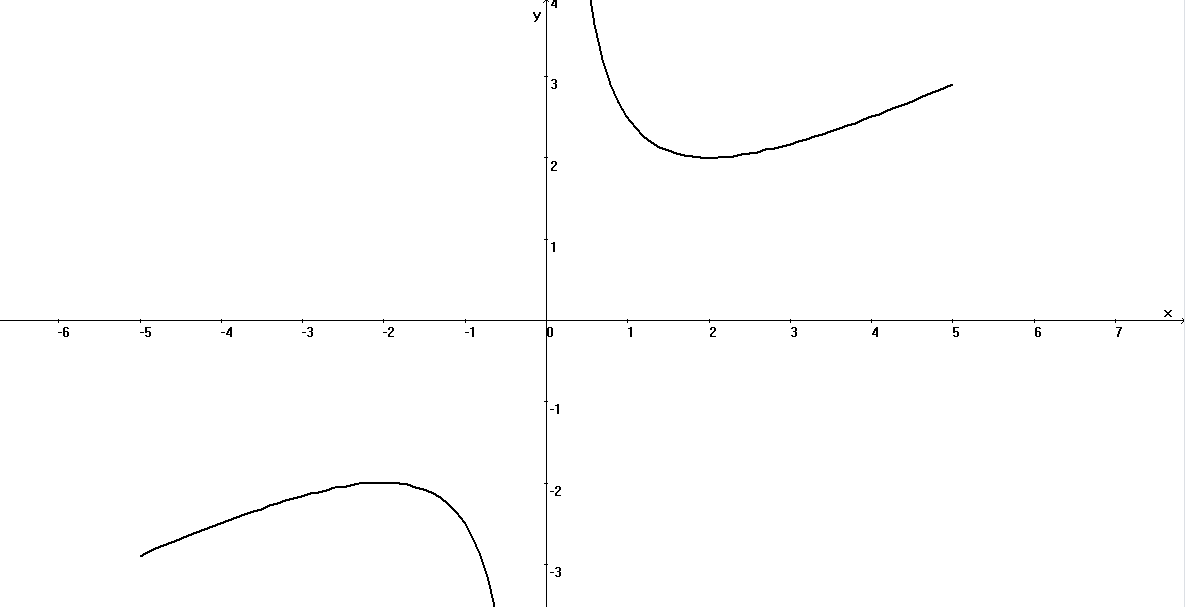
(Смотри видеоуроки 29, 30).
Интеграл
Определение. Функция ![]() называется первообразной функции
называется первообразной функции ![]()
, если ее производная равна ![]()
![]() .
.
Определение. Если ![]() -
некая первообразная для функции
-
некая первообразная для функции ![]() , то
, то
![]() ,
где С - некая постоянная, дает нам совокупность всех первообразных
функции
,
где С - некая постоянная, дает нам совокупность всех первообразных
функции ![]() и
называется неопределенным интегралом функции
и
называется неопределенным интегралом функции ![]()
Обозначение его ![]()
Основные свойства неопределенного интеграла:
1.![]()
2.![]()
3.![]()
4. ![]()
5.![]()
Таблица основных интегралов:
1.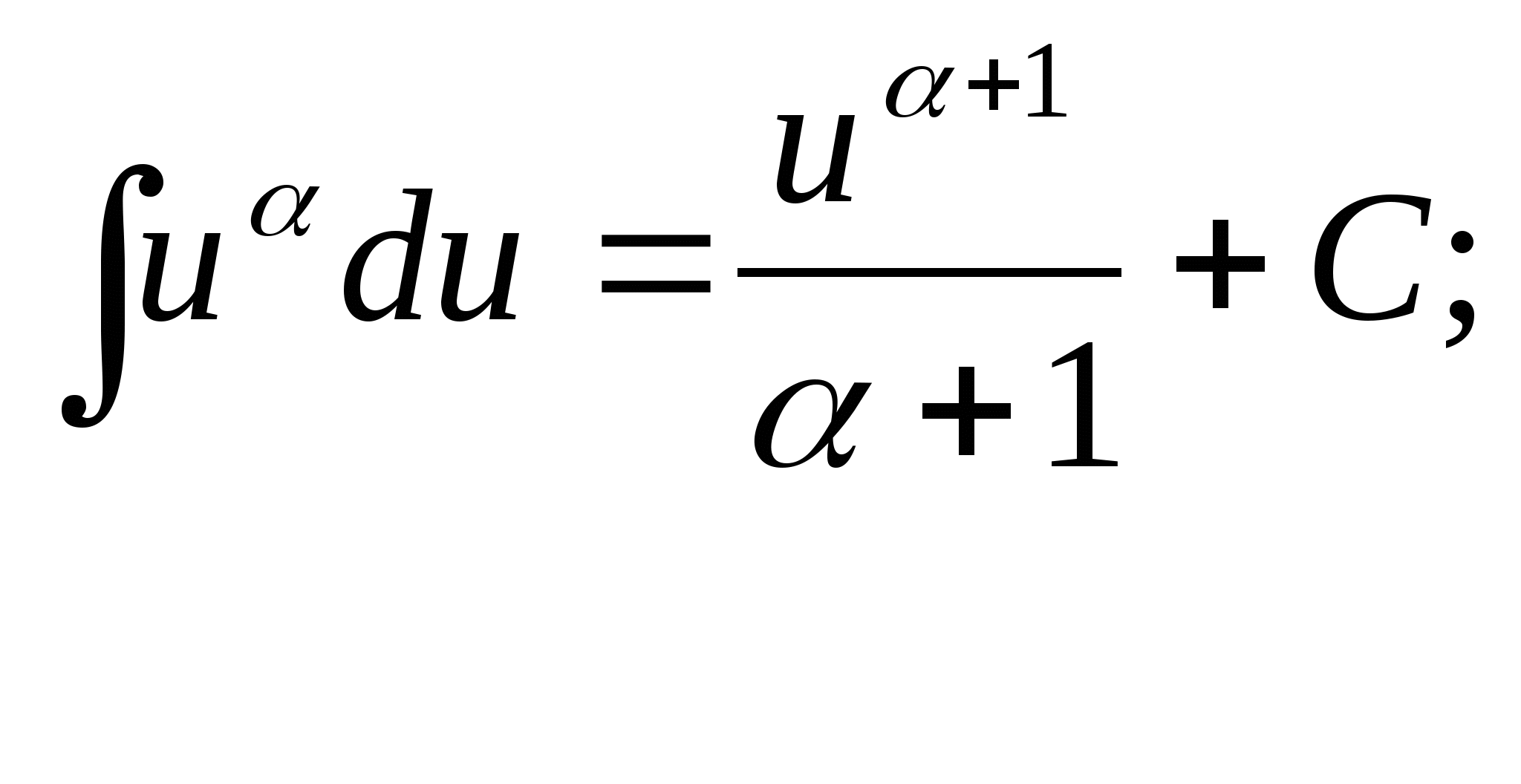 7.
7.![]()
2.![]() 8.
8.![]()
3.![]() 9.
9.![]()
4.![]() 10.
10.![]()
5.![]() 11.
11.![]()
6.![]() 12.
12.
![]()
Формула интегрирования по частям
![]()
Определение. Пусть на замкнутом
промежутке ![]() задана непрерывная функция
задана непрерывная функция ![]() и
и
![]() -
произвольное разбиение отрезка
-
произвольное разбиение отрезка ![]() .
.
Сумма вида ![]() где
где
![]() -
некоторое число из отрезка
-
некоторое число из отрезка ![]() , а
, а
![]() -
длина этого отрезка, называется интегральной суммой функции
-
длина этого отрезка, называется интегральной суммой функции
![]() на
отрезке
на
отрезке ![]() .
.
Определенным интегралом от функции
![]() на
отрезке
на
отрезке ![]() называется предел последовательности интегральных сумм при
бесконечном дроблении отрезка
называется предел последовательности интегральных сумм при
бесконечном дроблении отрезка ![]() ,
обозначают
,
обозначают 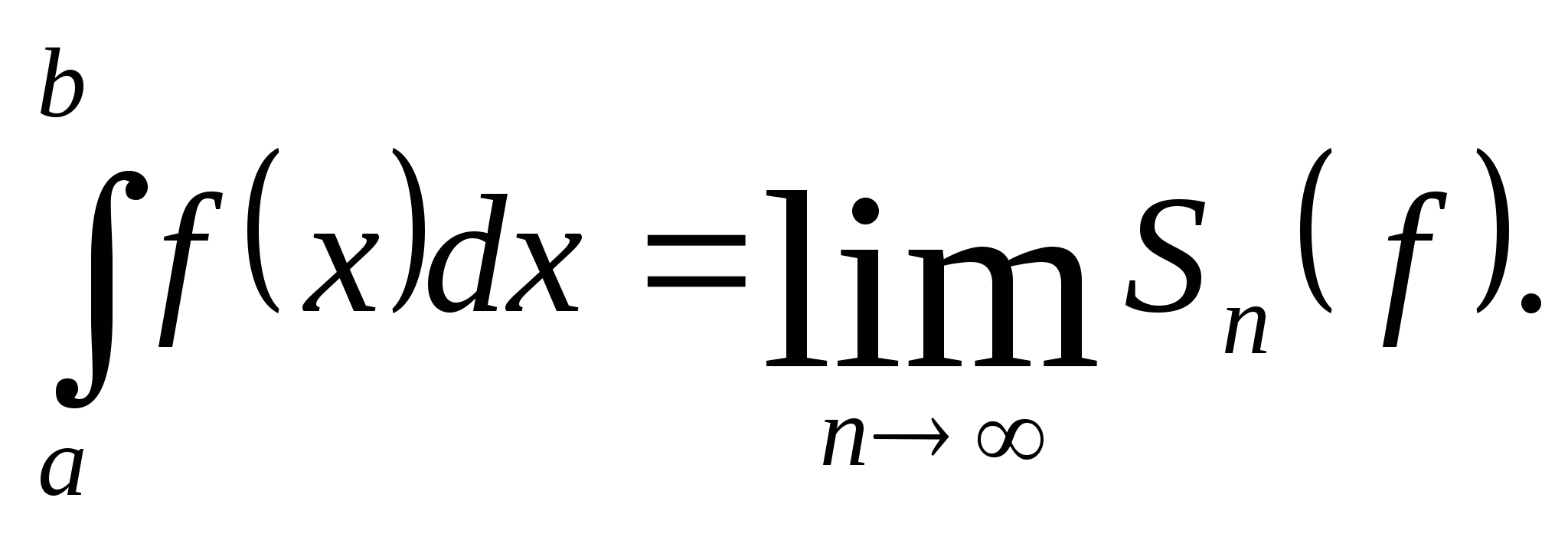
Формула Ньютона-Лейбница: 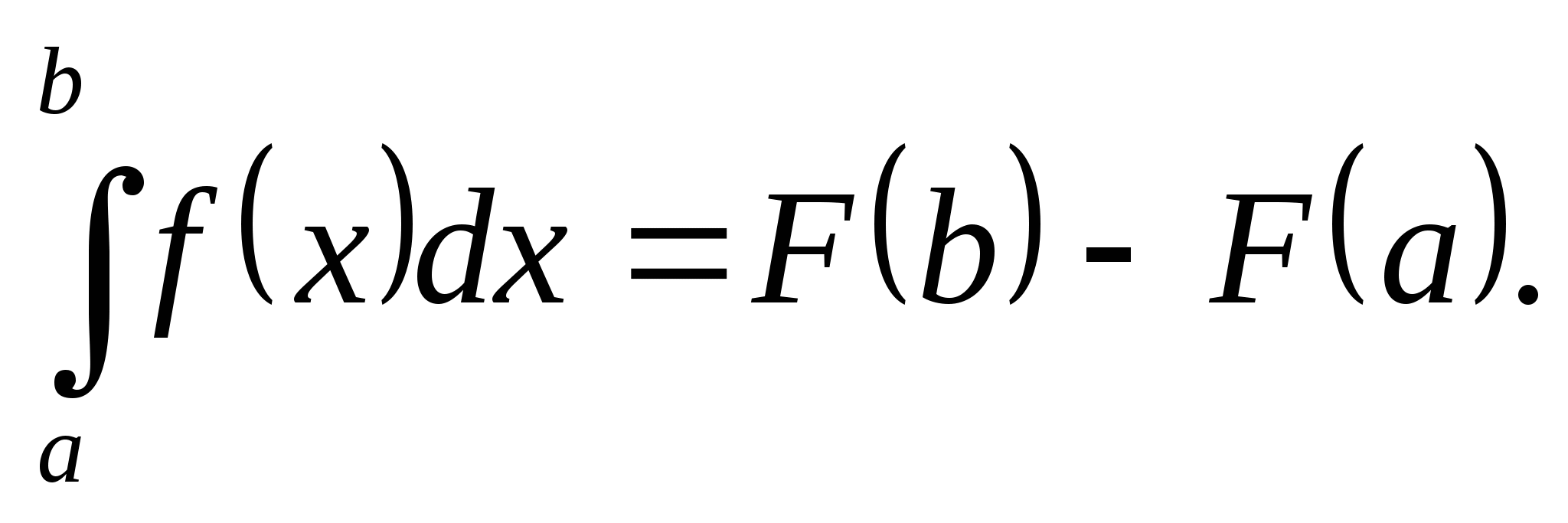
Пример 1. Вычислить интеграл 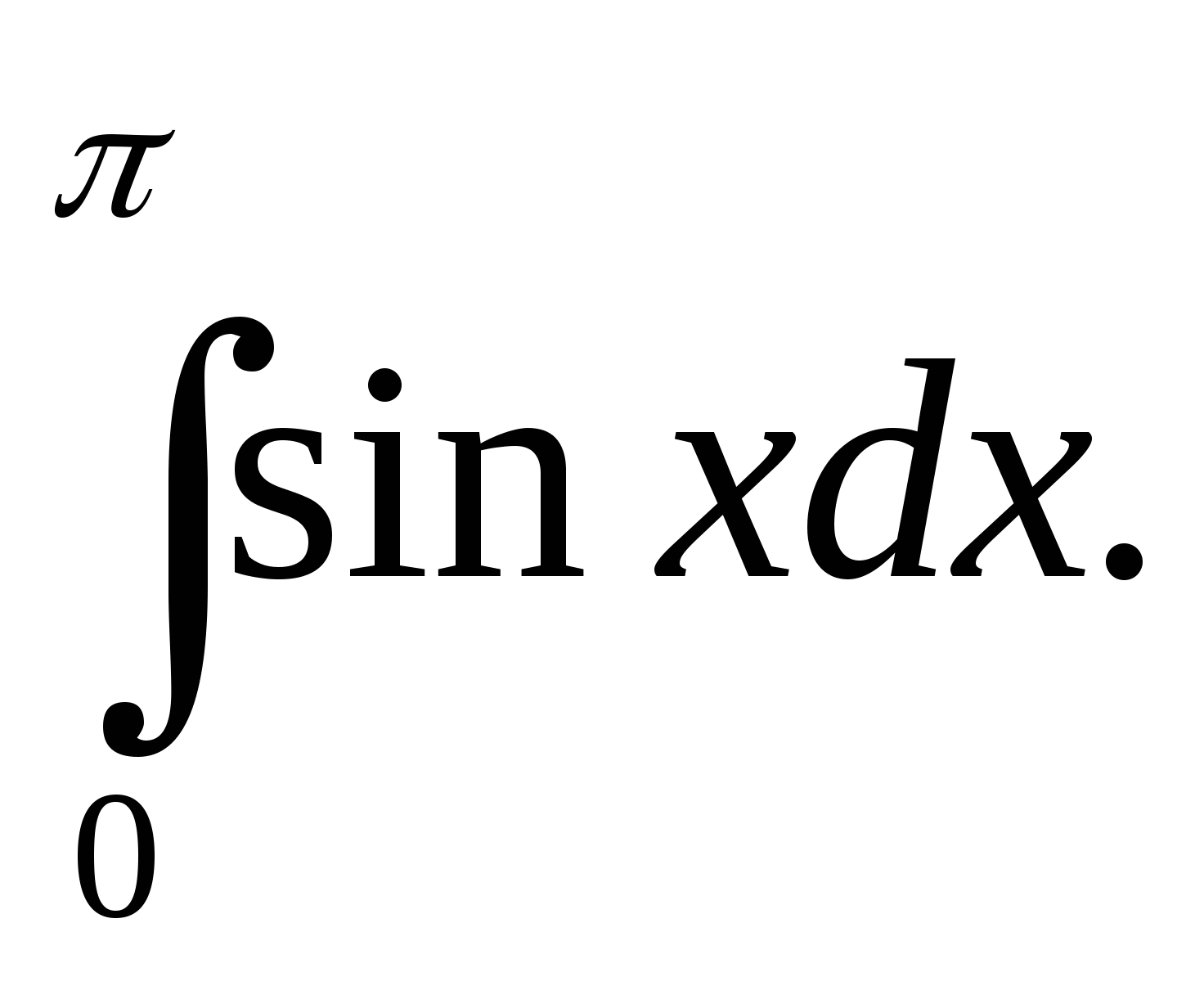
Решение. 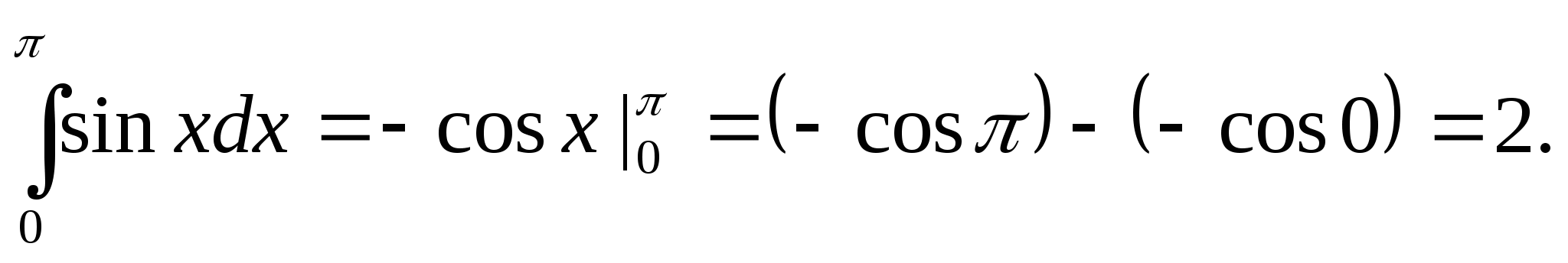
Пример 2. Найти неопределенный интеграл
1)![]()
Решение.
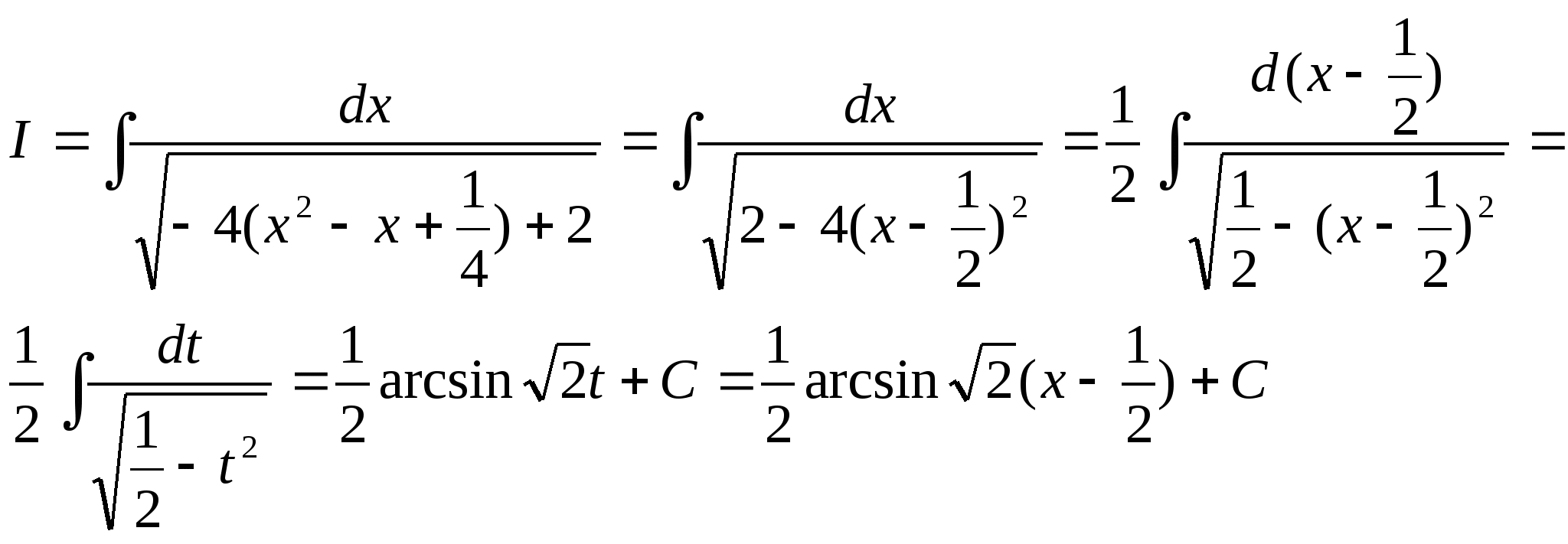
![]() Ответ:
Ответ:![]()
2)![]()
Решение.
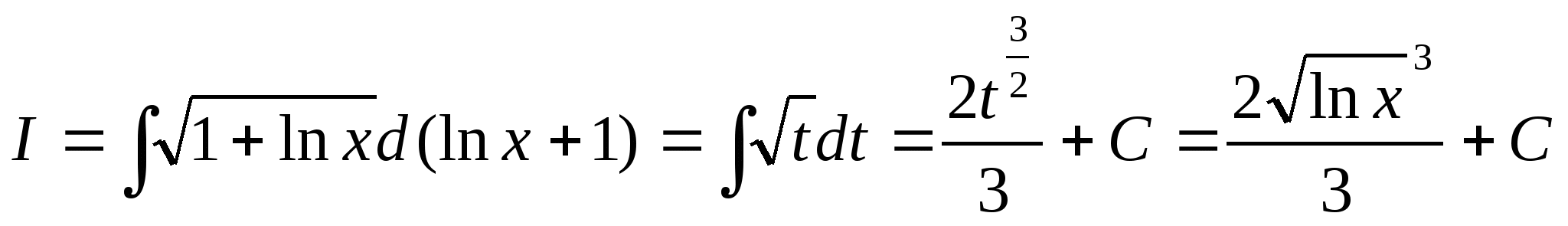
Ответ:![]()
3)![]()
Решение.
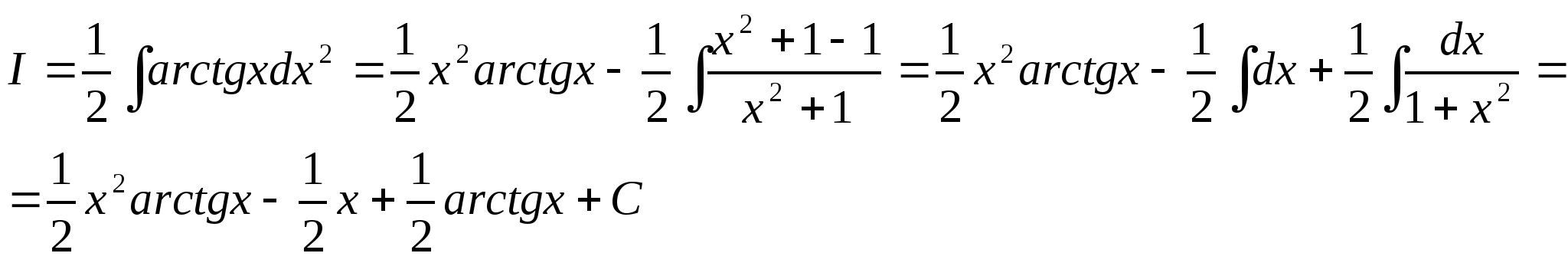
Ответ:![]()
Пример 3. Вычислить 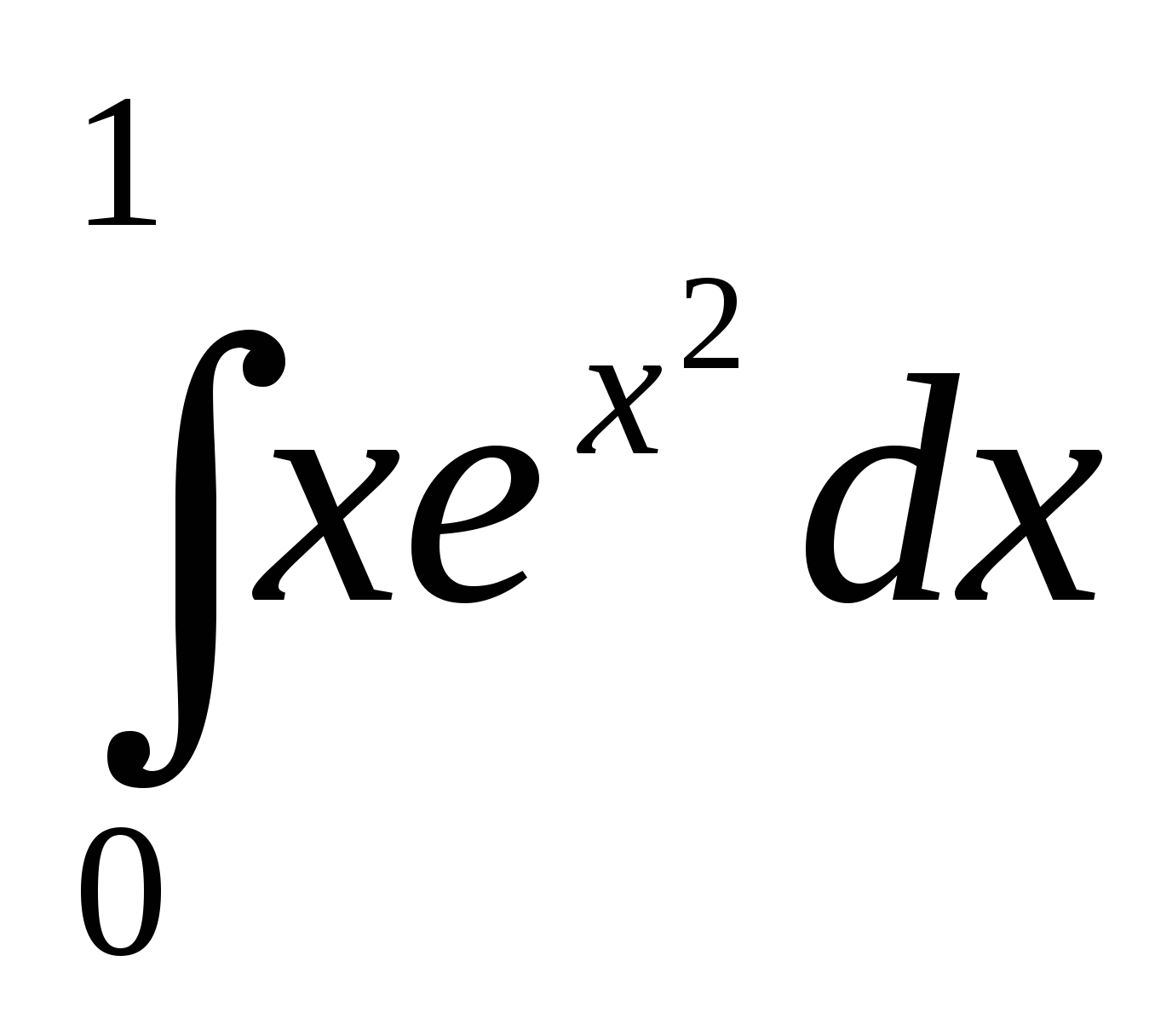
Решение.
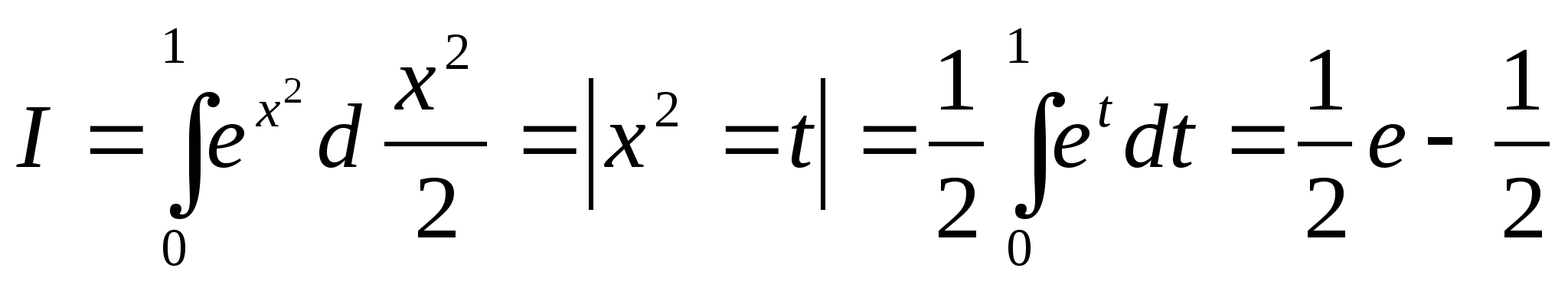
![]()
Ответ:![]()
Пример 4. Определить объем тела вращения
вокруг оси абсцисс плоской фигуры, ограниченной кривыми ![]()
Решение.
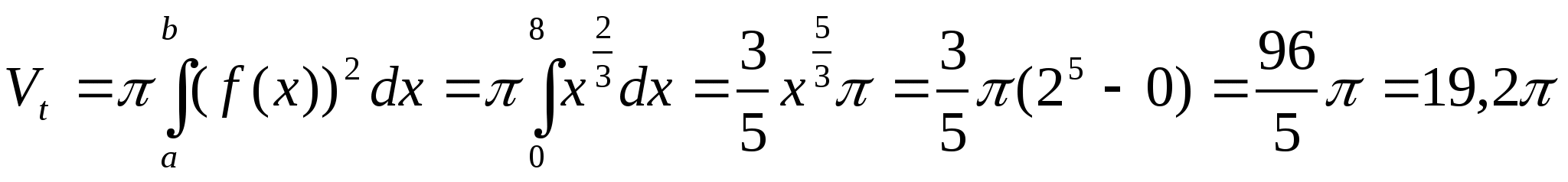
Ответ:![]()
(Смотри видеуроки 13, 14).
4. КОМБИНАТОРИКА
Основные понятия и формулы
Какое-либо упорядоченное множество, которое
состоит из ![]() элементов, называется перестановкой из
элементов, называется перестановкой из ![]() элементов, и обозначается
элементов, и обозначается ![]()
Формула перестановки ![]()
Размещением из ![]() элементов по
элементов по ![]() ,
называется некоторое упорядоченное подмножество из
,
называется некоторое упорядоченное подмножество из ![]() элементов множества из
элементов множества из ![]() элементов.
элементов.
Формула размещений ![]()
Сочетанием из ![]() по
по
![]() называется некое подмножество из
называется некое подмножество из ![]() элементов некоторого множества из
элементов некоторого множества из ![]() .
.
Формула сочетаний ![]()
Свойства сочетаний:
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Перестановки с повторением, если среди n
элементов есть одинаковые, и если среди них ![]() -
первого типа,
-
первого типа, ![]() - другого типа и т. д., то получаем формулу для перестановок с
повторением.
- другого типа и т. д., то получаем формулу для перестановок с
повторением.
Формула перестановки с повторением ![]()
Размещение с повторением - это упорядоченное подмножество, дге элементы не обязательно должны быть разными.
Формула размещение с повторением: ![]() .
.
Сочетания с повторением - это подмножество, элементы которого не обязательно должны быть разными.
Формула сочетания с повторением: ![]()
Пример 1. Сколько трехзначных чисел можно записать цифрами 0,1,2,3,4?
Решение.
Первая цифра в трехзначном числе может быть
выбрана 4 способами (0 не выбирается), другая цифра 5 способами,
третья тоже 5 способами. По правилу произведения все три цифры
можно выбрать ![]()
Пример 2. Сколькими способами 7 человек могут встать в очередь в кассу?
Решение.
Число ![]() равно числу перестановок из 7 элементов.
равно числу перестановок из 7 элементов. ![]()
Пример 3. Сколькими способами можно из 7 человек выбрать комиссию из 3 человек?
Решение.
Поскольку порядок среди выбранных в комиссию
человек не важен, то число способов равно сочетанию из 7 по 3.
![]()
Пример 4. Сколько разных слов можно образовать перестановками букв в слове «математика»?
Решение.
В слове «математика» - 10 букв, из них буква «м» повторяется 2 раза, «а» - 3 раза, «т» - 2 раза. Тогда используя формулу перестановок с повторением получим ответ:
![]()
Пример 5. Автомобильный номер состоит из двух букв и 4 цифр. Какое число номеров можно составить, если буквы выбирают из 33 букв украинского алфавита?
Решение.
Найдем отдельно комбинации для букв и отдельно для чисел.
Для букв используем размещения с повторением:
![]()
Для цифр: ![]() Тогда
Тогда ![]()
Пример 6. Сколькими способами можно выбрать 6 одинаковых или разных пирожных в кондитерской, где есть 11 разных сортов пирожных?
Решение.
Используем сочетания с повторениями:
![]()
1.2.Бином Ньютона
Бином (двучлен) - выражение вида
![]() .
.
Формула бинома Ньютона:
![]() .
.
Правая часть этой формулы называется разложением бинома.
Свойства разложения бинома:
1.Количество членов разложения бинома на единицу больше показателя степени;
2.Все члены разложения имеют одну и ту же степень равную n;
3.Сумма биноминальных коэффициентов равна
![]() ;
;
4.Формула ![]() члена
разложения имеет вид:
члена
разложения имеет вид: ![]() .
.
Пример 1. В разложении ![]() четвертый член равен 0,96. Найти значение
четвертый член равен 0,96. Найти значение ![]() если сумма биноминальных коэффициентов равна 1024.
если сумма биноминальных коэффициентов равна 1024.
Решение.
Так как сумма биноминальных коэффициентов равна
![]() то
то
![]() Теперь используем формулу члена разложения:
Теперь используем формулу члена разложения:
![]() По
условию
По
условию ![]()
Пример 2. При каких значениях ![]() возможно равенство:
возможно равенство:
![]() ?
?
Решение.
![]() Из
второг уравнения имеем
Из
второг уравнения имеем ![]() ,
тогда
,
тогда ![]() Из
второго находим
Из
второго находим ![]() .
.
Так как ![]() .
Второй корень не подходит, тогда
.
Второй корень не подходит, тогда ![]()
(Смотри видеуроки 22, 24, 25).
5. СТАТИСТИКА
Основные характеристики выборки
Статистика - это наука, изучающая, обрабатывающая и анализирующая количественные данные о разнообразнейших массовых явлений в жизни.
Экономическая статистика изучает изменение цен, спроса и предложения товаров, прогнозирует рост и падение производства и потребления.
Математическая статистика - это раздел математики, изучающий математические методы обработки и использования статистических данных для научных и практических выводов.
Генеральная совокупность - это вся совокупность однородных объектов, которую изучают относительно некоторого признака, который характеризует эти объекты.
Выборкой называют совокупность случайно выбранных объектов из генеральной выборки.
Статистическим распределением называют перечисление вариант и соответствующих им частот.
Эмпирической функцией распределения
называют функцию ![]() ,
которая определяет для каждого х относительную частоту
,
которая определяет для каждого х относительную частоту ![]() , то
есть
, то
есть ![]() где
где
![]() -
число вариант меньших х,
-
число вариант меньших х, ![]() -
объем выборки.
-
объем выборки.
Основные числовые характеристики выборки:
Медиана - это так называемое среднее
значение упорядоченного ряда значений случайной величины: ![]()
Мода - это вариант, который имеет большую частоту, встречается чаще других.
Размах выборки - это разность между наибольшим и наименьшим значениями случайной величины выборки.
Среднее выборочное - 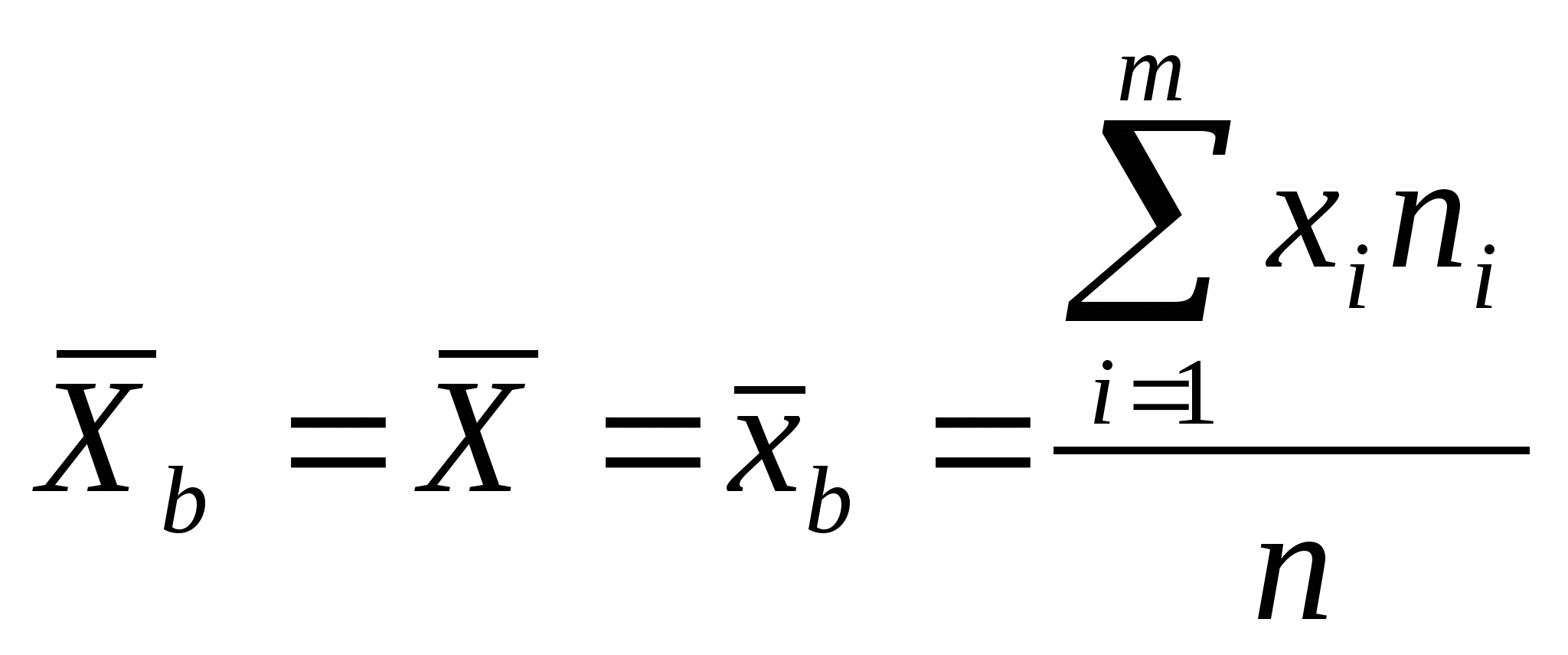
Дисперсия - 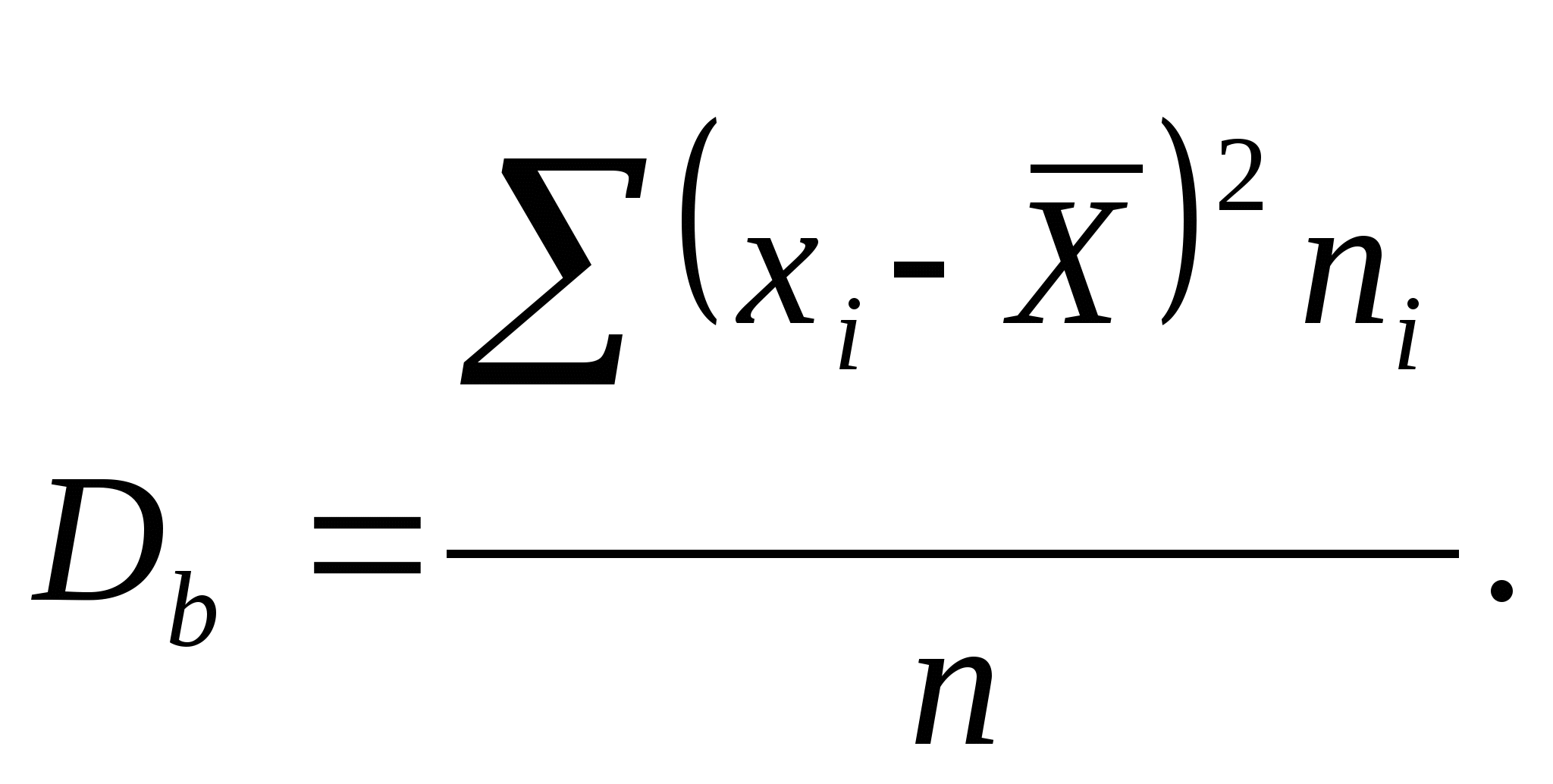
Среднее квадратичное отклонение -
![]()
Коэффициент вариации - ![]()
Подобно тому, как графики всех парабол можно
получить с помощью геометрических преобразований одной параболы
![]() ,
так и все кривые нормальных распределений можно получить с помощью
геометрических преобразований одной кривой. Эту кривую называют
кривой нормального распределения, или гауссовой кривой:
,
так и все кривые нормальных распределений можно получить с помощью
геометрических преобразований одной кривой. Эту кривую называют
кривой нормального распределения, или гауссовой кривой:
![]() .
.
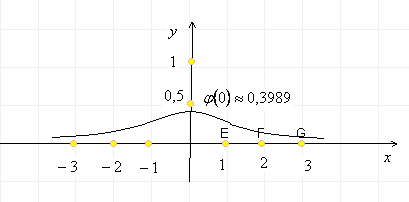
Правило трех сигм:
68% (или приблизительно ![]() )
всех значений нормального распределения случайной величины Х имеют
отклонение от среднего значения, по абсолютной величине не
превышающее среднее квадратичное отклонение
)
всех значений нормального распределения случайной величины Х имеют
отклонение от среднего значения, по абсолютной величине не
превышающее среднее квадратичное отклонение ![]() , а
96% всех значений - не превышающее
, а
96% всех значений - не превышающее ![]() .
Почти все значения (точнее, 99,7 всех значений) имеют отклонение от
среднего, не превышающего по абсолютной величине утроенное среднее
квадратичное отклонение
.
Почти все значения (точнее, 99,7 всех значений) имеют отклонение от
среднего, не превышающего по абсолютной величине утроенное среднее
квадратичное отклонение ![]() .
.
Пример 1. Найдите размах, моду, медиану и
среднее значение ряда данных некоторой случайной величины ![]() 1,
1, 2, 2, 2, 3, 4, 4, 5. Постройте полигон частот значений случайной
величины
1,
1, 2, 2, 2, 3, 4, 4, 5. Постройте полигон частот значений случайной
величины ![]() .
Укажите на рисунке размах, моду, медиану заданного ряда данных.
.
Укажите на рисунке размах, моду, медиану заданного ряда данных.
Решение.
Размах выборки: ![]() .
.
Среднее значение: ![]() .
.
Мода выборки: ![]() ,
так как число 2 повторяется чаще всего.
,
так как число 2 повторяется чаще всего.
Медиана: ![]() ,
так как именно это число стоит в центре ряда.
,
так как именно это число стоит в центре ряда.
Постоим полигон частот.
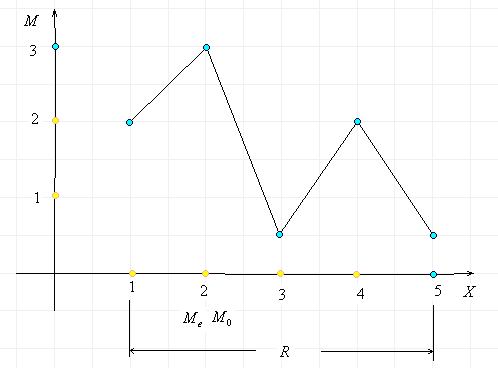
Пример 2. Выигрыши (в грн.), которые приходятся на один билет в каждой их двух лотерей, имеют следующие законы распределения:
1)Х
0
1
5
10
Р
0,9
0,06
0,03
0,01
2)Х
0
1
5
10
Р
0,85
0,12
0,02
0,01
Какой из этих лотерей вы отдадите предпочтение?
Решение.
Найдем математическое ожидание каждого распределения.
1)![]() .
.
2)![]() .
.
Сравним два числа и получим, что вторая выгодней.
Пример 3. Задана генеральная совокупность из 20 элементов. Выполнить задания:
1) построить статистическое распределение и ее эмпирическую функцию распределения;
2) вычислить ее числовые характеристики выборки: среднее, дисперсию и среднее квадратичное отклонению
Решение.
Дана генеральная выборка:
15,19,13,12,9,14,15,19,12,17,13,9,15,12,15,14,18,16,15,12.
1) Статистическое распределение выборки имеет вид:
9
12
13
14
15
16
17
18
19
![]()
2
4
2
2
5
1
1
1
2
![]()
![]() Эмпирическая
функция распределения имеет вид:
Эмпирическая
функция распределения имеет вид:
![]() где
где
![]() -
число вариантов, меньших чем х;
-
число вариантов, меньших чем х; ![]() -
объем выборки;
-
объем выборки; ![]() Тогда имеем:
Тогда имеем:
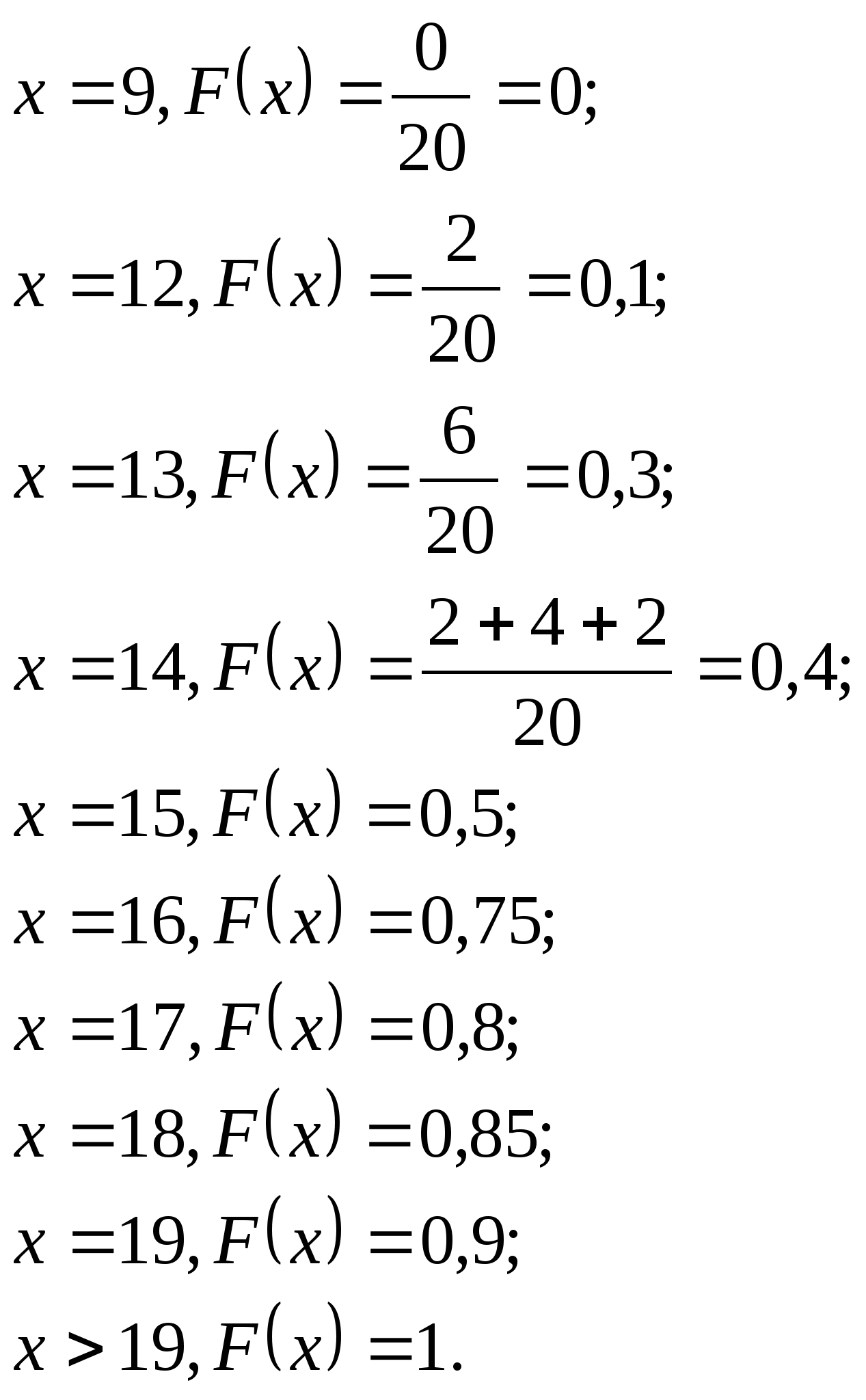 или
или
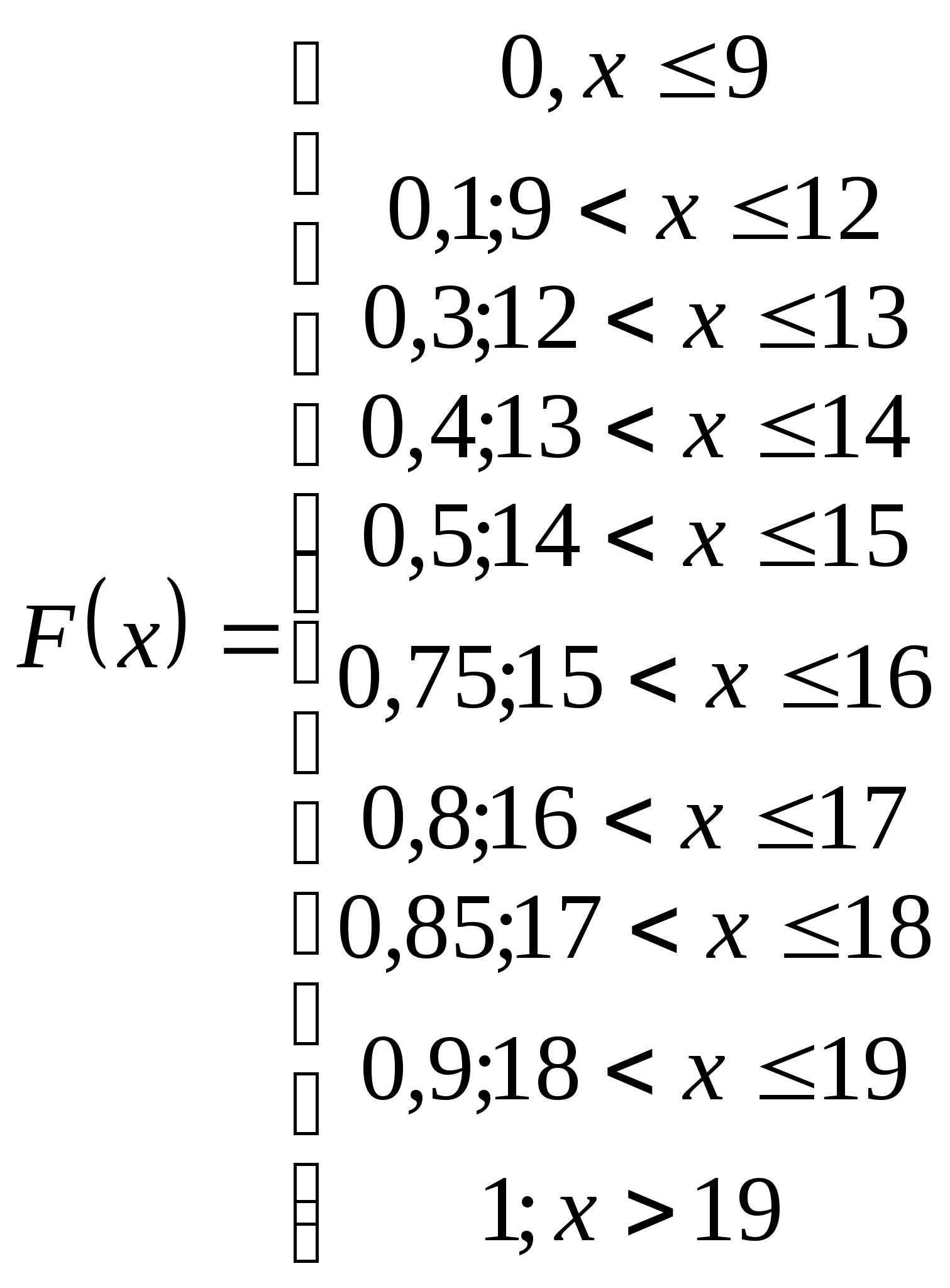
2) Числовые характеристики выборки:
Среднее ![]()
Выборочная дисперсия ![]()
![]()
Среднее квадратичное отклонение ![]()
(Смотри видеурок 19).
6.СПРАВОЧНЫЙ МАТЕРИАЛ
Арифметическая прогрессия
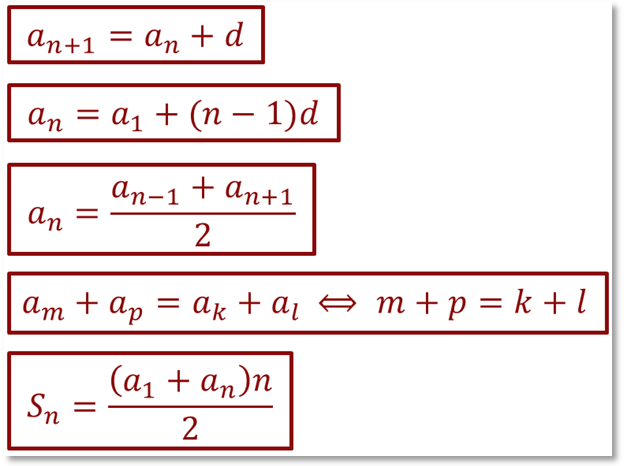
Геометрическая прогрессия

Свойства логарифмов
Если 𝑎, 𝑏, 𝑐 − положительные числа, причем 𝑎≠1, то справедливы равенства:
![]()
![]()
![]() ,
для любого
,
для любого ![]()
![]() ,
для любого
,
для любого ![]()
![]()
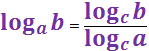 -
формула перехода к новому основанию логарифма
-
формула перехода к новому основанию логарифма
7.ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
(Смотри видеоуроки 6, 8, 11, 26, 27, 28).
ПРЕОБРАЗОВАНИЕ ВЫРАЖЕНИЙ
1.Сократиь дробь а)![]() б)
б)
![]()
2.Упростить выражение а) ![]() б)
б)
![]()
3.Найти значение выражения а) ![]() б)
б)
![]()
5.Вычислить а) ![]() б)
б)
![]()
7.Упростить выражение а) ![]()
б) ![]()
8.Сократить дробь а) ![]() б)
б)
![]()
9.Упростить выражение а) ![]()
б) ![]()
10.Освободиться от иррациональности в знаменателе
а) ![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
11.Упростить выражение а) ![]()
б) ![]()
12.Упростить выражение а) ![]() б)
б)
![]()
13.Разложить на множители а) ![]() б)
б)
![]()
14.Упростить а) ![]() б)
б)
![]()
15.Разложить на множители а) ![]() б)
б)
![]()
16.Сократить дробь а) ![]() б)
б)
![]()
17.Выразить переменную в из формулы а) ![]() б)
б)
![]()
18.Упростить а) 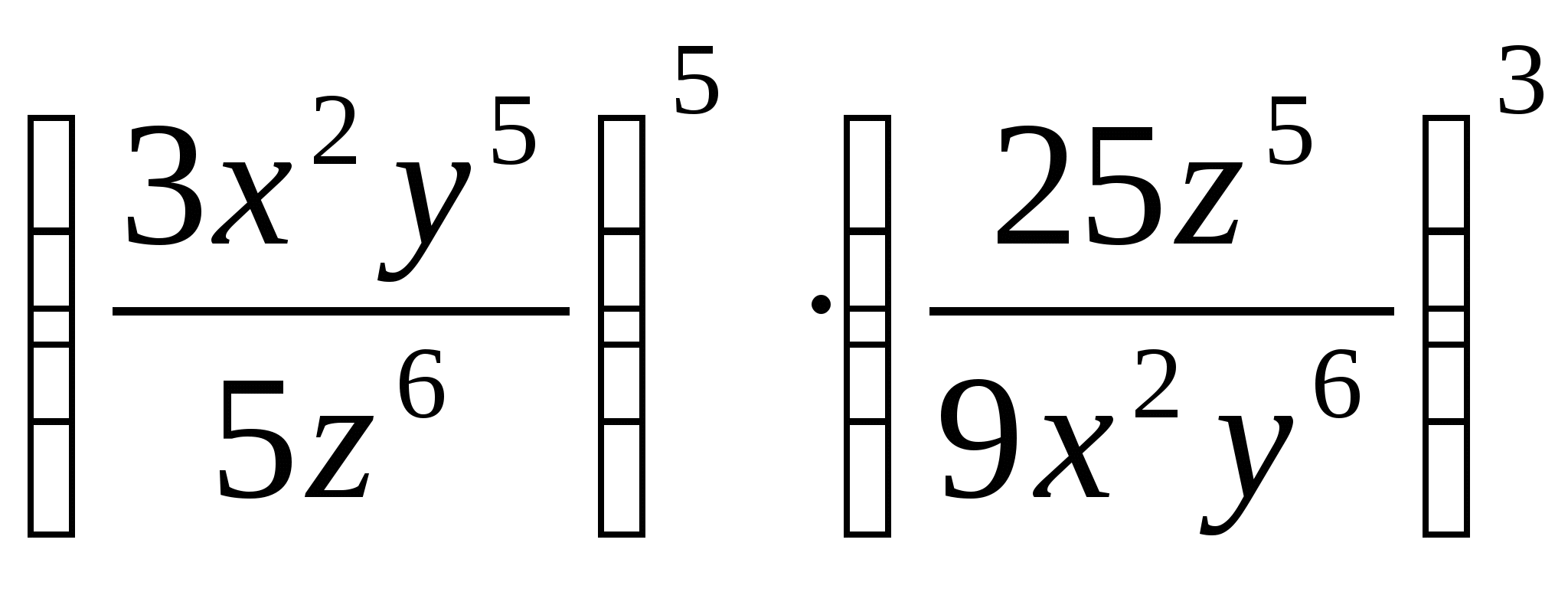 б)
б)
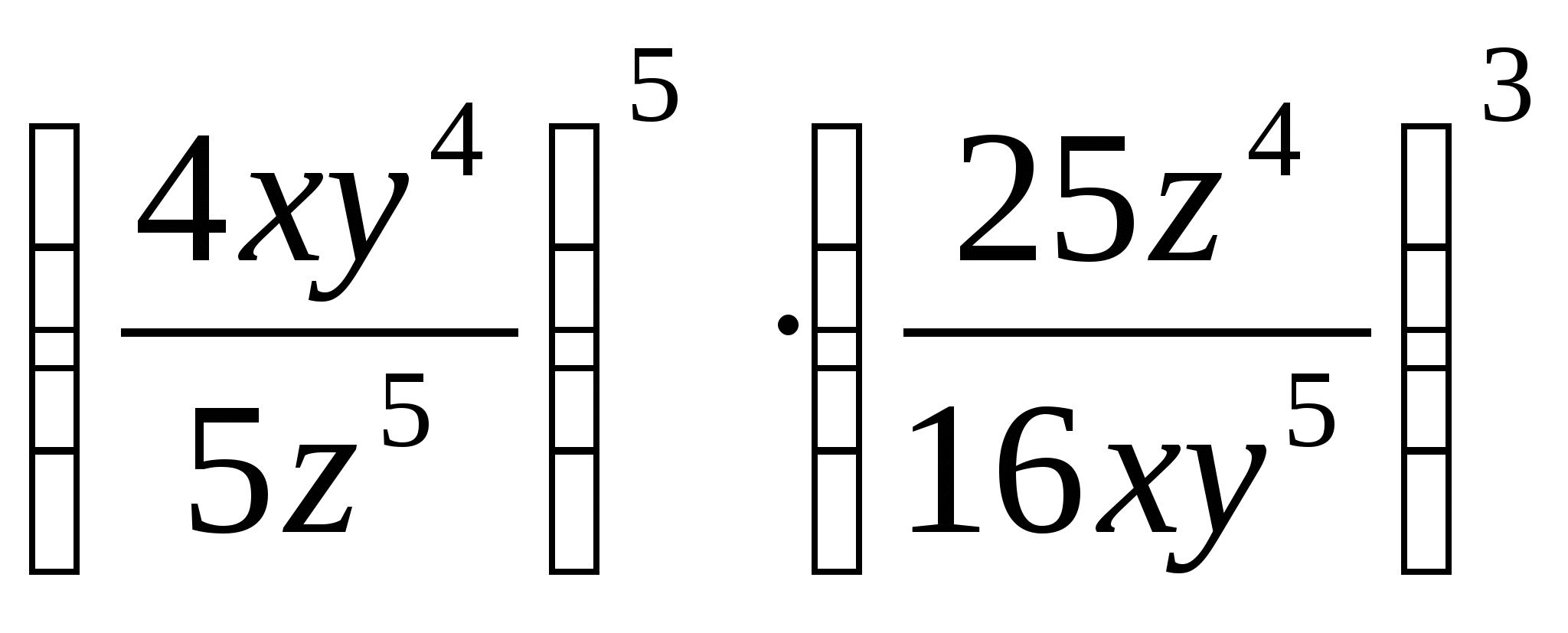
19.Упростить а) 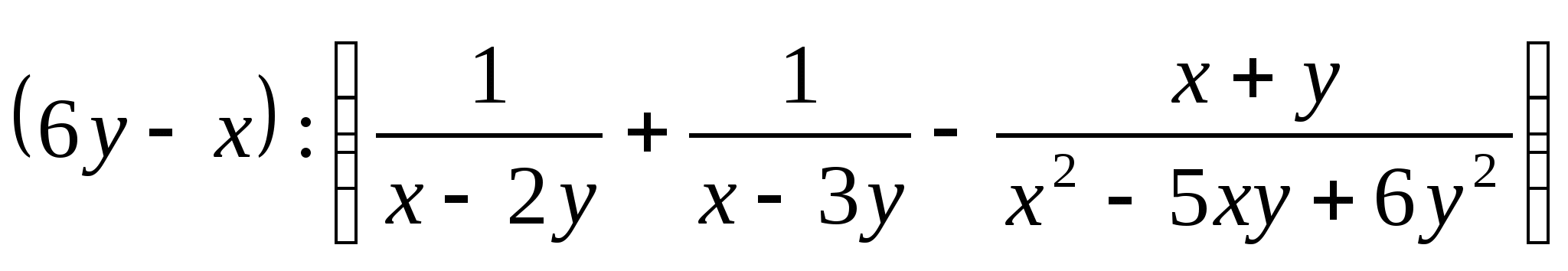
б) 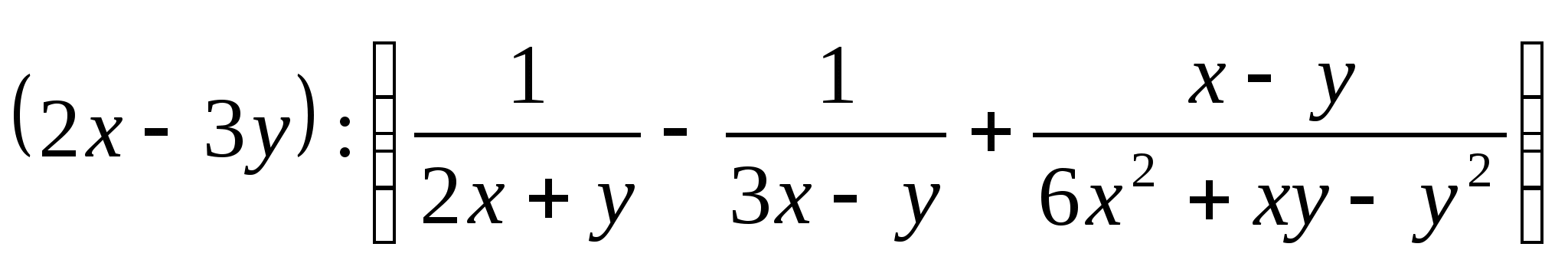
УРАВНЕНИЯ
1.а) ![]() б)
б)
![]()
2.а) ![]() б)
б)
![]()
3.а) ![]() б)
б)
![]()
4.а) ![]() б)
б)
![]()
5.а) ![]() б)
б)
![]()
6.а) ![]() б)
б)
![]()
7. а) ![]() б)
б)
![]()
8. а) ![]() б)
б)
![]()
9. а) ![]() б)
б)
![]()
10. а) ![]() б)
б)
![]()
11. а) ![]() б)
б)
![]()
12. а) ![]() б)
б)
![]()
13. а) ![]() б)
б)
![]()
14.а) ![]() б)
б)
![]()
15. а) ![]()
б) ![]()
16. а) ![]() б)
б)
![]()
17. а) ![]() б)
б)
![]()
СИСТЕМЫ УРАВНЕНИЙ
1.Решите систему уравнений
а) ![]() б)
б)
![]()
2. а) ![]() б)
б)
![]()
3.а) 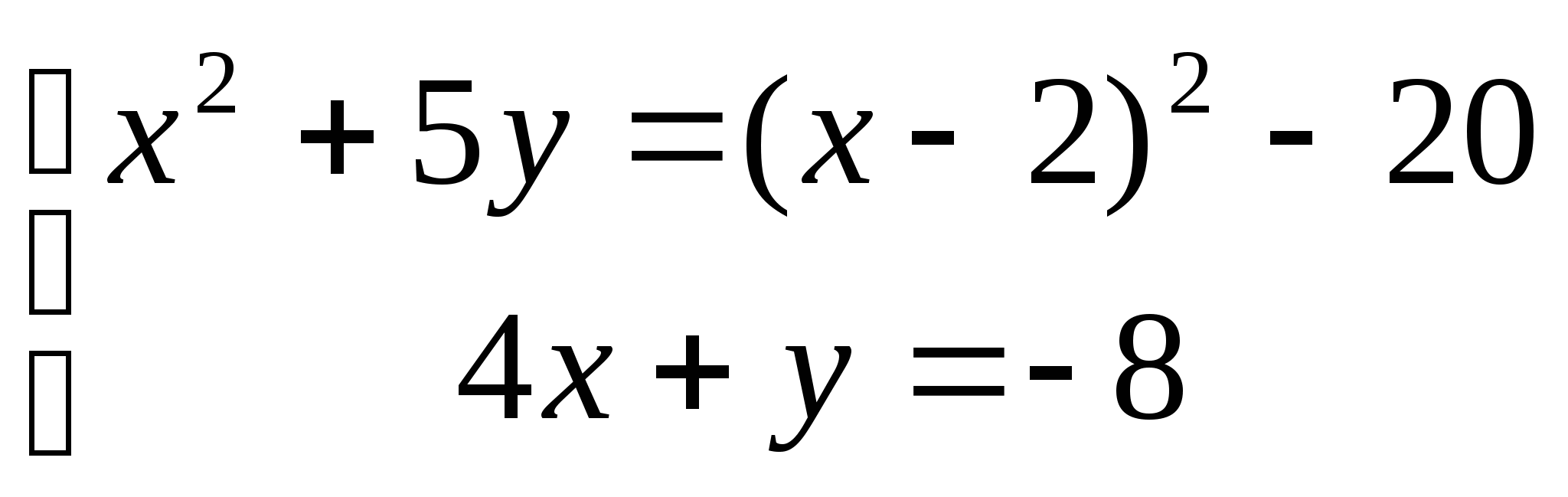 б)
б)
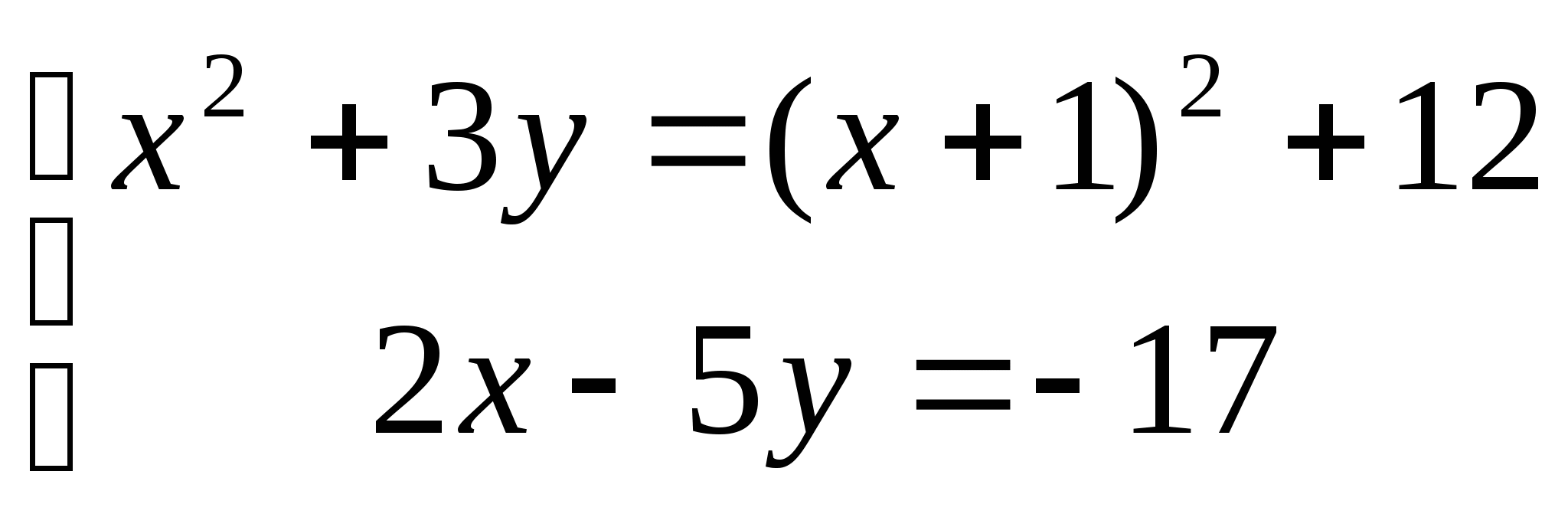
4. а) ![]() б)
б)
![]()
5. а) 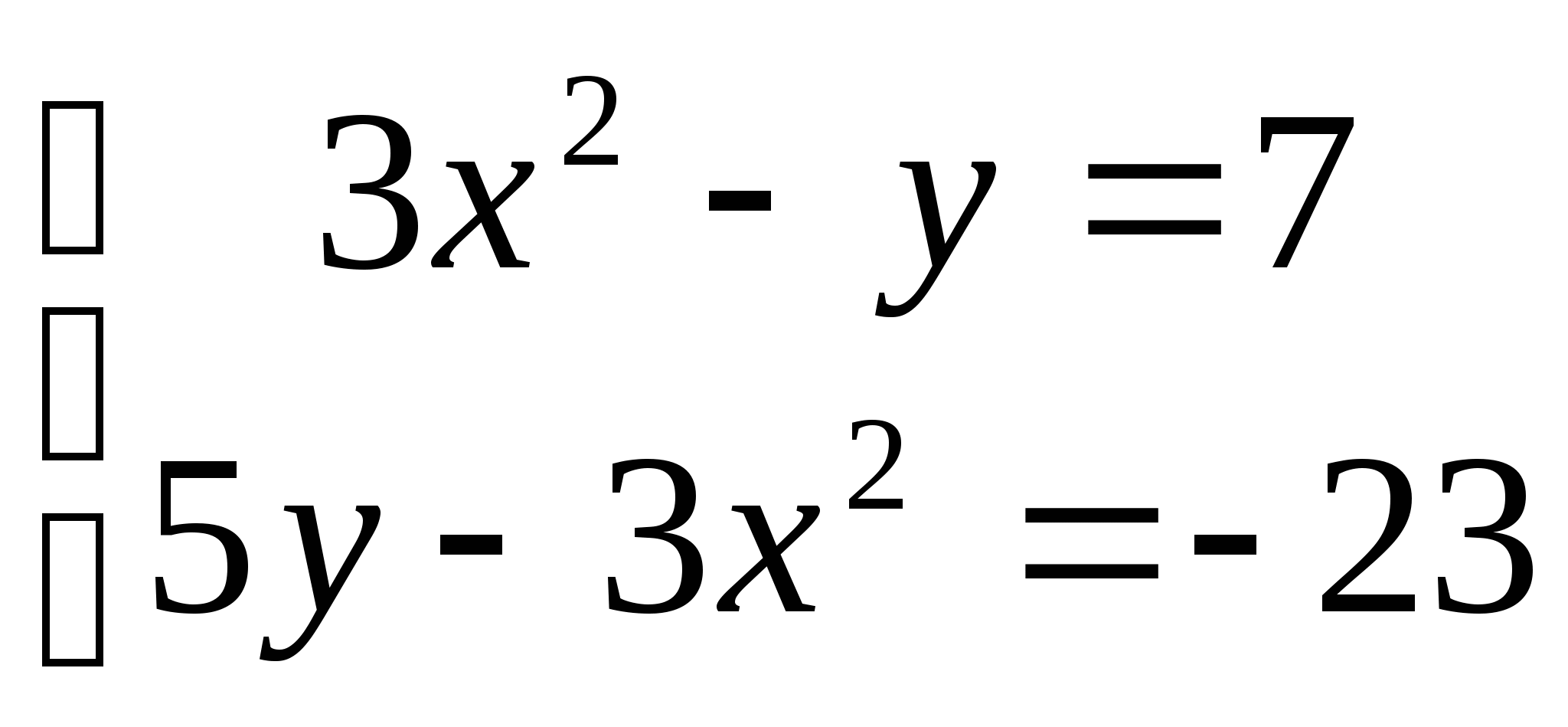 б)
б)
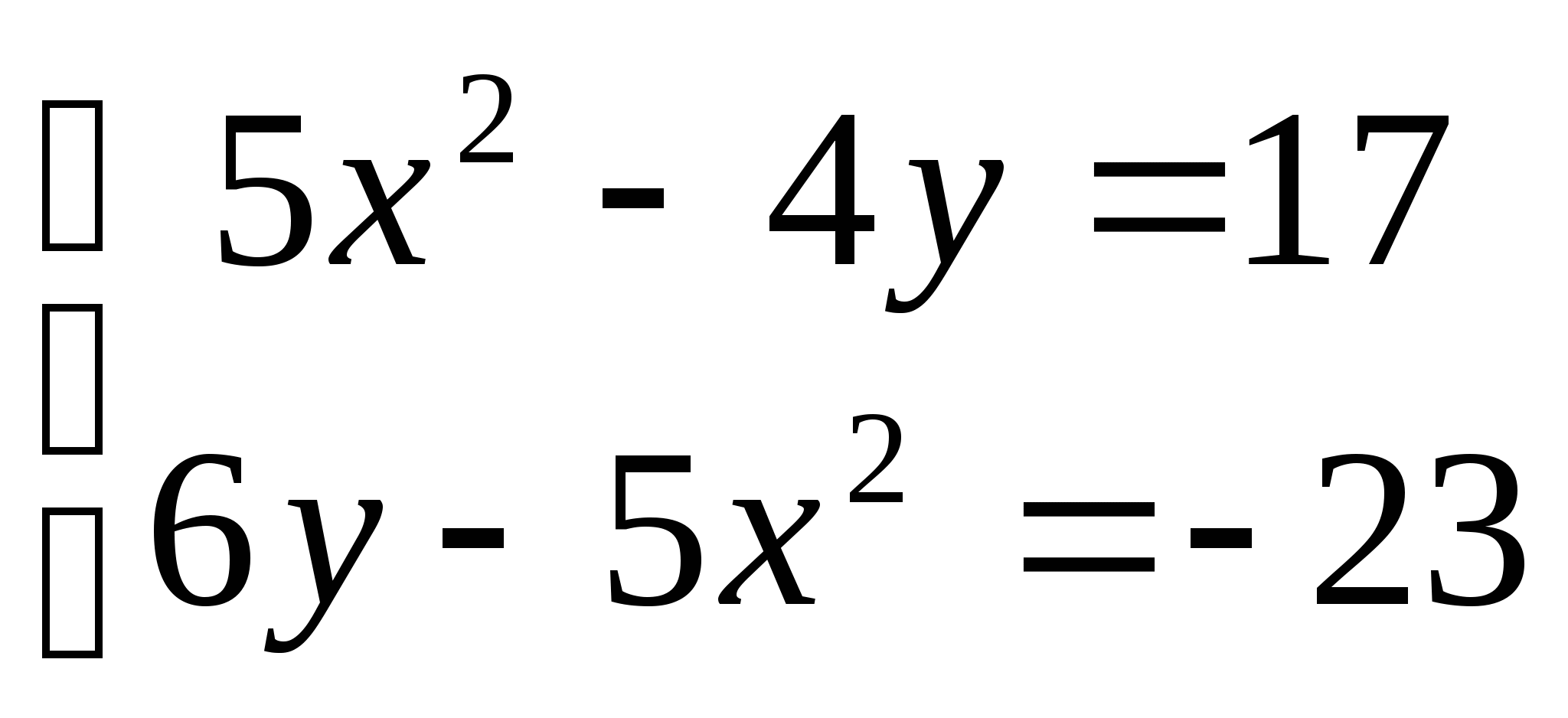
6. а) 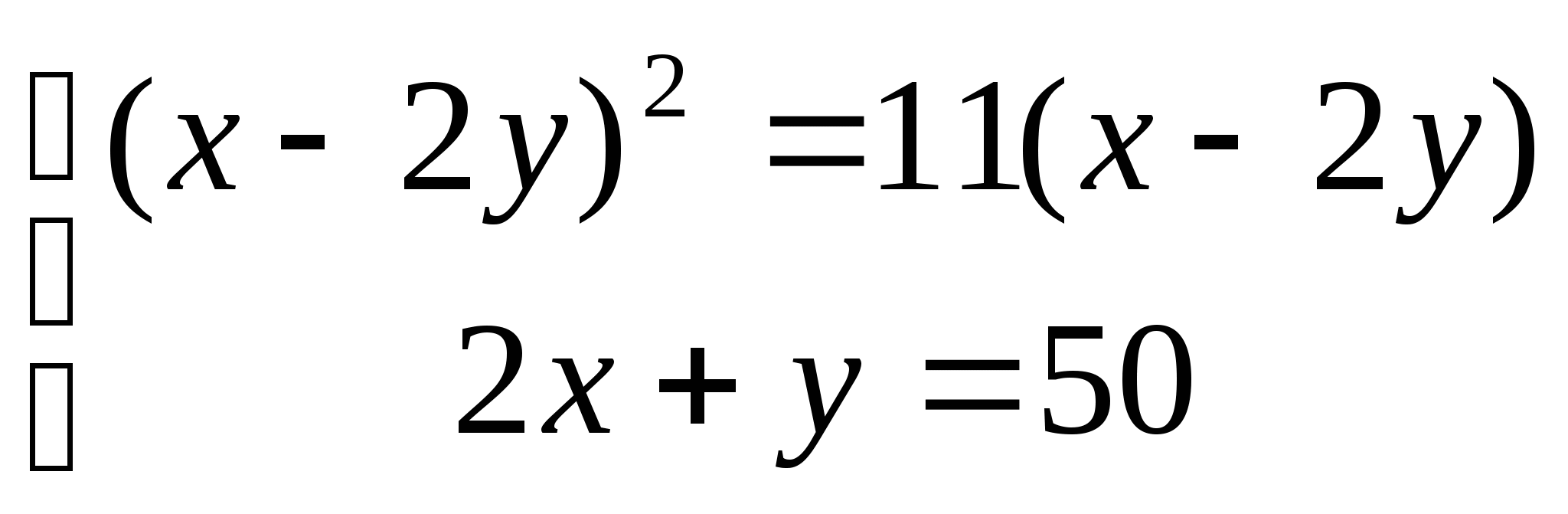 б)
б)
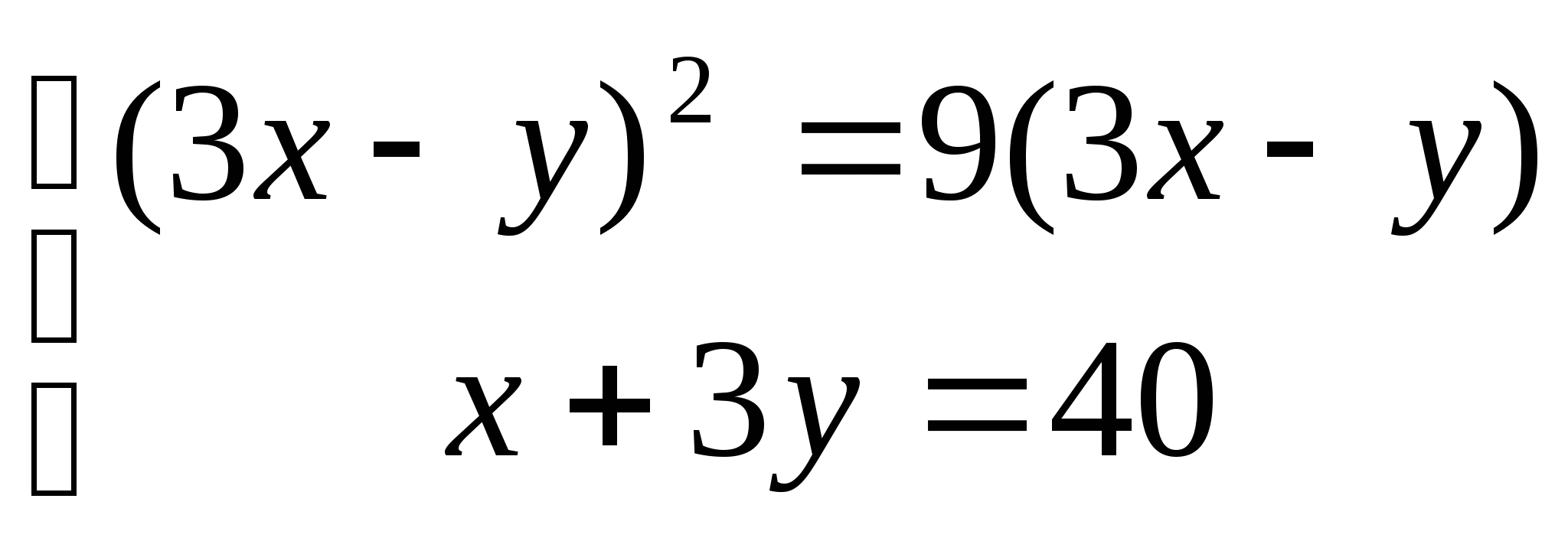
7. а) 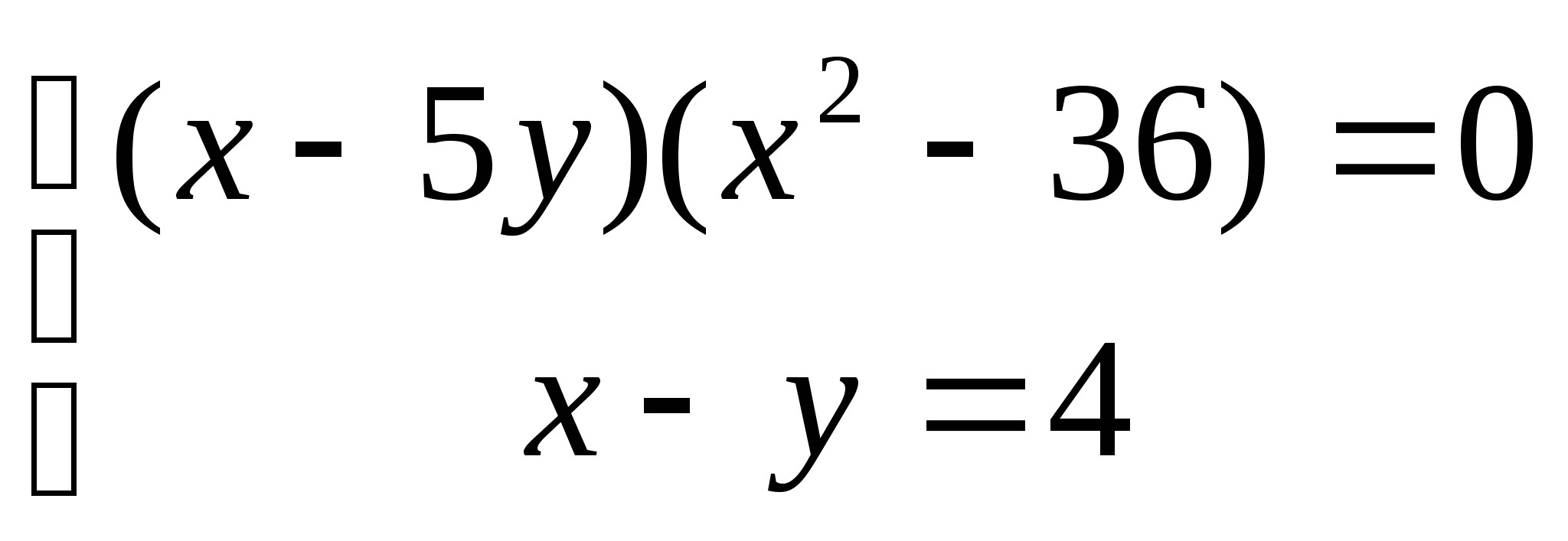 б)
б)
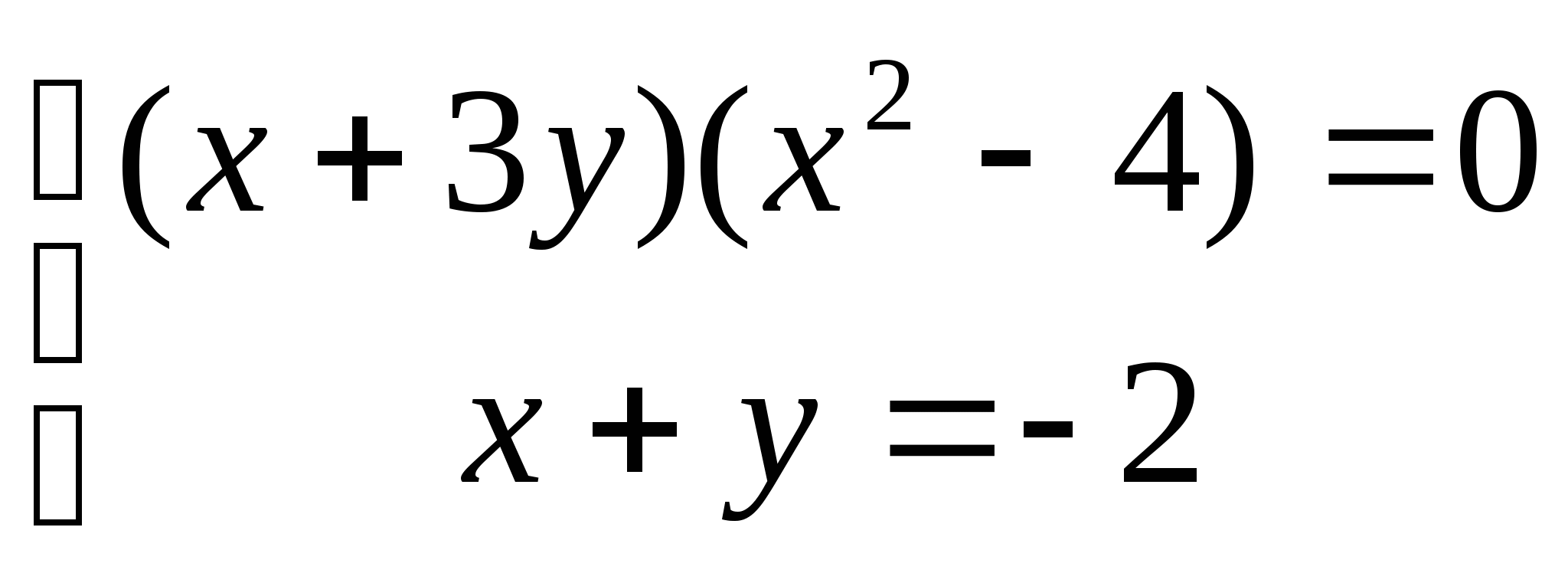
8. а) ![]() б)
б)
![]()
9. а) 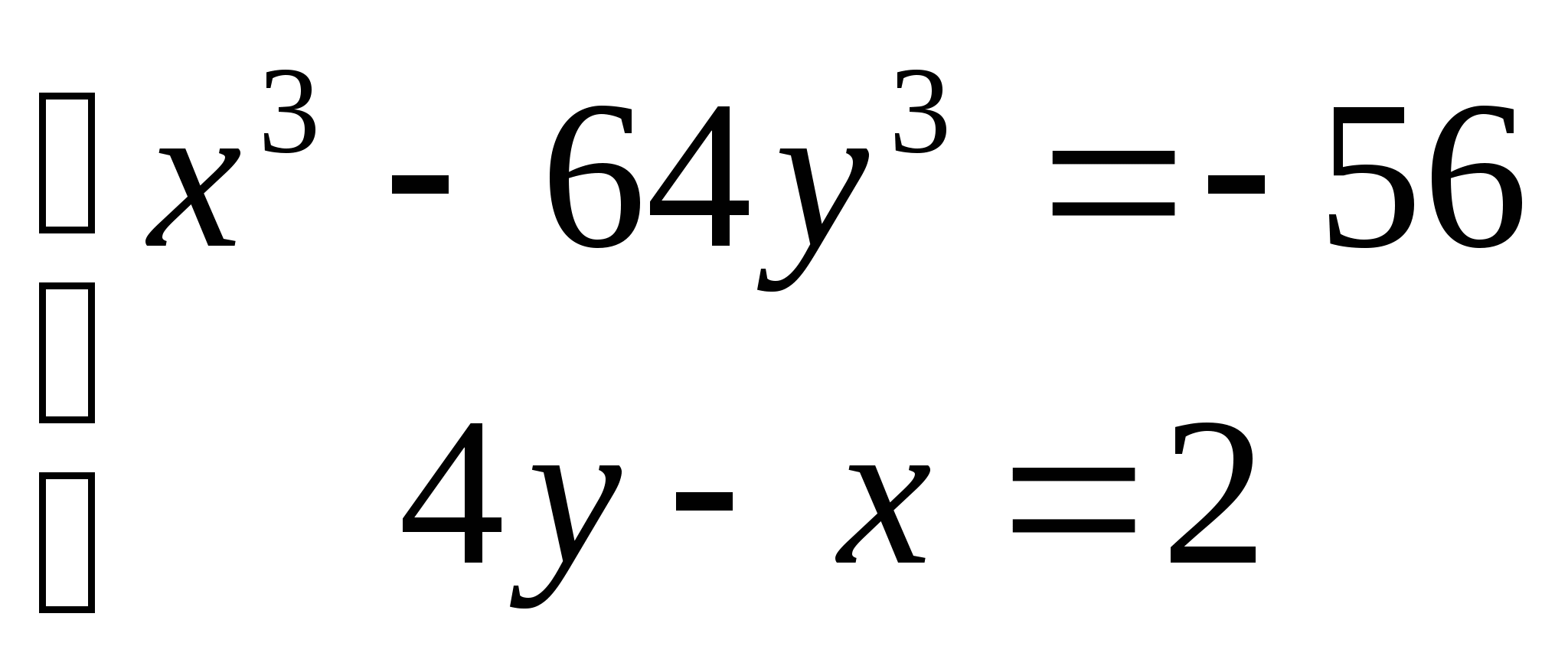 б)
б)
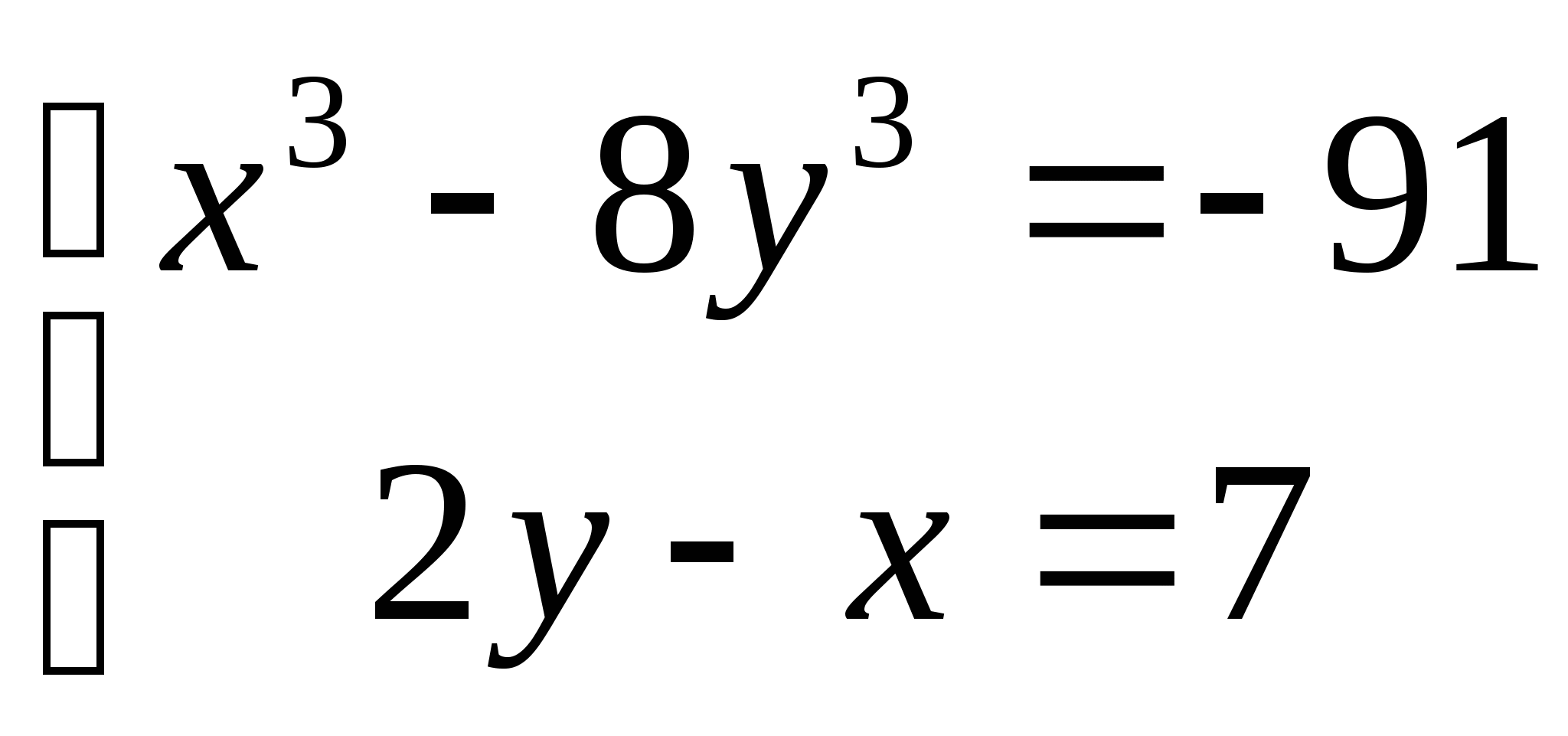
10. а) 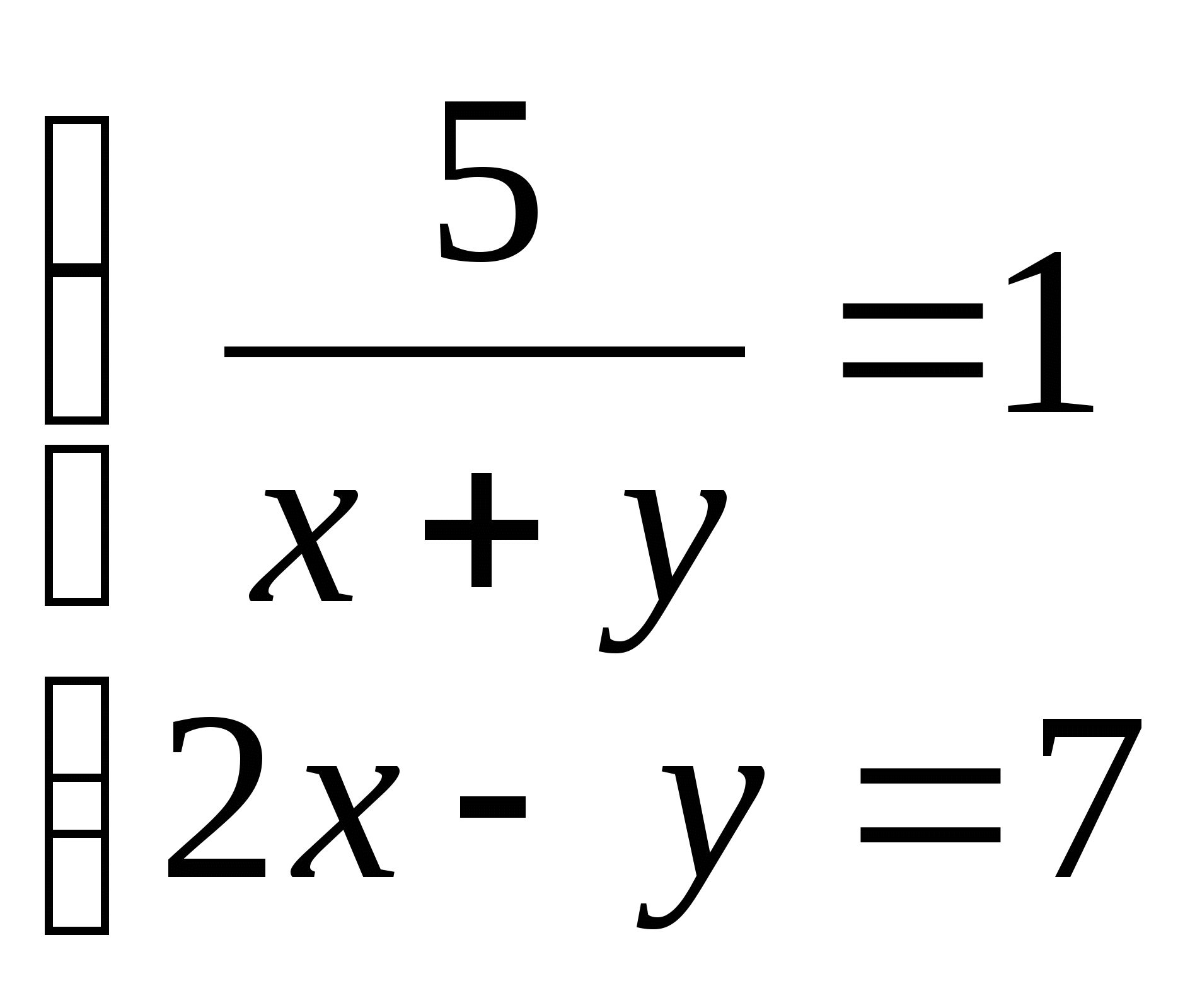 б)
б)
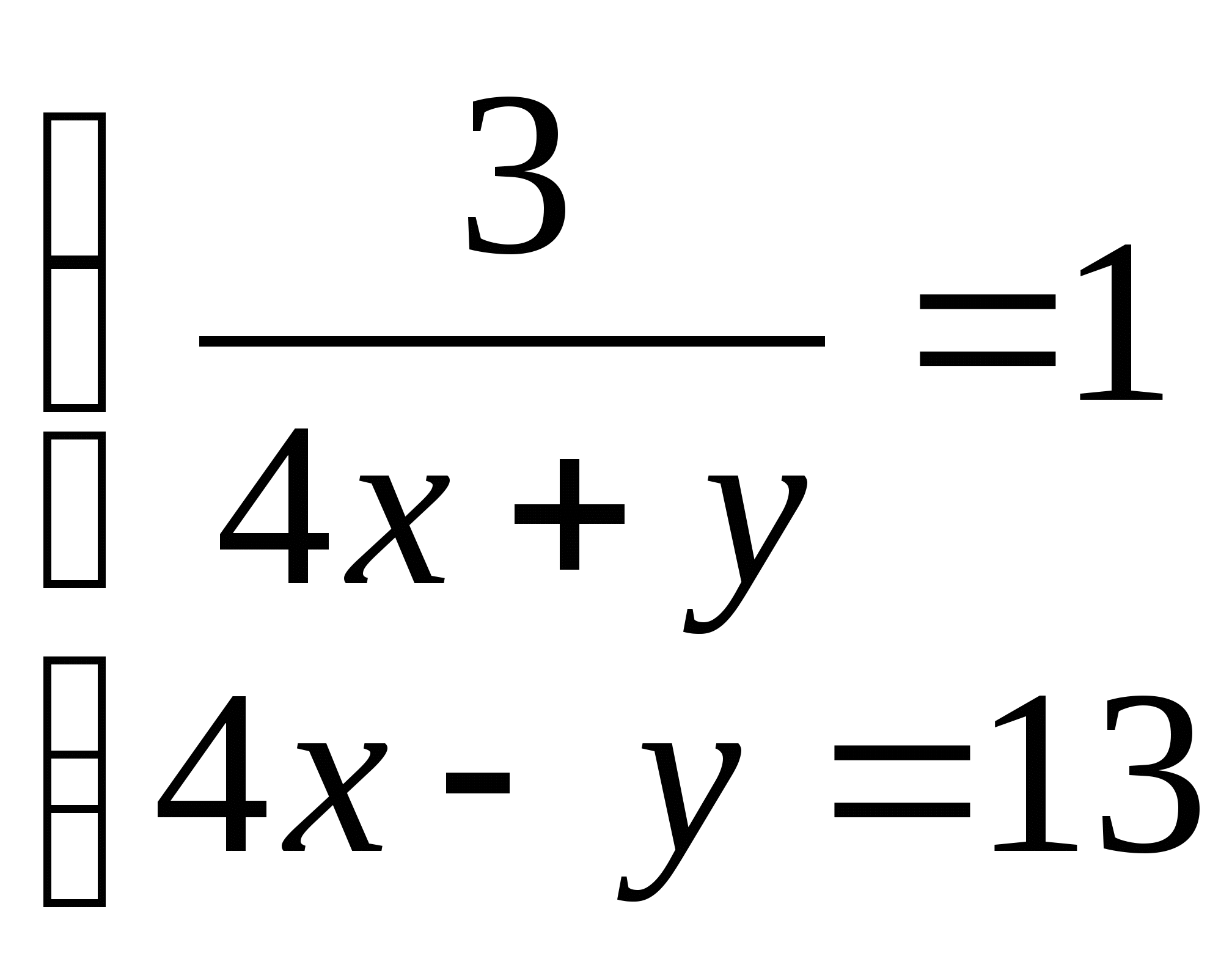
11. а) 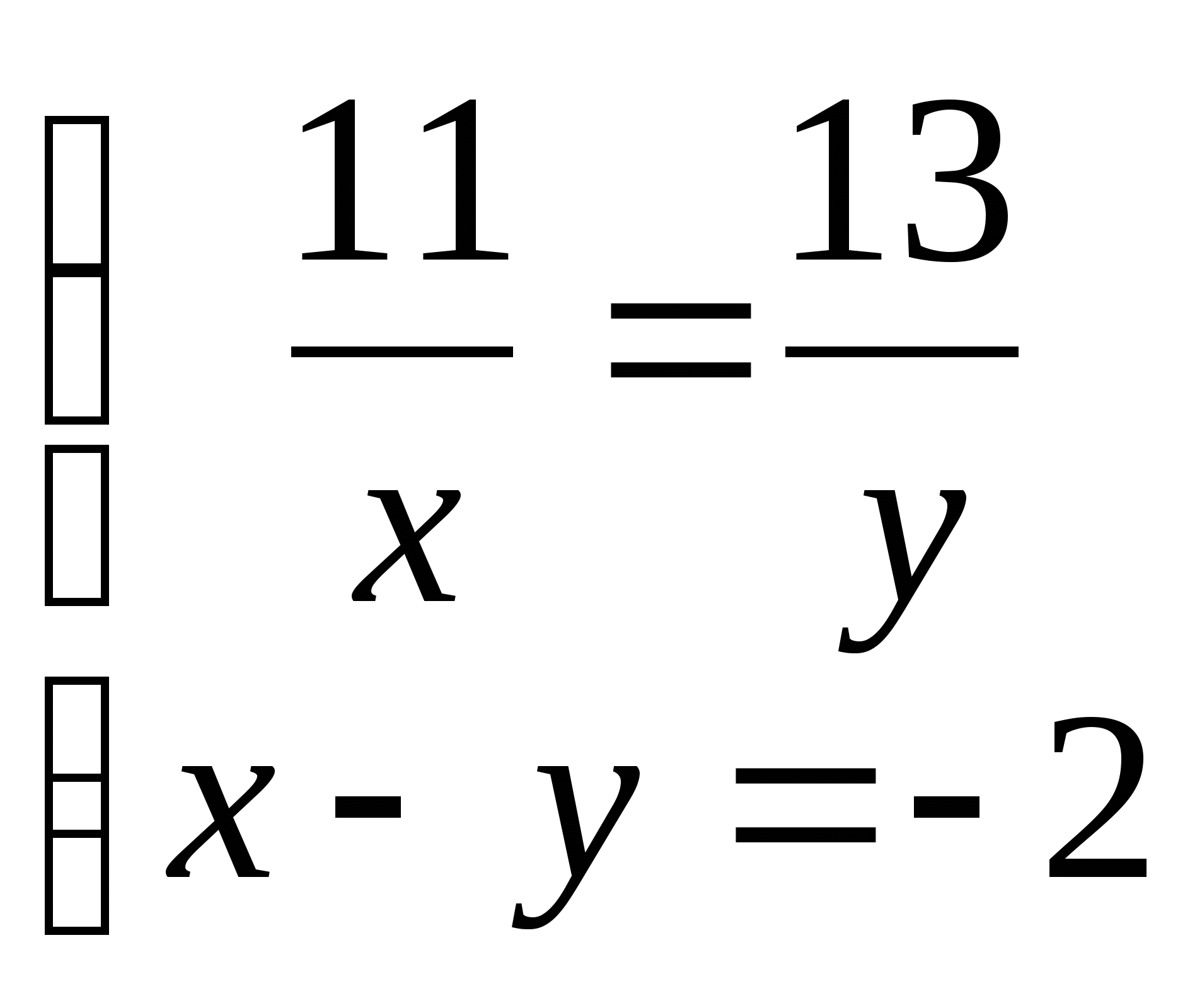 б)
б)
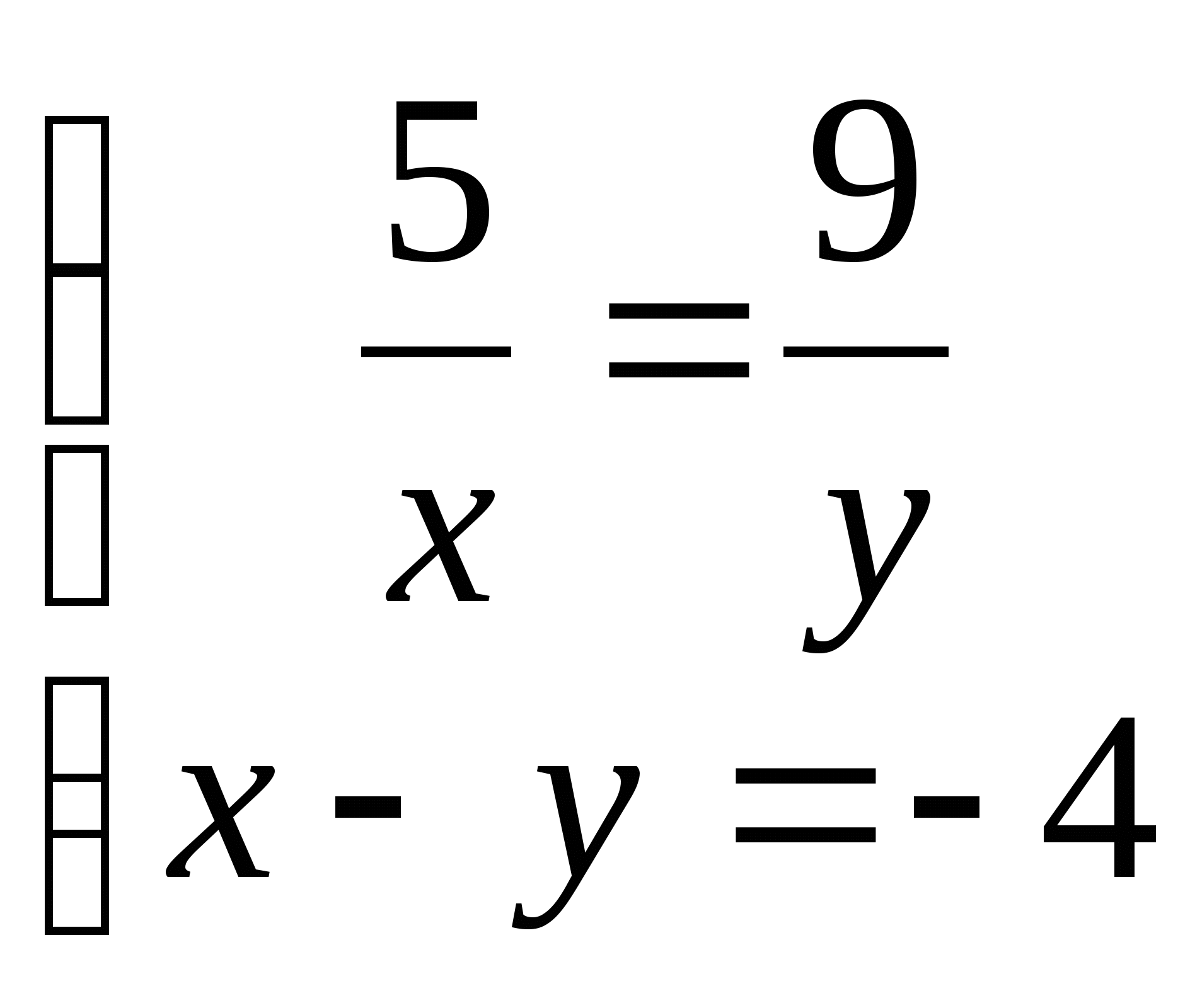
12. а) 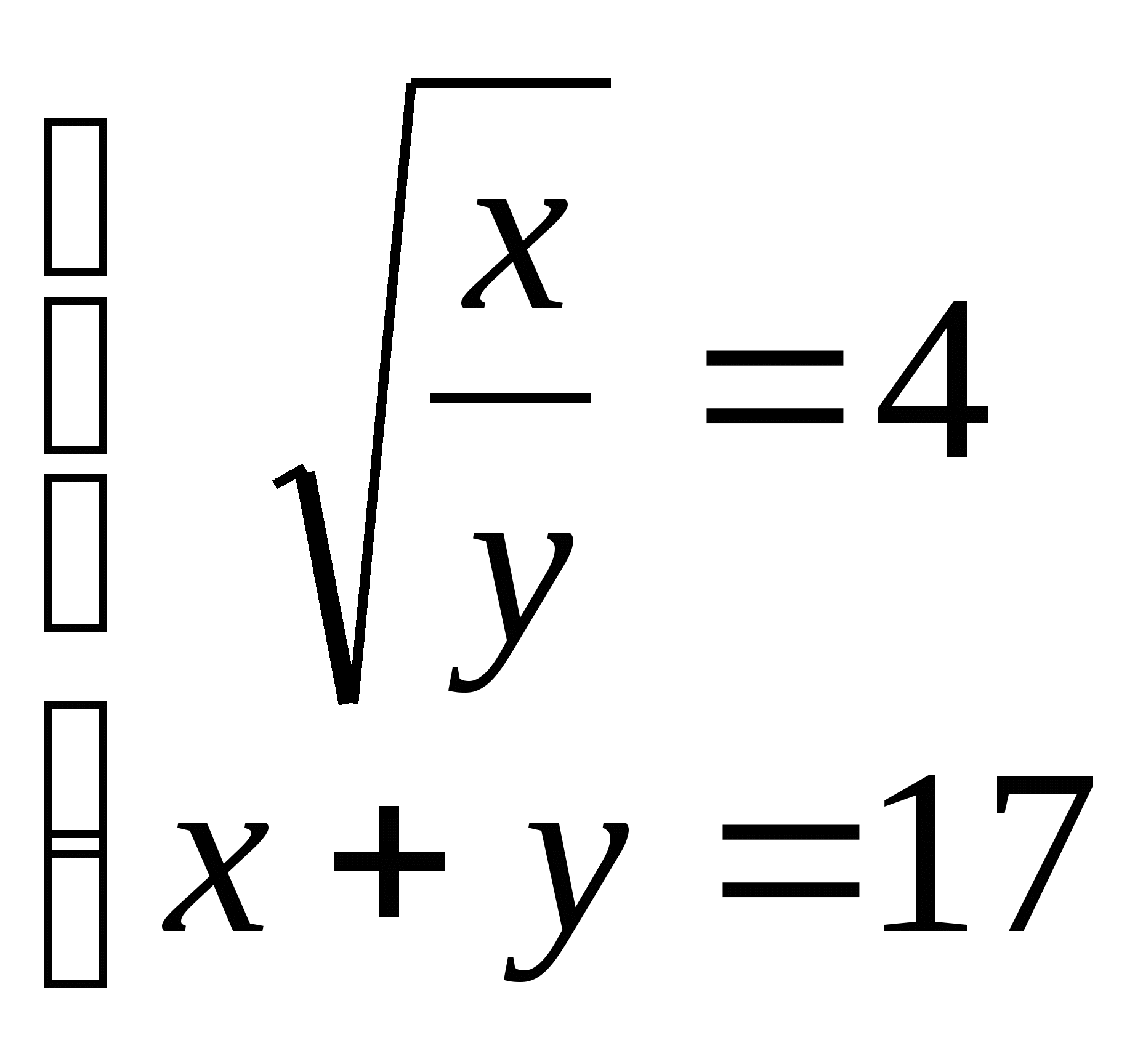 б)
б)
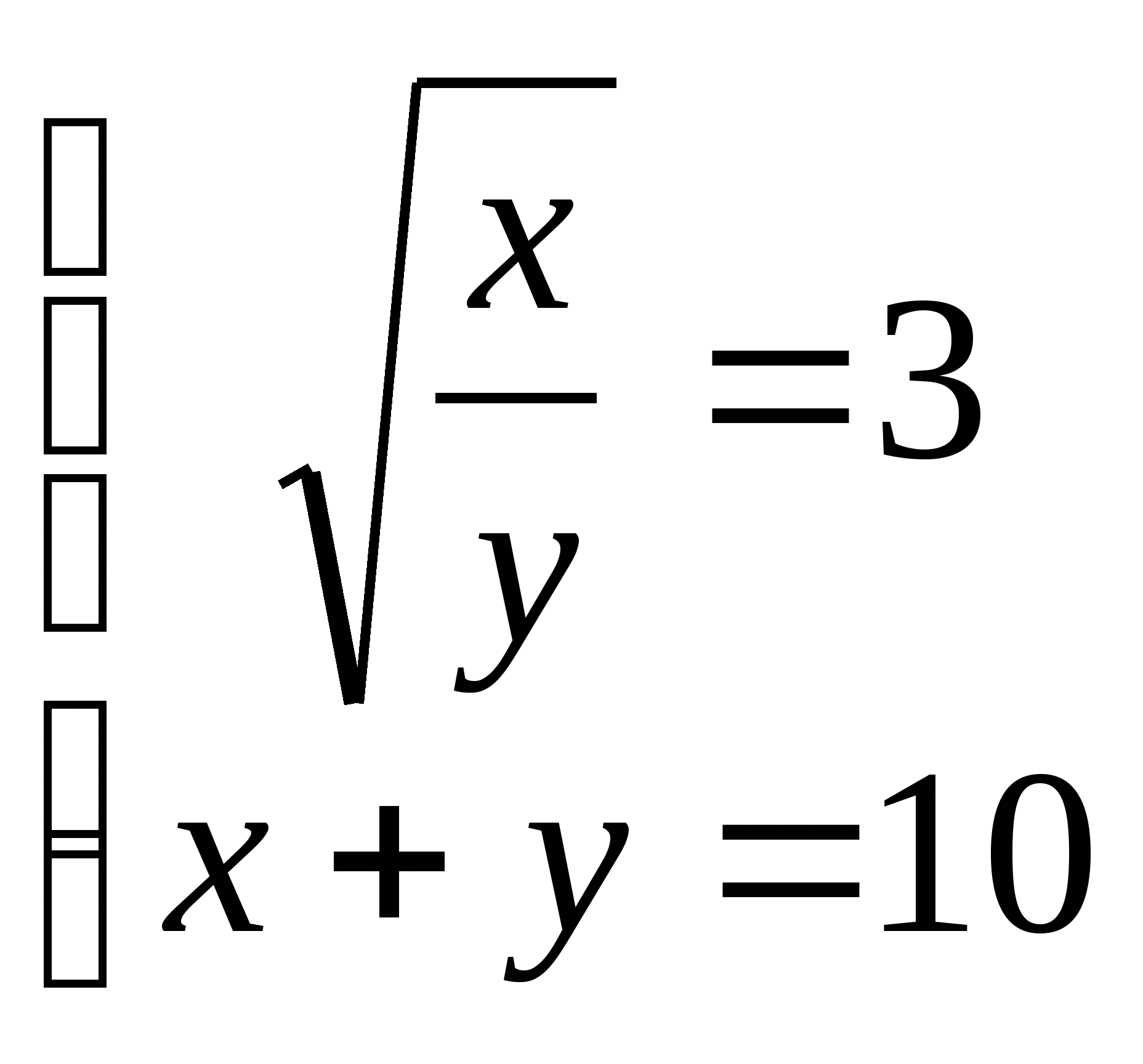
13. а) 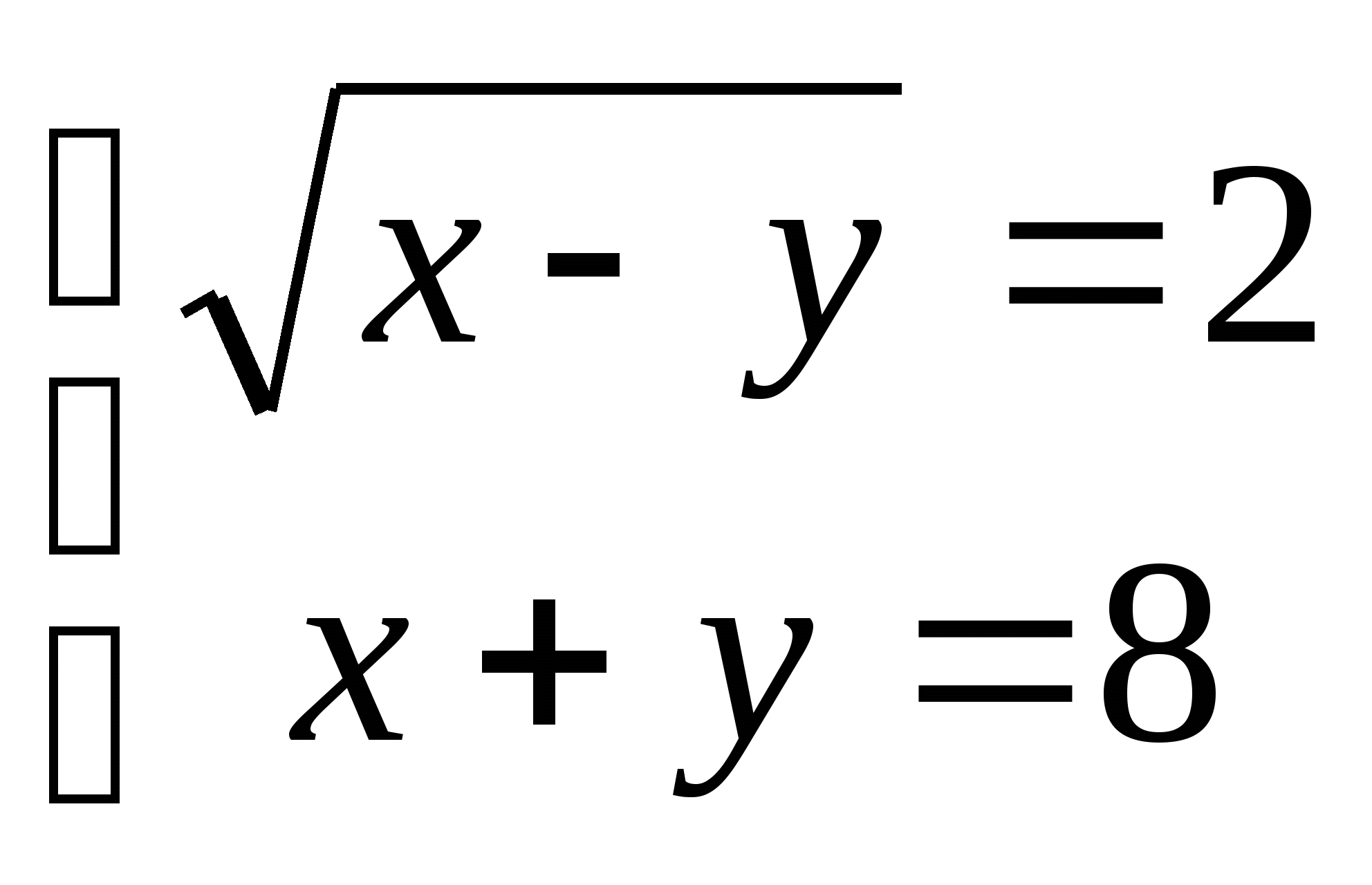 б)
б)
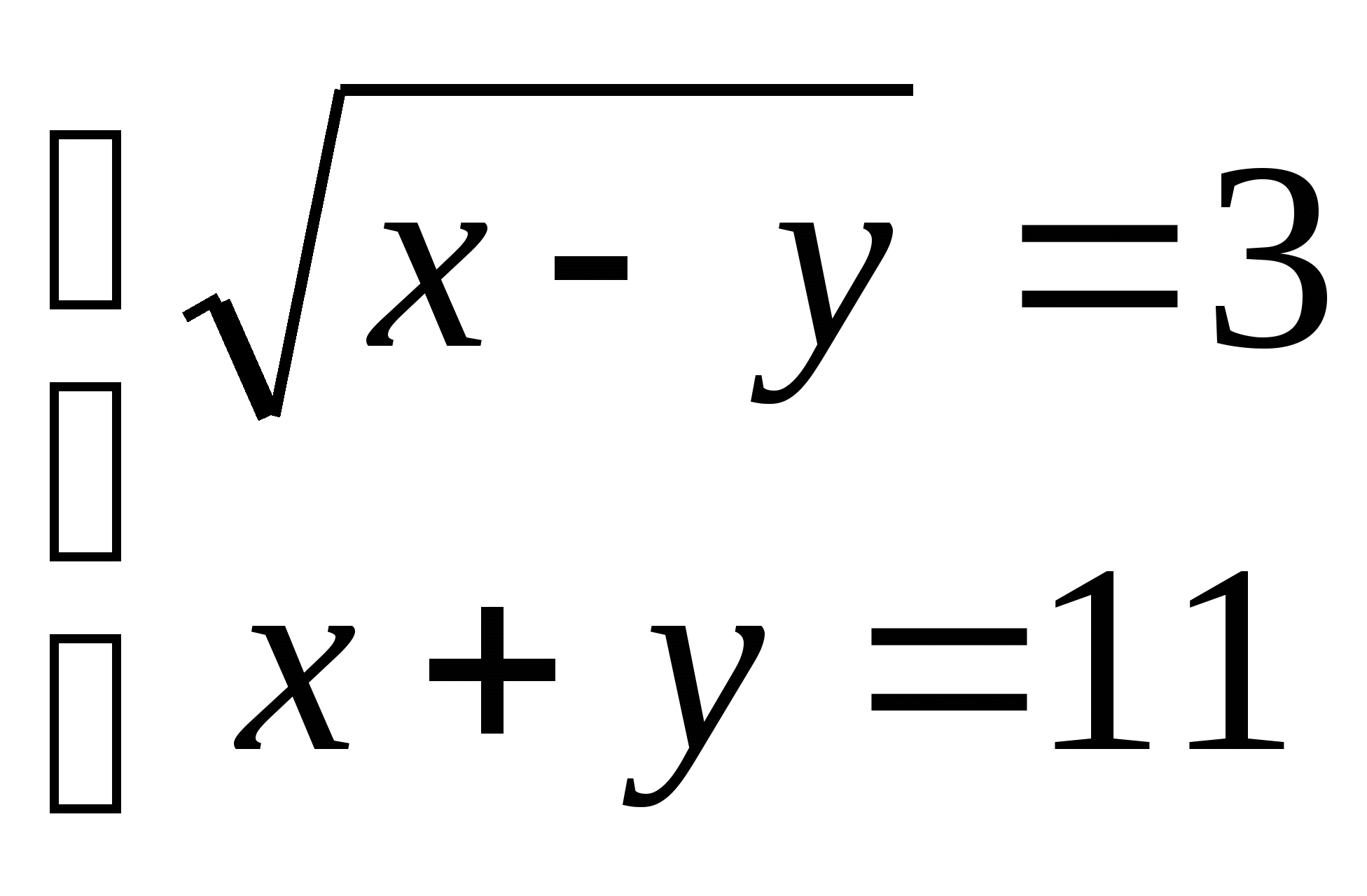
14. а) 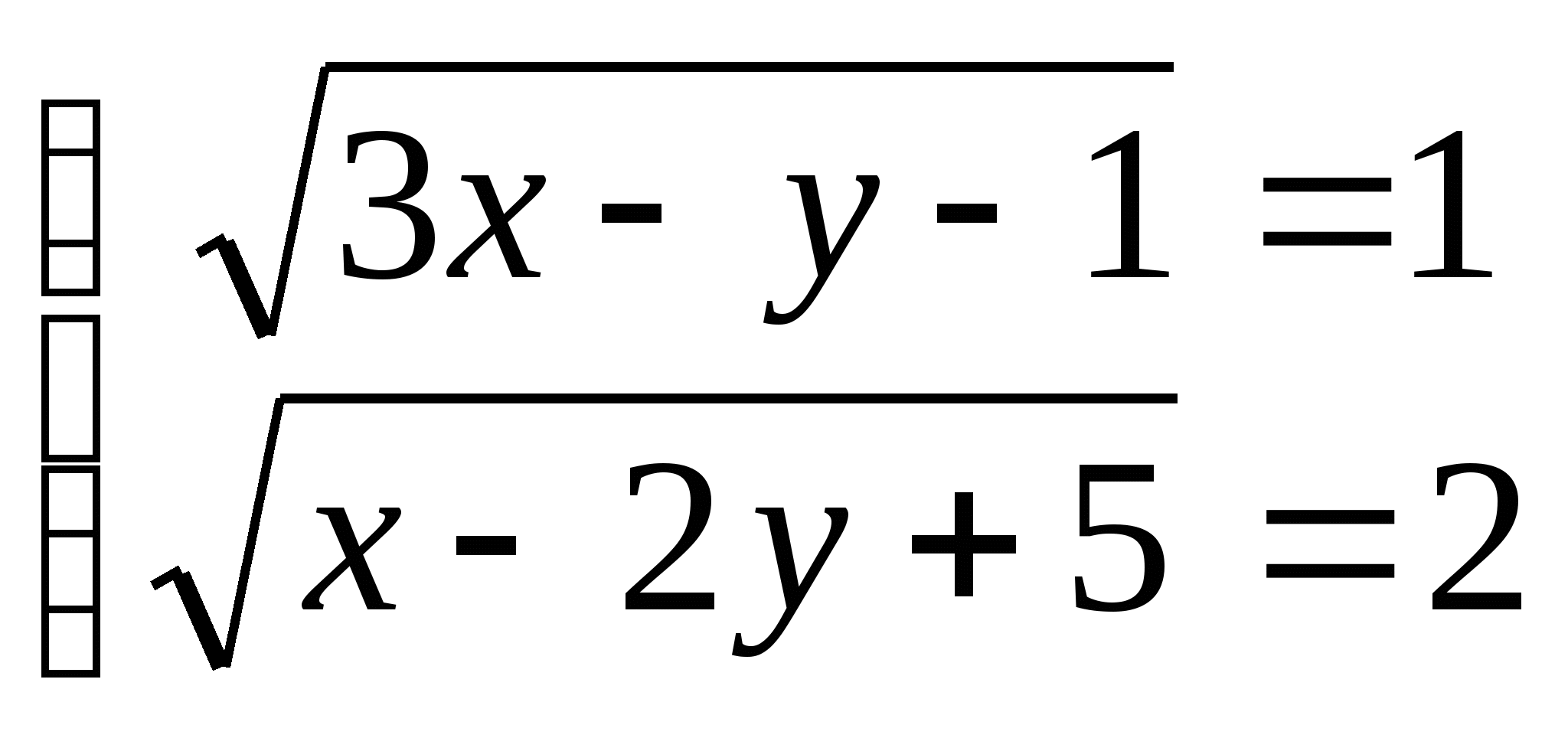 б)
б)
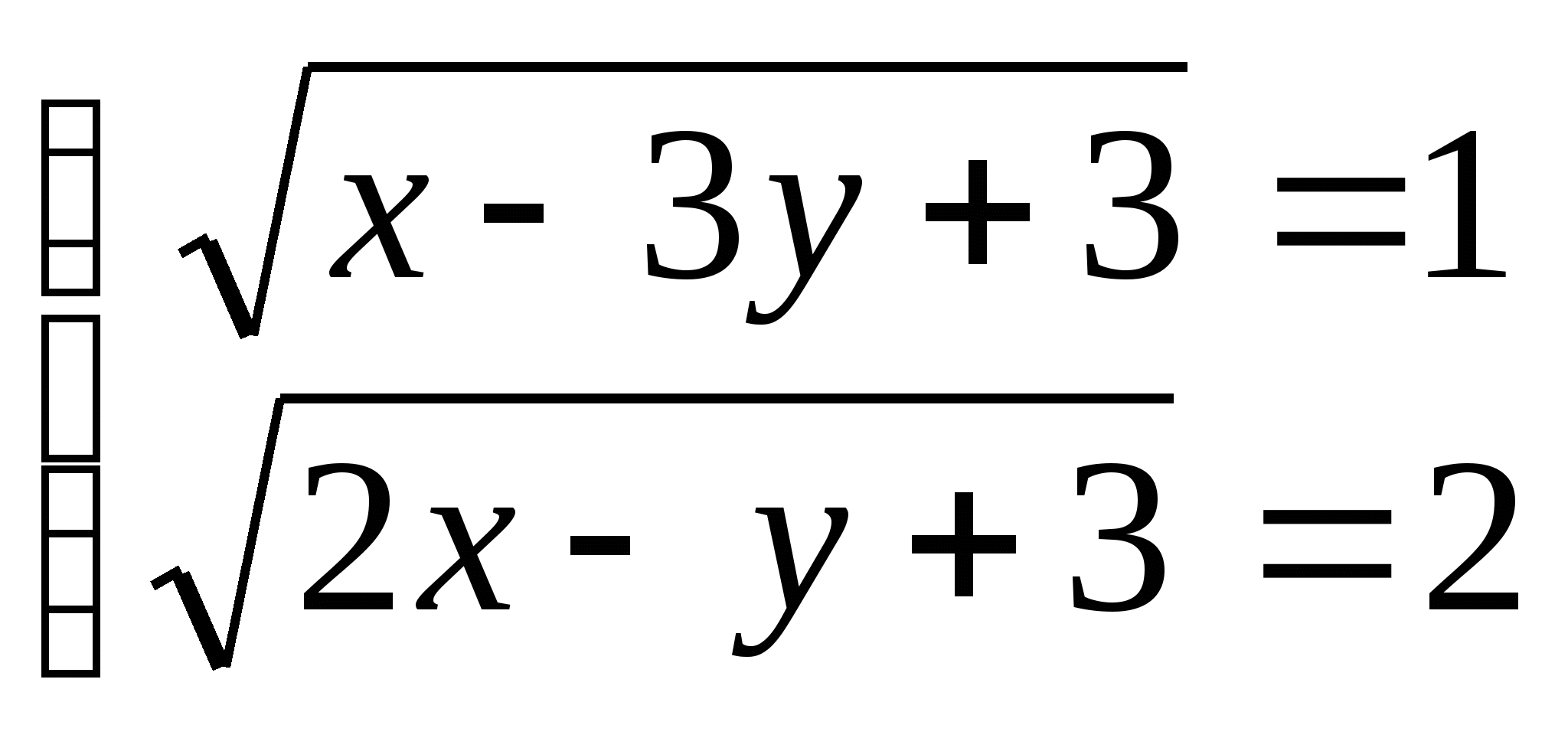
15. а) 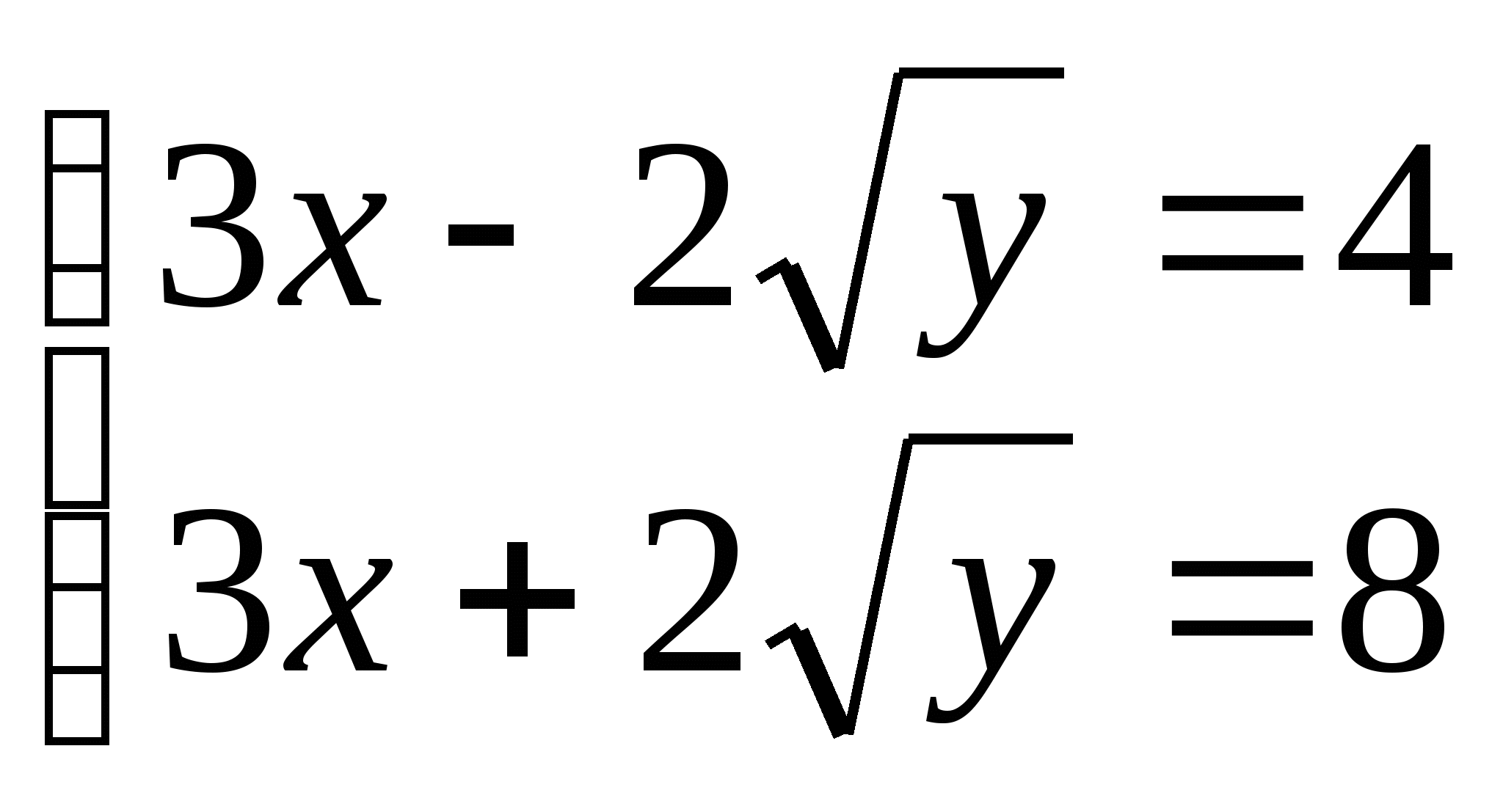 б)
б)
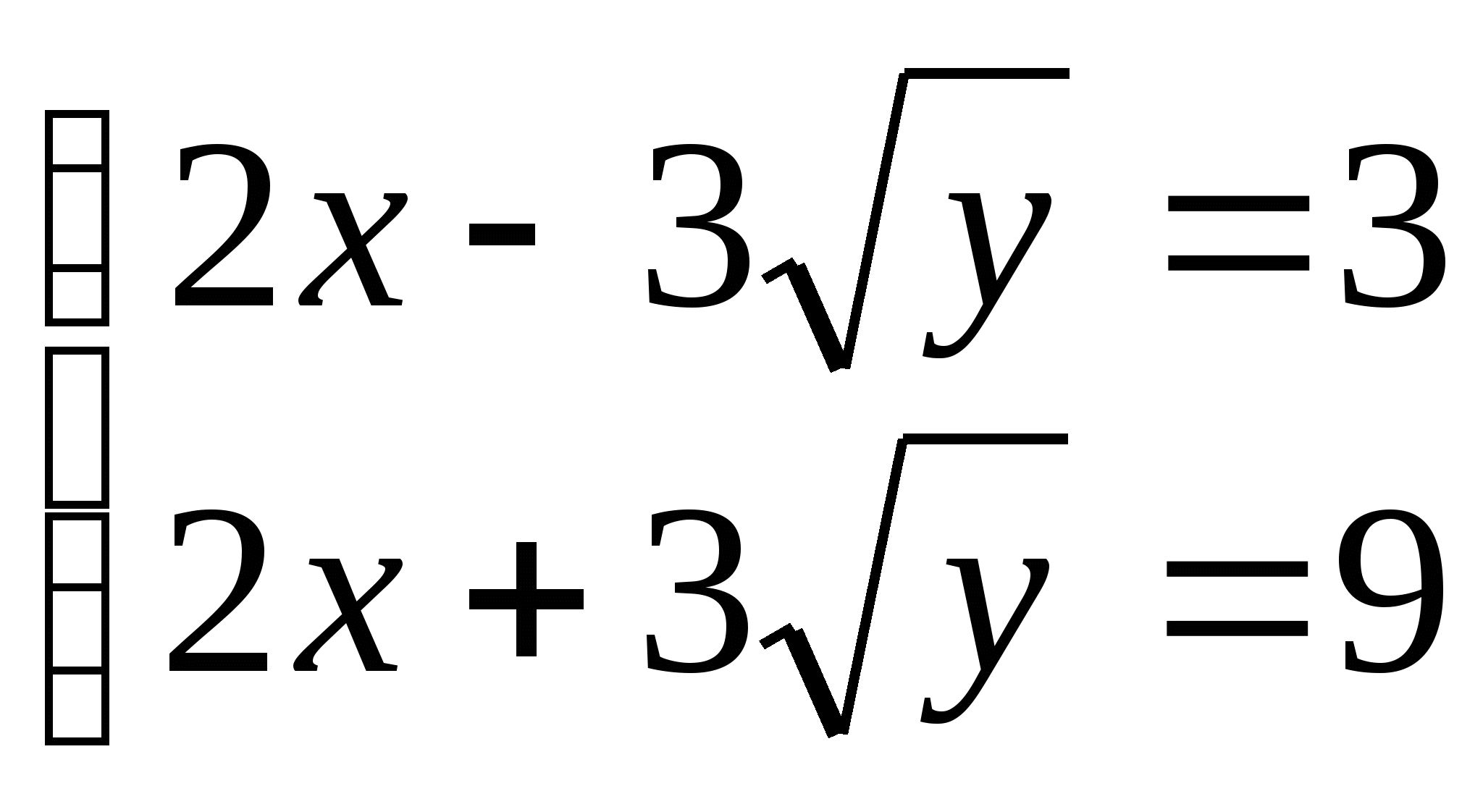
16. а) 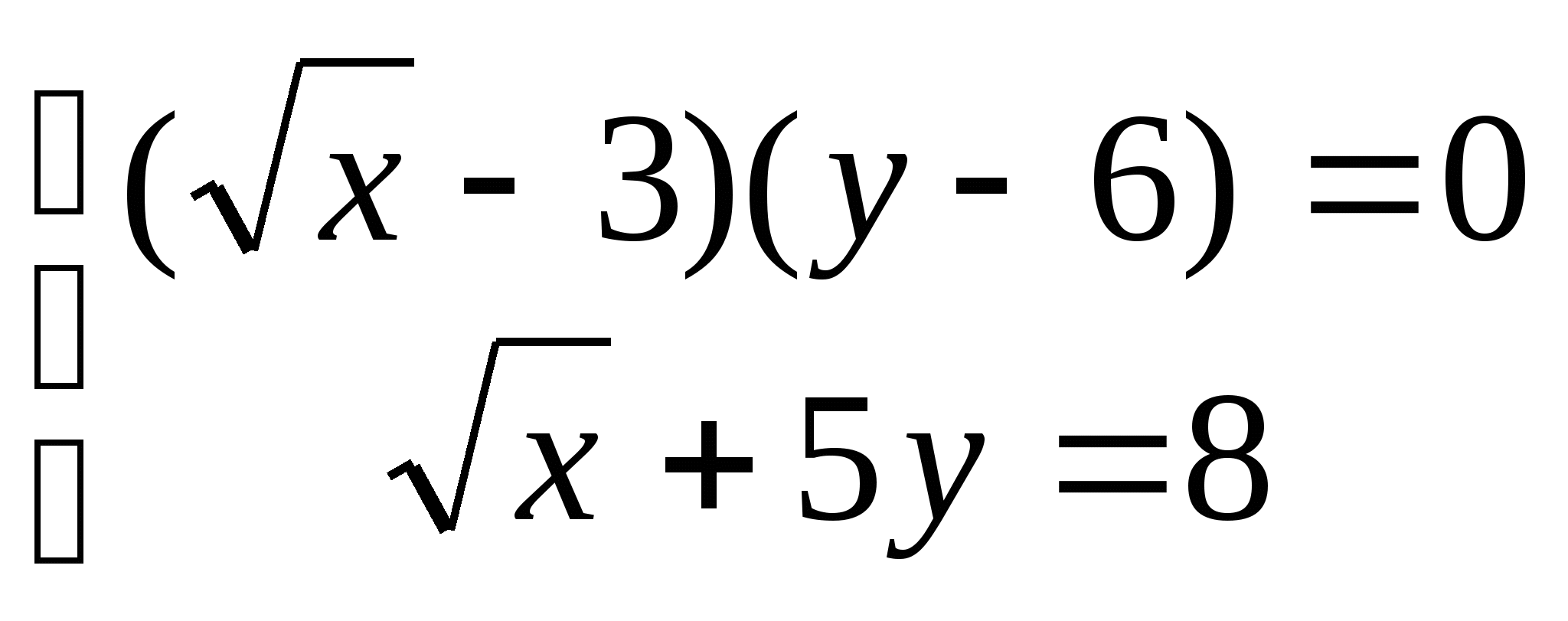 б)
б)
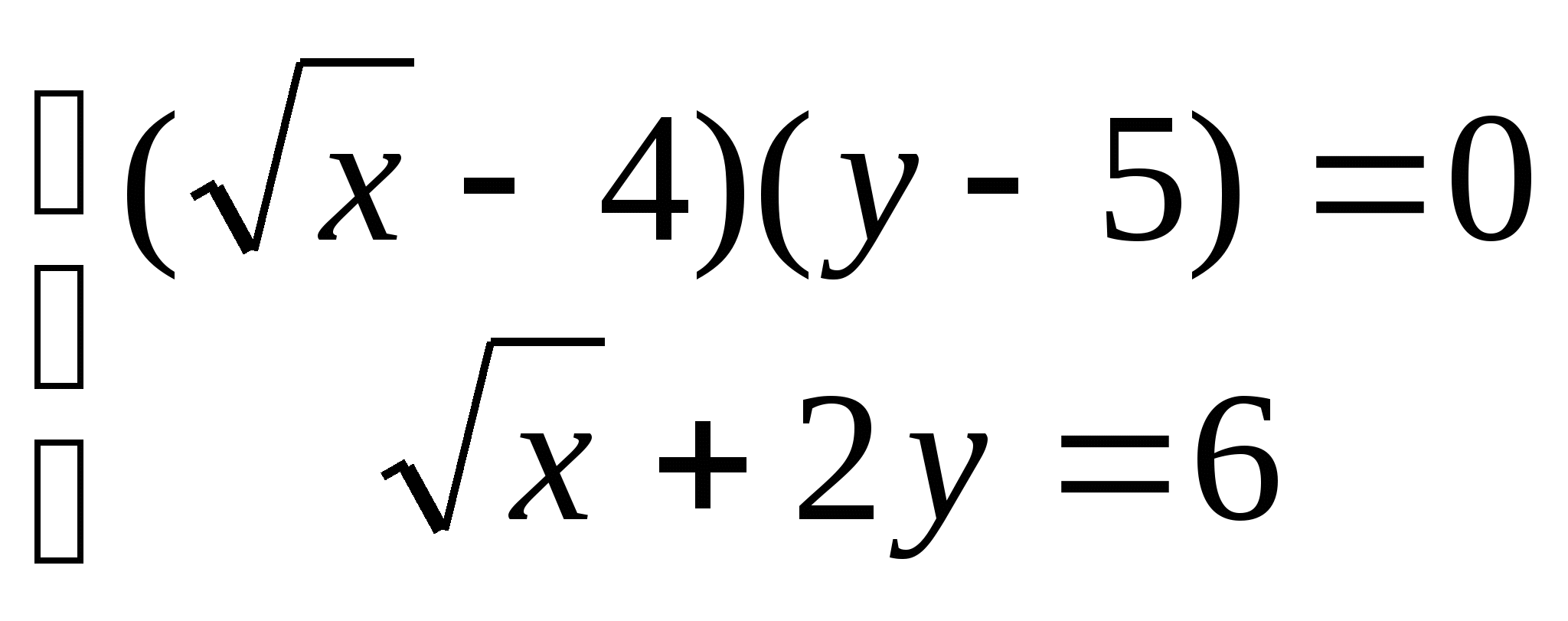
АЛГЕБРАИЧЕСКИЕ ЗАДАЧИ
1. а) Моторная лодка прошла 21 км против течения реки и 8 км по течению, затратив на весь путь 2 ч. Найдите скорость лодки в стоячей воде, если скорость течения реки составляет 1 км/ч.
б) Моторная лодка прошла 24 км против течения реки и 16 км по течению, затратив на весь путь 3 ч. Найдите скорость лодки в стоячей воде, если скорость течения реки составляет 2 км/ч.
2. а) Сколько граммов 3-процентного и сколько граммов 8-процентного раствора соли нужно взять, чтобы получить 260 г 5-процентного раствора?
б) Сколько килограммов 25-процентного и сколько граммов 50-процентного сплавов меди нужно взять, чтобы получить 20 кг 40-процентного сплава?
3. а) Двое рабочих, работая вместе, выполнили задание за 12 часов. За сколько часов может выполнить это задание каждый рабочий самостоятельно, если один из них может это сделать на 7 ч быстрее другого?
б) Две бригады, работая вместе, вспахали поле за 8 ч. За сколько часов может вспахать поле каждая бригада, работая самостоятельно, если второй бригаде на это нужно на 12 ч больше, чем первой?
4. а) Тракторист должен был за определенное время вспахать поле площадью 180 га. Ежедневно он вспахивал на 2 га больше, чем планировал, и закончил работу на 1 день раньше срока. За сколько дней тракторист вспахал поле?
б) Рабочий должен был за определенное время изготовить 160 деталей. Ежедневно он изготовлял на 4 детали больше, чем планировал, и закончил работу на 2 день раньше срока. За сколько дней он выполнил работу?
5. а) Из одного города в другой, расстояние между которыми равно 300 км, выехали одновременно две машины. Одна из них двигалась со скоростью на 10 км/ч больше, чем вторая, а потому прибыла в пункт назначения на 1 ч раньше второй. Найдите скорость каждой машины.
б) Из одного города в другой, расстояние между которыми равно 240 км, выехали одновременно автобус и автомобиль. Автобус двигался со скоростью на 20 км/ч меньше, чем автомобиль, а потому прибыл в пункт назначения на 1 ч позже. Найдите скорость каждой машины.
6. а) Вкладчик положил в банк 1200 гривен на два различных счета. По первому из них банк выплачивает 6% годовых, а по второму - 8% годовых. Через год вкладчик получил 80 гривен процентных денег. Сколько гривен он положил на каждый счет?
б) Вкладчик положил в банк 1500 гривен на два различных счета. По первому из них банк выплачивает 7% годовых, а по второму - 10% годовых. Через год вкладчик получил 120 гривен процентных денег. Сколько гривен он положил на каждый счет?
7. а) Из города А в город В выехал велосипедист. Через 3 ч из города А выехал мотоциклист, который прибыл в город В одновременно с велосипедистом. Найдите скорость мотоциклиста, если она на 45 км/ч больше скорости велосипедиста, а расстояние между городами 60 км.
б) Из города А в город В вышел товарный поезд. Через 2 ч из города А вышел пассажирский поезд, который прибыл в город В одновременно с товарным. Найдите скорость товарного поезда, если она на 20 км/ч меньше скорости пассажирского, а расстояние между городами 350 км.
НЕРАВЕНСТВА
1.Решить неравенство
а) ![]() б)
б)
![]()
2. а) ![]() б)
б)
![]()
3. а) ![]() б)
б)
![]()
4. а) ![]() б)
б)
![]()
5.а) ![]() б)
б)
![]()
6. а) ![]() б)
б)
![]()
7. а) ![]() б)
б)
![]()
8. а) ![]() б)
б)
![]()
9. а) ![]() б)
б)
![]()
10. а) ![]() б)
б)
![]()
11. а) ![]() б)
б)
![]()
12. а) ![]() б)
б)
![]()
13. а) ![]() б)
б)
![]()
14. а) ![]() б)
б)
![]()
15. а) ![]() б)
б)
![]()
16. а) ![]() б)
б)
![]()
17. а) ![]() б)
б)
![]()
18. а) ![]() б)
б)
![]()
19. а) ![]() б)
б)
![]()
СИСТЕМЫ НЕРАВЕНСТВ
1.Решить систему неравенств
а) ![]() б)
б)
![]()
2.а) 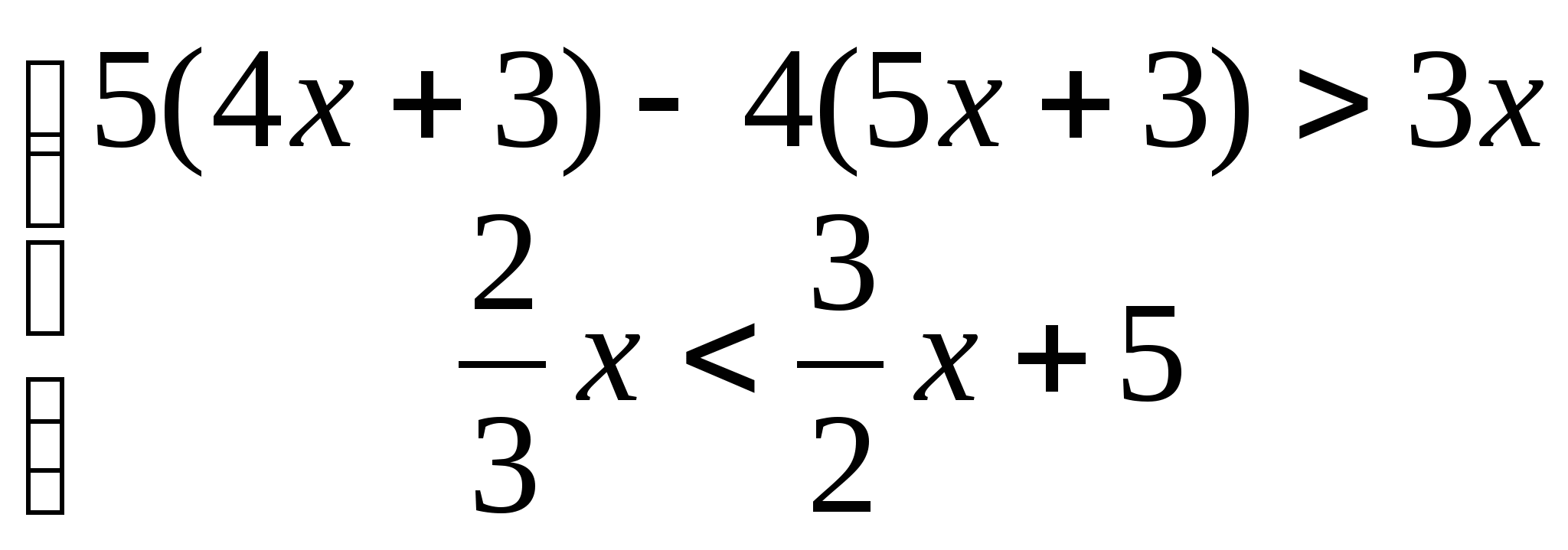 б)
б)
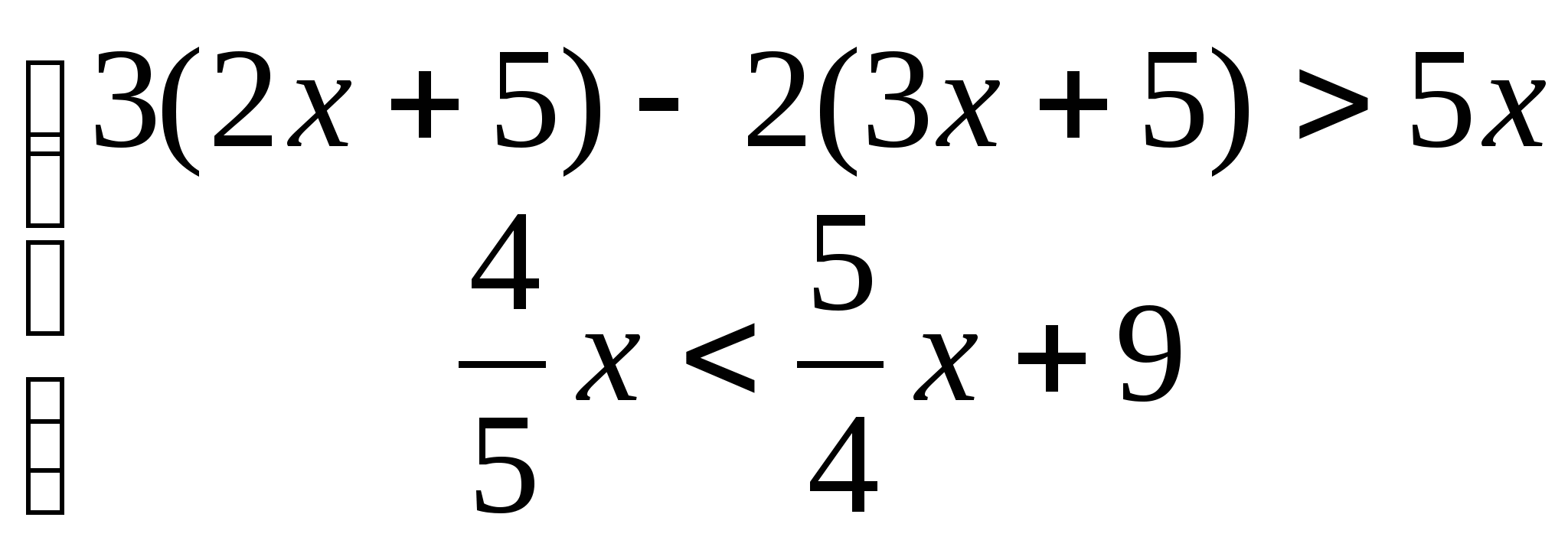
3. а) 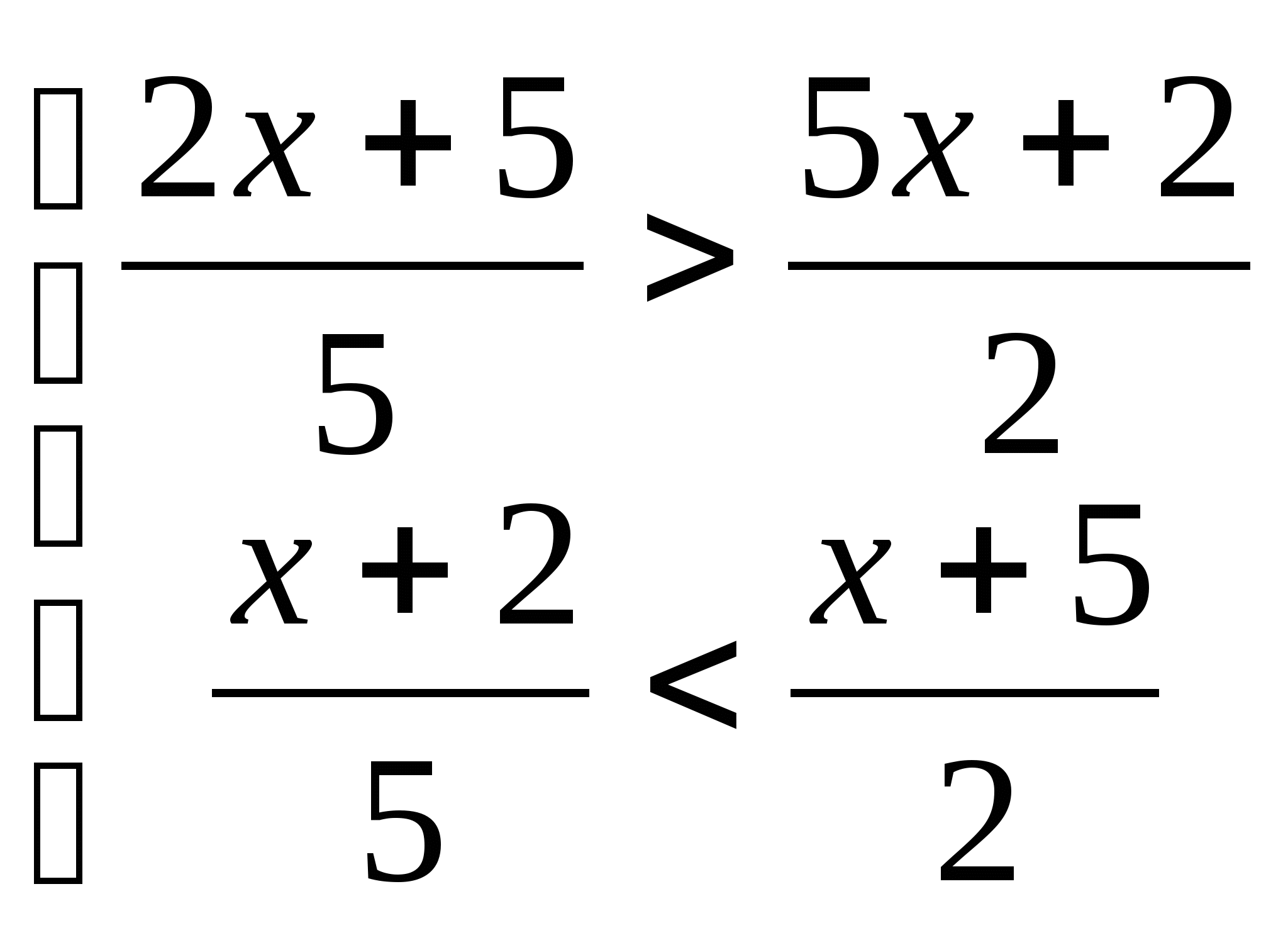 б)
б)
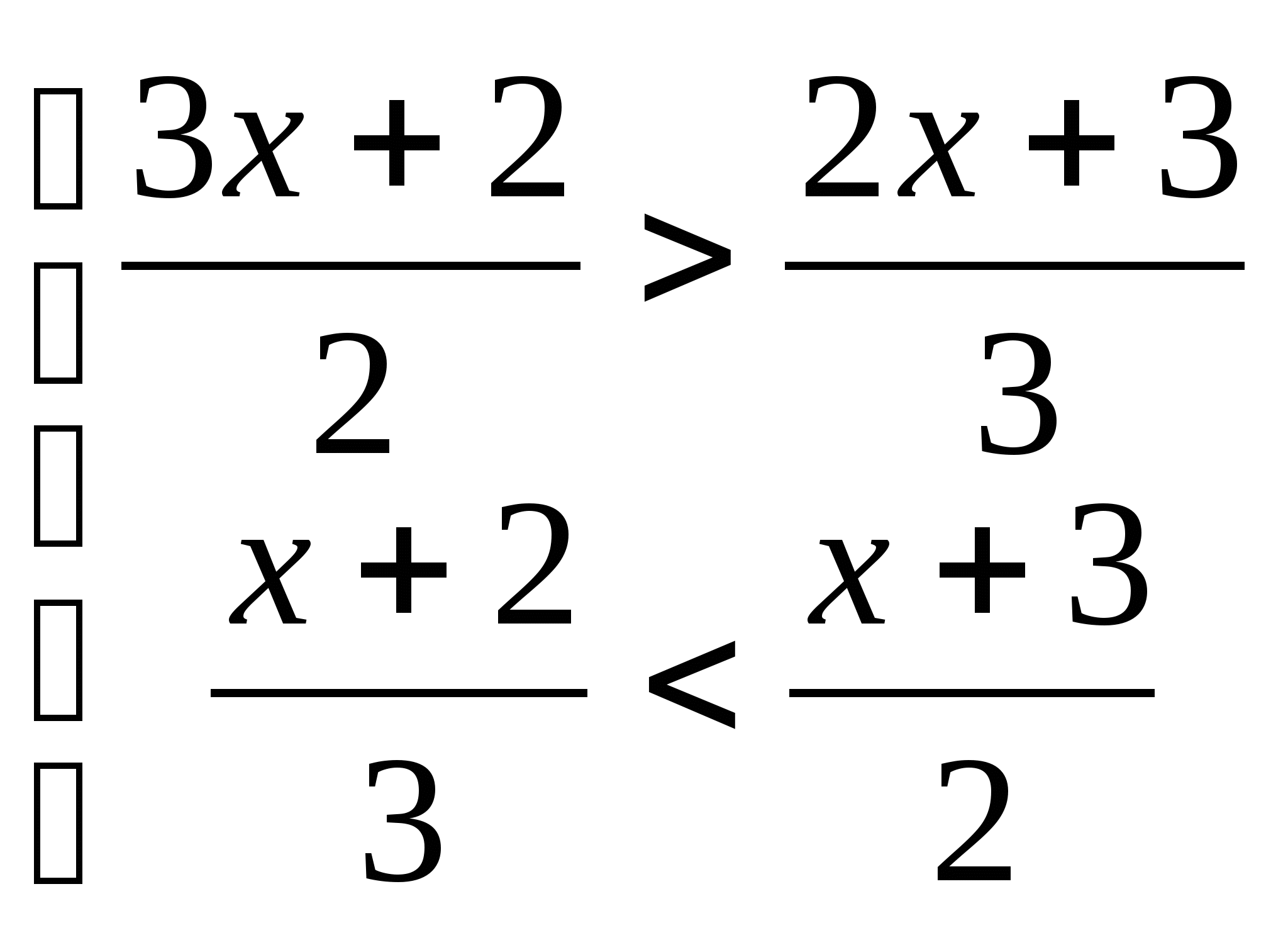
4. а) 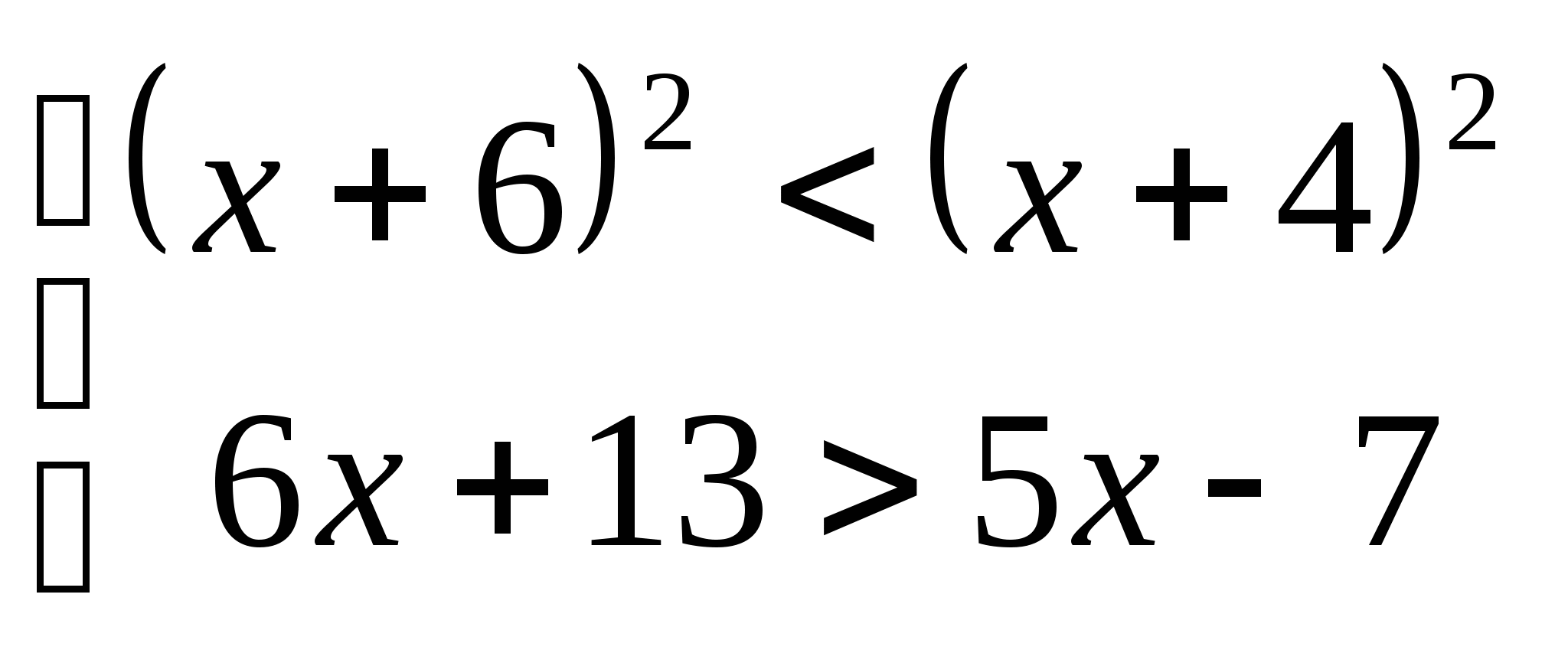 б)
б)
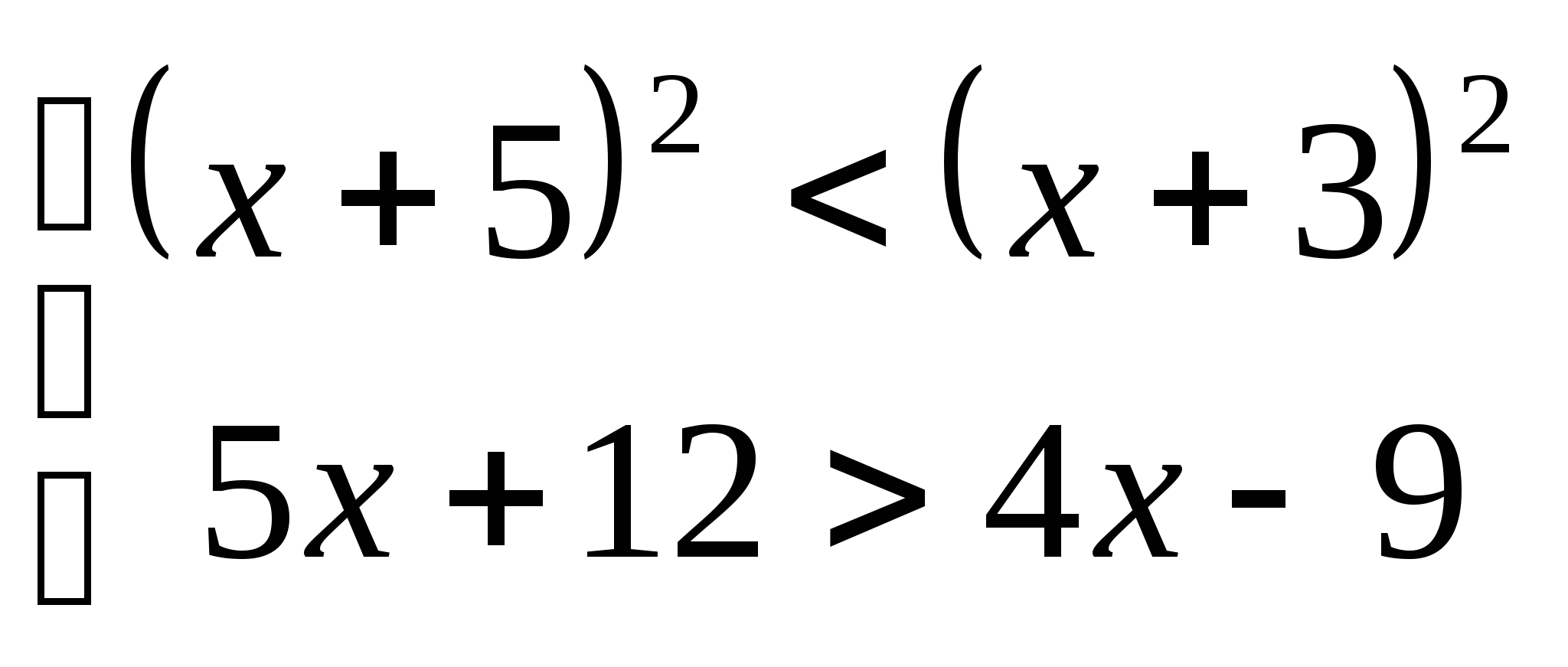
5. а) ![]() б)
б)
![]()
6. а) ![]() б)
б)
![]()
7.![]() б)
б)
![]()
8. а) 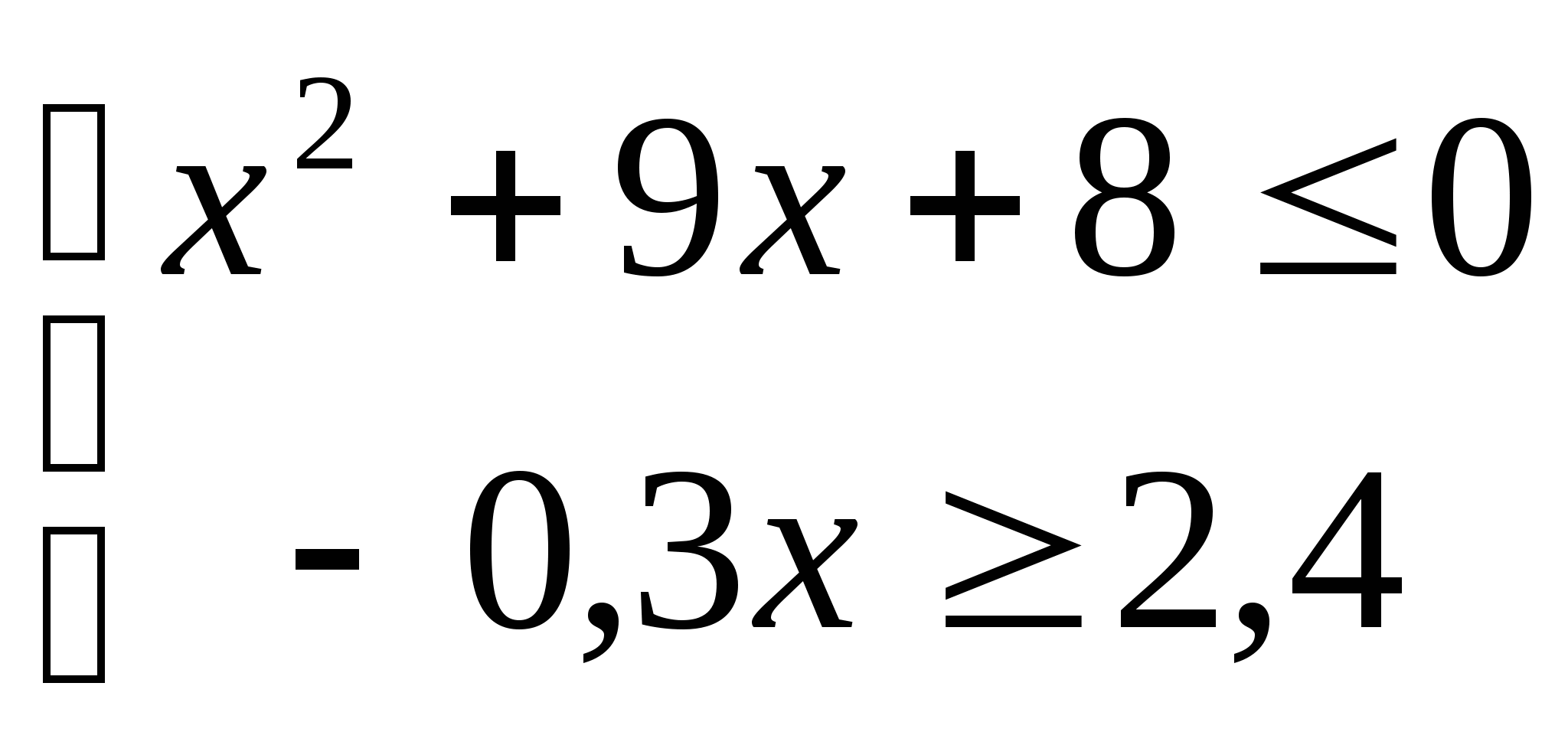 б)
б)
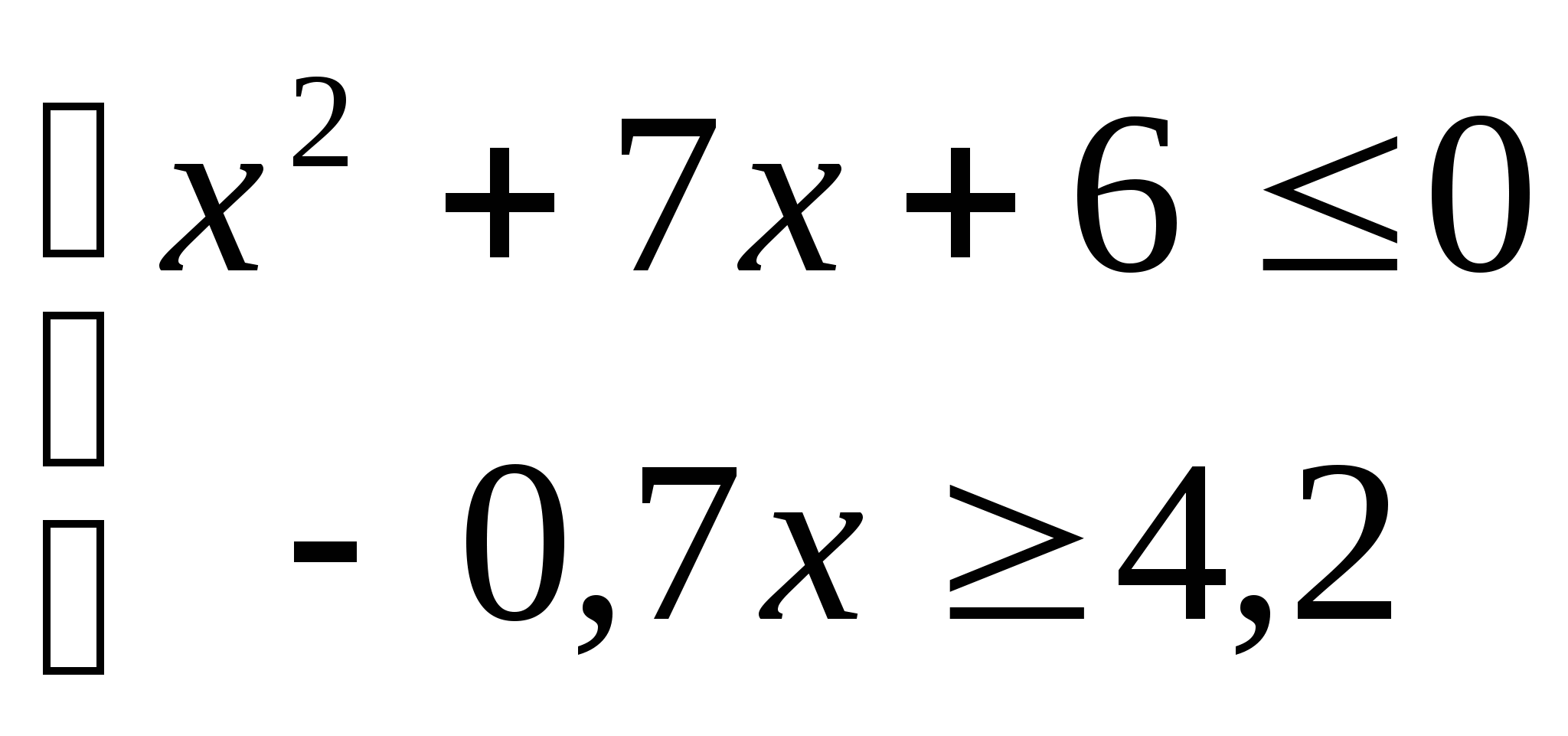
9. а) 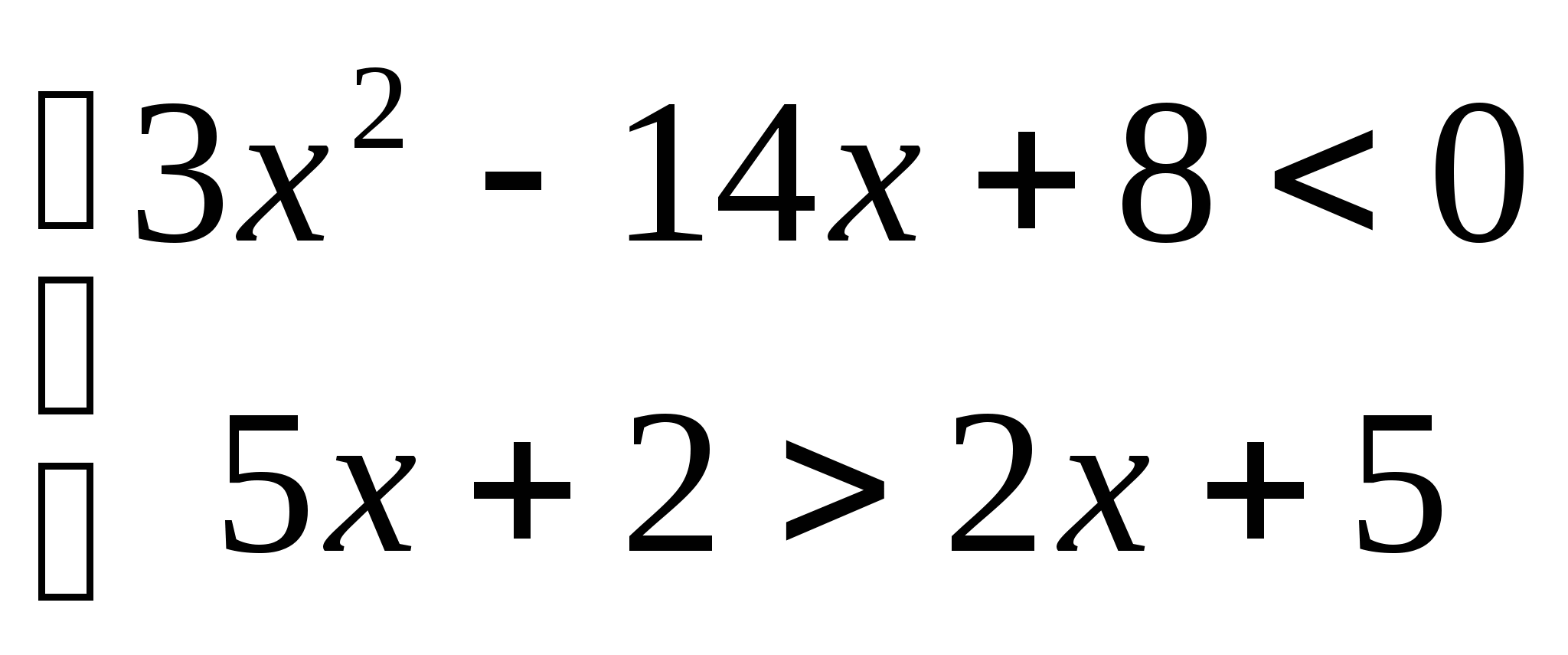 б)
б)
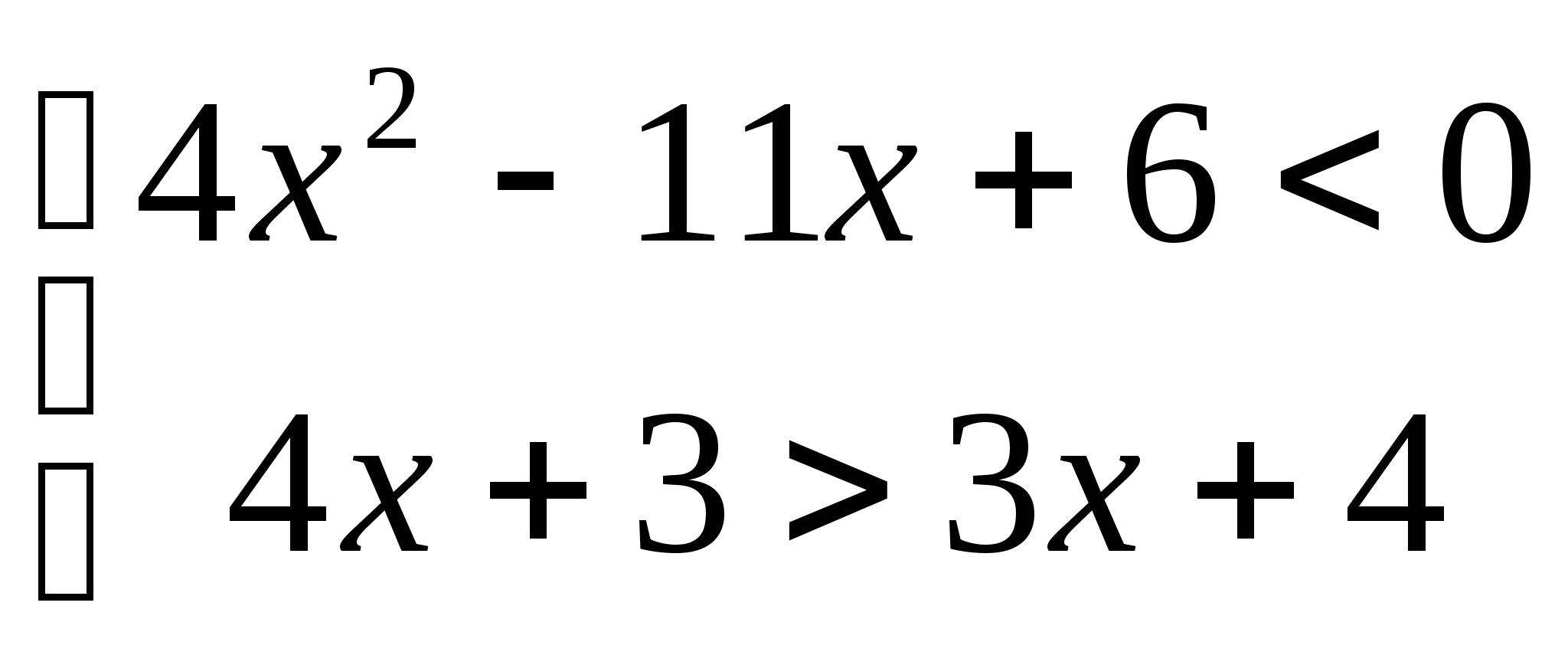
10. а) 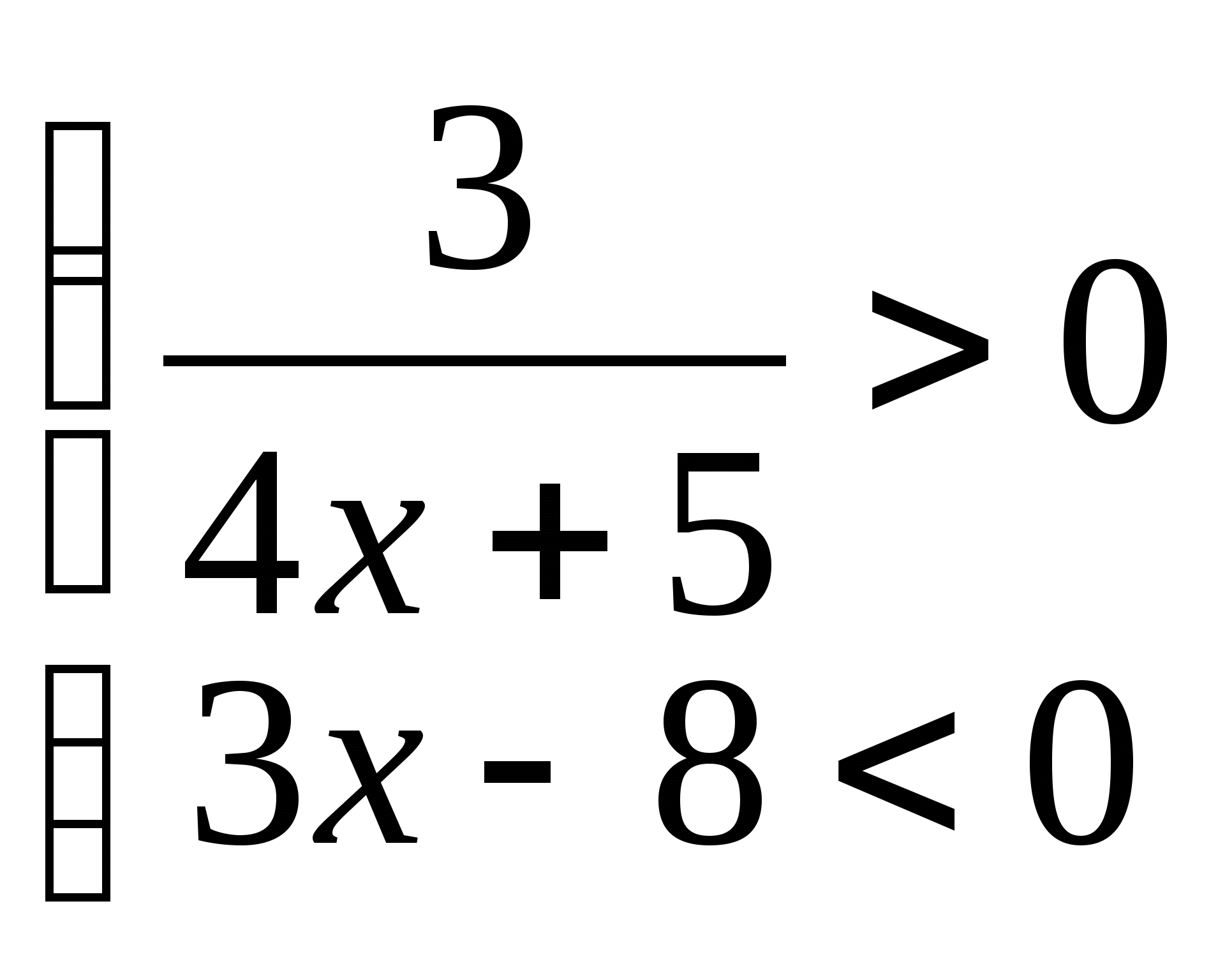 б)
б)
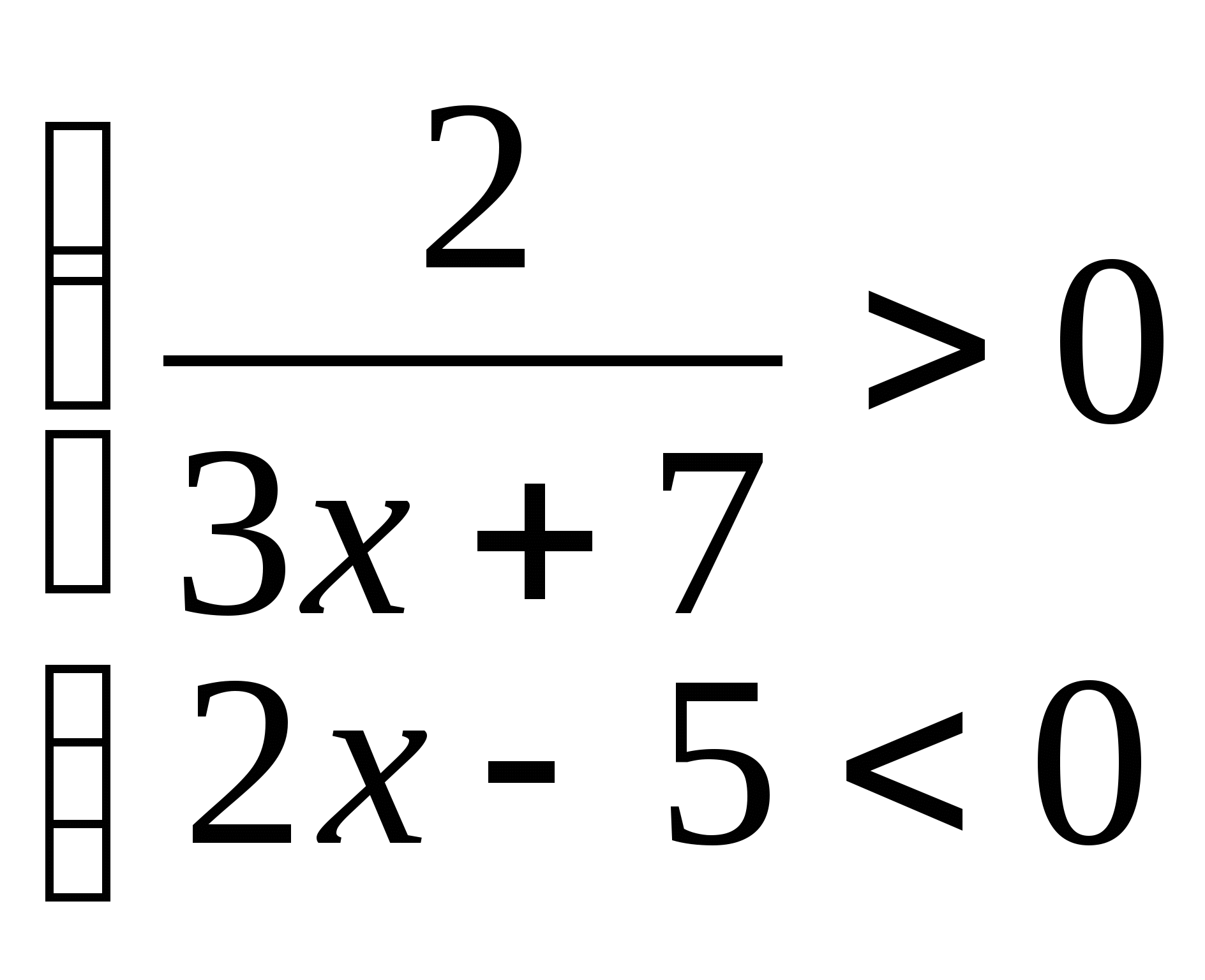
11. а) 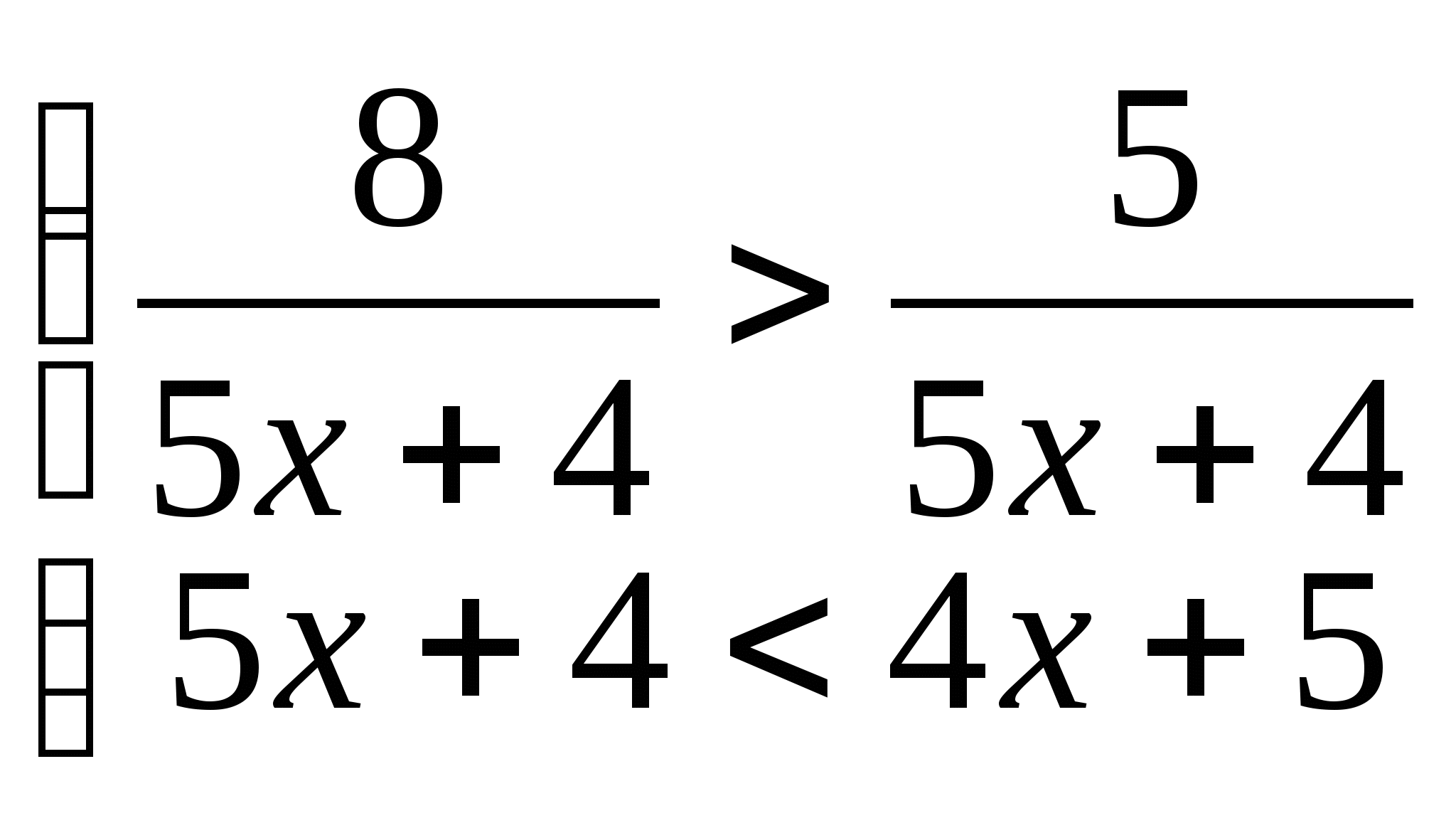 б)
б)
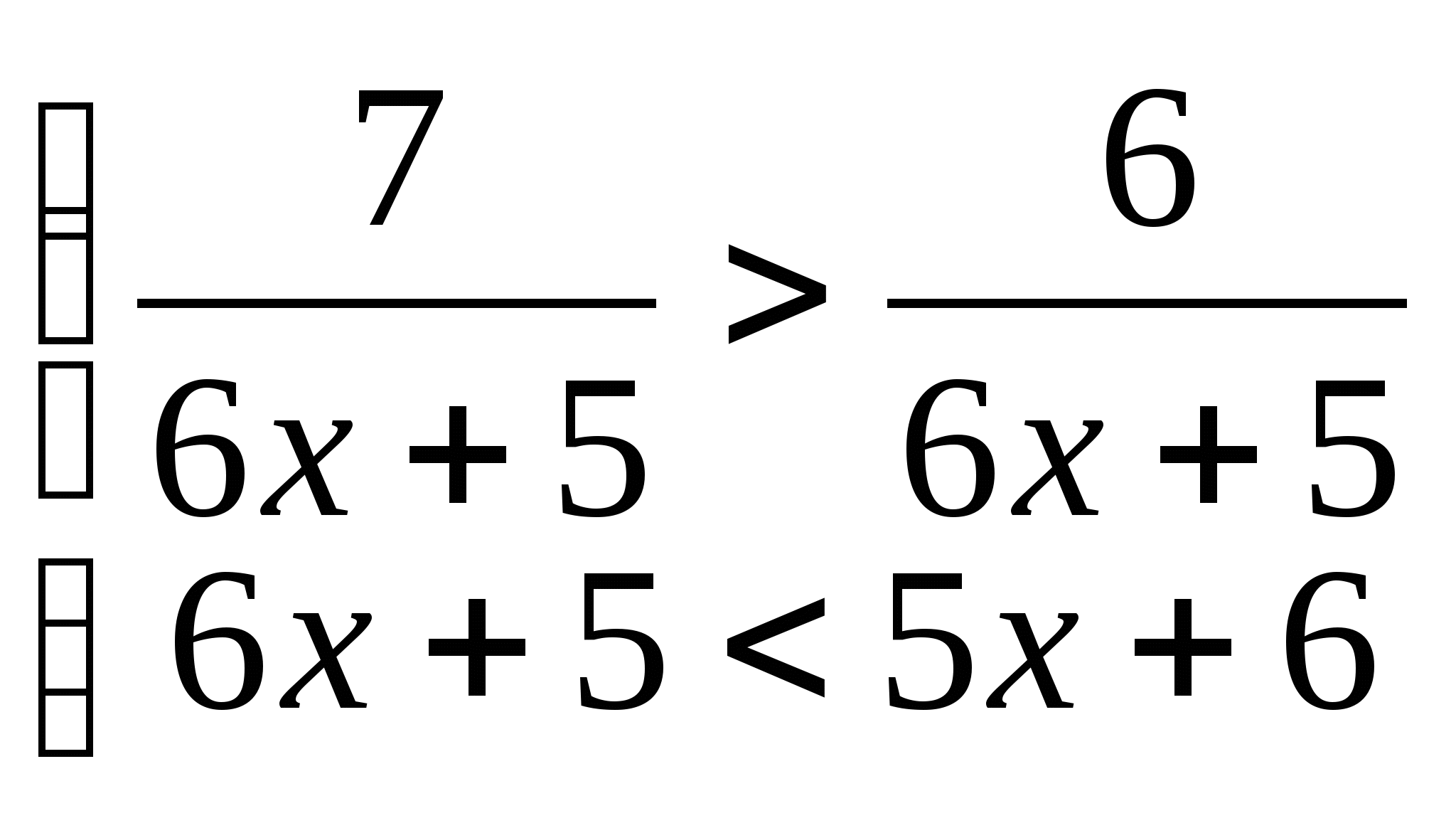
12. а) 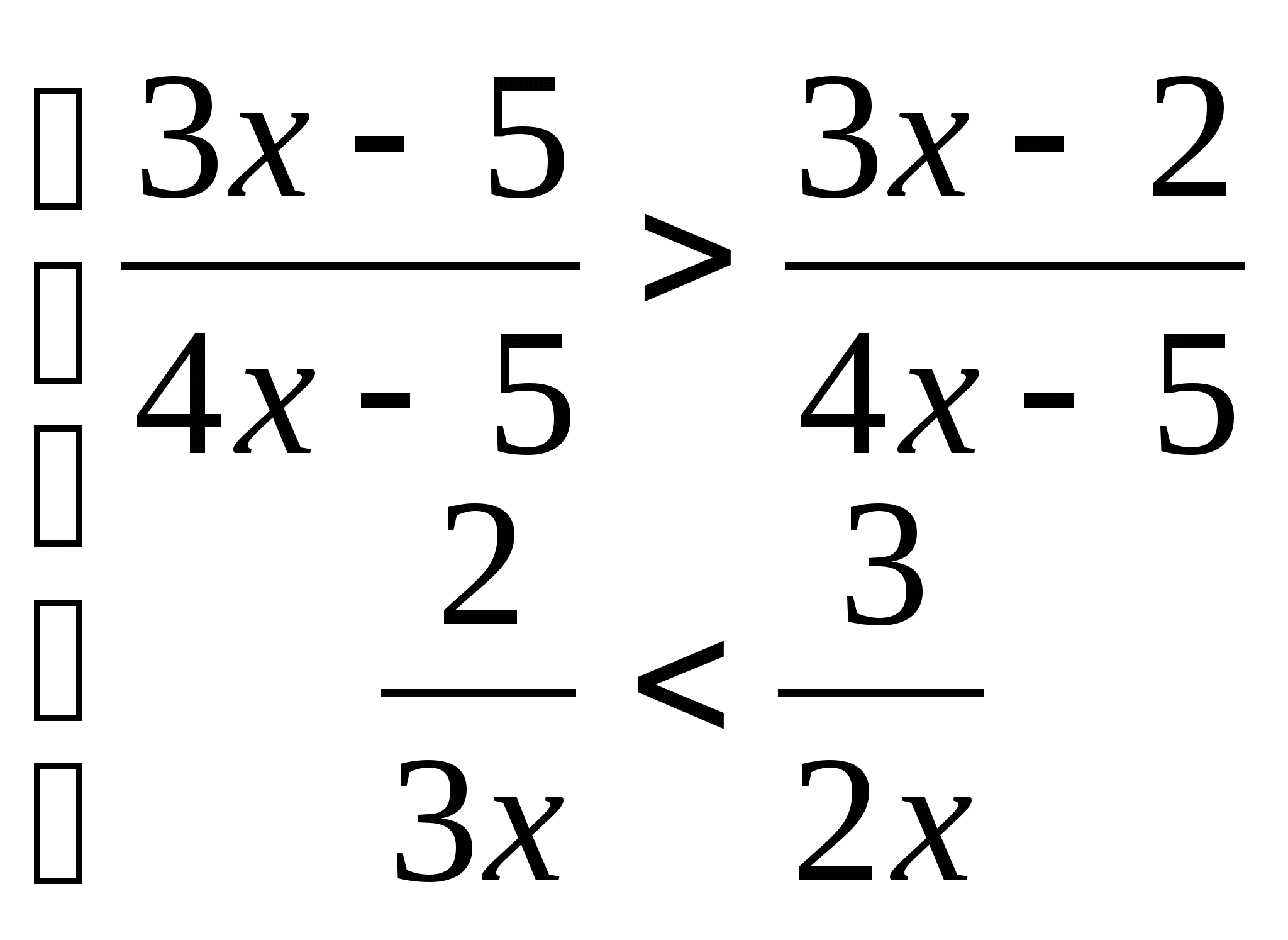 б)
б)
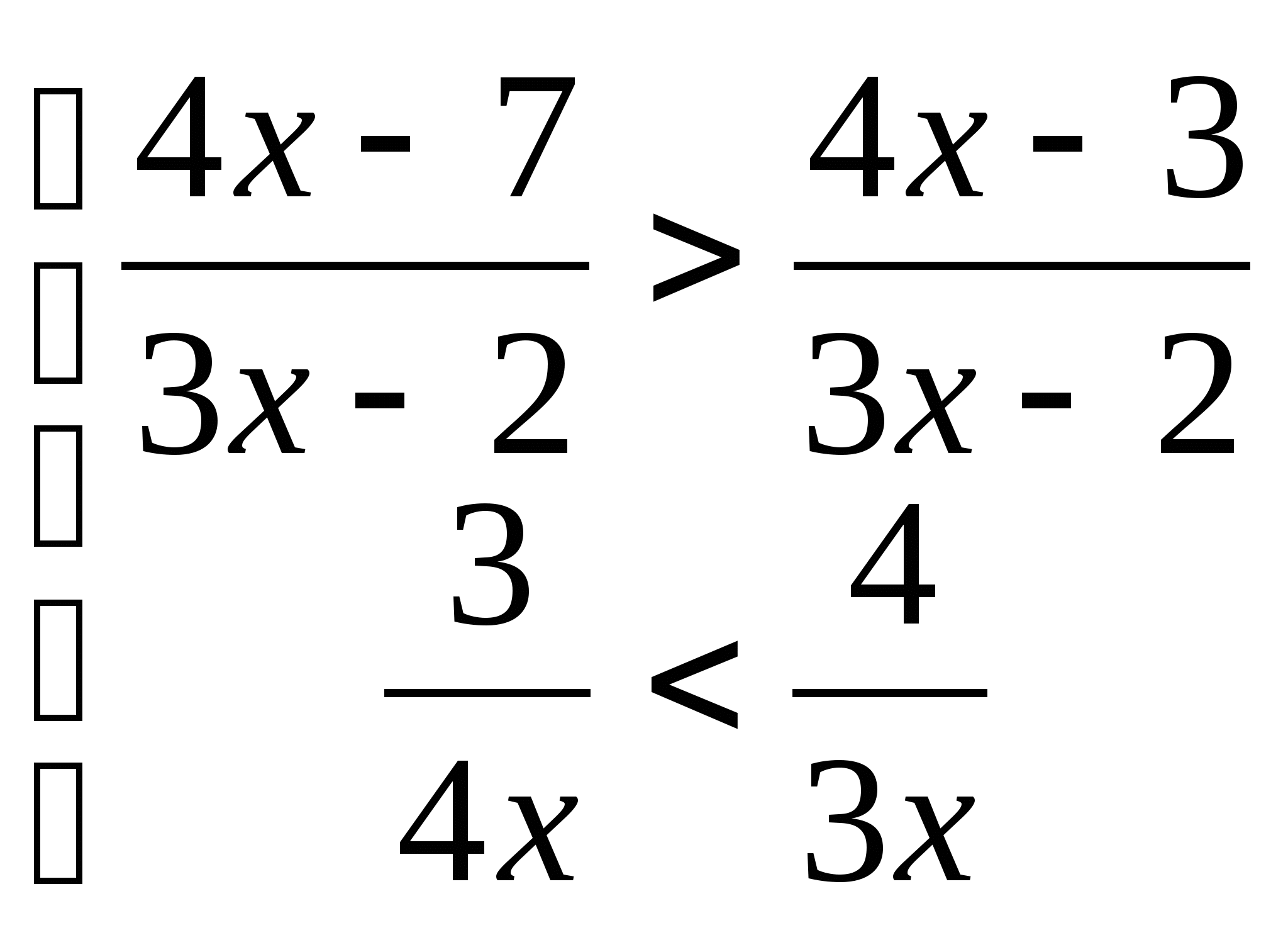
13. а) ![]() б)
б)
![]()
14. а) 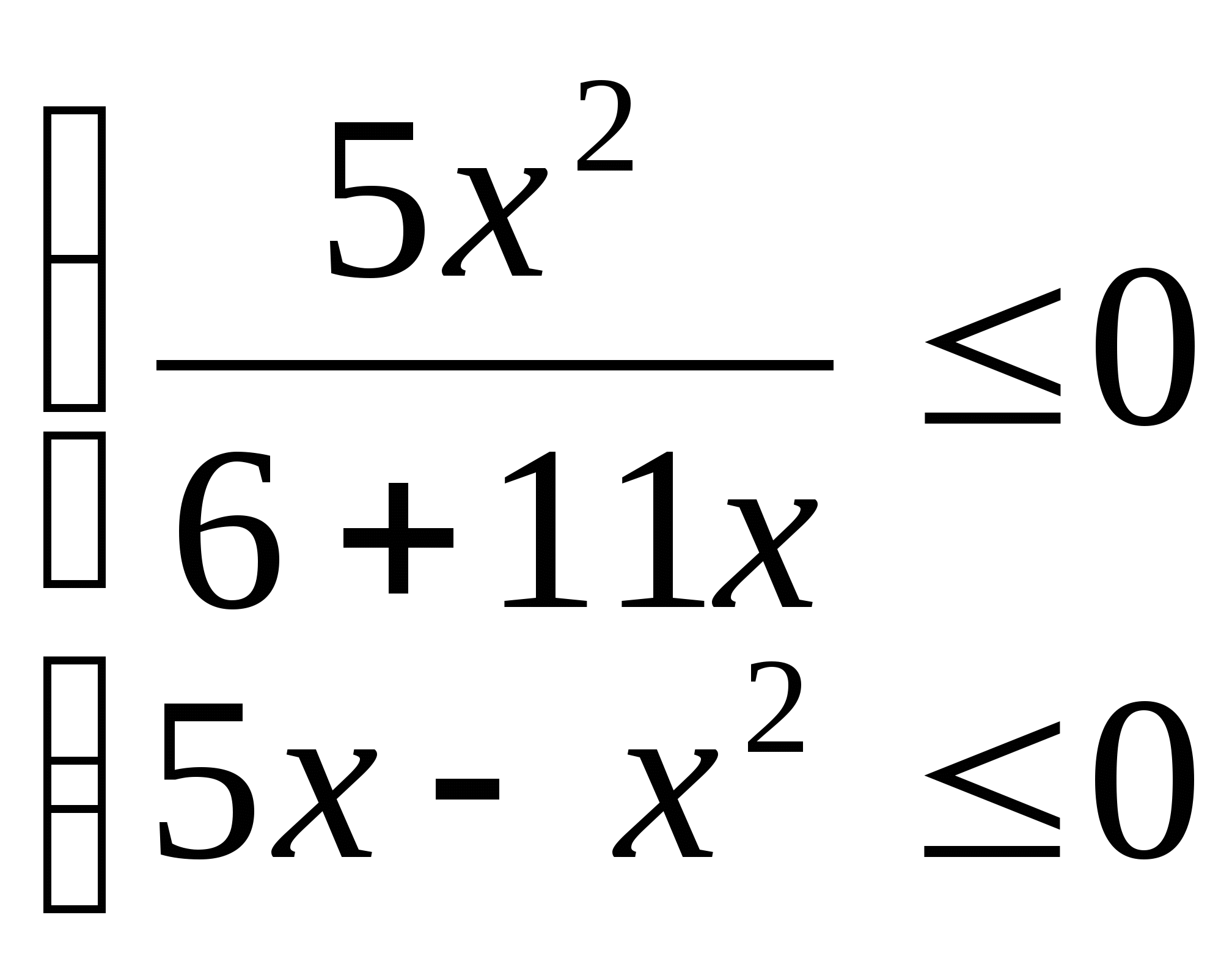 б)
б)
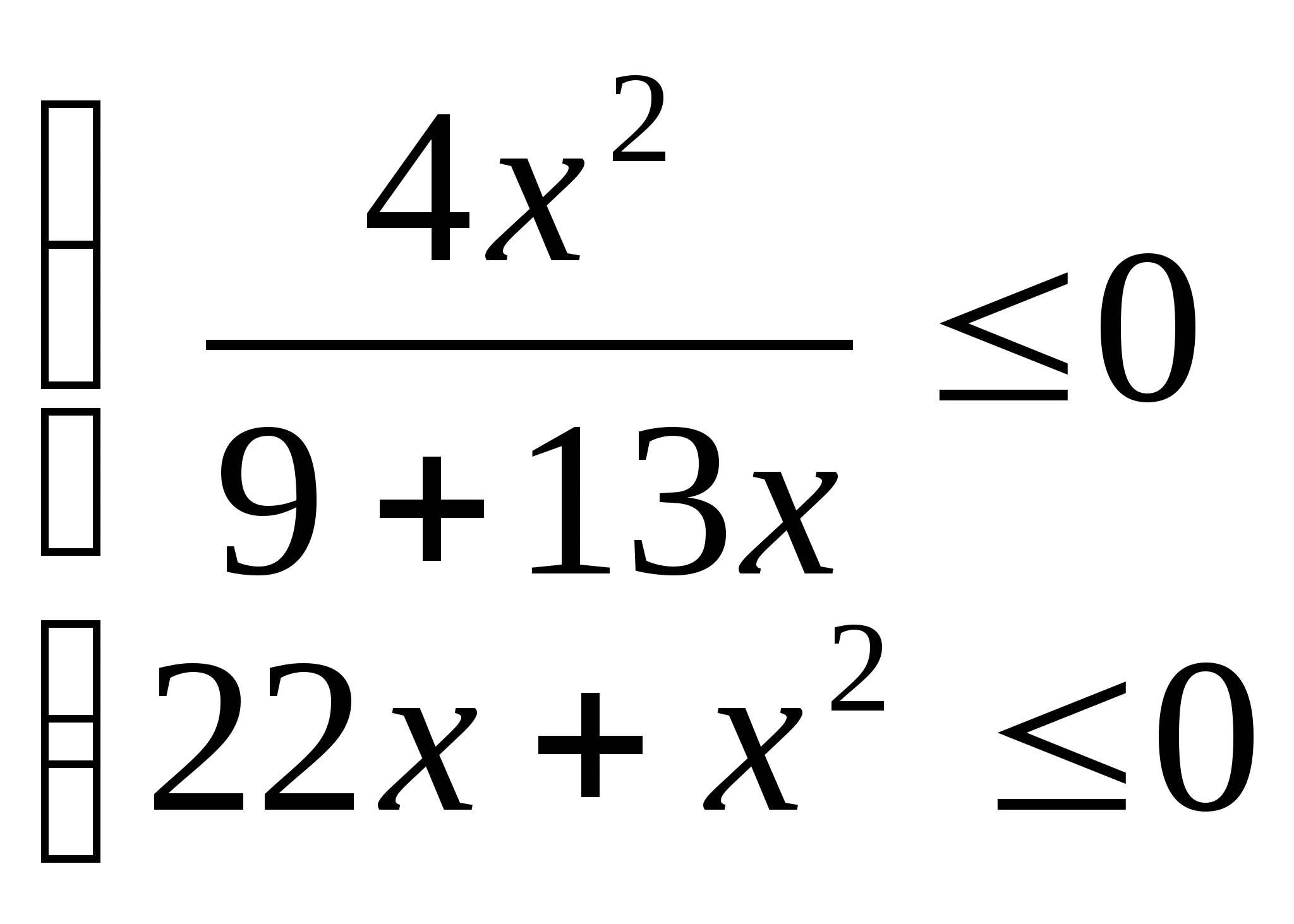
15. а) 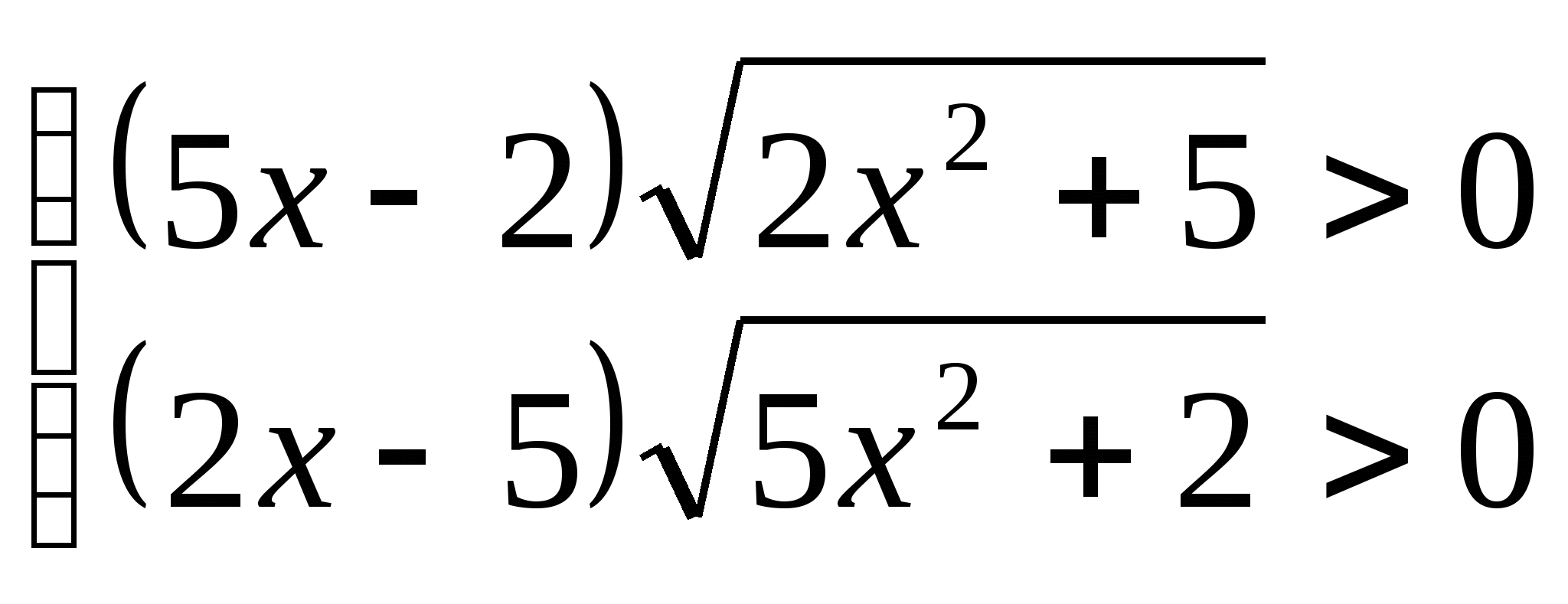 б)
б)
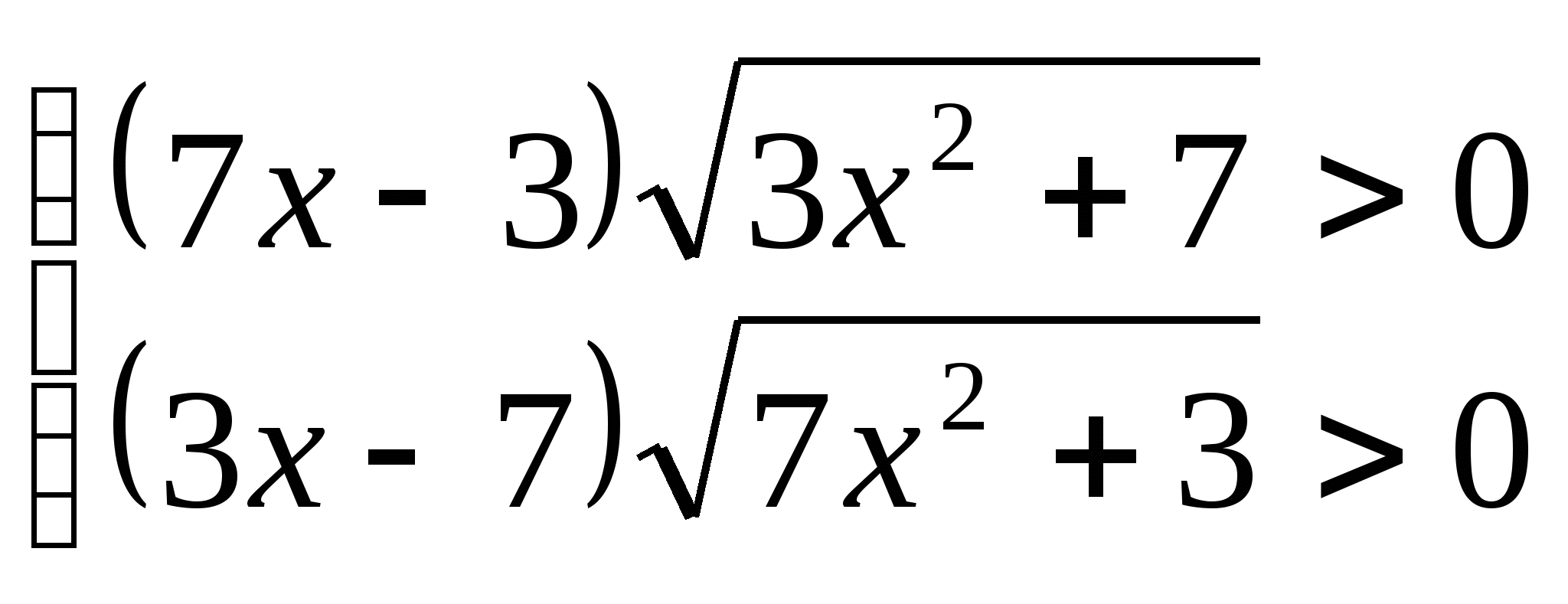
ФУНКЦИЯ
1.Построить график функции.
Используя график, найти:
1) область значения;
2) при каких значениях х функция принимает положительные значения.
а) ![]() б)
б)
![]()
2. а) ![]() б)
б)
![]()
3. а) ![]() б)
б)
![]()
4. а) ![]() б)
б)
![]()
5. а) ![]() б)
б)
![]()
6.Построить график функции
а) ![]() б)
б)
![]()
7. а) 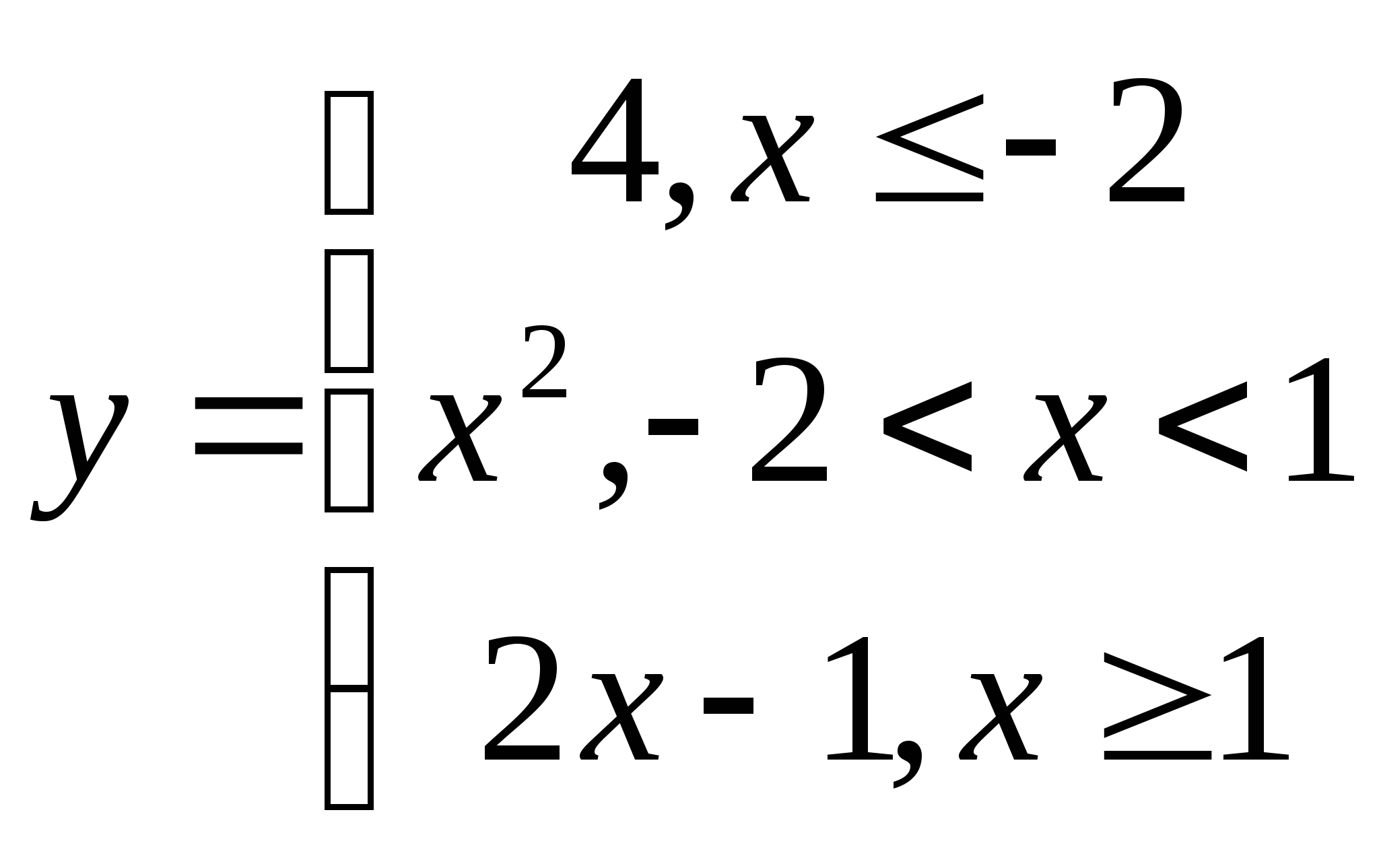 б)
б)
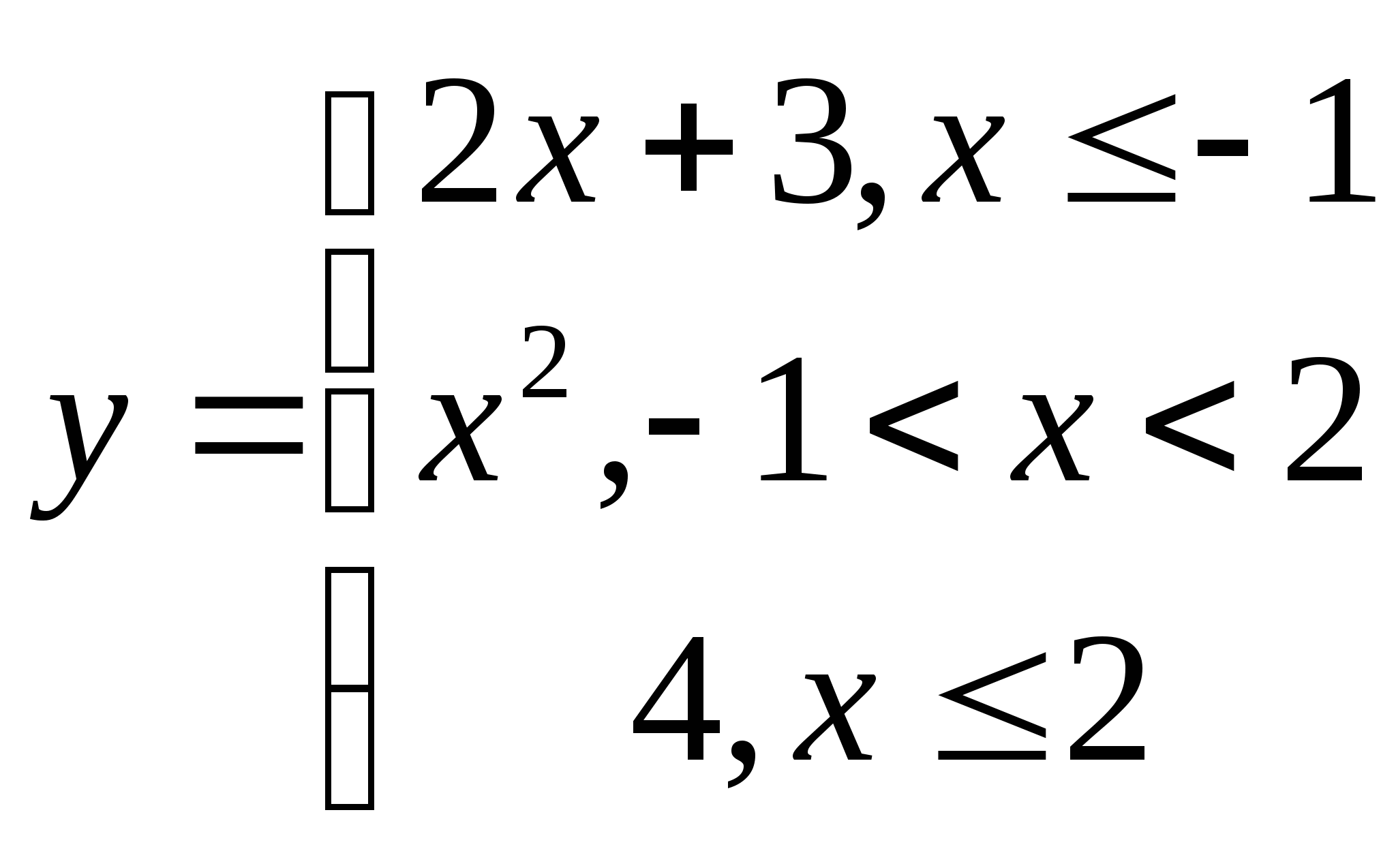
8. а) ![]() б)
б)
![]()
9. а) ![]() б)
б)
![]()
10. а) ![]() б)
б)
![]()
11.Найти область определения функции
а) ![]() б)
б)
![]()
12. а) ![]() б)
б)
![]()
13. а) ![]() б)
б)
![]()
14. а) ![]() б)
б)
![]()
15. а) ![]() б)
б)
![]()
ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА
Решить уравнение
1.а) ![]() б)
б)
![]()
2. а) ![]() б)
б)
![]()
3) ![]() б)
б)
![]()
4) ![]() б)
б)
![]()
5) ![]() б)
б)
![]()
6) а) ![]() б)
б)
![]()
7) а) ![]() б)
б)
![]()
8) а) ![]() б)
б)
![]()
9) а) ![]() б)
б)
![]()
Решить неравенство
1) а) ![]() б)
б)
![]()
2) а) ![]() б)
б)
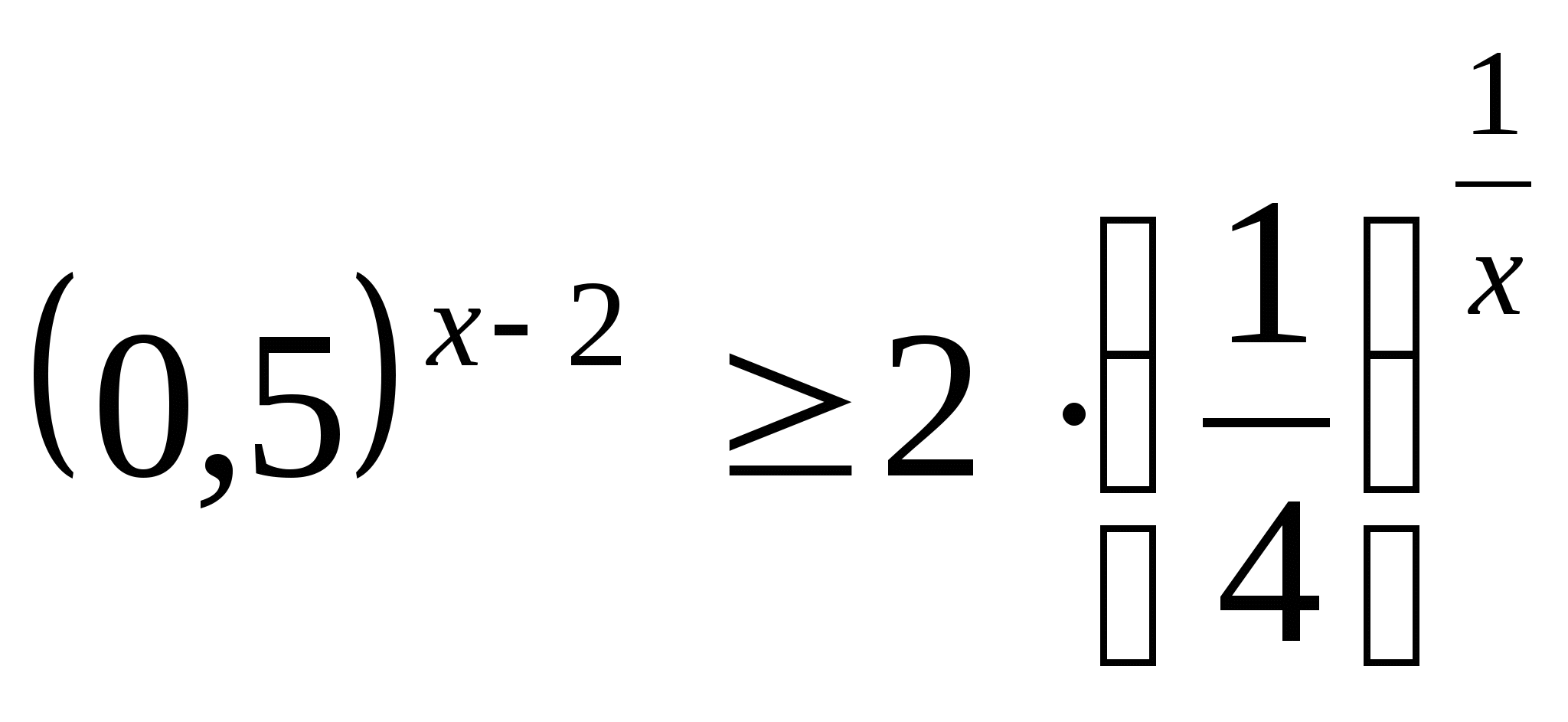
3) а) ![]() б)
б)
![]()
4) а) ![]() б)
б)
![]()
5) а) 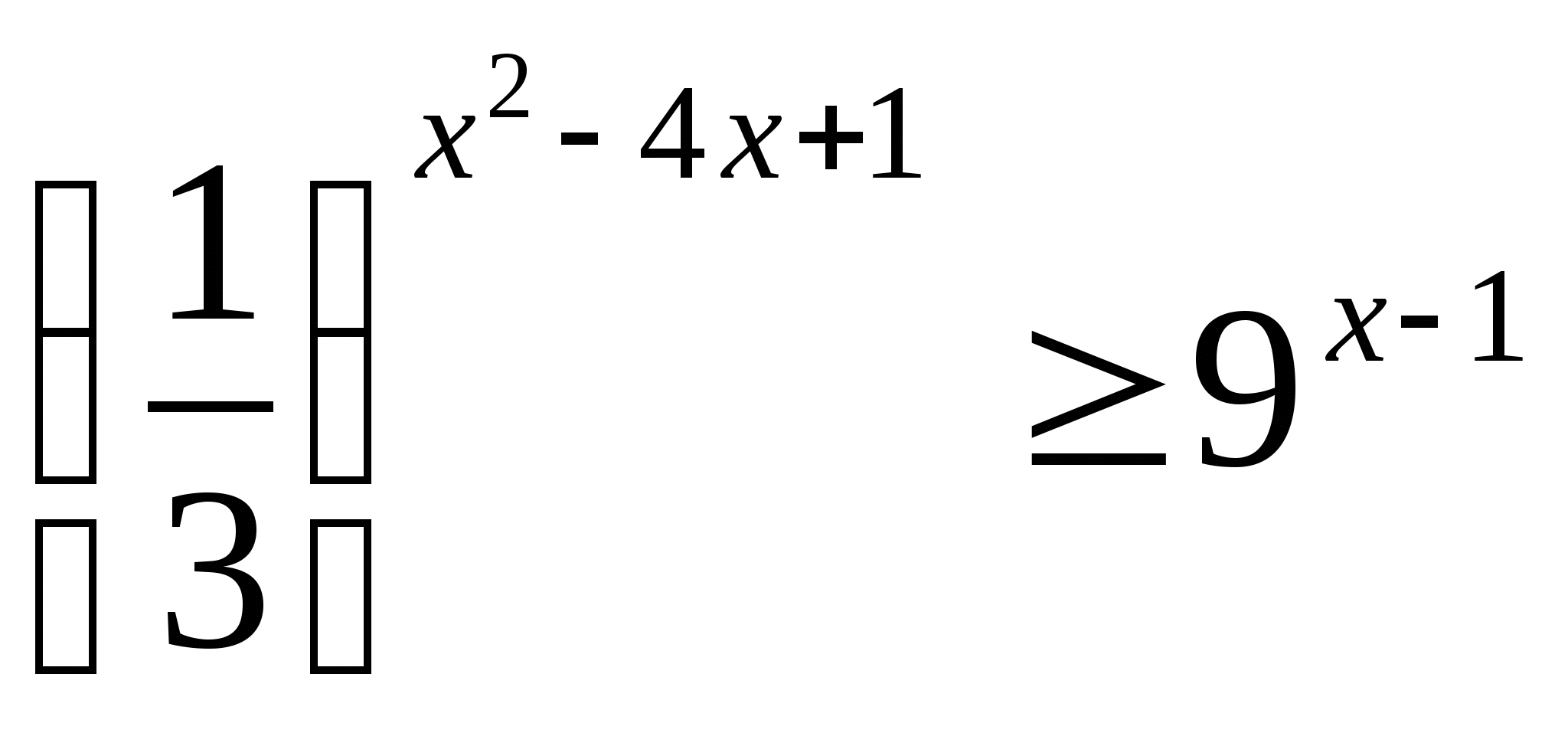 б)
б)
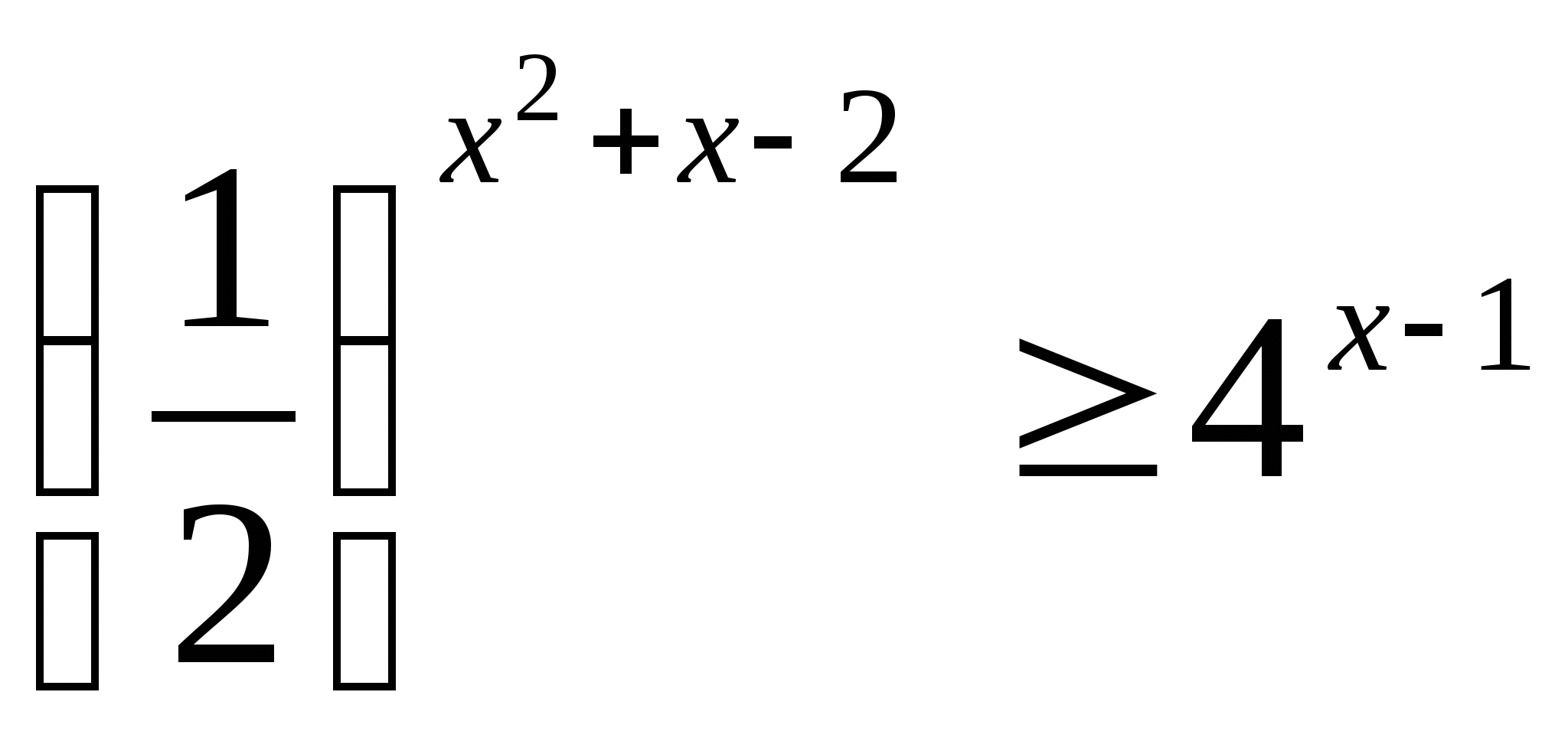
6) а) ![]() б)
б)
![]()
7) а) ![]() б)
б)
![]()
8) а) ![]() б)
б)
![]()
9) а) ![]() б)
б)
![]()
10) 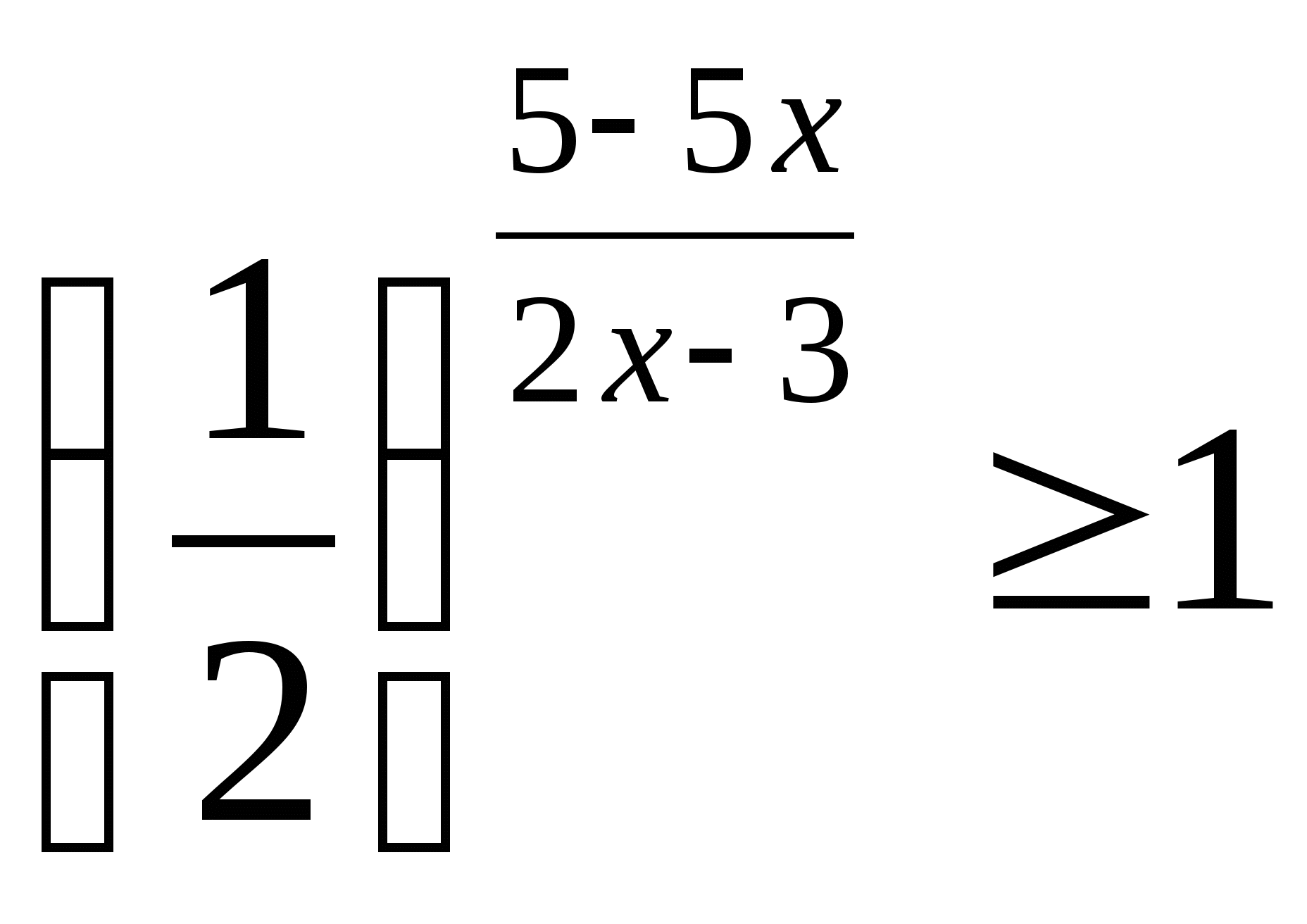 11)
11)
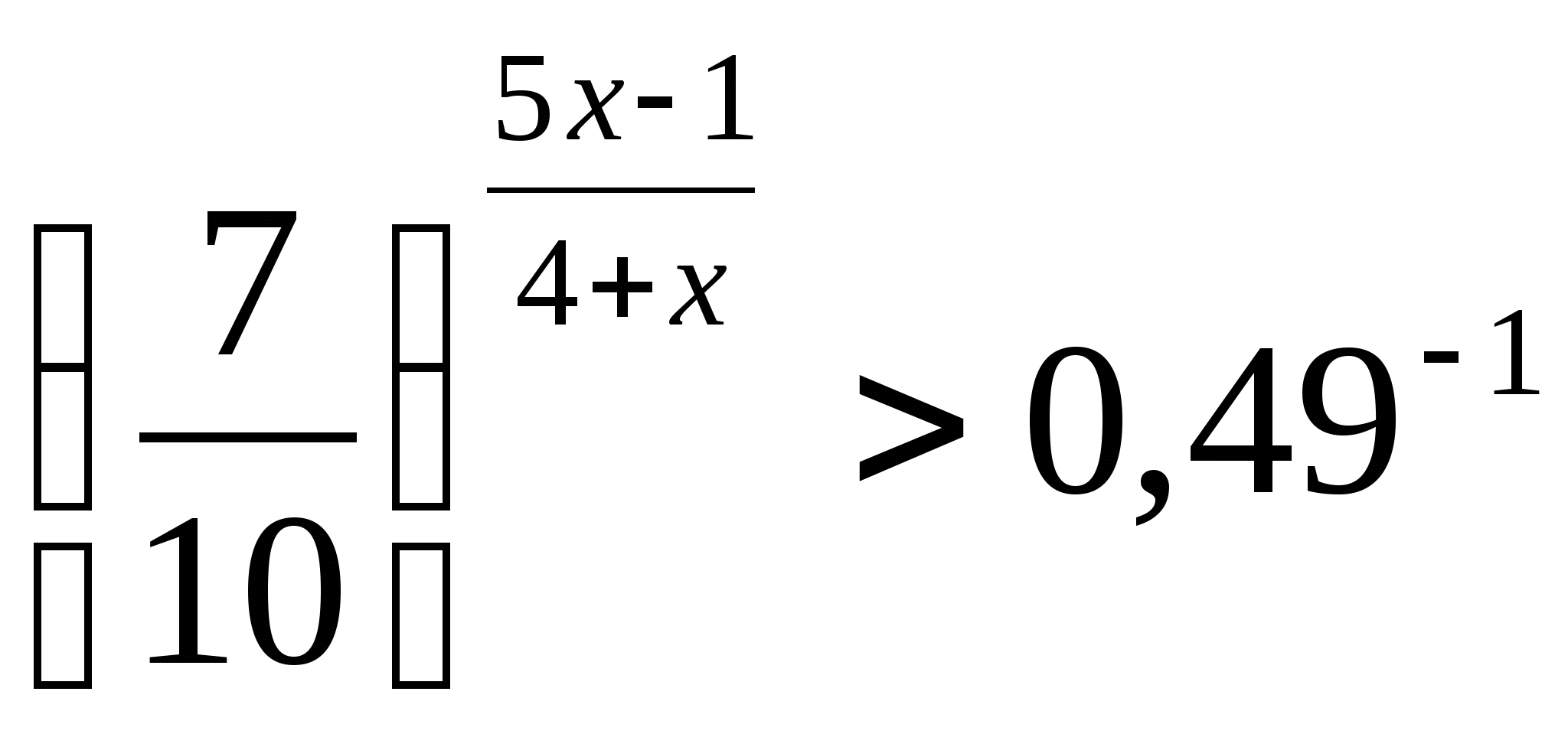 12)
12)
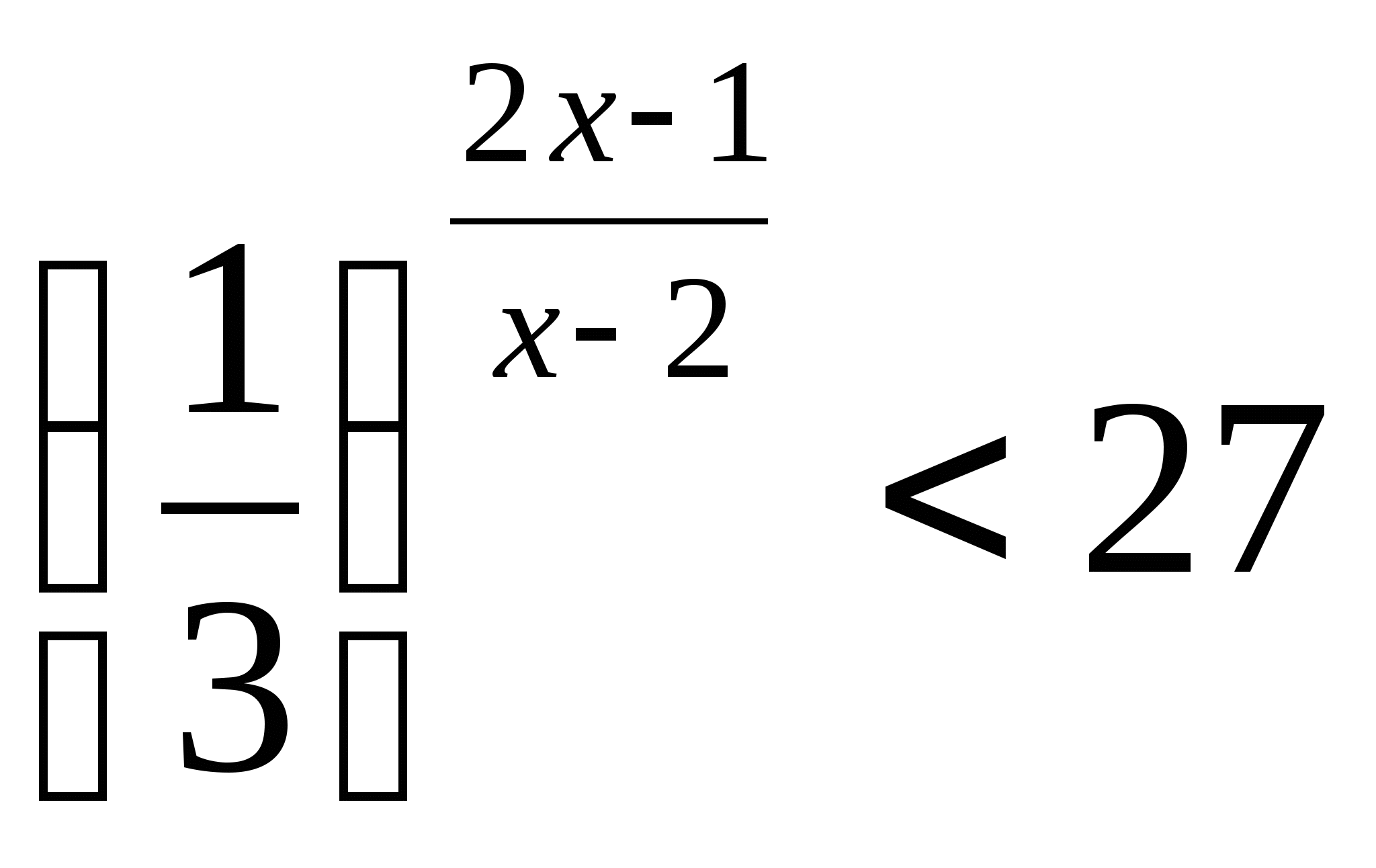 13)
13)
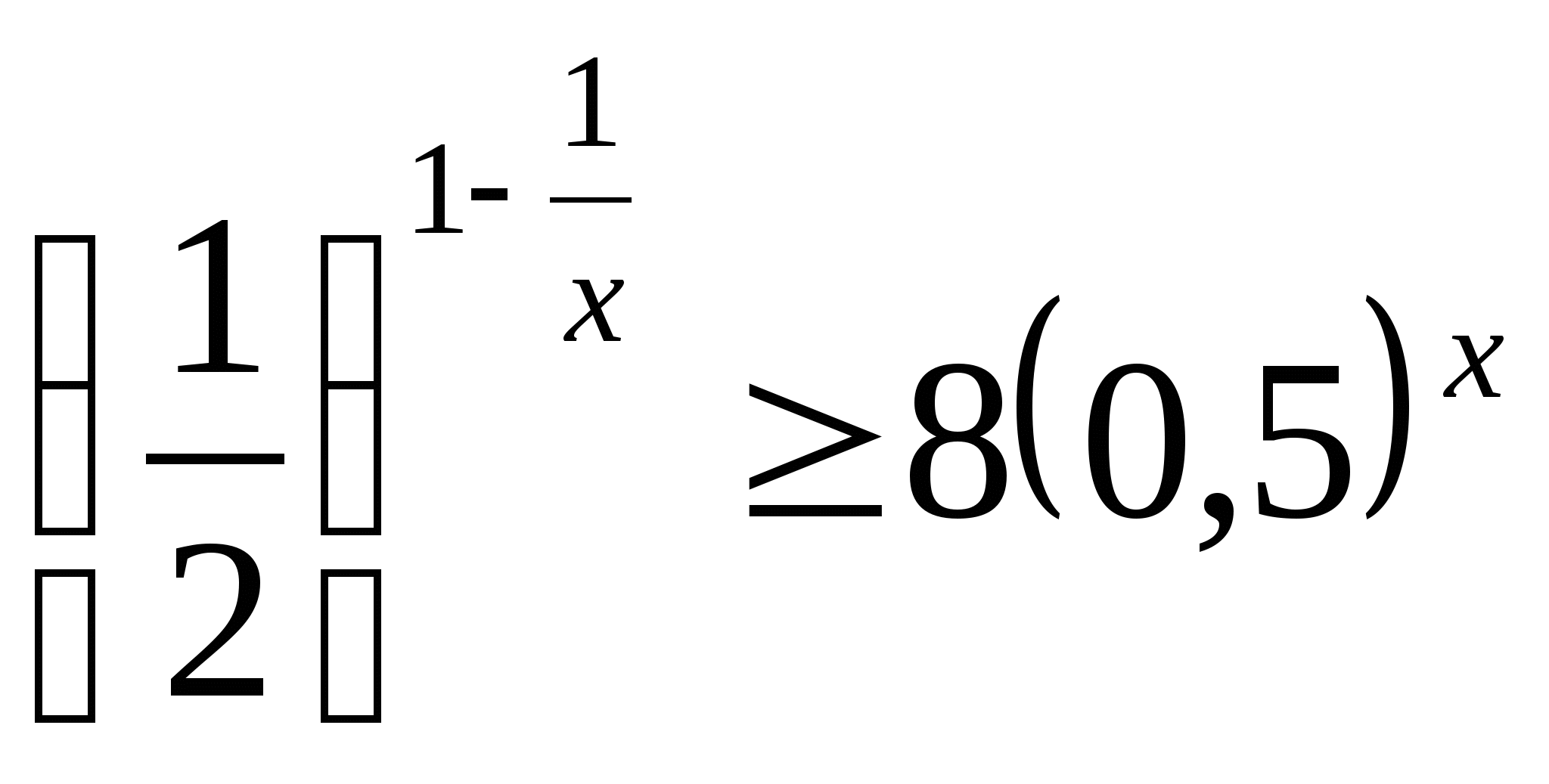
14) ![]() 15)
15)
![]() 16)
16)
![]()
17) ![]() 18)
18)
![]()
19) ![]() 20)
20)
![]()
ЛОГАРИФМЫ
1.Найти значение выражения
1.1. ![]() 1.2.
1.2. ![]() 1.3.
1.3. ![]() 1.4.
1.4. ![]()
1.5. ![]() 1.6.
1.6. ![]() 1.7.
1.7. ![]() 1.8.
1.8. ![]()
1.9. ![]() 1.10.
1.10. ![]() 1.11.
1.11. ![]()
1.12. ![]() 1.13.
1.13. ![]() 1.14.
1.14. ![]()
2. Решить уравнение
2.1. а) ![]() б)
б)
![]()
2.2. а) ![]() б)
б)
![]()
2.3. а) ![]() б)
б)
![]()
2.4. а) ![]() б)
б)
![]()
2.5. а) ![]() б)
б)
![]()
2.6. а) ![]() б)
б)
![]()
2.7. а) ![]() б)
б)
![]()
2.8. а) ![]() б)
б)
![]()
2.9. а) ![]() б)
б)
![]()
3.Решить неравенства
3.1. а) ![]() б)
б)
![]()
3.2. а) ![]() б)
б)
![]()
3.3. а) ![]() б)
б)
![]()
3.4.а) ![]() б)
б)
![]()
3.5. а) ![]() б)
б)
![]()
3.6. а) ![]() б)
б)
![]()
3.7. а) ![]() б)
б)
![]()
3.8. а) ![]() б)
б)
![]()
3.9. а) ![]() б)
б)
![]()
ТРИГОНОМЕТРИЯ
1.Упростить выражение
1.1.а) 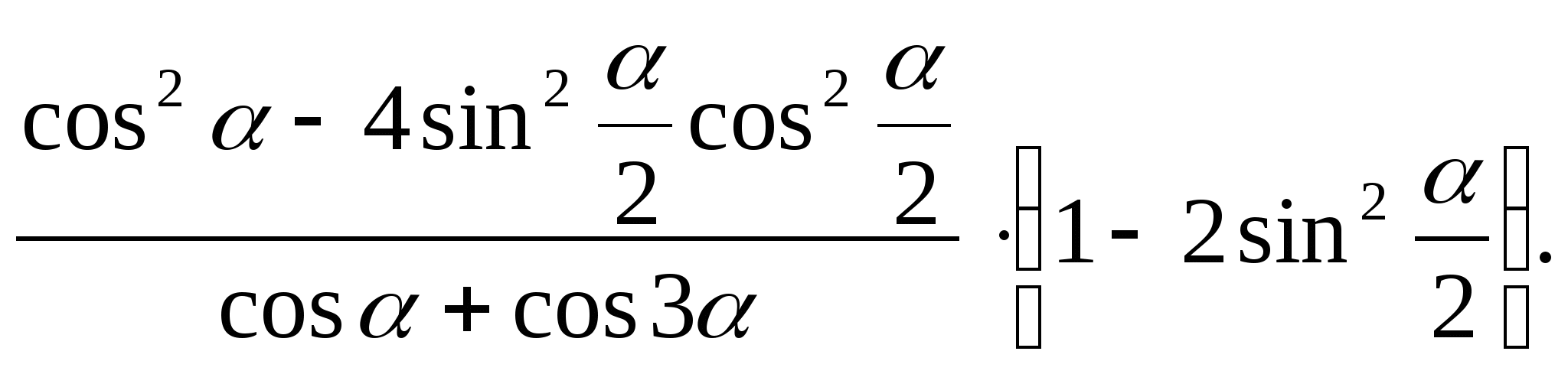 б)
б)
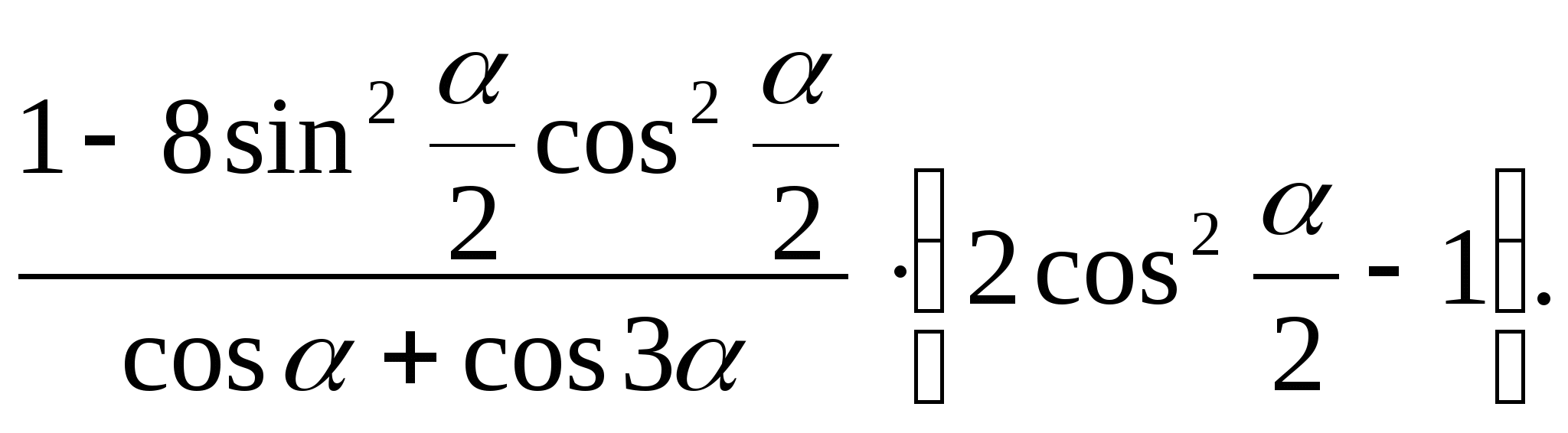
1.2.а) ![]() б)
б)
![]()
1.3.а) ![]() б)
б)
![]()
1.4. а) ![]() б)
б)
![]()
1.5. а) ![]() б)
б)
![]()
1.6. а) ![]() б)
б)
![]()
1.7. а) ![]() б)
б)
![]()
1.8. а) ![]() б)
б)
![]()
1.9. а) ![]() б)
б)
![]()
1.10. а) ![]() б)
б)
![]()
2.Найти численное значение выражения
2.1. а) ![]() б)
б)
![]()
2.2. а) ![]() б)
б)
![]()
2.3. а) ![]() б)
б)
![]()
2.4. а) ![]() б)
б)
![]()
2.5. а) ![]() б)
б)
![]()
2.6. а) ![]() б)
б)
![]()
3.Вычислить значение выражение при данном значении переменной
3.1. а) ![]() б)
б)
![]()
3.1. а) ![]() б)
б)
![]()
3.3. а) ![]() б)
б)
![]()
3.4. а) ![]() б)
б)
![]()
3.5. а) ![]() б)
б)
![]()
ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ
Уравнения, которые сводятся к квадратным
1.а) ![]() б)
б)
![]()
2.а) ![]() б)
б)
![]()
3.а) ![]() б)
б)
![]()
Однородные уравнения
1.а) ![]() б)
б)
![]()
2.а) ![]() б)
б)
![]()
Уравнения, которые решаются разложением на множители
1.а) ![]() б)
б)
![]()
2.а) ![]() б)
б)
![]()
3.а) ![]() б)
б)
![]()
4.а) ![]() б)
б)
![]()
5.а) ![]() б)
б)
![]()
6.а) ![]() б)
б)
![]()
Уравнения, которые решаются введением дополнительного угла
1.а) ![]() б)
б)
![]()
2.а) ![]() б)
б)
![]()
Уравнения, которые решаются при помощи формул понижения степени
1.а) ![]() б)
б)
![]()
2.а) ![]() б)
б)
![]()
Дробно-рациональные уравнения относительно тригонометрических функций
1.а) ![]() б)
б)
![]()
2.а) ![]() б)
б)
![]()
3.а) ![]() б)
б)
![]()
4.а) ![]() б)
б)
![]()
5.а) ![]() б)
б)
![]()
6.а) ![]() б)
б)
![]()
ПРОГРЕССИИ
(Смотри видеуроки 18, 20, 21, 23).
1. а) Первый член арифметической прогрессии
![]() , а
второй
, а
второй ![]() .
Найти седьмой член прогрессии.
.
Найти седьмой член прогрессии.
б) Первый член арифметической прогрессии ![]() , а
второй
, а
второй ![]() .
Найти пятый член прогрессии.
.
Найти пятый член прогрессии.
2. а) Первый член арифметической прогрессии
![]() ,
разность прогрессии
,
разность прогрессии ![]() .
Найти сумму десяти первых членов прогрессии.
.
Найти сумму десяти первых членов прогрессии.
б) Первый член арифметической прогрессии ![]() ,
разность прогрессии
,
разность прогрессии ![]() .
Найти сумму двенадцати первых членов прогрессии.
.
Найти сумму двенадцати первых членов прогрессии.
3. а) ![]() Сколько
положительных членов содержит арифметическая прогрессия 40; 37; 34;
…?
Сколько
положительных членов содержит арифметическая прогрессия 40; 37; 34;
…?
б) ![]() Сколько
положительных членов содержит арифметическая прогрессия 42; 38; 34;
…?
Сколько
положительных членов содержит арифметическая прогрессия 42; 38; 34;
…?
4. а) Найти сумму десяти первых членов
арифметической прогрессии ![]() если
если ![]()
б) Найти сумму десяти первых членов арифметической
прогрессии ![]() если
если ![]()
5. а) Первый член арифметической прогрессии равен -5, а разность равна 6. Сколько надо взять первых членов прогрессии, чтобы их сумма была равна 1040?
б) Первый член арифметической прогрессии равен 12, а разность равна -2. Сколько надо взять первых членов прогрессии, чтобы их сумма была равнялась -264?
6. а) Первый член геометрической прогрессии
![]() , а
знаменатель прогрессии
, а
знаменатель прогрессии ![]() Найти четвертый член прогрессии.
Найти четвертый член прогрессии.
б) Первый член геометрической прогрессии ![]() , а
знаменатель прогрессии
, а
знаменатель прогрессии ![]() Найти четвертый член прогрессии.
Найти четвертый член прогрессии.
7. а) Найти первый член и знаменатель
геометрической прогрессии ![]() ,
если
,
если ![]()
б) Найти первый член и знаменатель геометрической
прогрессии ![]() ,
если
,
если ![]()
8. а) Найти сумму бесконечной геометрической прогрессии 40; 20; 10;…
б) Найти сумму бесконечной геометрической прогрессии 81; 27; 9;…
9. а) Найти сумму пяти первых членов геометрической
прогрессии ![]() ,
если
,
если ![]()
б) Найти сумму шести первых членов геометрической
прогрессии ![]() ,
если
,
если ![]()
10. а) Сумма второго и третьего членов геометрической прогрессии равна 30, а разность четвертого и второго - 90. Найти пятый член .
б) Разность четвертого и второго членов геометрической прогрессии равна 30, а разность четвертого и третьего - 24. Найти пятый член .
8.ВОПРОСЫ К ЭКЗАМЕНУ
1. Натуральные числа. Действия с натуральными числами. Метод математической индукции
2. Целые числа, правила сложения, умножения и деления с целыми числами
3. Дробные числа. Обыкновенные и десятичные дроби. Действия над ними
4. Квадратные корни. Свойства квадратного корня
5. Действительные числа. Десятичная запись действительного числа. Действия на множестве действительных чисел
6. Числовая прямая. Модуль числа
7. Проценты. Задачи на проценты
8. Пропорция, основное свойство пропорции
9. Функция, определение и способы задания
10. Свойства элементарных функций
11. Графики элементарных функций
12. Предел функции
13. Производная функции, таблица производных
14. Первообразная для функции
15. Определённый интеграл
16. Таблица интегралов. Формула Ньютона-Лейбница
17. Комбинаторика. Перестановки, сочетания и размещения
18. Бином Ньютона
19. Вариационный ряд. Размах, мода и медиана ряда
20. Статистическое распределение. Полигон
21. Среднее ряда
22. Дисперсия и среднее квадратичное отклонение
Примерный вариант контрольной работы
1. Найти значение выражения ![]()
2. Вкладчик положил в банк 40 000 грн. под 8% простых годовых. Сколько денег будет на его счёте через 3 года?
3. Построить график ![]()
4. Используя правила и формулы дифференцирования
найти производные функций: 1)![]()
2) ![]() 3)
3)
![]() 4)
4)
![]()
5. Вычислить интеграл 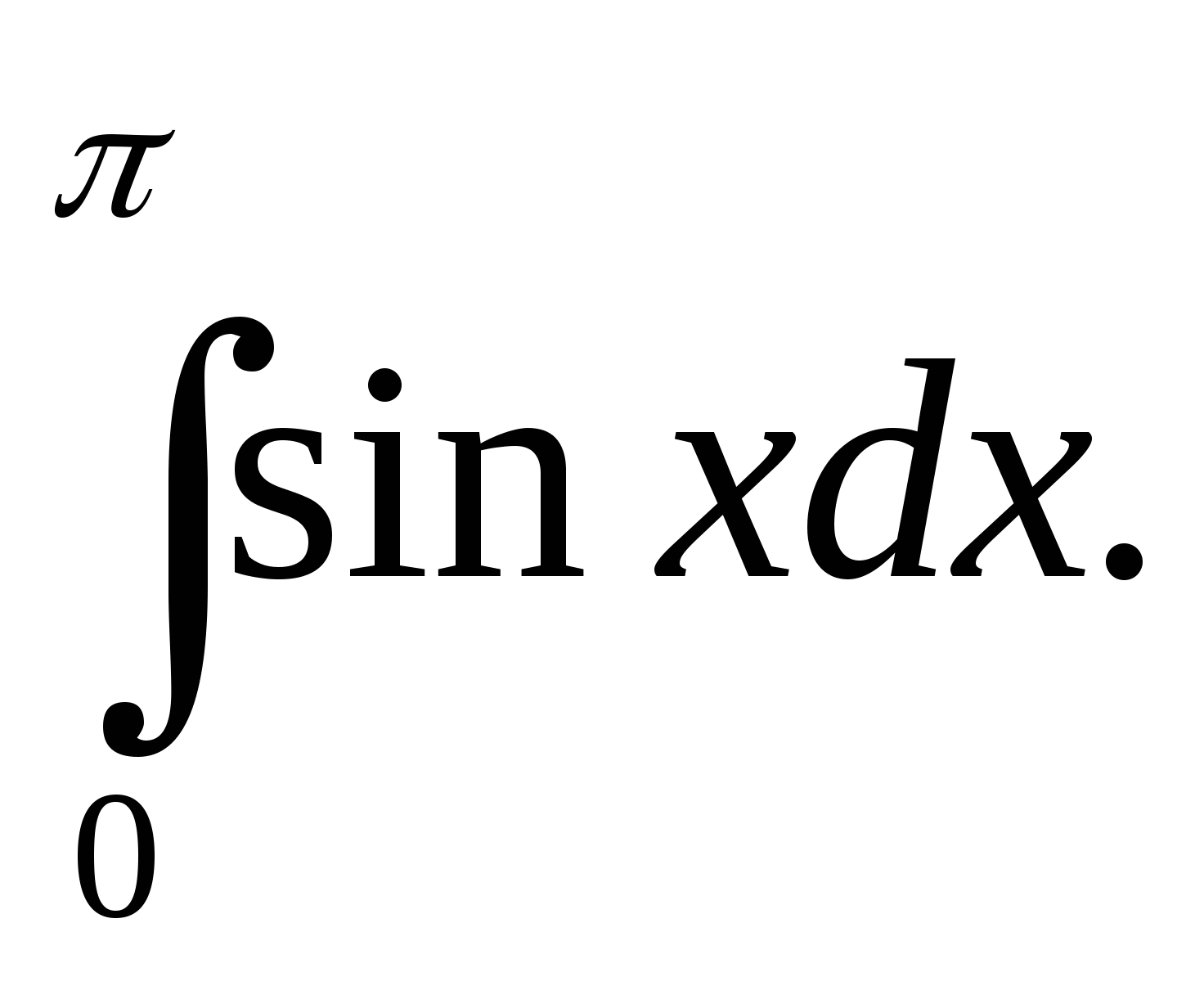
6. Найти разложение: ![]()
7. Сколько трехзначных чисел можно составить из цифр 1,2,3,4, если цифры не повторяются?
8. Группа студентов из 12 человек сдают экзамен по математике. Знания оценивались по пятибалльной системе. Оценки, полученные студентами соответствующие списку, такие: 5,4,4,3,4,2,2,5,5,3,3,4. Найти медиану этого распределения.
ЛИТЕРАТУРА
1. Азаров А.И. Функциональный и графический методы решения экзаменационных задач / Азаров А.И., Барвенов С.А.--- Мн.: Аверсэв, 2004. - 222 с.
2. Бардушкин В. Тригонометрические уравнения. Отбор корней / В. Бардушкин, А. Прокофьев.// Математика, №12, 2005. - 23-27 С.
3. Бородин П. Тригонометрия. Материалы вступительных экзаменов в МГУ[текст] / П. Бородин, В. Галкин, В.Панфёров, И. Сергеев, В. Тарасов//Математика №1, 2005. 36-48 С.
4. Василевский А.Б., Задания для внеклассной работы по математике / А.Б. Василевский --- Мн.: Народная асвета. 1988. -- 176 с.
5. Выгодский Я.Я., Справочник по элементарной математике. / Выгодский Я.Я. --- М.: Наука, 1970. -231 с.
6. Гальперіна А.Р. Математика. ЗНО 2009 / С.М. Будна, О.С. Будна, А.Р. Гальперіна, М.Я. Забєлишенська, О.Я. Михеєва - К: Літера, 2009. -320 с.
7. Гальперіна А.Р. Математика. ЗНО 2011 / А.Р. Гальперіна, О.Я. Михеєва - К: Літера ЛТД, 2011, - 120 с. + Додат.(16 с.).
8. Игудисман О. Математика на устном экзамене/ Игудисман О. --- М.: Айрис пресс, Рольф, 2001. -215 с.
9. Сапунов П.И. Преобразование и объединение групп общих решений тригонометрических уравнений / Сапунов П. И. // Математическое просвещение, выпуск №3, 1935. -320 с.
10. Семенець В.В. Математика для вступників до ВУЗів / М.Ф. Бондаренко, В.А. Дікарєв, О.Ф. Мельников, Семенець В.В., Шкляров Л.Й. // Навчальний посібник, Харків, Компанія СМІТ, 2002. -225 с.
11. Сканави М.И. Сборник задач по математике для поступающих во ВТУЗы / В.К. Егерев, В.В. Зайцев, Б.А. Кордемский и др.; Под ред М.И. Сканави - М: ОНИКС, Мир и Образование, 2006. -523 с.
12. Шарыгин И.Ф. Факультативный курс по математике: решение задач / Шарыгин И.Ф., Голубев В.И. --- М.: Просвещение, 1991. -1-3 с.
13. Шевкин А.В. ЕГЭ. Математика. Задания С6 / А.В.Шевкин, Ю.О. Пукас. - М.: Экзамен, 2012.
14. Шевкин А.В. Текстовые задачи по математике. 7-11 кл. - М.: Илекса. 2012.
56