Разработка урока на тему: Аналогия в геометрии (мастерская) 9 класс

КГУ «Средняя общеобразовательная школа- лицей №7»

Разработка урока на тему:

Аналогия в геометрии

(мастерская)

Класс 9 «Б»

Дата проведения:

Учитель математики: Шукыжанова А.С

Г.Семей

2015

Тема урока: Аналогия в геометрии

Аннотация

Один из путей познания, который прослеживается в мастерской, состоит из таких этапов: мысль, цепочка размышлений и, наконец, строго логически обоснованный, желанный результат поиска. При использовании этого пути мысль не тормозит фантазии, не закрывает интуитивного поиска, нет погони за мыслями, нет быстрого скачка к цели, зато царствует спокойное, неторопливое восприятие, наблюдение, появляется чувствительность, которая обогащает поиск, приводит к цели.

В каждой мастерской ученик - творец, он получает право на свободный поиск, право на самооценку: самое ответственное, самое серьезное, самое трудное право.

Он получает право распоряжаться своим временем, у него исчезает страх перед выбором, хотя не исчезает ответственность за выбор, которая теперь возложена на него, но не снята с учителя.

Надо заметить, что общение с учеником-творцом открывает и новые перспективы для совершенствования самого учителя, ибо, как и для учеников, так и для учителя нет предела совершенства.

Цель: обобщение и систематизация знаний и умений учащихся по теме.

Задачи:

а) развитие познавательной активности на основе поисковой деятельности;

б) развитие мыслительной деятельности;

в) воспитывать волю и настойчивость для достижения конечных результатов.

Технология: мастерская.

Метод обучения: проблемно - поисковый.

Ход урока:

1. Организационный момент

1. Проверка домашнего задания

2. Фронтальный опрос:

а) Какой угол называется трехгранным?

б) Как можно построить трехгранный угол?

в) Элементы трехгранного угла и их обозначения.

г) Как можно определить двугранный угол трехгранного угла при

каждом ребре?

Вступление учителя

Ребята, сегодня мы рассмотрим аналоги некоторых теорем планиметрии в пространстве. Для решения данной задачи поэтапно выясним ответы на следующие вопросы:

1. Зависит ли величина плоского угла от расположения вершины двугранного угла?

2. По данному расстоянию t от вершины трехгранного угла до вершины двугранного угла можно ли выразить плоский угол через t?

3. Как можно доказать теорему косинусов с помощью векторов?

Будете работать по 5 группам.

Исследуйте проблему (I) парами

Задания для групп

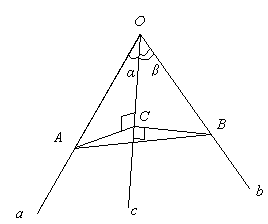
а)

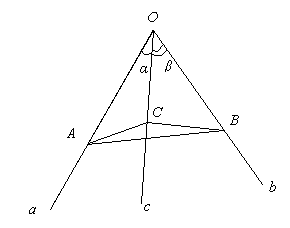
Постройте двугранный угол при ребре с, с вершиной С где

ОС= 4 см,

α = 30^о,

β = 45^о.

Найти: γ.

б)

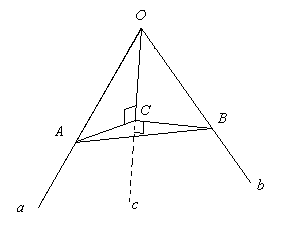
Дано: Оabc - трехгранный угол, двугранный угол при вершине С находится от О на расстоянии 5 см.

ОС= 4 см,

α = 30^о,

β = 45^о.

Найти: γ.

Решение:

а) АС_┴с, ВС_┴с;

из ∆АВО, где ОСА=90^о

АС = ОСtgβ=4tg45^o=4 (см)

AO= (см)

Их ∆ВСО, где ОСВ=90^о

ВС=ОСtgα=4tg30^o=(см)

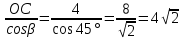OB= (см)

из ∆АCB, где С=60^о

Из ∆АВО, где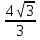=γ

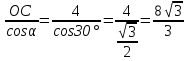
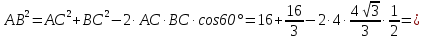
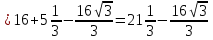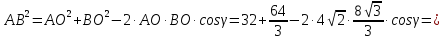б) АС=5см, см, ОВсм, АО см

=

=

=

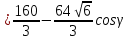
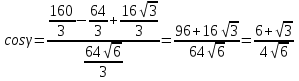
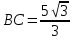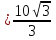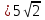
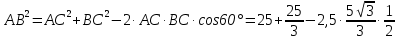
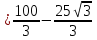
Слушаем ответы пар

Если величина плоского угла не зависит от расположения точки С, то она зависит от величины углов α, β, с.

Посмотрите на свой рисунок трехгранного угла, сосредоточье своё внимание лишь на углу и попробуйте найти его с помощью данных величин.

Работают в группах

Задания для исследования:

1. Найти угол γ, по данным α, β, с по теореме косинусов, если

2. Найти угол γ, по данным α, β, с по теореме косинусов, если

3. Найти угол γ, по данным α, β, с по теореме косинусов, если

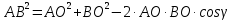
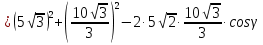
4. Найти угол γ, по данным α, β, с =.

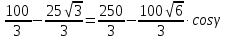Слушаем групп

1)

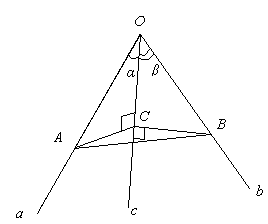
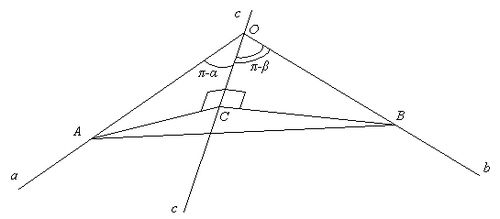
Дано: Oabc - трехгранный угол

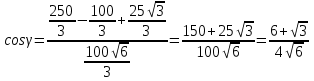
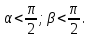
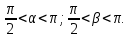АС_┴с, ВС_┴с;

Найти:

Решение:

Из ∆АCB, по теореме косинусов

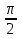
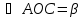
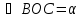
из ∆АОВ, по теореме косинусов

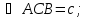
Сравнивая 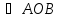, имеем

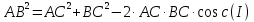
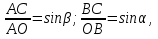
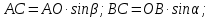
2) Если α и β - тупые углы, то рассмотрим луч с, дополняющий с до прямой, и имеем трехгранный угол Oabc, в нем два острых угла (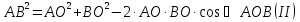),(),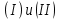 третий - искомый угол.

Решение:

=

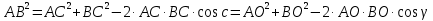
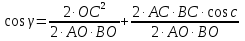
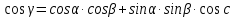
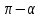
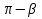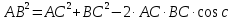
3)

Решение:

a)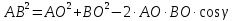

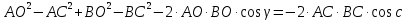
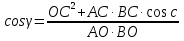
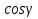
б) Из ∆АCB

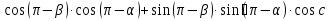
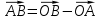
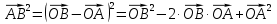
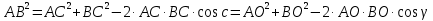
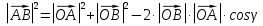
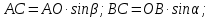
4) Если двугранный угол при ребре с прямой, то стороны выражаются с помощью теоремы Пифагора. Аналогом полученного равенства является теоремы Пифагора для «прямоугольного» трехгранного угла: его «гипотенуза» γ выражается через «катеты» α и β.

Сегодня на уроке нам пришлось проделать большой путь, чтобы убедиться в том, что для формул, изученных в планиметрии существуют аналоги в пространстве.

Первичное осмысление полученных результатов.

Известны три плоских угла трехгранного угла.

Как вы будете их искать:

а) угол между его ребром и плоскостью противолежащей грани.

б) расстояние от некоторой точки ребра до плоскости противолежащей грани.

Дано: Oabc - трехгранный угол

AD 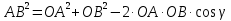(BOC)

AC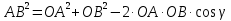 c, тогда CD 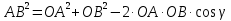c

= γ

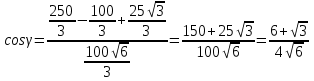
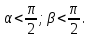
Найти: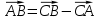

Решение: 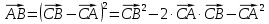- линейный угол при ребре с.

Пусть АО=x , тогда

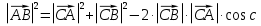
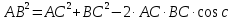
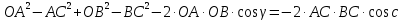
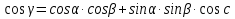
, из ∆АОВ, где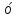

;

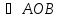
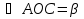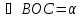
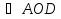
Домашнее задание:

Исследуйте формулы теоремы синусов, т.е. найдите аналогию теоремы синусов в пространстве.