- Учителю
- Занятие-практикум по математике «Квадратные уравнение»- 9 класс
Занятие-практикум по математике «Квадратные уравнение»- 9 класс
Занятие-практикум по математике
-
Тема модуля «Квадратные уравнение»
-
Класс: 9 «В»
-
Учитель: Сон Светлана Вильевна
-
Обоснование: Квадратные уравнения в школьном курсе алгебры занимают ведущее место. На их изучение отводится времени больше, чем на любую другую тему школьного курса математики. Сила теории уравнений в том, что она не только имеет теоретическое значение для познания естественных законов, но и служит конкретным практическим целям. Квадратные уравнения широко используется в таких темах, как «Квадратичный трехчлен», «Квадратичная функция», большинство задач о пространственных формах и количественных отношениях реального мира сводится к решению квадратных уравнений. Овладевая способами их решения, люди находят ответы на различные вопросы из науки и техники (транспорт, сельское хозяйство, промышленность, связь и т.д.). Так же для формирования умения решать уравнения большое значение имеет самостоятельная работа учащегося при обучении решения уравнений. Многие виды уравнений, предлагаемых в курсе 10-11 классов, решаются при помощи квадратных уравнений. Данная тема используется как на ВОУД, так и на ЕНТ.
-
Цель данного урока -практикума - показать, что изучение «Квадратных уравнений» могут быть использованы как эффективное средство закрепления, углубления, повторения и расширения теоретических знаний, для развития творческой математической деятельности на уроках математики для учащихся ресурсного центра.
-
Занятие включало триединую задачу обучающего, развивающего и воспитательного характера и было направлено на смягчение зон затруднений и ликвидацию пробелов основных моментов темы учащихся ресурсного центра.
-
Ожидаемый результат: повышение уровня обученности учащихся МКШ на 10%; выполнение на 85% работы, направленной на совершенствование способов учебно-познавательной деятельности; решение коммукативных задач;
Формы и методы организации урока:
-
работа в малых группах
-
мозговой штурм
-
снежный ком
Технология:
-
обучение в сотрудничестве.
1.Проверка знаний и умений учащихся. Урок начался с повторения ранее изученного материала, необходимый для выполнения самостоятельной работы. «Мозговой штурм»
а) что такое уравнение?
б) что называют корнем уравнения?
в) что значит решить уравнения?
г) какие виды уравнения вы знаете?
д) какие способы решения уравнений вы знаете?
Дети были активны, практически все знали ответы на задаваемые вопросы, отвечали правильно без затруднений и подсказок. Выполняя задания по ранее изученному материалу, было видно, что ученики поняли тему. Задания выполняли быстро без ошибок, объясняя каждый момент решения. Ребята выполнили «Входное тестирование». Данная работа не вызвала трудностей.
Качество 51,2%, Успеваемость - 88,9%


2. Изучение нового материала. Эта работа вышла за рамки школьного учебника, но способы «переброски коэффициентов» и «сложения коэффициентов» позволяют ученикам легко и быстро находить корни квадратного уравнения. Класс разбит на 3 группы, каждая группа получила задание.
Iгруппа Решение уравнений способом «переброски коэффициентов»
IIгруппа Решение уравнений способом «сложения коэффициентов»
III группа Решение уравнений по теорема Виета.
Затем работа плавно переход в « Снежный ком», где учащиеся группы перекомплектовались таким образом, что в каждой группе были участники с различными вопросами. Каждый ученик попробовал себя в роли «учителя»


«Ролевая игра» Идет обмен опытом и взаимообучение
3. Закрепление изученного материала. Группы комплектуются в первоначальные так, что теперь в каждой группе есть конспекты по всем видам уравнений с 5-11 класс. Ребята прорабатывают весь теоретический и материал и выполняют творческую работу: по каждому способу решения уравнения составить по 3 уравнения. Они с большим интересом работали в группах и индивидуально, выполняя задания непосредственно по своим зонам затруднения, одновременно развивая и совершенствуя творческие способности, логическое мышление. В конце урока выполнили «Итоговый тест». Качество 65,2%, Успеваемость - 100%

Такая форма работы РЦ с магнитными школами основанная на взаимном сотрудничестве, как отметили все учащиеся, очень удобна и имеет высокую эффективность.
Приложение к уроку.
1 блок
Тема: Уравнение
Микроцели - проанализировать линию решения уравнений по учебникам математики с 8 по 9 классы
- обобщить и систематизировать основные способы решения квадратных, биквадратных, дробно-рациональных уравнений
- устранение пробелов в знаниях
Деятельность учителя
Деятельность ученика
1. Объявить тему и цель урока
1. Ученики записывают тему в тетрадь
2. Мозговой штурм
а) что такое уравнение?
б) что называют корнем уравнения?
в) что значит решить уравнения?
г) какие виды уравнения вы знаете?
д) какие способы решения уравнений вы знаете?
3.Разбить учащихся на 3 малые группы
4. «Ожидания»
группам предлагается составить список того, что они ждут от урока
5. Работа в малых группах.
Раздать тест по теме « Уравнение»
( приложение № 1 «Входное тестирование»)
6. Ранжирование
( после составления схемы « Уравнение»)
7.Работа в малых группах
-
« Снежный ком»
Перекомплектовать группы таким образом, что в каждой группе были участники с различными вопросами.
-
Рефлексия:
( проверка по всему обобщающему материалу)
2. Отвечают на вопросы (устно)
4.Ожидания записывают на бумажке и каждая группа вывешивает свои листочки на доске в виде цветочка
5.
-
решить тест
-
проанализировать
-
составить структуру предложенных тестов
-
выявить проблемные зоны
-
составить план по ликвидации пробелов.
( Все идеи записываются на бумаге).
-
Каждая группа сообщает о своих результатах
6. «Уравнение»
- неполные
-
квадратные
-
биквадратные
-
дробно-рациональные
( Учащиеся выбирают тему для обсуждения)
7. Алгоритм деятельности группы
-
проработать учебники
-
записать план-конспект в тетрадь:
-
определения
-
способы решения
-
составить развивающие задачи по данному типу уравнений:
-
по аналогии
-
придумать свои примеры
8«Ролевая игра»
Идет обмен опытом и взаимообучение
9.Самостоятельная работа учащихся
(приложение №2. Тест № 2)
2 блок
.
Тема: Уравнение
Микроцели - способ сложения коэффициентов, способ переброски;
- ликвидация пробелов в знаниях
-
подготовка к ВОУД
Деятельность учителя
Деятельность ученика
-
Организационный момент (2 мин)
1. Учитель сообщает ученикам, в какой технологии будет построен урок, что на уроке будут выбраны «лучшие теоретики и практики»
-
Разбить класс на группы (19 мин)
Iгруппа Решение уравнений способом переброски коэффициентов
IIгруппа Решение уравнений способом сложения коэффициентов
III группа Решение уравнений по теорема Виета
-
Группы комплектуются в первоначальные так, что теперь в каждой группе есть конспекты по всем видам уравнений с 5-11 класс (10 мин)
-
Закрепление (10 мин)
-
Рефлексия (2 мин)
-
что я узнал нового ?
-
что я теперь смогу применить ?
-
над чем ещё надо работать ?
5 Итог урока : выставление оценок. (2 мин)
Домашняя работа
2. Работа аналогичная уроку I
а) каждая группа работает с раздаточным материалом, конспект
б) решают уравнения ( приложение 3)
3. Заполняется таблица до конца
4.Итоговый тест
(приложение№4)
5. Учащиеся отвечают на вопросы рефлексии (самостоятельно).
Тест (на входе)
по алгебре 9 класс
по теме «Квадратные уравнения»
Спецификация:
Цель тематического теста направлена на проверку знаний и умений, учащихся по теме «Квадратные уравнения».
.
Инструкция для обучающихся.
Заполните бланк тестирования, выбрав правильный ответ.
Бланк тестирования
Тест №_____
Фамилия_______
Имя______
Класс____
Балл Тестирования ___________
№ вопроса
1
2
3
4
5
6
7
Вариант ответа
Знать:
-
определение квадратного уравнения
-
формулу для вычисления дискриминанта
-
формулы для вычисления корней уравнения
-
теорему Виета
Уметь:
-
определять является уравнение квадратным
-
находить коэффициенты квадратного уравнения
-
решать квадратное уравнение преобразованием в квадрат двучлена
-
вычислять дискриминант
-
вычислять корни квадратного уравнения
-
применять теорему Виета
-
составлять уравнения по условию задачи
-
решать задачи на составление квадратных уравнений
Оценка:
8 баллов - «5»
6-7 баллов - «4»
4-5 баллов - «3»
менее 4 баллов - «2»
Входное тестирование
Тест по теме: «Квадратные уравнения»
1 вариант
-
Какое из данных уравнений не является квадратным?
а) 5х - х2 - 6 = 0; б) 3х2 + х = 4х - 2х2; в) 3 + х2 = 0; г) х2 = (х2-2)(х+1).
2. Найдите коэффициенты а, в, с квадратного уравнения: х - 3х2 +7 = 0.
а)1, -3, 7; б)-3, 1, 7; в) 0, -3, 7; г) другой ответ.
3. Выберите уравнение, дискриминант которого равен 49.
а) 8х2 + 3х + 2= 0; б) 2х2 -3х - 5 = 0; в) 3х2 - 3х - 7 = 0; г) 2х2 -3х + 1 = 0.
4. Решите уравнение 5х2 = 9х +2.
а) 2 и -0,2; б) 10 и -2; в) -2 и 0,2; г) другой ответ.
5. При каких значениях х верно равенство (2х - 3)2 = (х + 2)2?
а) 1/3 и -5; б) 5; в) -1/3 и -5; г) другой ответ.
6. При каком значении в уравнение 2х2 + вх - 10 =0 имеет корень 5?
а) 3; б) другой ответ; в) -3; г) -8.
7. Найдите сумму корней уравнения 6х2 - х + 12 = 0.
а) - 0,25; б) корнёй нет; в) 0,25; г) другой ответ.
8. Составьте уравнение по условию задачи.
Найдите два последовательных натуральных числа, произведение которых равно 272.
Входное тестирование
Тест по теме: «Квадратные уравнения»
2 вариант
1.Какое из данных уравнений является квадратным?
а) х(х2 - 1) = х2 - 2х; б) 7х + 9 = 0; в) 2х2 -3х = х + 5; г) 2/х2 = 3/х + 4х.
2. Найдите коэффициенты а, в, с квадратного уравнения: - х + 8 + 3х2 = 0.
а)3, 0, 8; б)-1, 3, 8; в) 3, -1, 8; г) другой ответ.
3. Выберите уравнение, дискриминант которого равен 25.
а) х2 + 3х +4 = 0; б) 2х2 +3х - 2 = 0; в) 16х2 - 3х = 0; г) 4х2 -3х + 1 = 0.
4. Решите уравнение 2х2 = 5х +3.
а) 3 и -0,5; б) корней нет; в) -3 и 0,5; г) другой ответ.
5. При каких значениях х верно равенство ( 3х +13)2 = ( 3 - 2х)2 ?
а) 5 и -0,2; б) 7; в) -16 и 7; г) другой ответ.
6. При каком значении в уравнение 3х2 + вх +24 =0 имеет корень 3 ?
а) 17; б) -17; в) -11; г) другой ответ.
7. Найдите произведение корней уравнения 2х2 - 9х + 5 = 0.
а) - 4,5; б) -2,5; в) 5; г) другой ответ.
8. Составьте уравнение по условию задачи.
Найдите два последовательных натуральных числа, произведение которых равно 210.
Итоговый тест по теме «Квадратные уравнения»
Пояснительная записка
Тесты являются одной из самых популярных форм контроля знаний учащихся. Они обеспечивают простоту проверки ответов учеников и позволяют выявить пробелы в их знаниях. Тесты - это достаточно краткие испытания и предназначены для того, чтобы оценить успешность овладения конкретными знаниями, как отдельных разделов программы, так и всего курса в целом (итоговые тесты). Грамотно составленные тесты являются объективными показателями обученности школьников.
Задания теста, составленные автором согласно теории по теме «Квадратные уравнения» в пределах учебного материала для учащихся 9 класса, предназначены для проверки уровня знаний, умений и навыков учащихся по данной теме и могут помочь выпускникам при подготовке к ВОУД и ЕНТ. При решении заданий данного итогового теста необходимо знать алгоритм нахождения количества корней квадратного уравнения, уметь решать полные и неполные квадратные уравнения и уравнения, сводящиеся к ним, уметь применять прямую и обратную теорему Виета. В тесте представлены два варианта, в каждом из которых шестнадцать заданий, и ответы к ним.
Итоговый тест: (на выходе)
Вариант 1
-
Найдите корни уравнения
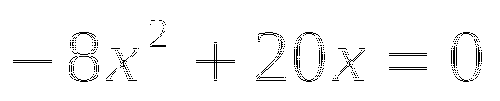
-
Решите уравнение
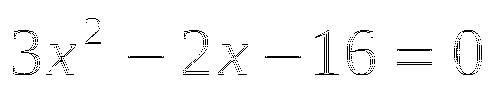
-
Найдите корни уравнения
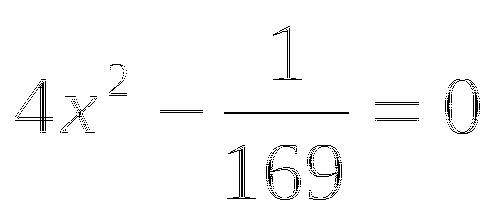
-
Из данных уравнений выберите то, которое имеет один корень
1. ![]() 2.
2. ![]() 3.
3. ![]() 4.
4. ![]()
-
Из данных уравнений выберите то, которое имеет два корня
1. ![]() 2.
2. ![]() 3.
3. ![]() 4.
4. ![]()
-
Из данных уравнений выберите то, которое не имеет корней
1. ![]() 2.
2. ![]() 3.
3. ![]() 4.
4. ![]()
-
Чему равна сумма корней уравнения
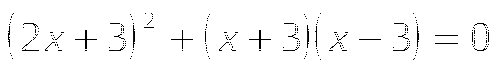 ?
?
8. Найдите произведение корней уравнения ![]()
9. Решите биквадратное уравнение ![]()
10. Найдите корни уравнений, используя теорему Виета ![]() -2х-24 = 0
-2х-24 = 0
11. Один из корней квадратного уравнения ![]() - 8
- 8![]() + q = 0 равен 9.
+ q = 0 равен 9.
Найдите коэффициент q.
12. Составьте квадратное уравнение, корни которого равны -25 и 8
13. Чему равна сумма квадратов корней уравнения ![]() ?
?
14. Сумма двух чисел равна -46, а их произведение равно -255.
Найдите модуль разности этих чисел.
15. Составьте квадратное уравнение, корни которого равны ![]() -2 и
-2 и ![]() -2
-2
16. При каком значении параметра k уравнение ![]() имеет 1 корень?
имеет 1 корень?
Итоговый тест: (на выходе)
Вариант 2
-
Найдите корни уравнения
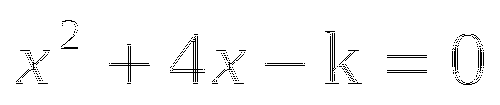
-
Решите уравнение
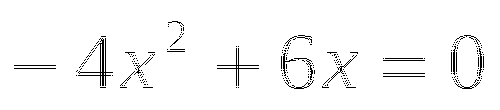
-
Найдите корни уравнения
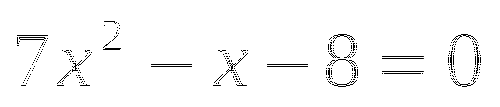
-
Из данных уравнений выберите то, которое имеет один корень
1. ![]() 2.
2. ![]() 3.
3. ![]() 4.
4. ![]()
-
Из данных уравнений выберите то, которое имеет два корня
1. ![]() 2.
2. ![]() 3.
3. ![]() 4.
4. ![]()
-
Из данных уравнений выберите то, которое не имеет корней
1. ![]() 2.
2. ![]() 3.
3. ![]() 4.
4. ![]()
-
Чему равна сумма корней уравнения
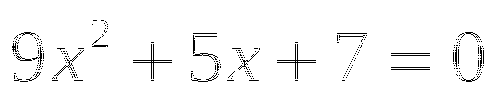 ?
?
8. Найдите произведение корней уравнения ![]()
9. Решите биквадратное уравнение ![]()
10. Найдите корни уравнений, используя теорему Виета ![]() -2х-63 = 0
-2х-63 = 0
11. Один из корней квадратного уравнения ![]() - 7
- 7![]() + q = 0 равен 11.
+ q = 0 равен 11.
Найдите коэффициент q.
12. Составьте квадратное уравнение, корни которого равны -45 и 6
13. Чему равна сумма квадратов корней уравнения ![]() ?
?
14. Сумма двух чисел равна -25, а их произведение равно -116.
Найдите модуль разности этих чисел.
15. Составьте квадратное уравнение, корни которого равны ![]() -4 и
-4 и ![]() -4
-4
16. При каком значении параметра k уравнение ![]() имеет 1 корень?
имеет 1 корень?
Ответы к тестам
-
Вариант 1
Вариант 2
№ п/п
верные ответы
№ п/п
верные ответы
1.
0; 2,5
1.
0; 1,5
2.
-2;
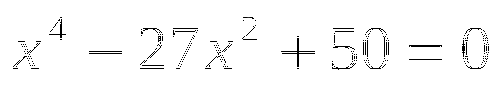
2.
-1;
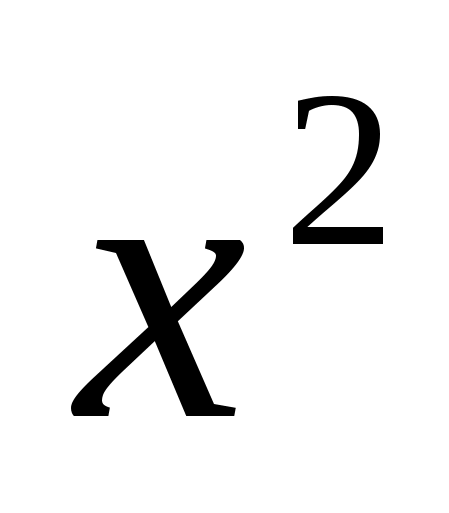
3.
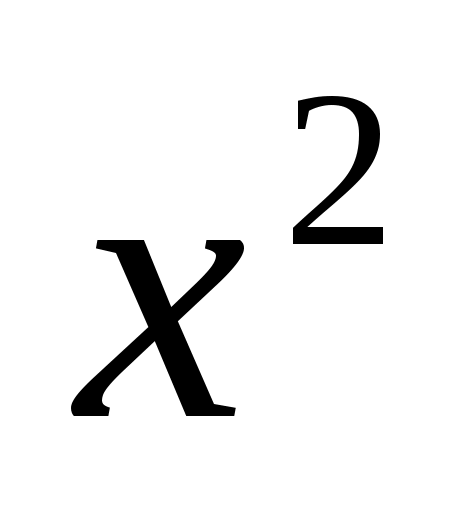 ;
; 
3.
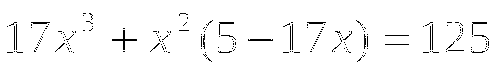 ;
;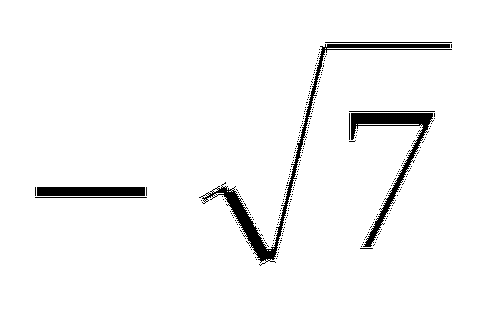
4.
4
4.
4
5.
3
5.
3
6.
2
6.
3
7.
-2,4
7.

8.
-81
8.
-4
9.
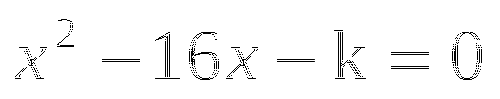
9.
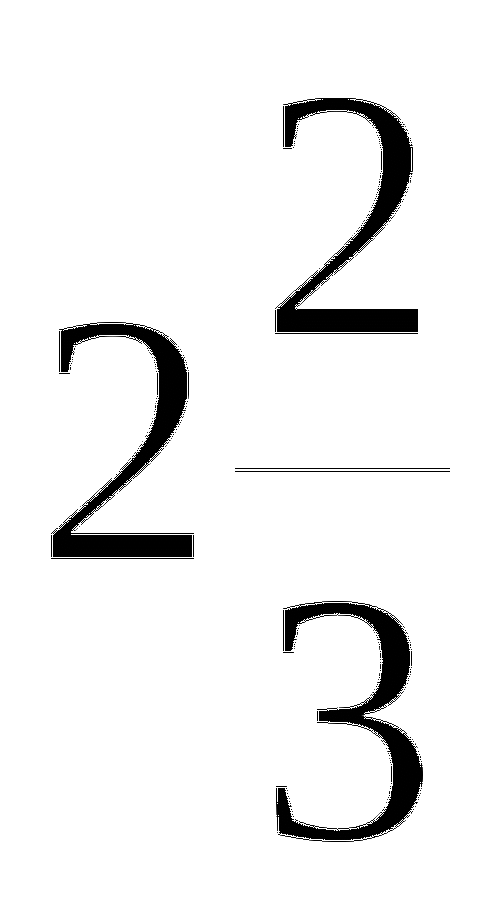
10.
-4; 6
10.
-7; 9
11.
-9
11.
-44
12.
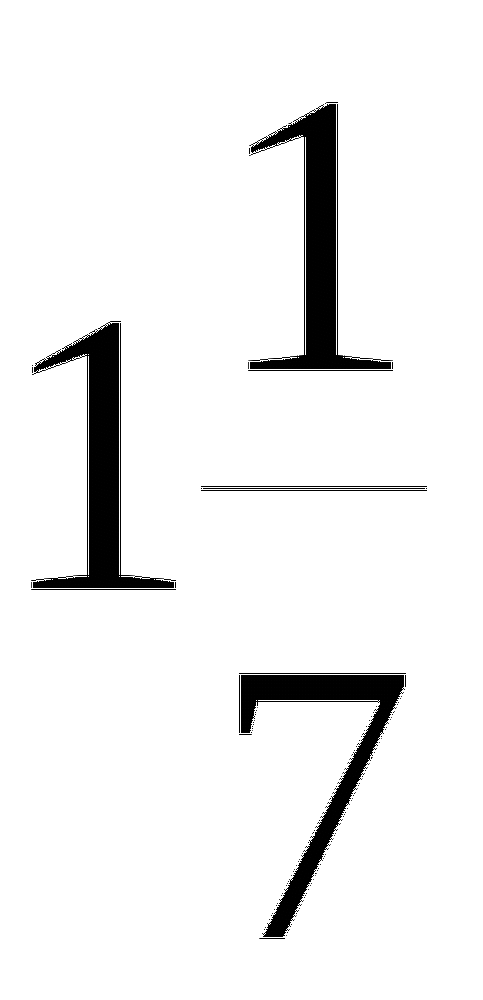
12.
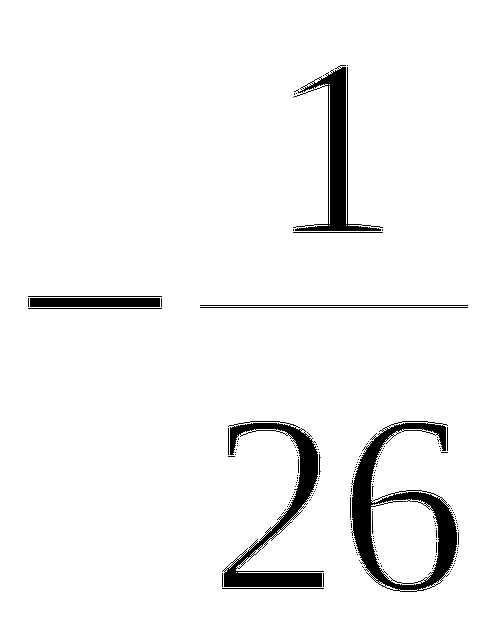
13.
8
13.
50
14.
56
14.
33
15.
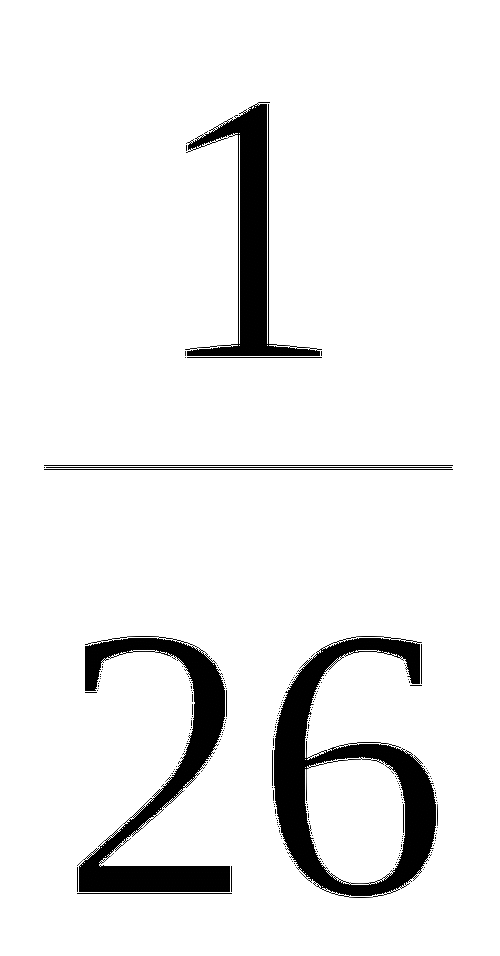
15.
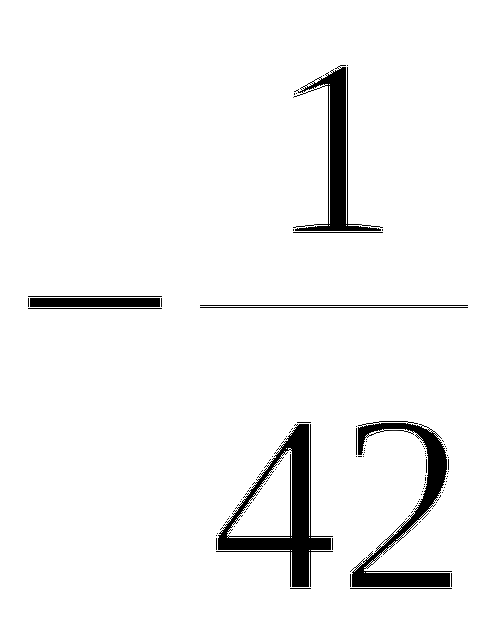
16.
-4
16.
-64
Приложение3.2
Решение уравнений с использованием теоремы Виета
(прямой и обратной)
1. Как известно, приведенное квадратное уравнение имеет вид
х2 + px + q = 0. (1)
Его корни удовлетворяют теореме Виета, которая при а = 1 имеет вид
![]()
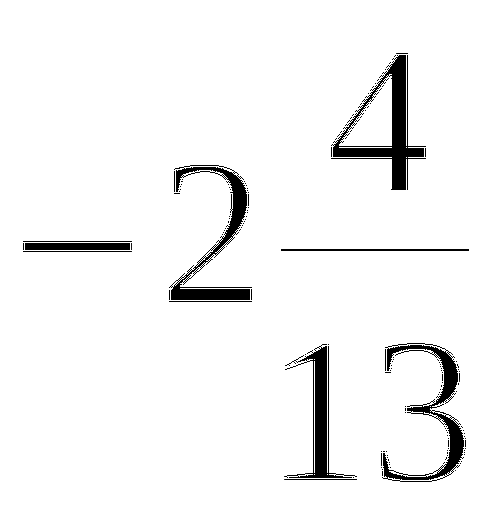
Отсюда можно сделать следующие выводы (по коэффициентам p и q![]() можно предсказать знаки корней).
можно предсказать знаки корней).
а) Если свободный член q![]() приведенного уравнения (1) положителен (q >0), то уравнение имеет два одинаковых по знаку корня и это зависит от второго коэффициента p.
приведенного уравнения (1) положителен (q >0), то уравнение имеет два одинаковых по знаку корня и это зависит от второго коэффициента p.
Если p>0, то оба корня отрицательные, если p<0, то оба корня положительны.
Например,
х2 - 3х + 2 = 0; х1 = 2 и х2 = 1, так как q = 2 > 0 и p = - 3 <0;
х2 +8х + 7 = 0; х1 = - 7 и х2 = - 1, так как q = 7 > 0 и p = 8 >0.
б) Если свободный член q![]() приведенного уравнения (1) отрицателен (q < 0), то уравнение имеет два различных по знаку корня, причем больший по модулю корень будет положителен, если p<0, или отрицателен, если p>0.
приведенного уравнения (1) отрицателен (q < 0), то уравнение имеет два различных по знаку корня, причем больший по модулю корень будет положителен, если p<0, или отрицателен, если p>0.
Например,
х2 + 4х - 5 = 0; х1 = - 5 и х2 = 1, так как q = - 5<0 и p = 4 > 0;
х2 - 8х - 9 = 0; х1 = 9 и х2 = - 1, так как q = - 9<0 и p = - 8 >0.
2. Теорема Виета для квадратного уравнения
ах2 +вх +с = 0
имеет вид
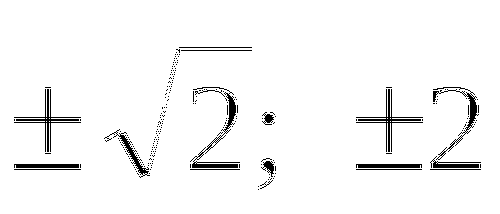
3. Справедлива теорема, обратная теореме Виета:
Если числа х1 и х2 таковы, что х1+х2 = -р, х1х2 = q, то х1 и х2 - корни квадратного уравнения
х2 +рх + q = 0.
Эта теорема позволяет в ряде случаев находить корни квадратного уравнения без использования формулы корней.
● Примеры
1. Решить уравнение
х2 - 9х + 14 =0
Попробуем найти два числа х1 и х2 , такие, что
х1 +х2 = 9
х1х2 = 14
Такими числами являются 2 и 7. По теореме, обратной теореме Виета, они и служат корнями заданного квадратного уравнения.
2. Решить уравнение
х2 +3х - 28 = 0
Попробуем найти два числа х1 и х2 , такие, что
х1 +х2 = - 3
х1х2 = - 28
Нетрудно заметить, что такими числами будут - 7 и 4. Они и являются корнями заданного уравнения.
3. Составить уравнения по теме (по5 примеров)
Приложение 3.1
Решение уравнений способом «переброски»
Рассмотрим квадратное уравнение
ах2 + bх + с = 0, а ≠ 0.
Умножая обе его части на а, получаем уравнение
а2 х2 + а bх + ас = 0.
Пусть ах = у, откуда х = ![]() ; тогда приходим к уравнению
; тогда приходим к уравнению
у2 + by + ас = 0,
равносильного данному. Его корни у1 и у2 найдем с помощью теоремы Виета. Окончательно получаем х1 = ![]() и х1 =
и х1 = ![]() . При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его и называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.
. При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его и называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.
● Примеры
1. Решим уравнение 2х2 - 11х + 15 = 0.
Решение. «Перебросим» коэффициент 2 к свободному члену, в результате получим уравнение
у2 - 11y +30 = 0.
Согласно теореме Виета
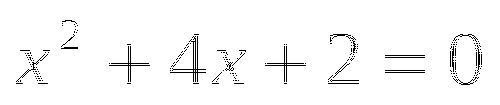 Ответ: 2,5;3.
Ответ: 2,5;3.
2. Составить уравнения по теме (по5 примеров)
Приложение 3.3
Свойства коэффициентов квадратного уравнения
А. Пусть дано квадратное уравнение
ах2 + bх + с = 0, а ≠ 0.
1.Если а + b + с = 0 (т.е. сумма коэффициентов уравнения равна нулю), то х1 = 1, х2 = ![]() .
.
Доказательство. Разделим обе части уравнения на а ≠ 0, получим приведенное квадратное уравнение
х2 + ![]() х +
х + ![]() = 0.
= 0.
Согласно теореме Виета
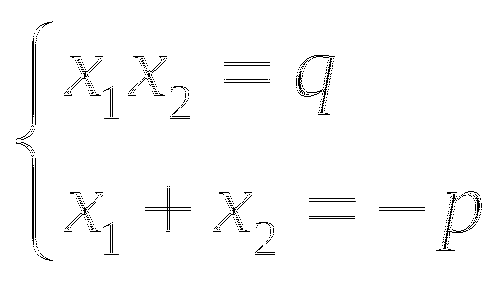
По условию а + b + с = 0, откуда b = - а - с. Значит,

Получаем х1 = 1, х2 = ![]() , что и требовалось доказать.
, что и требовалось доказать.
2. Если а - b + с = 0, или b = а + с, то х1 = - 1, х2 = - ![]() .
.
Доказательство. По теореме Виета
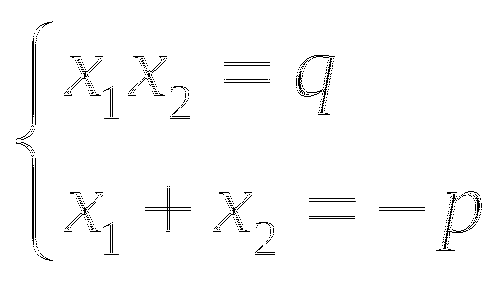
По условию а - b + с = 0, откуда b = а + с. Таким образом,

т.е. х1 = - 1 и х2 = ![]() , что и требовалось доказать.
, что и требовалось доказать.
● Примеры
1. Решим уравнение 345х2 -137х - 208 = 0.
Решение. Так как а + b + с = 0 (345 - 137 - 208 = 0), то х1 = 1, х2 = ![]() =
= ![]() .
.
Ответ: 1; - ![]() .
.
2. Решим уравнение 132х2 + 247х + 115 = 0
Решение. Т. к. а-b+с = 0 (132 - 247 +115=0), то
х1= - 1, х2= - ![]()
Ответ: - 1; - ![]()
Б. Если второй коэффициент b = 2k - четное число, то формулу корней
х1,2 = ![]()
можно записать в виде
х1,2 = ![]()
● Пример
3. Решим уравнение 3х2 -14х + 16 = 0.
Решение. Имеем: а = 3, b = - 14, c = 16, k = - 7;
D = k2 - ac = (- 7)2 - 3 · 16 = 49 - 48 = 1, D>0, два различных корня;
х = ![]()
Ответ: 2; ![]() .
.
В. Приведенное уравнение
x2 + px + q = 0
совпадает с уравнением общего вида, в котором а = 1, p и c = q. Поэтому для приведенного квадратного уравнения формула корней
х1,2 = ![]()
принимает вид:
х1,2 = ![]() или х1,2 = -
или х1,2 = -  (3).
(3).
Формулу (3) особенно удобно использовать, когда p - четное число.
● Примеры
4. Решим уравнение х2 -14х - 15 = 0.
Решение. Имеем: х1,2 = 7±![]() = 7±
= 7±![]() = 7±8. Ответ: х1 = 15, х2 = - 1 .
= 7±8. Ответ: х1 = 15, х2 = - 1 .
Г). Составить уравнения по теме (по5 примеров)