Урок по математике для 6 класса 'Сложение отрицательных чисел'

Конспект урока по математике.

Тема урока: «Сложение отрицательных чисел».

Цели урока:

• Образовательная: формирование у учащихся умения осуществлять сложение отрицательных чисел; вывод с учащимися правила сложения отрицательных чисел; формирование у учащихся умения применять данное правило на практике; обучение учащихся правильному чтению и записи примеров с отрицательными числами.

• Развивающая: развитие наблюдательности, логического мышления, памяти, внимания и мышления учащихся, а также развитие у них вычислительных навыков.

• Воспитательная: воспитание у учащихся умения работать в коллективе, дисциплинированности на уроке; воспитание интереса к предмету, аккуратности и точности при построении чертежей на доске и в тетрадях.

Методы обучения: индуктивно-эвристический, дедуктивно-репродуктивный.

Тип урока: урок изучения нового материала.

Требования к ЗУН:

учащиеся должны знать:

• определение понятия модуля числа;

• алгоритм нахождения модуля числа;

• правило сложения чисел а и b;

• определение понятия отрицательного числа;

• правило сложения отрицательных чисел;

учащиеся должны уметь:

• складывать модули чисел;

• правильно читать и записывать примеры с отрицательными числами;

• складывать отрицательные числа;

• применять правило сложения отрицательных чисел на практике.

Литература:

• Виленкин Н. Я., Жохов В. И.. Чесноков А. С., Шварцбурд С. И. «Математика: учеб, для 6 кл. общеобразоват. учреждений» М.: Мнемозина, 2005. -288 с.

• Методические рекомендации к учебнику Математика. 6 кл.: учеб, для общеобразоват. учреждений / Виленкин Н. Я.. Жохов В. И.. Чесноков А. С., Шварцбурд С. И.

• Саранцев Г.И. «Методика обучения математики в средней школе.: учеб, пособие для студентов мат. спец. педвузов и унив.» М.: Просвещение, 2002. - 224 с.

План урока

1. Организационный момент (1 минута);

2. Актуализация знаний (5 минут);

3. Сообщение темы урока, постановка целей урока (1 минута);

4. Изучение нового материала (15 минут);

5. Первичное закрепление изученного материала (20 минут);

6. Подведение итогов (2 минуты);

7. Домашнее задание (1 минута).

ХОД УРОКА

1. Организационный момент

Приветствие учеников, проверка отсутствующих, проверка готовности помещения к уроку.

2. Актуализация знаний

Учитель: итак, на прошлом уроке мы закончили изучение темы «Сложение чисел с помощью координатной прямой». Сейчас я предлагаю двоим ученикам выполнить задание, записанное на доске, а все остальные в это время устно отвечают на вопросы.

Учащиеся у доски объясняют по одному примеру:

Ученик: Чтобы к -2 прибавить -2 нужно из точки с координатой -2 переместиться на две единицы влево, и мы попадем в точку с координатой -4

Ученик: Чтобы к -3 прибавить -2 нужно из точки с координатой -4 переместиться на две единицы влево и мы попадем в точку -5.

Запись на доске: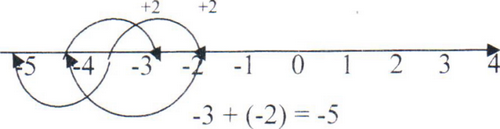

-2 + (-2) = -4

Остальные учащиеся отвечают на вопросы с места:

Учитель: Что значит прибавить к числу а число b?

Ученик: Прибавить к числу а число b, значит изменить число а на b единиц

Учитель: Если к числу а прибавить число b, как изменится число а, при условии, что , b - положительное; отрицательное; ноль?

Ученик: Если число b положительное, то число а увеличится на b единиц, если число b отрицательное, то число а уменьшится на b единиц, если b равно нулю, то число а не изменится

Учитель: Чему равна сумма двух противоположных чисел?

Ученик: Сумма двух противоположных чисел равна нулю.

3. Сообщение темы урока, постановка целей.

Учитель: А теперь откроем тетради, запишем число, классная работа, и тему нашего сегодняшнего урока «Сложение отрицательных чисел».

Запись на доске и в тетрадях:

Классная работа.

Сложение отрицательных чисел.

Учитель: Изучив сложение чисел с помощью координатной прямой, вы уже умеете складывать отрицательные числа. Сегодня на уроке мы научимся складывать отрицательные числа, не обращаясь к координатной прямой, и выведем правило сложения отрицательных чисел.

4. Изучение нового материала

Учитель: Сегодня мы уже складывали два отрицательных числа. Посмотрите на доску. Мы к -2 прибавили -2. Что мы сделали для этого?

Ученик: Мы переместились из точки с координатой -2 на две единицы влево и попали в точку с координатой -4.

Учитель: Но пользоваться всякий раз. Когда нам нужно сложить числа, координатной прямой неудобно. Например, если нам потребуется сложить числа -650 и -8.53. поэтому рассмотрим, как находить сумму двух чисел, не обращаясь к координатной прямой.

Учитель: Давайте сложим числа -3 и -5, не изображая их на координатной прямой, но представляя себе эту прямую. Сколько получилось?

Ученик: -8

Учитель: Правильно. Теперь рассмотрим, как это получилось. Чтобы найти сумму этих чисел, надо из числа -3 переместиться на пять единиц влево, ясно, что полученное число будет дальше от нуля, чем -3, то есть будет отрицательным числом, удаленным от нуля на 3 + 5 = 8 единиц. То есть сумма -3 и -5 есть число отрицательное, равное -8. Запишите данный пример себе в тетрадь.

Учитель записывает этот пример на доске.

Запись на доске и в тетрадях:

-3 + (-5) = -8

Учитель: рассмотрим еще один пример: -8.63 + (-1.37), мысленно перемещаем точку с координатой -8.63 влево, какое число получится?

Ученик: Отрицательное! -10!

Учитель: Отлично. Может быть кто-то сможет сформулировать правило сложения двух отрицательных чисел самостоятельно?

Ученик: чтобы сложить два отрицательных числа, нужно сложить их модули и перед результатом поставить знак минус.

Учитель: верно. Это правило вы найдете в учебнике на странице 174. Пожалуйста, запишите его в тетрадь для лучшего запоминания.

Запись в тетрадях:

Чтобы сложить два отрицательных числа, нужно сложить их модули и перед суммой поставить знак минус.

5. Закрепление первичного материала

Учитель: А теперь давайте устно решим № 1043 (а).

Ученик: -2 + (-5). Число будет лежать слева от нуля, то есть будет отрицательным, модуль числа -2 равен 2, модуль числа -5 равен 5, 2 + 5 = 7, ставим знак минус, получим - 7. Учитель: Следующий № 1045 (а)

Ученик делает у доски задание и комментирует его:

Ученик: Чтобы сложить числа -35 и -9, нужно сложить их модули, 35 и 9, и перед суммой поставить знак минус, получим число -44.

Запись на доске и в тетрадях:

-35 + (-9) = -(35 + 9) = -44

Учитель: Что называют модулем числа?

Ученик: Модулем числа называют расстояние от точки А с координатой а до начала координат, выраженное в единичных отрезках.

Учитель: Может ли модуль числа быть отрицательным?

Ученик: Нет, модуль числа - число, всегда положительное.

Учитель: Следующий № 1046. Поставьте вместо * знак < (больше) или > (меньше), чтобы равенство стало верным.

Ученики по очереди выходят к доске, делают задания и комментируют их:

Ученик: Первое действие - сложение чисел, стоящих слева от звездочки:

1. -17 + (-31) = -(17 + 31) = -48

Ученик: Второе и третье действия - нахождение модулей чисел -48 и -17:

2. |-48 | = 48

3. | -17 | = 17

Ученик: Потом мы сравниваем модули чисел: 17 < 48:

• 17 <48

Ученик: И применяем правило сравнения отрицательных чисел - из двух отрицательных чисел больше то, модуль которого меньше, то есть -17 > -48:

• -17 >-48

Запись на доске и в тетрадях:

а) -17+ (-31)* -17; |-48 | = 48; |-17 | = 17; 17 < 48;-17 >-48;-17 + (-31) <-17.

Следующий пример решается аналогично.

Запись на доске и в тетрадях:

б) -22+ (-35) * -35; -22 + (-35) = - (22 + 35) = -57; | -57 | = 57; | -35 | = 35; 57 > 35; -57 < -35.

Учитель: Следующий № 1048 (а).

Ученик делает у доски задание и комментирует его:

Ученик: Будем решать по действиям. Первое действие - сложим числа в первой скобке, для этого сложим их модули и поставим перед суммой знак минус:

• -0.251 +(-0.37) = -(0.251 + 0.37) = -0.621

Ученик: Второе действие - сложим числа во второй скобке так же, как и в первой:

• -0.2 + (-0.152) = - (0.2 + 0.152) = - 0.352

Ученик: Третье действие - сложим полученные в первом и втором действии результаты и получим ответ:

• -0.621 + (-0.352)= -(0.621 + 0.352)= - 0.973

Запись на доске и в тетрадях:

(-0.251+ (-0.37)) + (-0.2 + (-0.152)) = -0.973

1. -0.251 + (-0.37) = - (0.251 + 0.37) = - 0.621

2. -0.2 + (-0.152) = - (0.2 + 0.152) = - 0.352

3. -0.621 + (-0.352)= -(0.621 + 0.352)= - 0.973

Учитель: Сейчас решим № 1052 по цепочке, начиная с первого ряда, с объяснением:

Учащиеся по очереди, начиная с первого ряда, комментируют решение примеров данного номера.

Ученик: 0 и х, так как х положительное, то оно всегда больше нуля

Ученик: -у и 0, так как у положительное, то -у отрицательное, значит -у меньше нуля, так как отрицательное число всегда меньше нуля

Ученик: -х и у. так как х положительное, то -х отрицательное, у положительное, любое положительное число всегда больше отрицательного, значит -х меньше у

Ученик: | х | и -х, модуль всегда положительный, -х число отрицательное, положительное число всегда больше отрицательного, следовательно модуль х больше, чем -х

Ученик: | у | и у, у число положительное, модуль у тоже число положительное, равное у, значит модуль у и у равны

Ученик: -х и | у |. -х отрицательное, модуль у положительное, следовательно модуль у больше, чем -х

Ученик: | -х | и -у, -х число отрицательное, модуль отрицательного числа - число положительное, -у число отрицательное, значит модуль -х больше, чем -у

Учитель: теперь № 1051 выполните самостоятельно, а потом мы вместе проверим правильность выполнения.

Ученики выполняют, все вместе делают проверку:

Учитель: расположите числа в порядке убывания:

Ученик:-5.5 ; 3 ; 1 ; 2/3 ; 0 ; -2/7 ; -3/5 ; -8.2 ; -8.8 ; -10 2/7 ; -10 3/7 ; -15.

Учитель: допущена ошибка, кто исправит?

Ученик: 3 ; 1 ; 2/3 ; 0 ; -2/7 ; -3/5 ; -5.5 ; -8.2 ; -8/8 ; - 10 2/7 ; -10 3/7; -15.

Учитель: это верный ответ; исправьте, у кого не так.

6. Подведение итогов

Учитель: Что нового вы сегодня узнали?

Ученик: Что сумма двух отрицательных чисел отрицательное число.

Ученик: Чтобы сложить два отрицательных числа, нужно сложить их модули и перед суммой поставить знак минус.

Учитель: А у меня к вам вопрос на сообразительность. Может ли при сложении отрицательных чисел получится ноль? Ответ обоснуйте.

Ученик: Нет, не может. При сложении отрицательных чисел может получиться только отрицательное число, а ноль - не отрицательное число. К тому же мы знаем, что ноль получается при сложении противоположных чисел, а из них одно всегда положительное.

Учитель: верно. Итак, сегодня на уроке вы хорошо поработали, почти все были активны, что позволило нам решить много заданий.

7. Домашнее задание

Учитель: Теперь запишите домашнее задание. П. 32 - выучить правило. №№ 1056 (а - г), 1057 (а), 1058. Спасибо, можете быть свободны.