Проект 'Геометрические соотношения танграм' (8 класс)

Китайская головоломка

"ТАНГРАМ"

пособие для начинающих

2013

Содержание

1. Что такое "Танграм"

2

2. Правила игры

3

3. Соотношения сторон и размеры углов танов

4

4. Соотношения площадей танов

5

5. Как собрать фигуру?

6

6. Первые шаги к успеху

7

7. Сделай сам

8

8. Ответы

10

Танграм - головоломка, состоящая из семи плоских фигур "танов": квадрата, параллелограмма, двух больших одинаковых треугольников, среднего треугольника и двух одинаковых маленьких треугольников.

Изготовление танграма.

Возьмите лист картона 10см×10см. Разрежьте следующим образом.

P

K

C

E

D

M

F

B

А

O

Ответы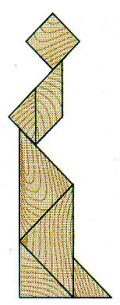

Правила игры

• В каждую фигуру должны входить все семь деталей.

• Фигуры должны соприкасаться между собой (не должны перекрываться).

• Начинать нужно с того, чтобы найти место двух самых больших треугольников.

• Далее определять место танов по убыванию площадей.

• Убедитесь, что собранная фигура в точности копирует силуэт.

• Собрав одну фигуру, соберите другую.

Желаем удачи!

Соотношение сторон и размеры углов танов:

• Длина катета большого треугольника равна длине гипотенузы среднего треугольника.

• Длина катета среднего треугольника равна длине гипотенузы маленького треугольника, диагонали квадрата и одной из сторон параллелограмма.

• Длина катета маленького треугольника равна длине стороны квадрата и другой стороны параллелограмма.

• У параллелограмма два угла по 45˚ и еще два по 135˚.

• Пять треугольников равнобедренные и прямоугольные, поэтому у каждого из них есть угол в 90˚ и два угла по 45˚.

• У квадрата, разумеется, четыре угла по 90˚.

Сделай сам

7

8

9

10

11

12

Сделай сам

1

2

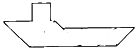
3

4

5

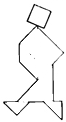6

Соотношение площадей:

• Площадь большого треугольника вдвое больше площади среднего треугольника.

• Средний треугольник, квадрат и параллелограмм имеют одинаковую площадь.

• Площадь среднего треугольника вдвое больше площади маленького треугольника.

• Площадь квадрата вдвое больше площади маленького треугольника.

• Площадь параллелограмма вдвое больше площади маленького треугольника.

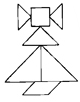
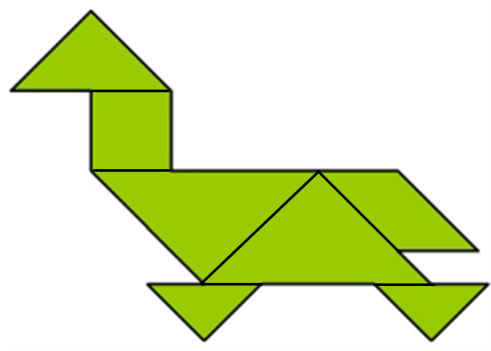
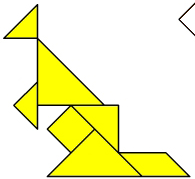
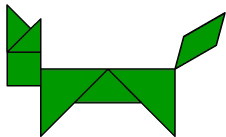
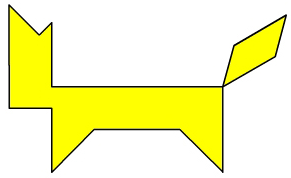
Как собрать фигуру?

В наборе семь фигур (танов): квадрат, параллелограмм, два больших треугольника, один средний треугольник и два маленьких треугольника. Замечаем, что самое большое по площади место -

это туловище, размещаем там два больших треугольника. (рис.1) Далее видно: "хвост" - место среднего треугольника, а "ноги" - маленького треугольника. Остались три тана: параллелограмм, квадрат и маленький треугольник. Размещаем: "шея" - параллелограмм (рис. 2), "голова" - квадрат и "клюв" - второй маленький треугольник. (рис. 3)

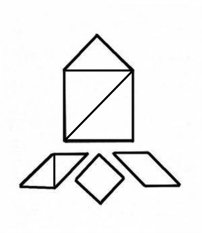
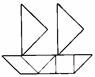
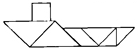
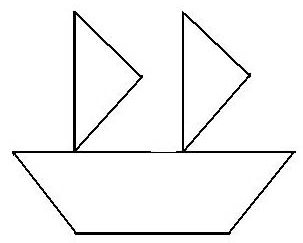
Первые шаги к успеху

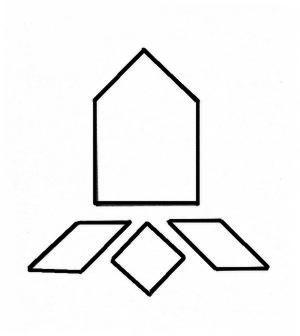
Начинаем с больших треугольников. Несомненно, один расположен на _______ домика (рис.1), а второй может поместиться только внутри.

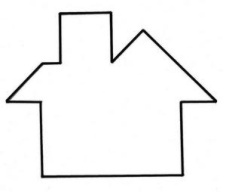
Но как именно? Замечаем, что "высота стен домика" меньше, чем "скос крыши". Значит, второй большой треугольник не может располагаться прямым углом к "стене" и "полу". Следовательно, он может вместиться только прямым углом ________ или ________ .(рис.2) Достраивая "стены", видно, что с одной стороны от треугольника вмещается один __________ треугольник, а с другой, составленная из двух __________ треугольников, равная фигура по площади.(рис.3) Труба имеет форму ________, поэтому там будет располагаться _________.(рис.4) Остальное место на крыше подходит только для оставшейся фигуры.