Конспект урока по алгебре на тему Графическое решение уравнений (7 класс)

Муниципальное бюджетное государственное образовательное учреждение «Ангарский лицей №1»

Конспект урока по алгебре

Графическое решение уравнений

7 класс

Учитель математики

Никифорова С.В.

г.Ангарск, 2012г.

Цель урока: Составить алгоритм графического решения уравнений и учиться применять его на практике

Задачи урока:

• уточнить понятие уравнения;

• повторить виды уравнений и алгоритмы их решения;

• повторить изученные ранее функции;

• развивать алгоритмическое мышление;

• воспитывать интерес к участию в поисковой деятельности.

Оборудование и материалы:

• проектор, интерактивная доска;

• презентация по теме;

• Мордкович, А. Г. Алгебра. 7 класс : в 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович. - М. : Мнемозина, 2015.

• Алгебра. 7 класс : в 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович [и др.]; под ред. А. Г. Мордковича. - М.: Мнемозина, 2015.

• карточки со справочным материалом;

• бланки для самостоятельной работы;

• карта оценки деятельности на уроке.

План урока:

1. Подготовительный этап

Цель - настроить на работу

2. Актуализация знаний

Цель - повторить виды уравнений, алгоритмы их решения, виды функций, их графики

3. Изучение новой темы

Цель - разработать алгоритм графического решения уравнений

3. Решение задач (№№ 35.4(а, г), 35.5(а, в), 35.8 (а, г))

Цель - первичное закрепление алгоритма графического решения уравнений

3. Самостоятельная работа

Цель - первичный анализ усвоения алгоритма графического решения уравнений

3. Подведение итогов урока, рефлексия.

Цель - проанализировать успехи и неудачи работы на уроке

3. Домашнее задание:

1. § 33, выучить алгоритм графического решения уравнений

2. Решить задачи №№ 35.6(б, г), 35.7(а, б), 35.10(а, б), 35.13(а)

3. По желанию: подобрать и решить три уравнения различной сложности, которые можно решить с помощью графиков

На первый взгляд, понятие не ново,

И не всегда подумаешь о том,

Как важно будет в жизни это слово

И сколько смысла будет в слове том!

По - разному с годами толковали.

Сам Лобачевский руку приложил,

Чтоб слово «функция» и в средней школе знали,

Чтоб каждый ученик им дорожил!

Без функции не сдашь простой экзамен,

Без функции ты не войдешь в предмет!

Без функции не разгорится пламя!

Без функций никакой науки нет!

И Кушнир, Л. Финкельштейн. «Ода функции»

I. Подготовительный этап

Цель - настроить на работу, сообщить тему урока, цель урока

II. Актуализация знаний

Цель - повторить виды уравнений, алгоритмы их решения, виды функций, их графики

1. Дайте общее название записям на доске:

2. Что такое уравнение? Что называется корнем уравнения? Как проверить, будет ли данное число корнем уравнения?

3. Распределите уравнения на 2 группам, укажите признак разбиения.

Линейные

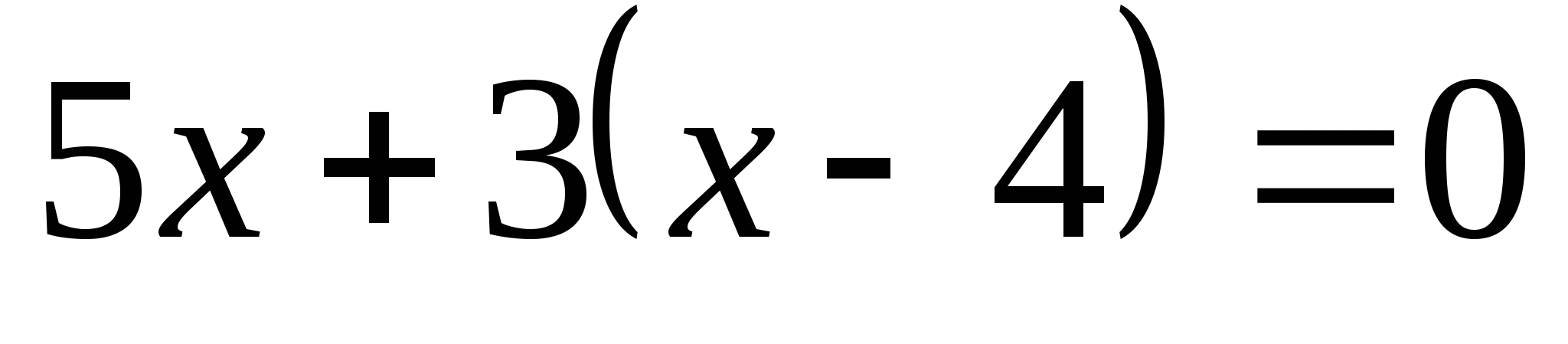
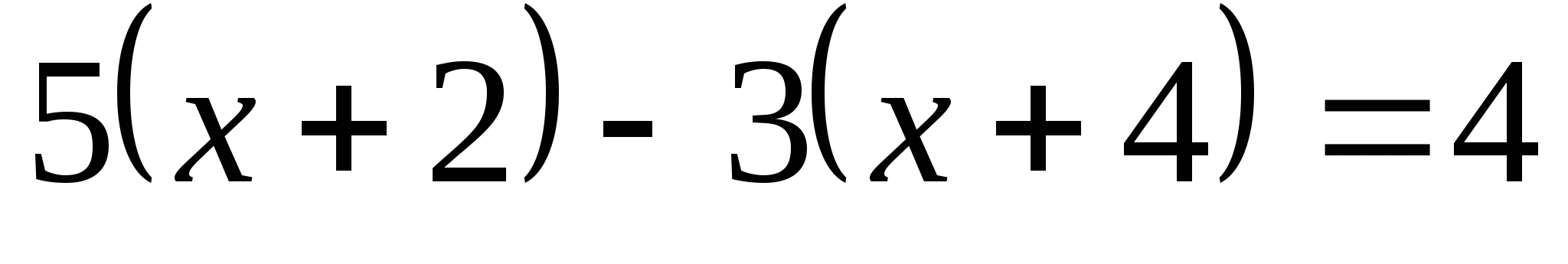
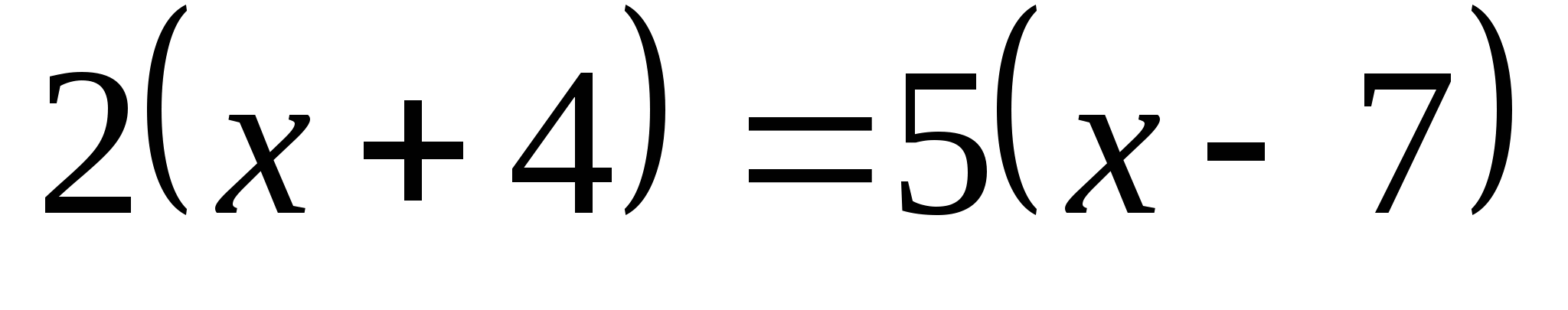
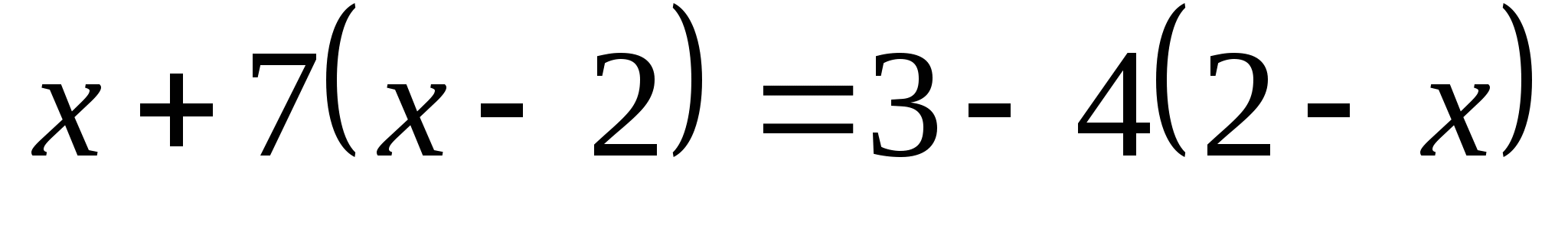
Нелинейные

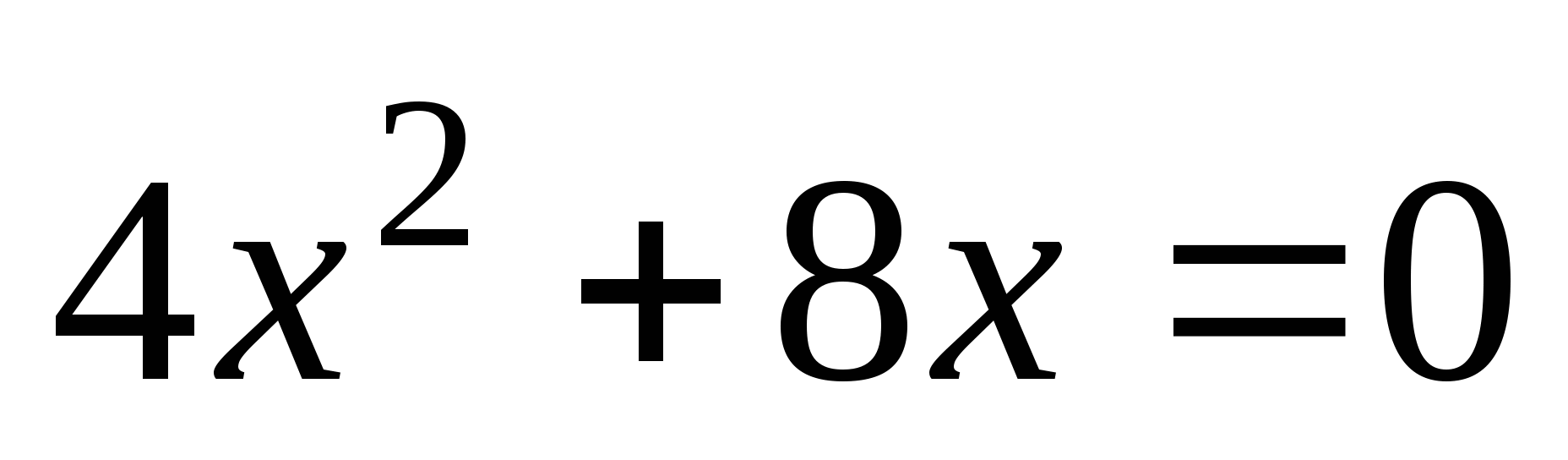
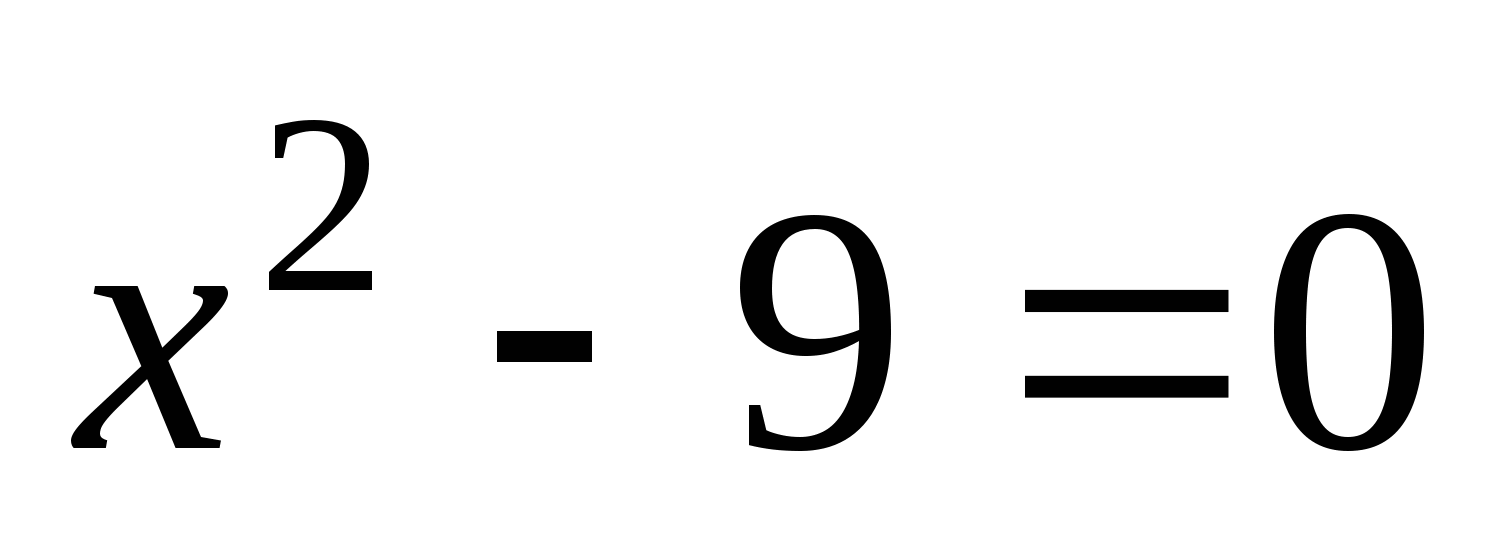
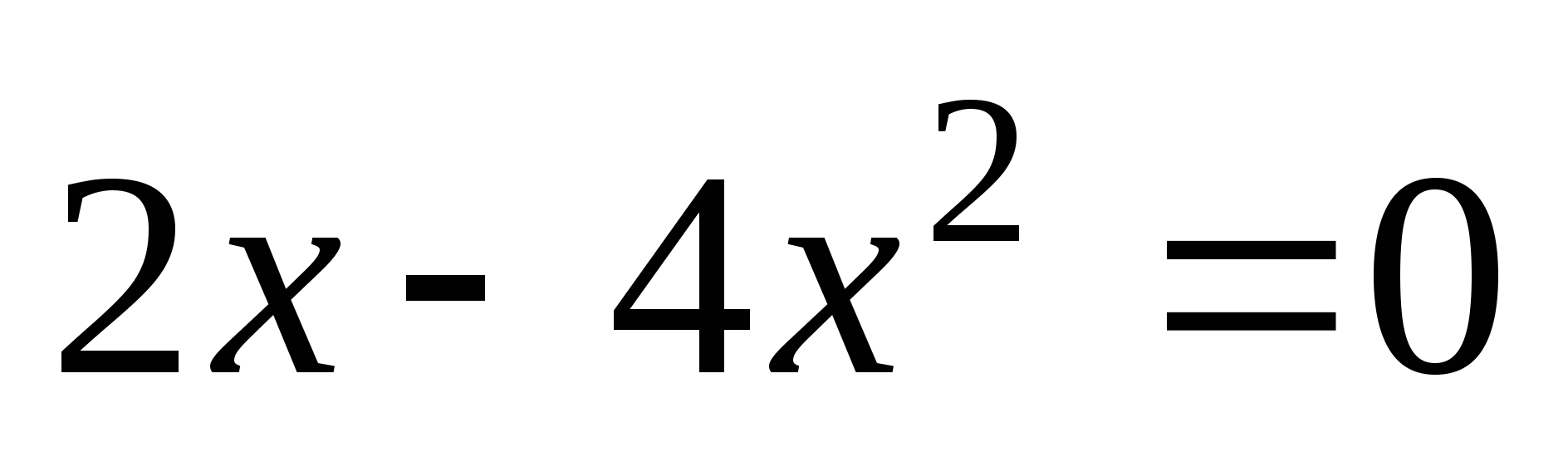
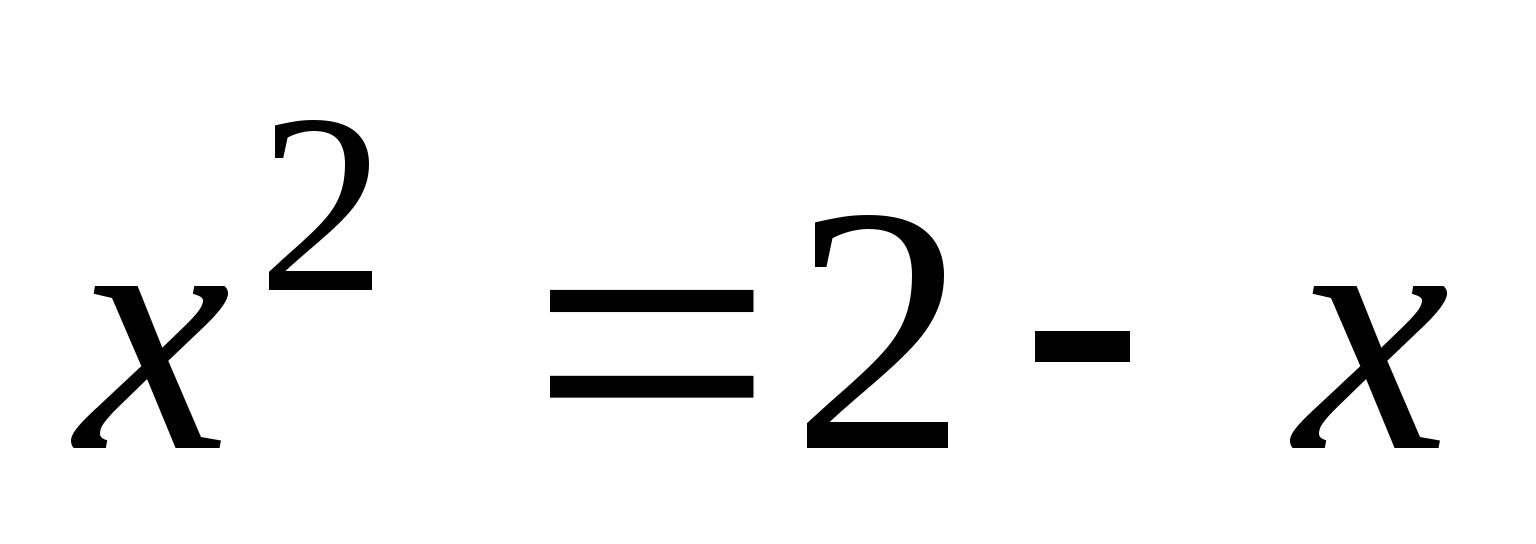
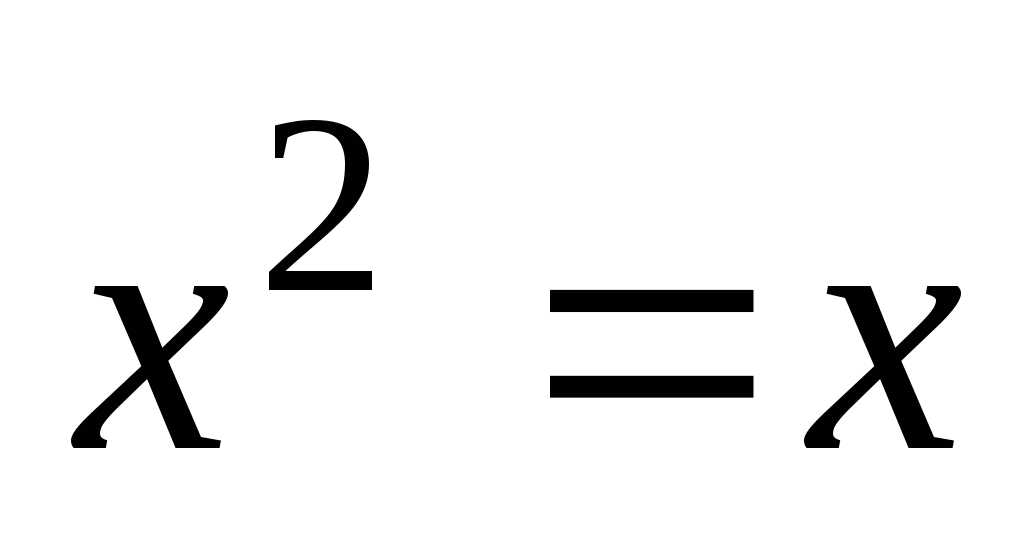
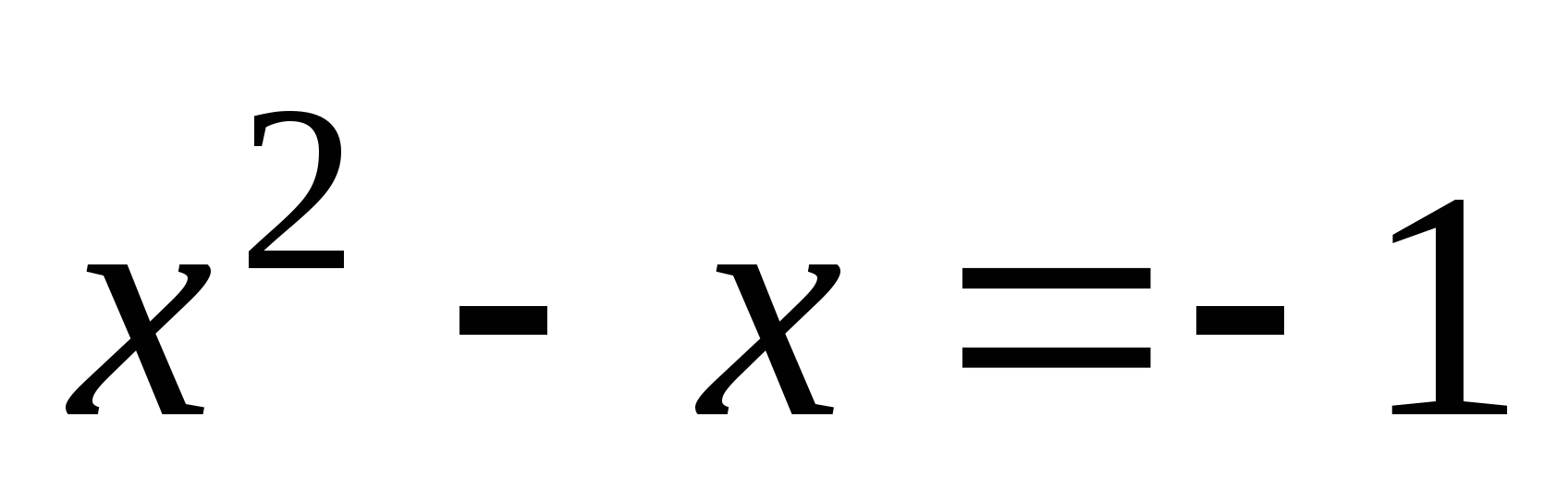
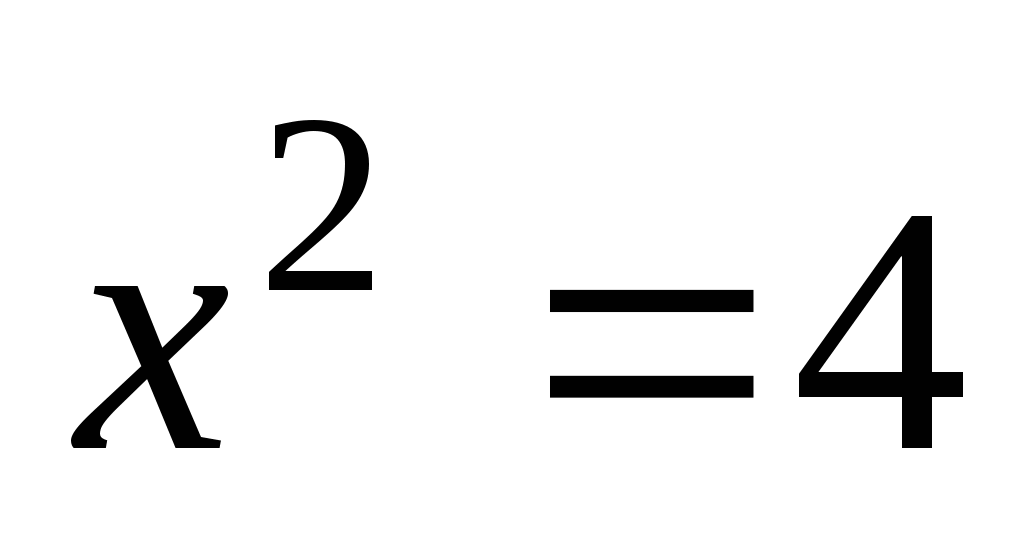
4. Повторить алгоритм решения линейного уравнения.

5. С какими видами нелинейных уравнений мы уже встречались?

; ; ; ;

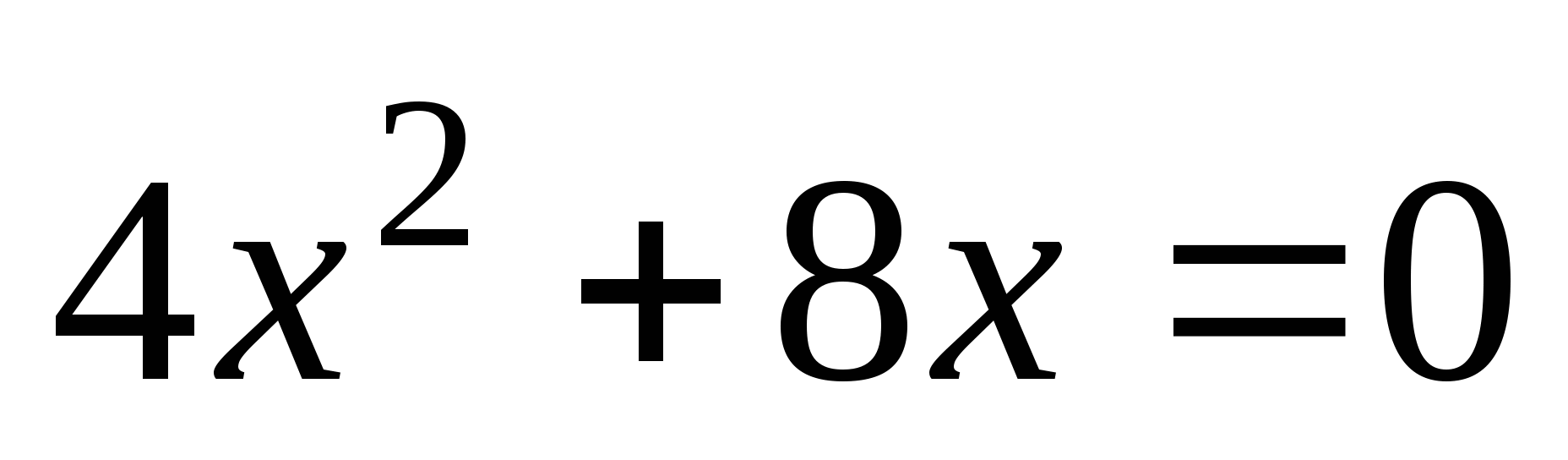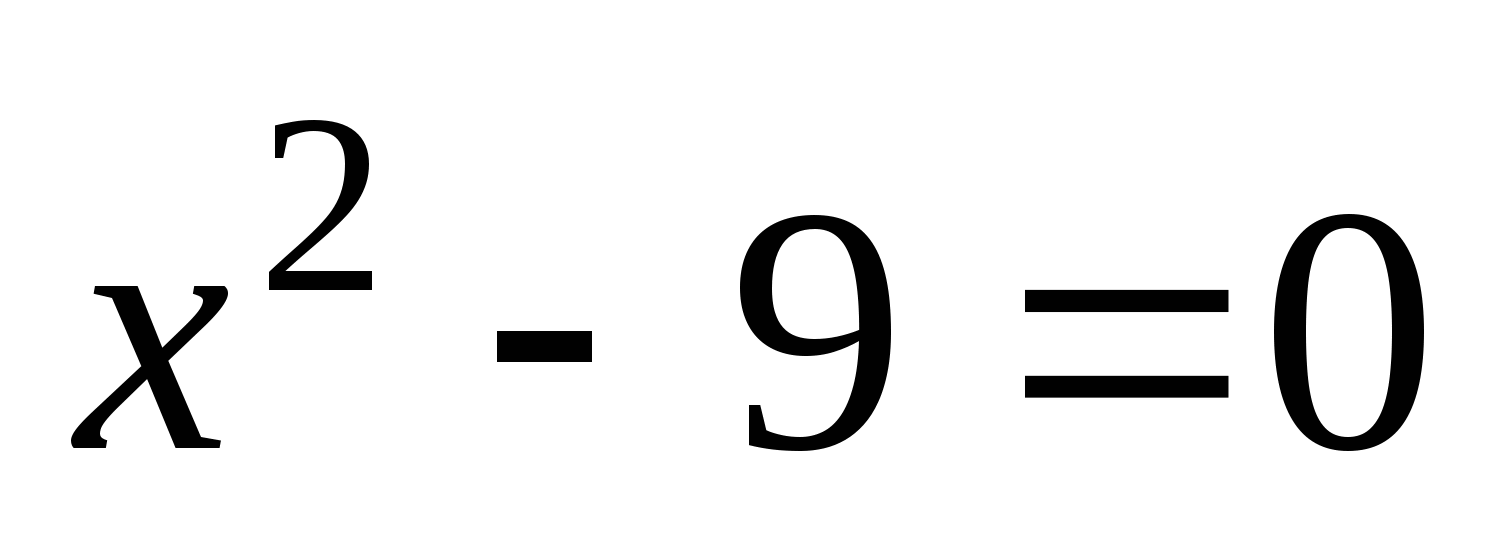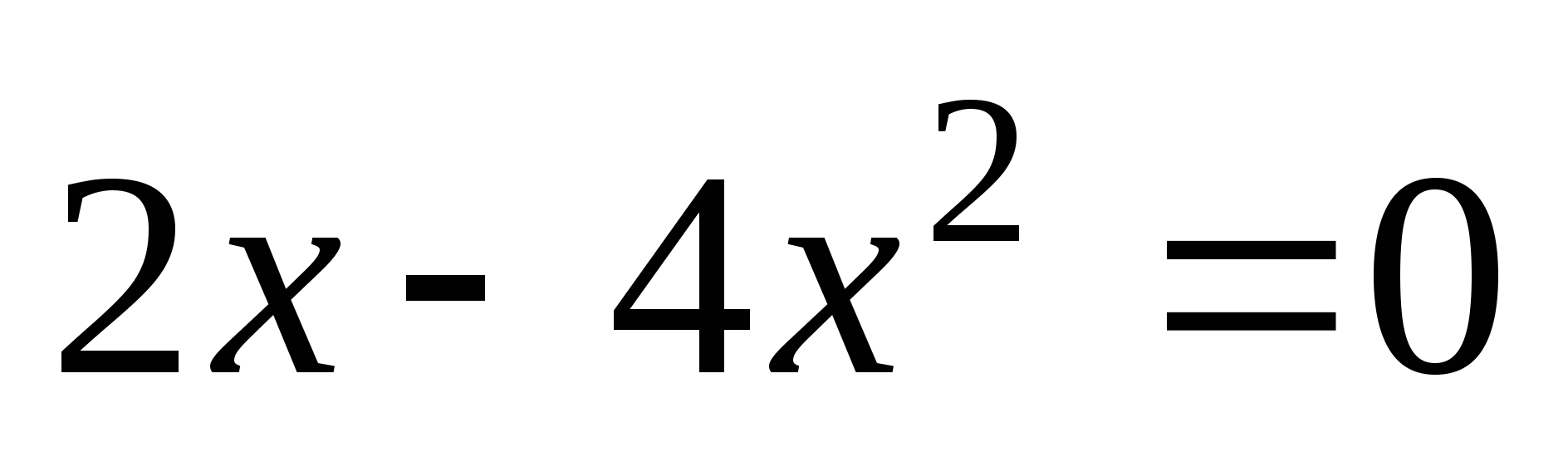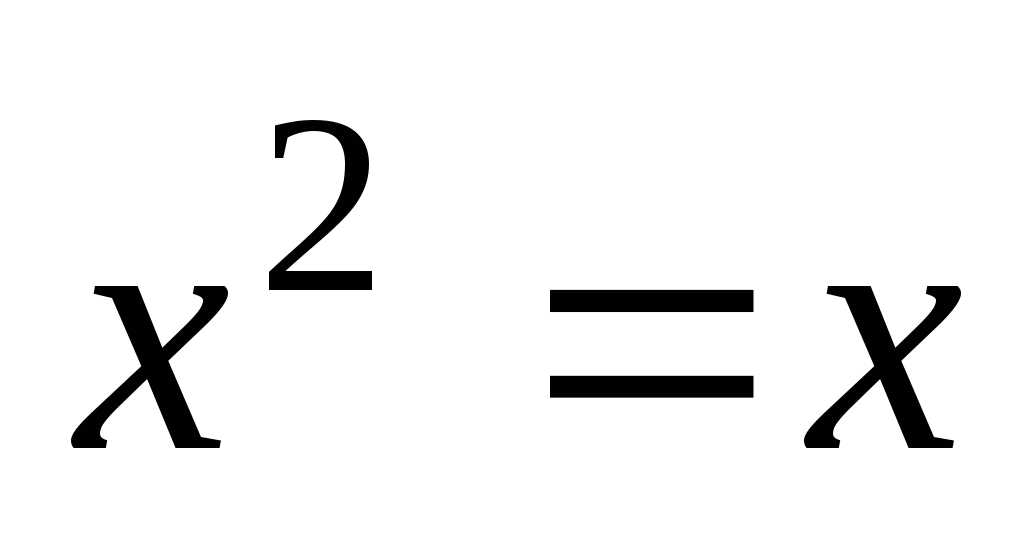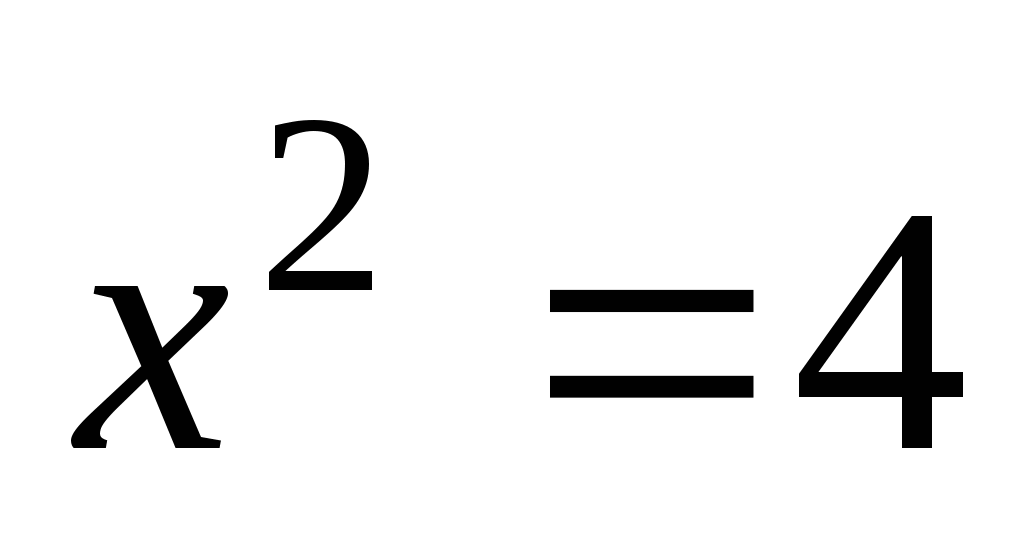
6. Повторить алгоритм решения неполного квадратного уравнения с помощью разложения на множители.

III. Изучение новой темы

Цель - разработать алгоритм графического решения уравнений

1. Проблема: Как решить уравнения 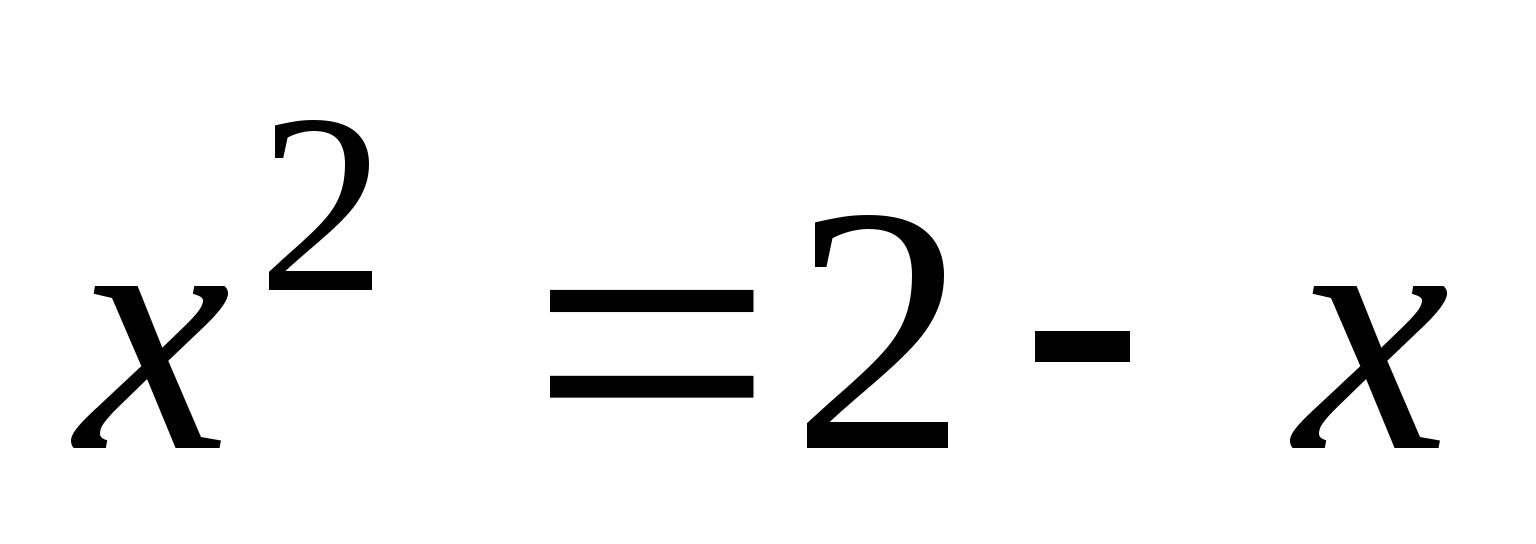и ?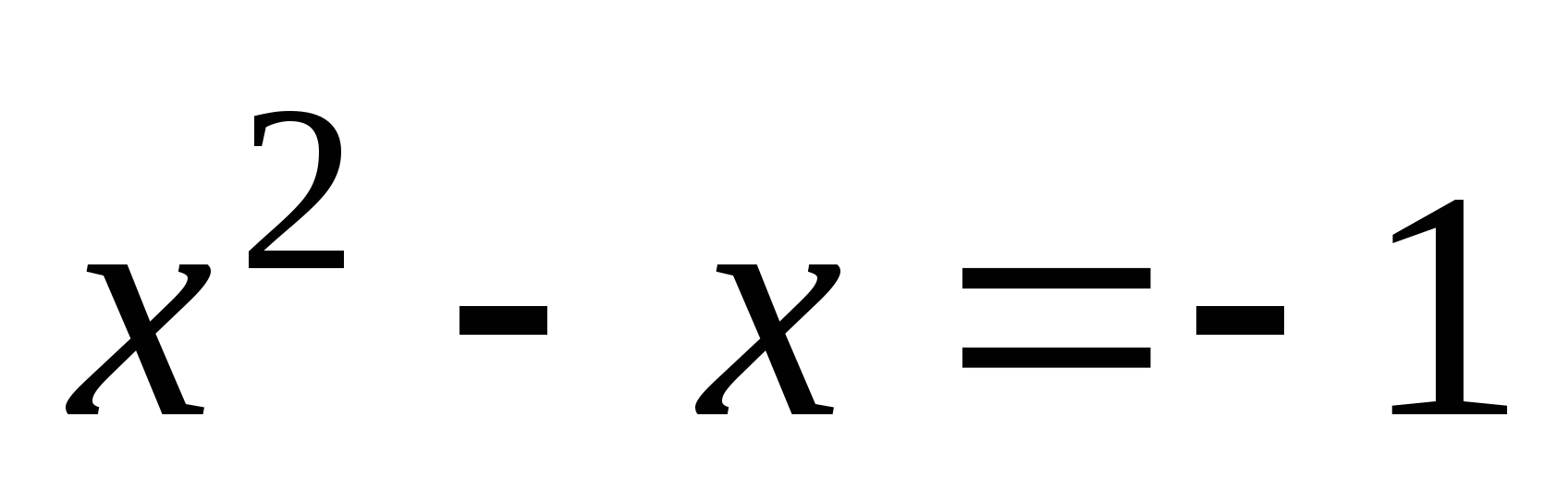

Очевидно, существует способ, позволяющий свести данные уравнения к уже известным нам фактам.

Посмотрим на левую часть уравнения 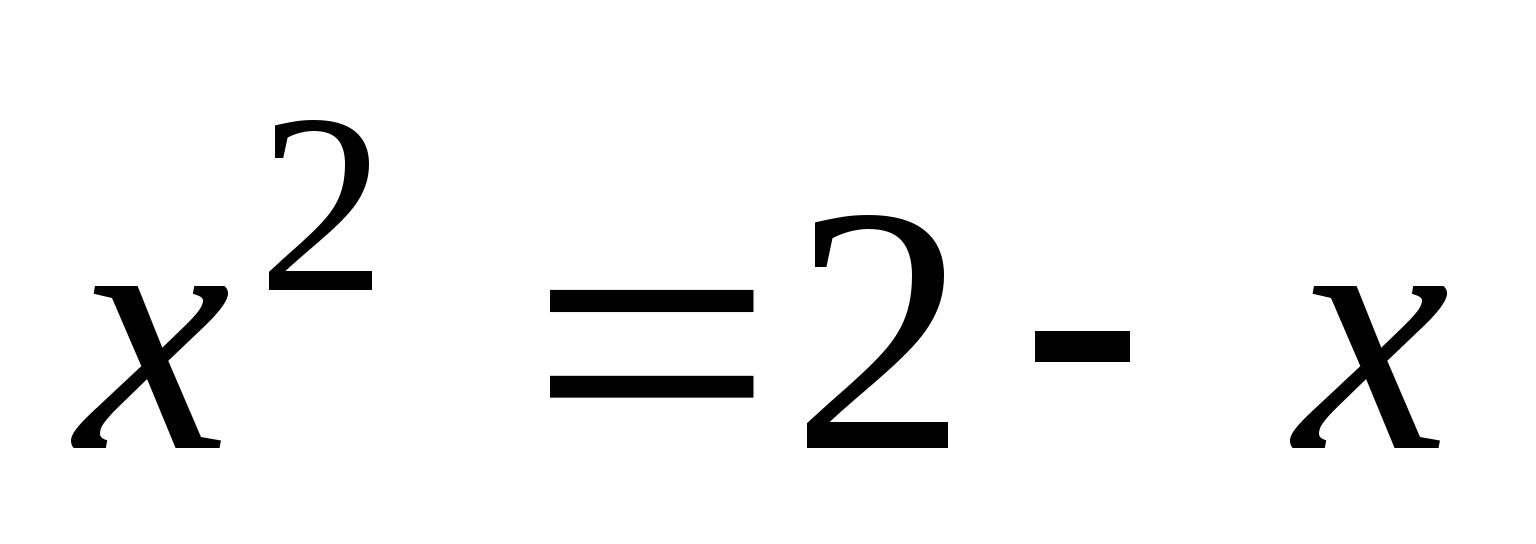. Это часть функции .

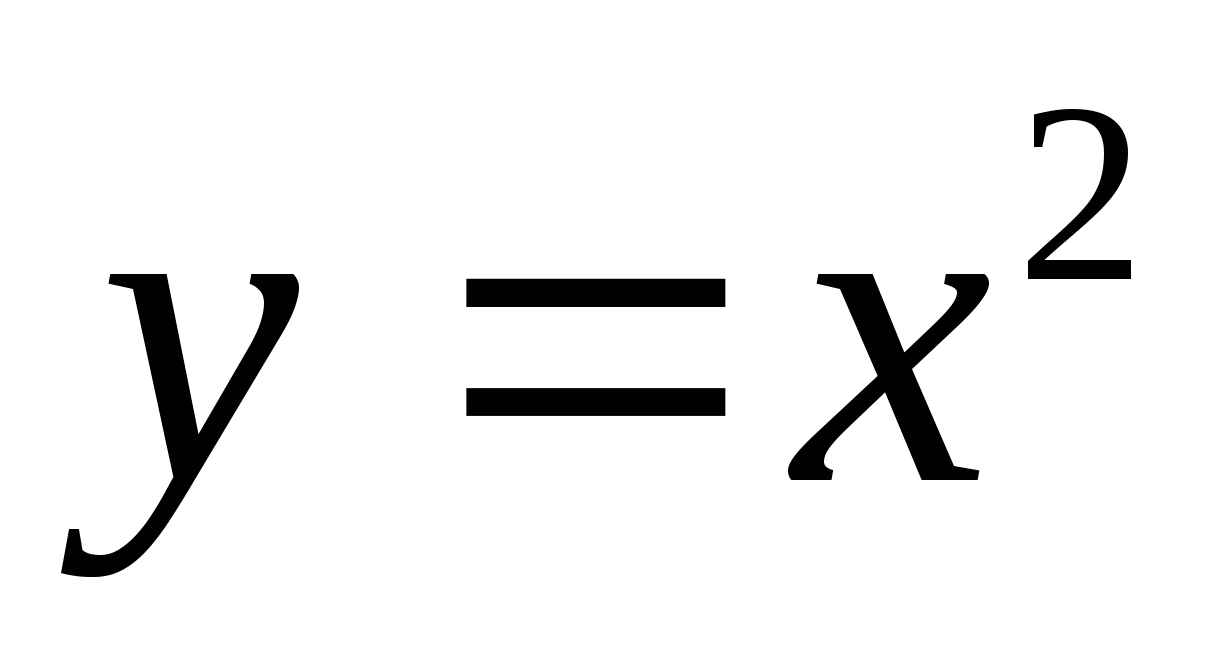Посмотрим на правую часть уравнения 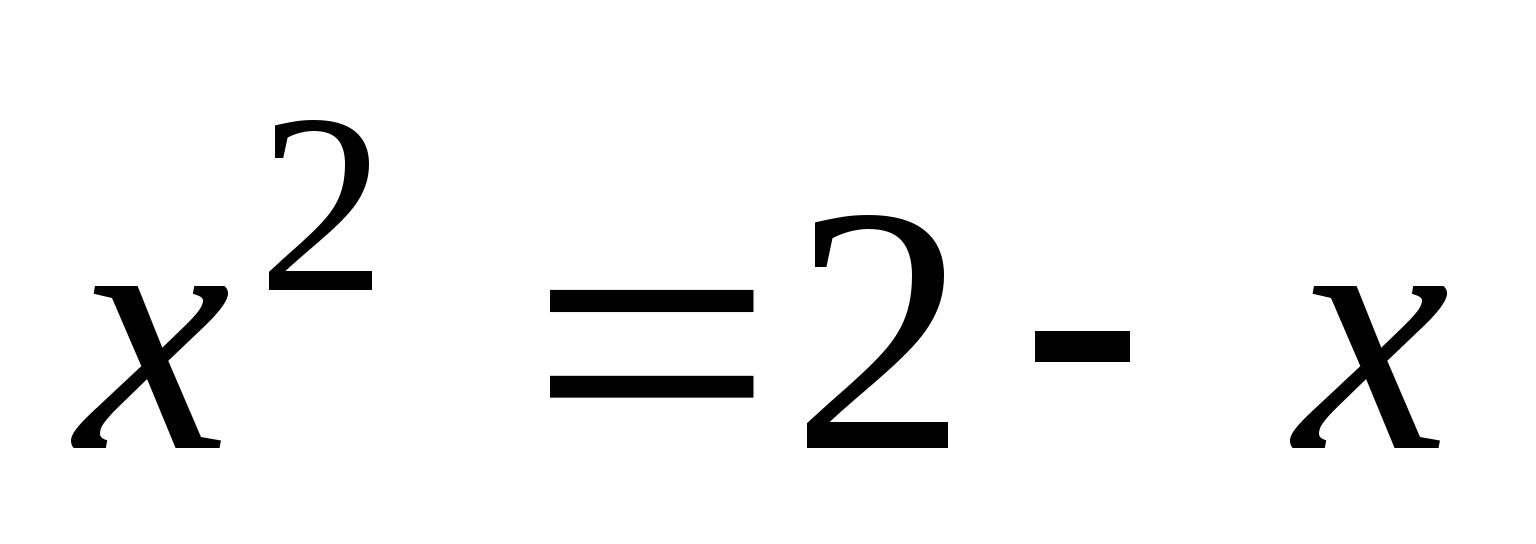. Это часть функции .

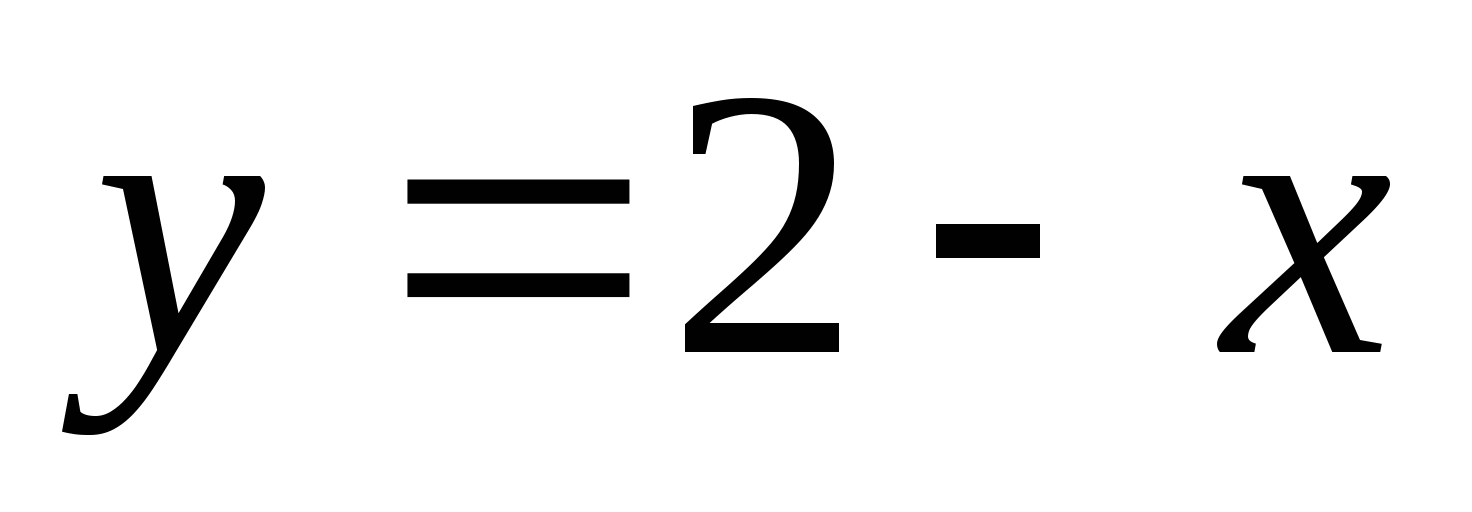Можем ли мы использовать это при решении уравнения? Каким образом?

Строим в одной системе координат графики функций (комментарии в ходе построения) 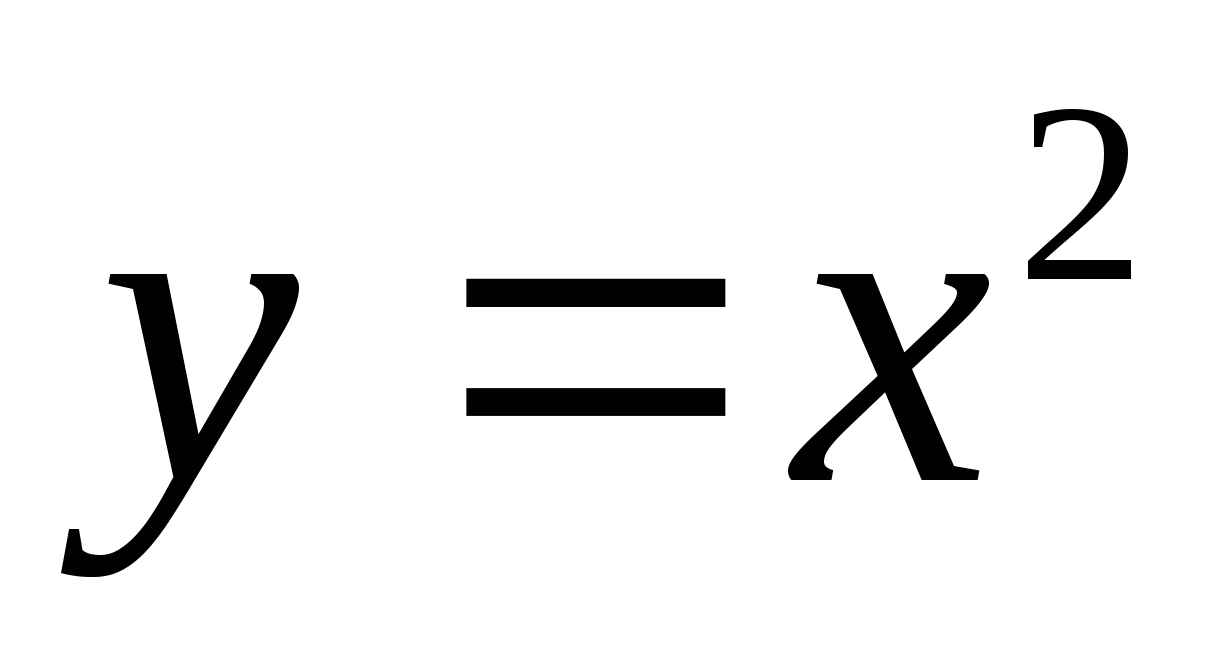и .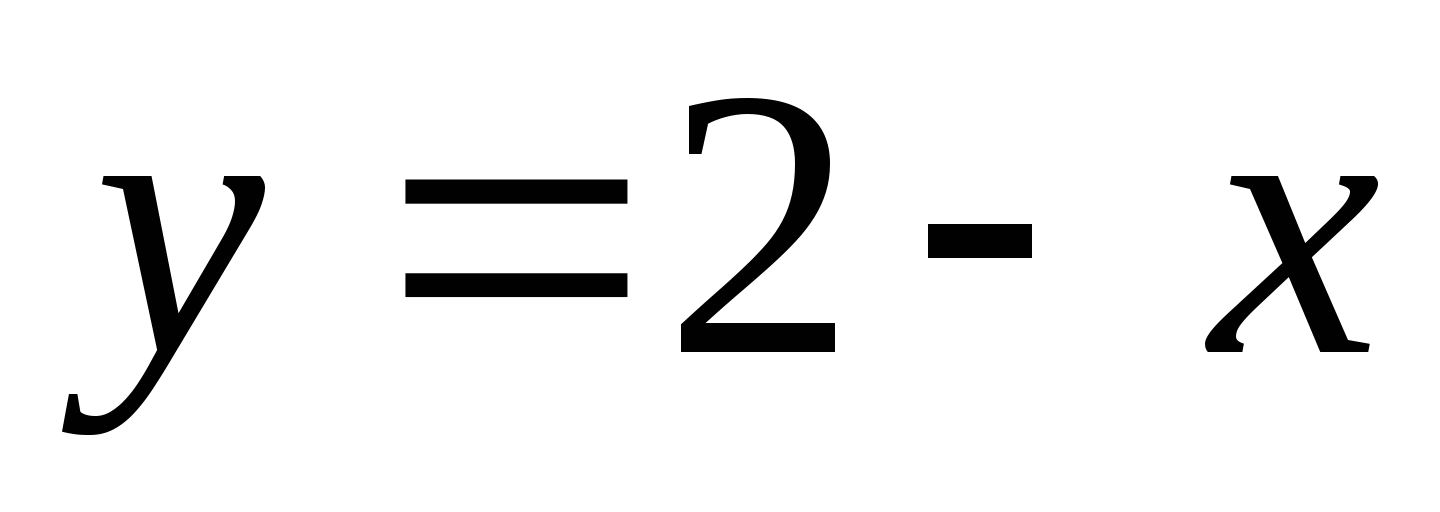

Как определить корни уравнения?

Решим второе уравн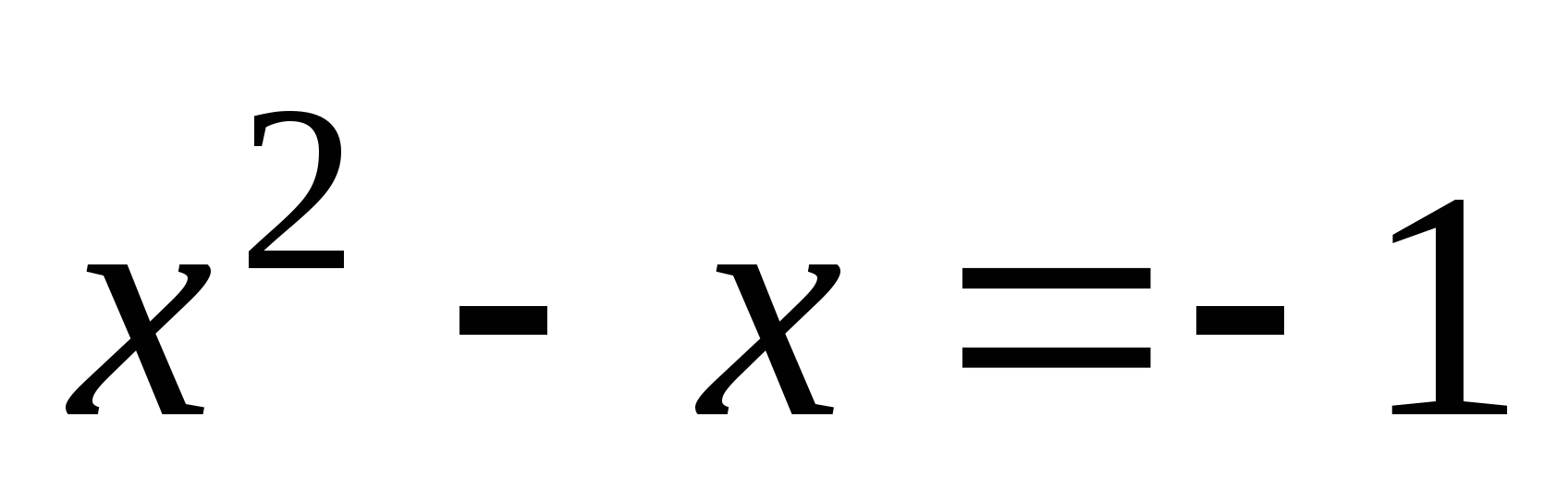ение . Чем оно отличается от первого? Можно ли записать его в таком же виде, как первое уравнение? 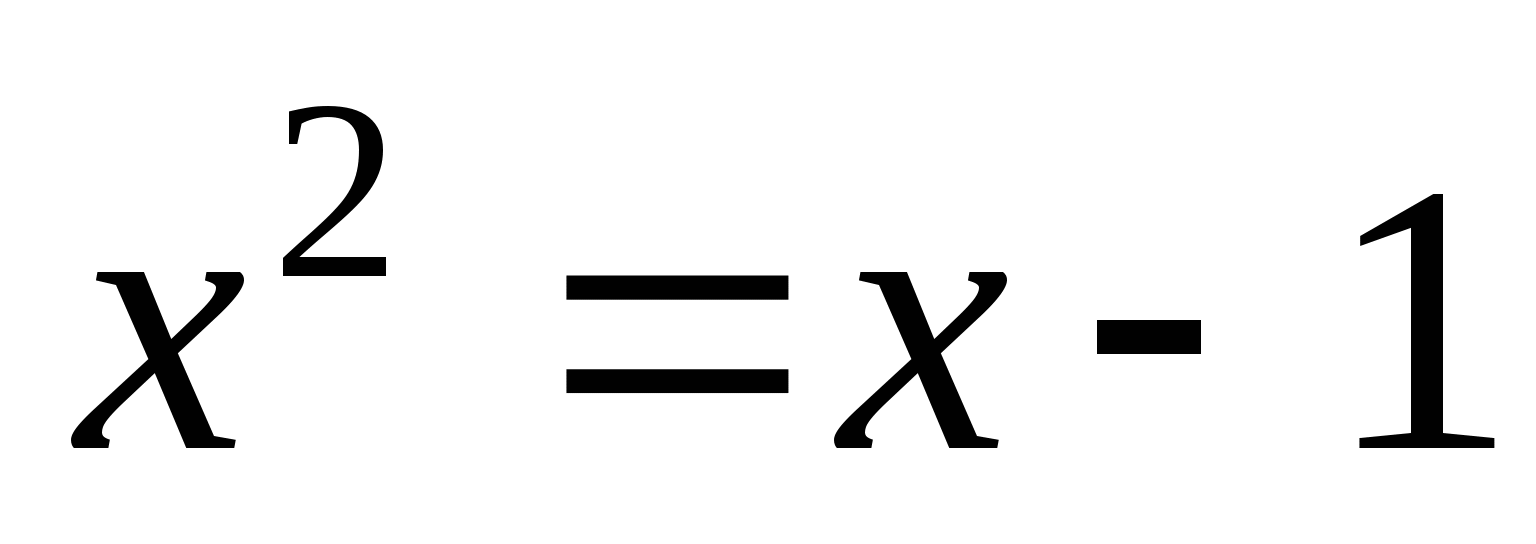. Строим графики.

Что можно сказать о корнях этого уравнения?

2. Подведём итог. Для решения уравнения с помощью графиков нужно:

1. Привести уравнение к виду .

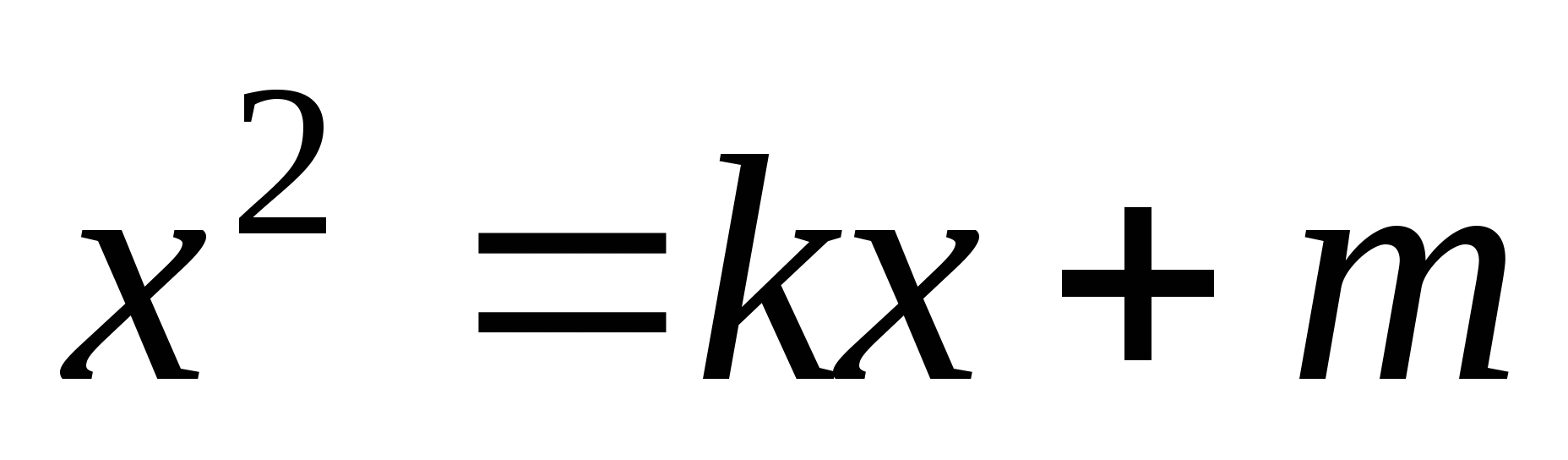2. Ввести 2 функци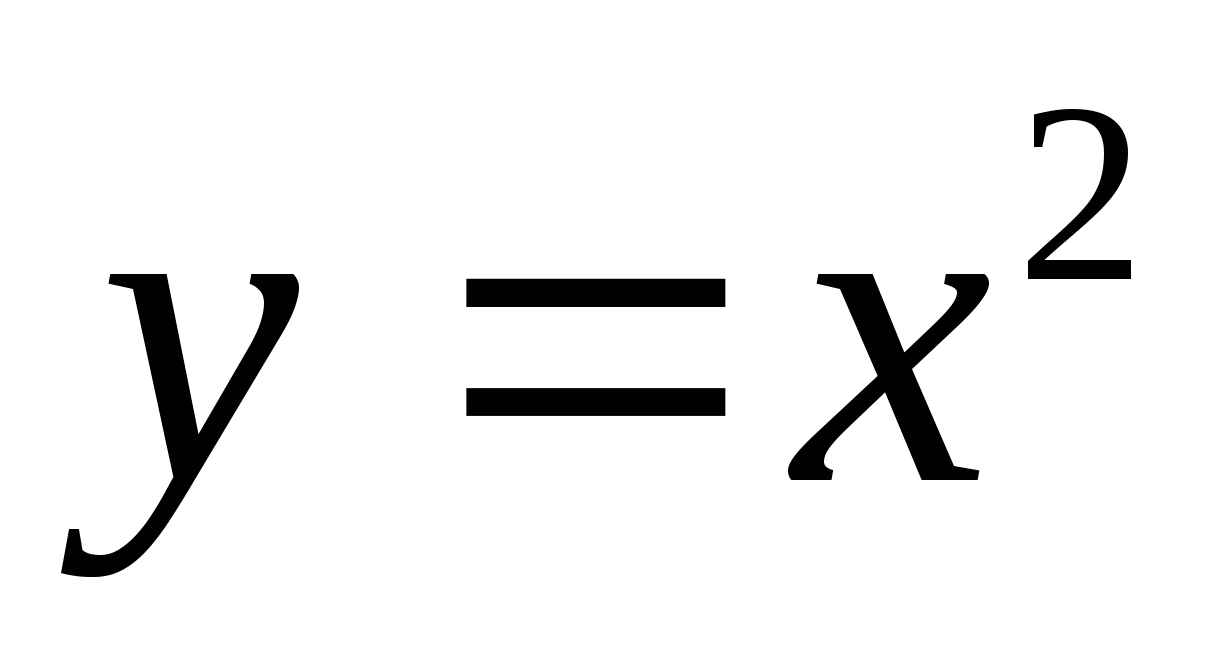и и .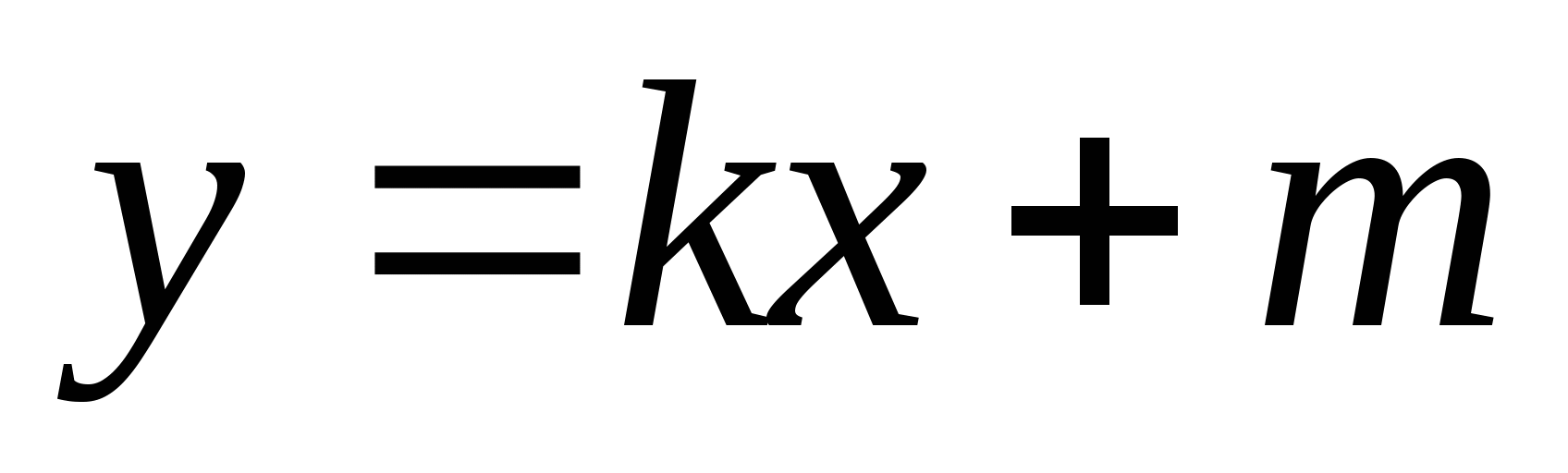

3. Построить в одной системе координат графики этих функций.

4. Проверить, пересекаются ли графики функций:

А) если графики пересекаются, то записать абсциссы точек пересечения - это корни уравнения;

Б) если графики не пересекаются, то уравнение корней не имеет.

IV. Решение задач

Цель -первичное закрепление алгоритма графического решения уравнений

Решение уравнений по готовым чертежам

Решение задач из задачника (№№ 996(а, г), 997(а, в), 1002)

IV. Самостоятельная работа

Цель - первичный анализ усвоения алгоритма графического решения уравнений

Решить уравнения:

1 вариант

1)

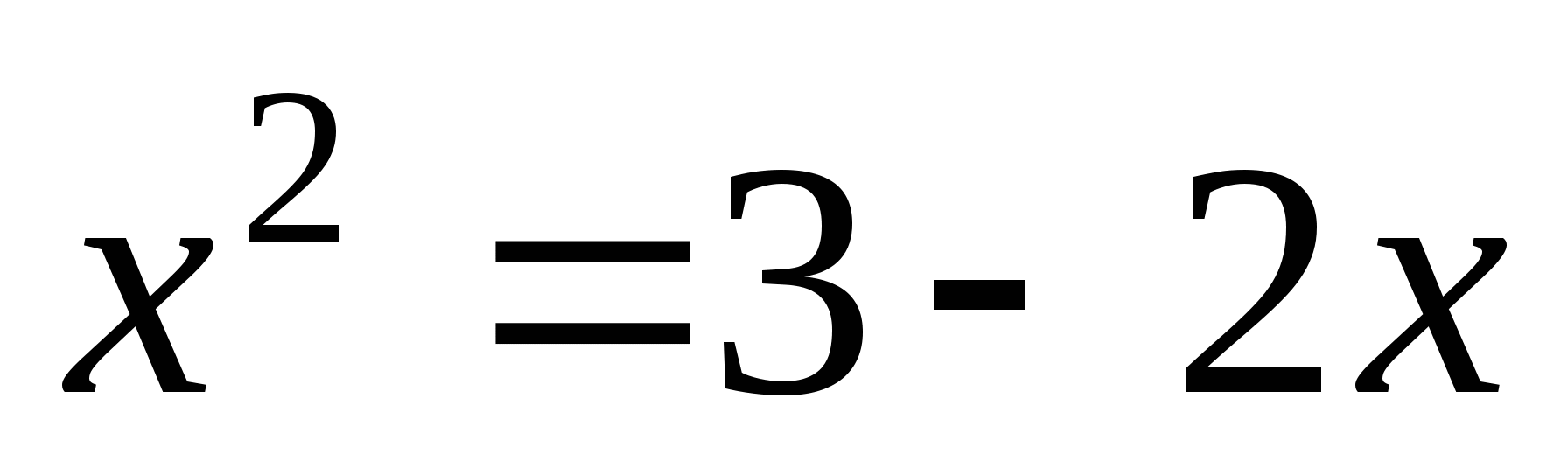
2)

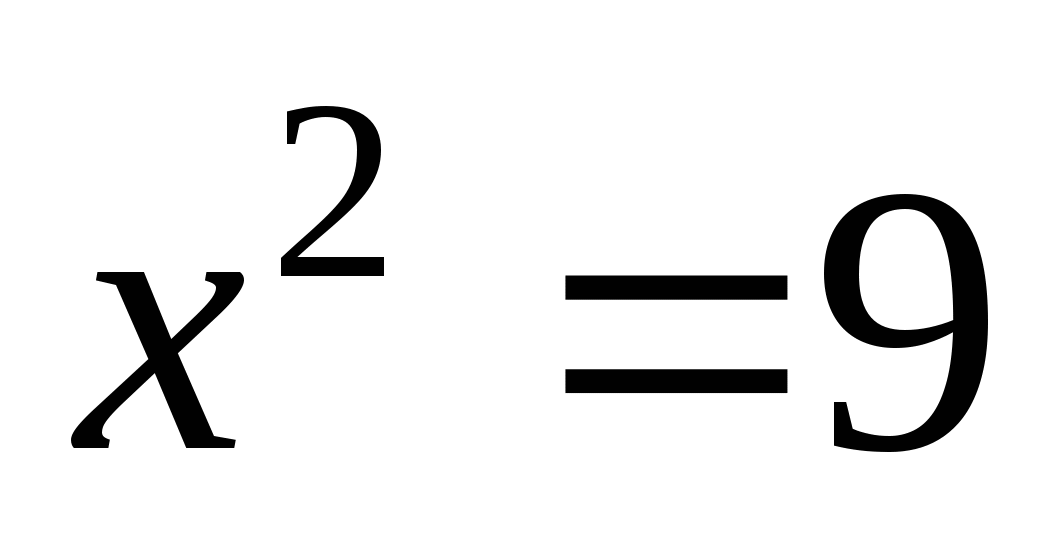
2 вариант

1)

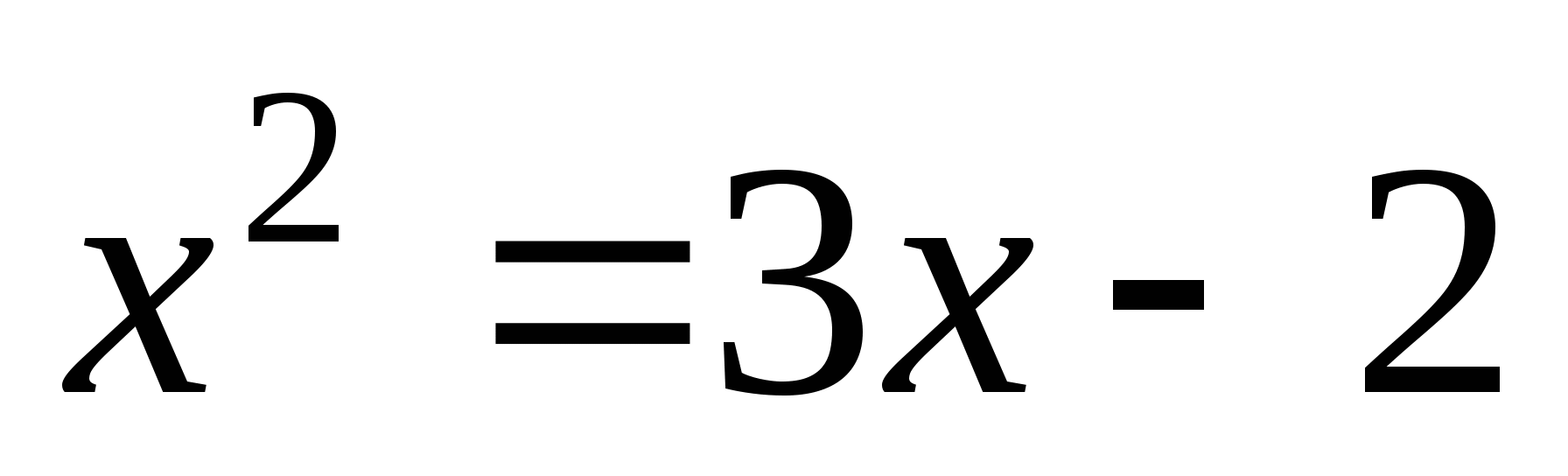
2)

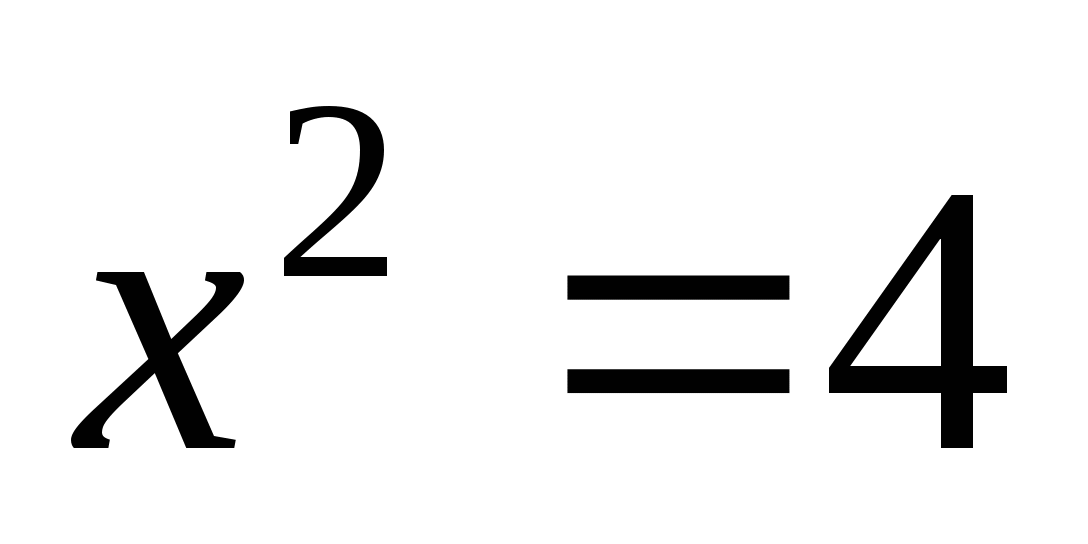
Взаимопроверка по готовым ответам.

V. Подведение итогов урока, рефлексия.

Цель - проанализировать успехи и неудачи работы на уроке

VI. Домашнее задание:

1. § 33, выучить алгоритм графического решения уравнений

2. Решить задачи №№ 35.6(б, г), 35.7(а, б), 35.10(а, б), 35.13(а)

3. По желанию: подобрать и решить три уравнения различной сложности, которые можно решить с помощью графиков.