урок по АНА в 11 классе 'Наибольшее и наименьшее значение функции'

Михайлова Ирина Владимировна, учитель математики,

МОУ «СОШ №4», г. Ялуторовск

Предмет: алгебра и начала анализа, 11 класс.

Тема урока: «Наибольшее и наименьшее значение функции».

Цели урока: 1) формирование умений и навыков нахождения наибольшего (наименьшего) значения функции на интервале, на отрезке с помощью производной и применение их при решении задач;

2) акцентирование внимания учащихся на задачах данной темы, выносимых на экзамен по математике;

3) обеспечение коридора индивидуального развития для учащихся класса по теме.

Тип урока: закрепление материала по данной теме.

Форма урока: семинар-практикум.

Форма организации деятельности учащихся на уроке: индивидуальная (компьютер), дифференцированно-групповая.

Оборудование: тетради, ручки, карандаши; учебник Ш.А. Алимова, Ю.М. Колягина и др.; ПК, проектор, экран (или интерактивная доска), доска, мел.

План урока.

№ п/п

Этап урока

Цель этапа

Время проведения этапа урока

1

Начало урока

Сообщение темы урока, постановка целей урока.

1-2 минуты

2

Устная работа. Проверка домашнего задания

Повторить формулы производных элементарных функций, план нахождения наибольшего или наименьшего значения функции с помощью производной.

4-5 минут

3

Фронтальное решение у доски задачи №944(1) с подробным следованием плану решения.

Формирование умений и навыков у учащихся применять производную для нахождение наибольшего (наименьшего) значений функции.

6-8 минут

4

Работа в микрогруппах.

Выявление пробелов в знаниях учащихся, создание условий для индивидуального развития ученика на уроке.

15-22 минут

5

Подведение итогов работы.

Отследить успешность работы учащихся при самостоятельном решении задач по теме, выяснить характер затруднений, их причины, указать коллективно пути решения.

5-6 минут

6

Домашнее задание.

Познакомить учащихся с заданием на дом. Дать необходимые пояснения.

1-2 минуты

Михайлова И.В.

Ход урока.

1. Начало урока.

Приветствие класса. Вопросы: «Какую тему начали рассматривать на прошлом уроке? Чему необходимо нам научиться при изучении данной темы?». Провести корректировку целеполагания учащихся, если это необходимо. Обратить внимание на важное положение данной темы в содержании материала, выносимого на экзамен по математике.

2. Устная работа. Проверка домашнего задания.

1) Двое учащихся на доске записывают решение №№937(2), 938(2), 939(2) домашнего задания.

2) Обратить внимание учащихся на экран. (Приложение 1). Предложить выполнить устно задания, представленные на слайдах.

3) Фронтально проверить выполнение домашнего задания. Повторить порядок нахождения наибольшего/наименьшего значений функции с помощью производной (см.[1], стр.273).

3. Коллективное решение задачи №944(1) с подробным следованием плану решения с приглашением одного ученика к доске.

Решение: 1. y=ln x-x. Находим значения функции на концах отрезка [;3]:

y()=ln- <0;

y(3)=ln3-3<0.

2. Находим производную функции: y'= (ln x-x)'=-1.

3. Находим критические точки функции: -1=0; =0;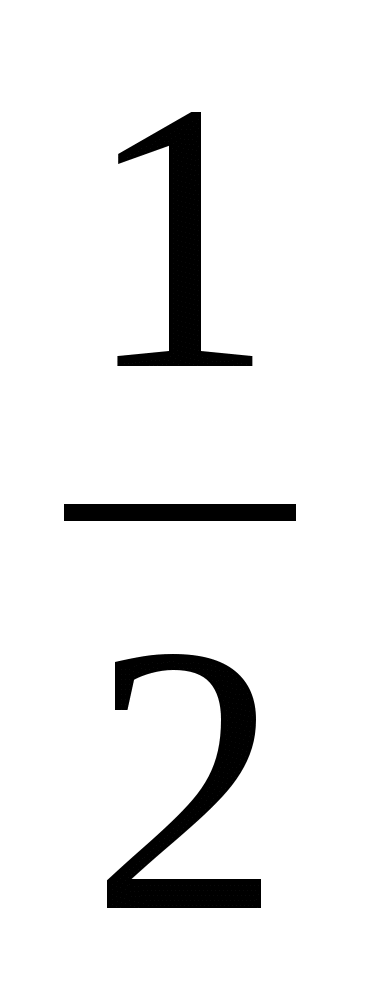

4. Находим промежутки монотонности функции (рис.1):

-

_+

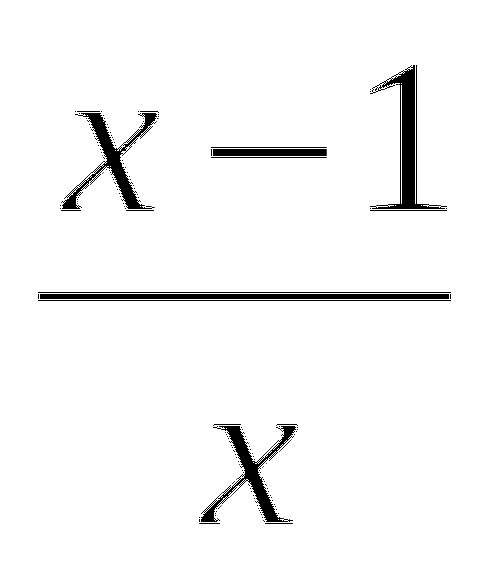
0

1

рис. 1.

5. В точке х=1 функция имеет наименьшее значение: y = ln1-1=-1/

Проведя оценку результатов, получаем: наименьшее значение функции у= ln3-3, у= -1.

Ответ: у= ln 3-3, у= -1.

4. Работа в микрогруппах.

Для дальнейшей работы учащимся предлагается практикум, составленный в программе EXCEL, состоящий из 5 заданий разного уровня трудности, но не превышающий в общем по сложности базового уровня (Приложение 2).

В ходе выполнения работы учащиеся могут, по желанию, объединяться в пары, что позволяет им достигать не только самообучения, но и взаимообучения друг друга по данной теме урока, способствует осознанию изучаемого материала. Индивидуальный темп работы позволяет избежать напряжённости на занятии.

5. Подведение итогов работы. Выставление оценок за работу на уроке.

6. Домашнее задание: §52, карточки с заданиями, составленные по тематическим сборникам.

Содержание домашнего задания:

1.Функция y=f(x) определена на промежутке (a;b). На рисунке 2. изображён график её производной. Найдите число точек максимума функции y=f(x) на промежутке (a;b). ([2], с.13)

2. Найдите наименьшее значение функции y = x(x+2)на отрезке [-1;1].

([3], с.60)

3. Найдите наибольшее значение функции y = 3cos x + 1 на отрезке

[-2005;2005]. ([3], с.64)

4. Найдите наименьшее значение функции f (x) = . ([3], с.61)

Литература:

1. Ш.А. Алимов, Ю.М. Колягин и др./Алгебра и начала анализа: учеб. для 10-11 кл. общеобразоват. учреждений/ М.: Просвещение, 2007.-384 с.

2. Единый государственный экзамен: математика: контрол. измерит. материалы:2005-2006/под общ. Ред. Л.О. Денищевой; М-во образования и науки Рос. Федерации, Федерал. Служба по надзору в сфере образования и науки, ФИПИ. - М.: Просвещение, 2006. - 96 с.

3. В.В. Кочагин, М.Н. Кочагина /ЕГЭ-2008. Математика. Тематические тренировочные задания - М.: Эксмо, 2008. - 136 с.