Практическая работа по теме Комплексные числа

Предмет: «Элементы высшей математики»

Практическая работа

Тема: Операции над комплексными числами.

Цели занятия:

• сформировать навыки изображения и записи комплексного числа в алгебраической и тригонометрической форме;

• сформировать навыки проведения простых действий (сложений, вычитания, умножения и деления) с комплексными числами.

Теоретические сведения к практической работе

Комплексное число - это выражение вида

, (1.1)

где x, y - вещественные числа, а - мнимая единица.

x - вещественная (действительная) часть комплексного числа (используется обозначение );

y - мнимая часть ().

Выражение (1.1) называют алгебраической формой записи комплексного числа.

Числом, сопряженным к , называют число вида . Используя формулу разности квадратов, получаем, что . Можно доказать, что корнями квадратного уравнения с отрицательным дискриминантом являются два сопряженных комплексных числа.

Пример 1. Решить уравнение .

Решение. Дискриминант данного уравнения: меньше нуля, но теперь мы можем воспользоваться мнимой единицей:

, т.е. ; .

Арифметические действия над комплексными числами

1) Сложение (вычитание) комплексных чисел:

;

2) Умножение комплексных чисел:

(осуществляется с учетом того, что );

3) Деление комплексных чисел:

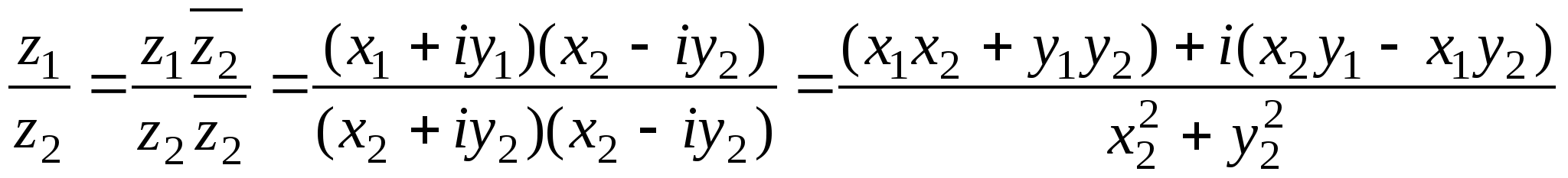(эта операция возможна только в случае, когда ).

Пример 2. Вычислить и указать вещественную и мнимую части полученного комплексного числа.

Решение. Действуя в соответствии с правилами получаем:

;

поэтому , .

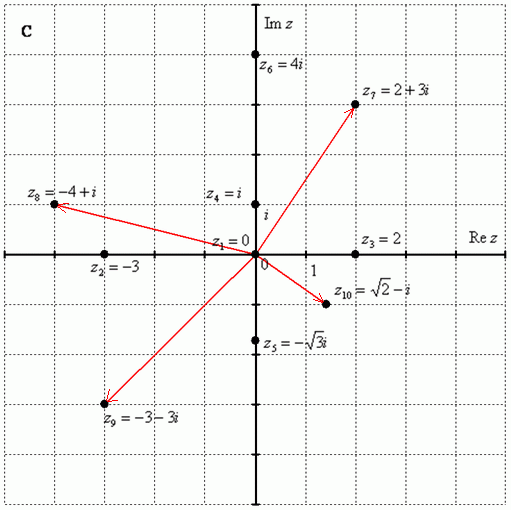
Тригонометрическая форма комплексного числа. Каждому комплексному числу вида (1.1) можно поставить в соответствие точку M(x;y) на декартовой плоскости (при этом на оси OX располагаются вещественные числа , а на оси OY - чисто мнимые числа ). Вектор OM считают изображением комплексного числа.

Модулем комплексного числа назовем длину отрезка (или расстояние от начала координат до точки M), т.е. . Аргументом комплексного числа () назовем угол, который вектор образует с положительным направлением оси OX. Главное значение аргумента, которое, как правило, используется при осуществлении действий с комплексными числами, удовлетворяет условию . При этом выражение вида

(1.2)

называется тригонометрической формой записи комплексного числа.

Преобразуем (1.1)

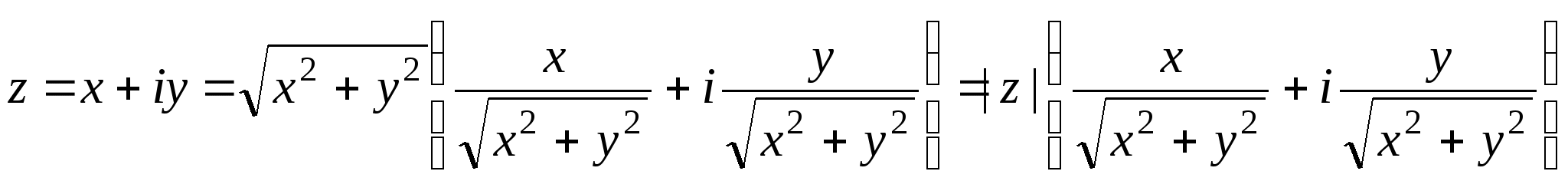
и, сравнивая с (1.2), получаем, что аргумент z можно найти, решив систему

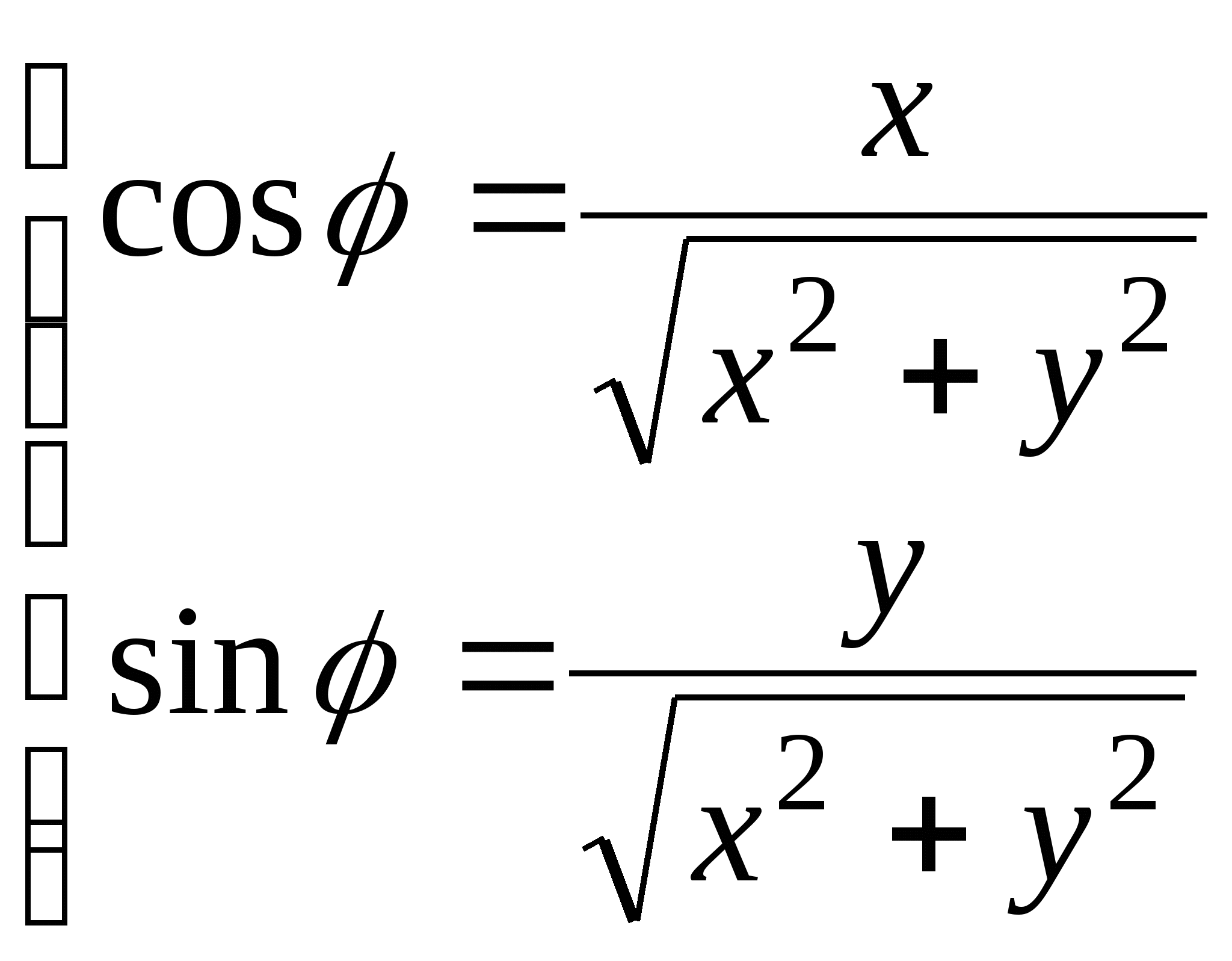или 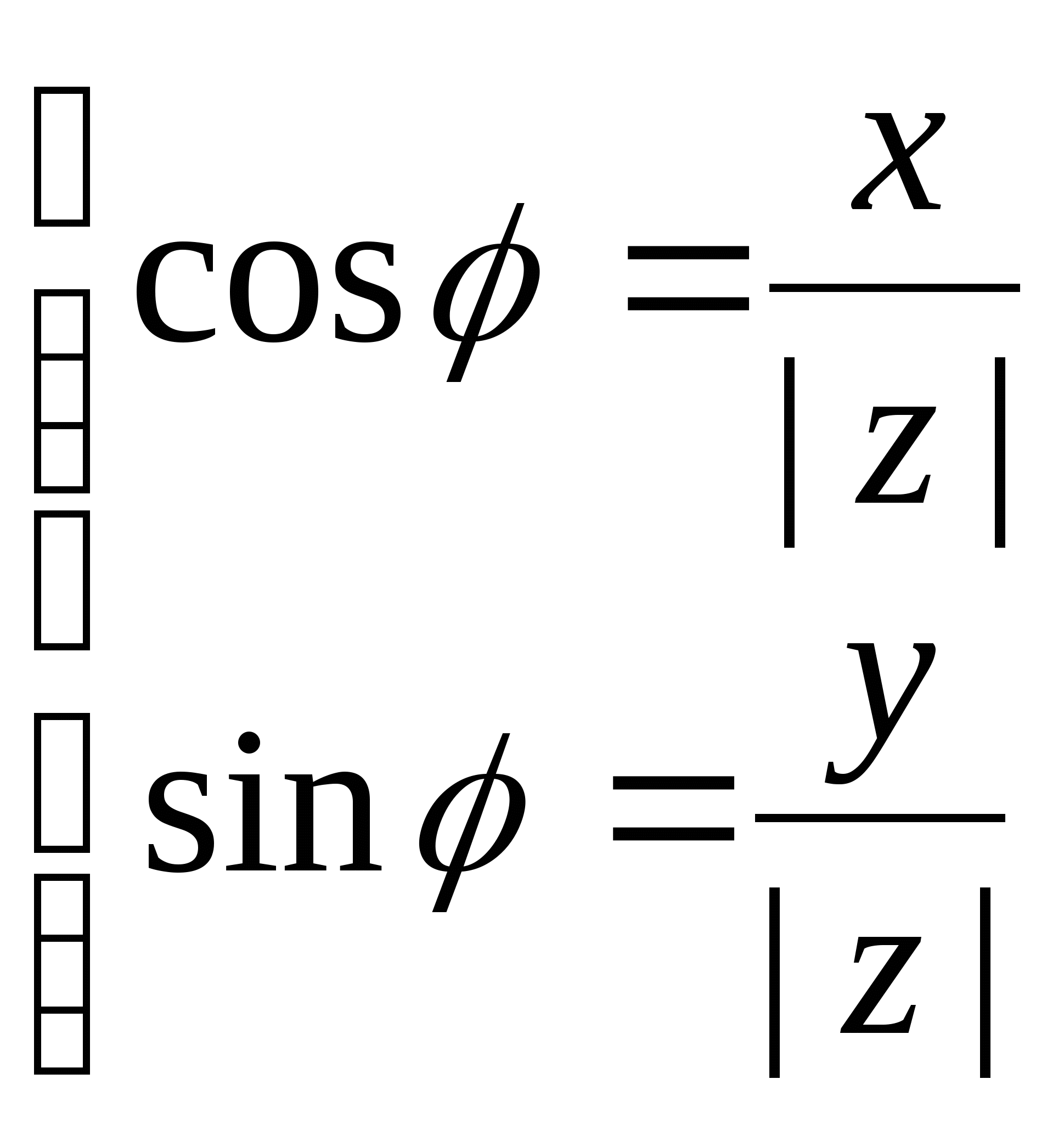(1.3.)

Пример 3. Записать комплексное число в тригонометрической форме _{, указать модуль и аргумент комплексного числа.}

Решение. По определению . Для определения аргумента воспользуемся формулой: 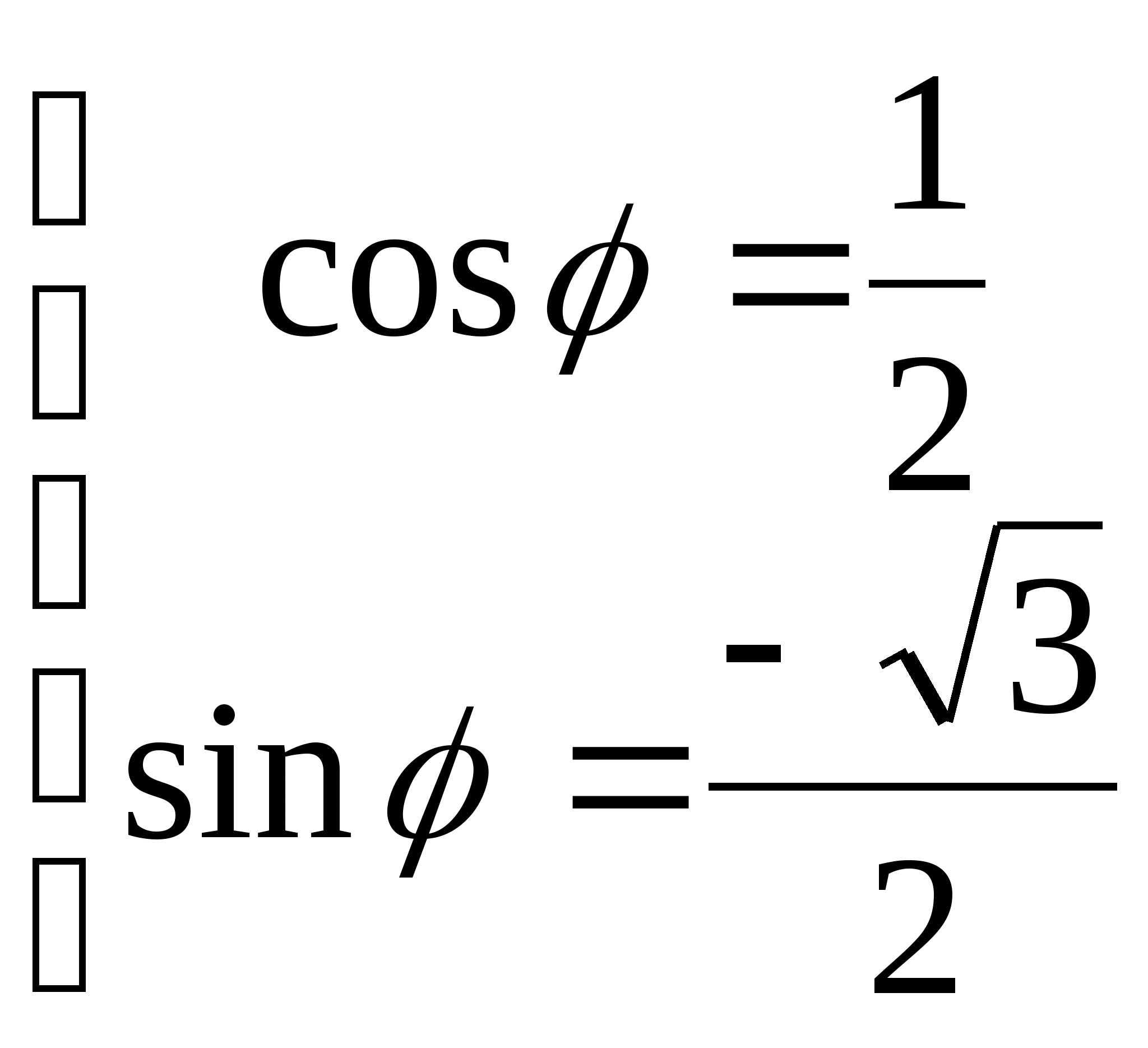. Получаем, что . Тригонометрическая форма заданного комплексного числа имеет вид: .

Возведение в степень и извлечение корней. Если комплексное число задано тригонометрической формой , то справедлива формула Муавра

. (1.4)

Для извлечения корня n-й степени (n - целое число, большее 1) из комплексного числа, заданного в тригонометрической форме, применяется формула, дающая n значений этого корня:

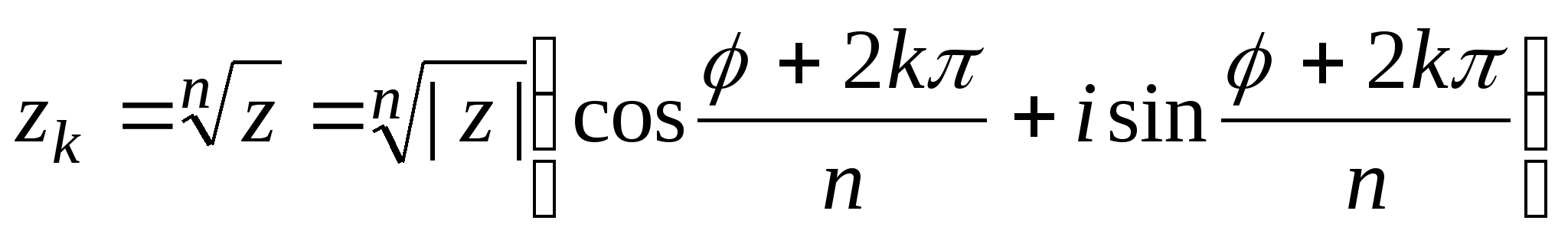, k=0,1,…,n-1. (1.5)

Пример 4. Вычислить: a) ; b) .

Решение. В задании a), чтобы воспользоваться формулой Муавра, необходимо представить комплексное число в тригонометрической форме. Имеем: ; и , т.е. (так как соответствующая точка лежит во второй четверти). Следовательно, и 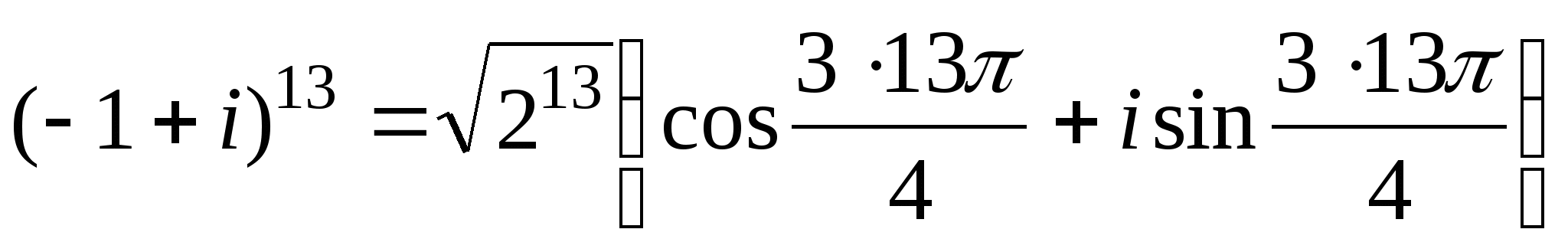(в силу (1.4)). Учитывая что и используя свойства тригонометрических функций, получаем:

.

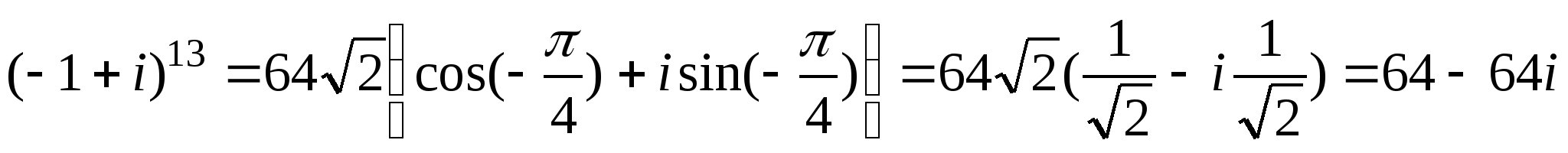В задании b) тригонометрическая форма заданного числа имеет вид (|z|=1), поэтому в силу (1.5)

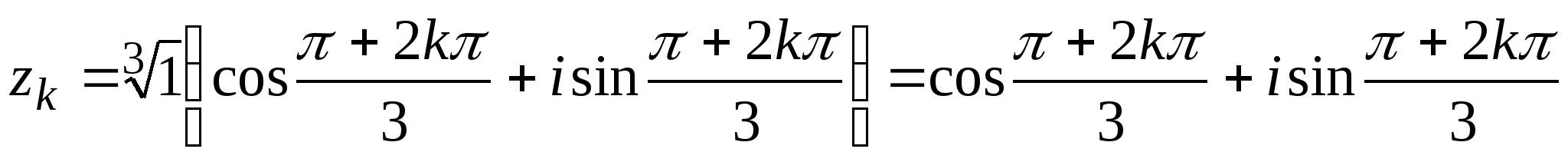, k=0,1,2.

Выписываем три искомых корня:

;

;

.

Практическая часть:

1 часть занятия: совместное решение задач (работа у доски).

Задание 1. Вычислить, выписать вещественную и мнимую части полученных комплексных чисел.

1) 2) 3)

4) 5) 6)

7)

Задание 2. Запишите предложенные комплексные числа в тригонометрической форме: 1) ; 2) ; 3) ; 4) _{5) 6) 7)} .

Задание 3. Найти все корни уравнений:

1) ; 2) ; 4) ; 5) ; 6) 7)

Примечание:

2 часть занятия: Самостоятельная работа.

Представьте комплексное число в тригонометрической форме:

а)

б)

а)

б)

а)

б)

Рекомендуемая литература:

1. Валуцэ И.И., Дилигул Г.Д. Математика для техникумов. - М.: Наука, 1990.

2. Подольский В.А., Суходский А.М., Мироненко Е.С. Сборник задач по математике. - М.; Высшая школа, 1998.

ГАПОУ Учалинский колледж горной промышленности Преподаватель: Гайнутдинова Д.Р.