- Учителю
- « Решение уравнений и неравенств с параметрами» Программа дополнительного образования для учащихся 9 классов
« Решение уравнений и неравенств с параметрами» Программа дополнительного образования для учащихся 9 классов
Муниципальное образовательное учреждение средняя обрщеобразовательная школа №44
с углубленным изучением отдельных предметов
Центрального района г. Волгограда
Утверждена
Методическим советом
Протокол №____от «____»________2013г.
Директор МОУ СОШ №44
__________ Комиссарова И.В.
« Решение уравнений и неравенств с параметрами»
Программа дополнительного образования
для учащихся 9 классов
Составитель:
Литвинчук Ипмев Анатольевна
учитель математики
Волгоград 2013
Пояснительная записка
Цель программы:
Социальная цель - расширяет представления учащихся о математике как универсальном языке науки, средстве моделирования явлений и процессов, знакомит с универсальными методами решения алгебраических задач, способствует развитию логического мышления и математической интуиции; помогает осознавать степень своего интереса к предмету и оценивать возможности овладения им с точки зрения дальнейшей перспективы; формировывает качества мышления, характерные для математической деятельности и необходимые человеку для жизни в современном обществе.
Педагогическая цель - исследование и решение задач с параметрами на основе алгоритма решения, применять тот или иной способ при решении заданий с параметрами.
Направленность программы - учебно-познавательная.
Структура программы состоит из двух образовательных блоков: теория и практика.
Наполняемость обучающихся в каждой группе составляет до 12 человек. Данная программа по теме «Нестандартные методические приемы решения различных неравенств» для учащихся 9 классов рассчитана на 26 часов в объеме один час в неделю. Продолжительность занятий 40 минут.
Актуальность:
Актуальность данной программы состоит в том, что задания с параметрами обладают большим развивающим потенциалом. Они способствуют повышению уровня логического мышления, а так же формируют навыки исследовательской деятельности.
Педагогическая целесообразность: позволяет формировать умения по решению задач с параметрами, сводящихся к исследованию линейных и квадратных уравнений и неравенств, поддерживает изучение основного курса математики, способствует лучшему усвоению базового курса математики и направлен на расширение знаний учащихся, повышение уровня математической подготовки через решение большого количества неравенств нестандартными приемами; формирует практические навыки решения математических задач, развивает алгоритмическую культуру и математические знания и умения, необходимые в повседневной жизни.
Задачи:
-
изучение дополнительного материала;
-
овладение системой математических знаний и умений;
-
способность различать факт, мнение, доказательство, гипотезу, аксиому;
-
приобретение исследовательских компетенций - поиск функциональных связей и отношений между частями целого. Разделение процессов на этапы, звенья;
-
воспитание культуры личности, понимание значимости математики научно технического прогресса;
-
развитие качеств личности, необходимых человеку в современном обществе.
Формы занятий:
-
индивидуальная;
-
парная;
-
групповая;
-
коллективная.
В основе формирования практических навыков решения математических задач лежат два главных вида деятельности учащихся: это обобщение и систематизация теоретических знаний, полученных ранее и отработка умений и навыков на практике.
Методами диагностики являются:
-
фронтальный опрос;
-
проверка задач самостоятельного решения.
Методы обучения:
-
лекция;
-
рассказ;
-
объяснение;
-
решение задач.
Учебный план
п/п
Наименование разделов плана
Общее количество часов
В том числе
теория
практика
Задачи с параметрами. Основные сведения
1
0,5
0,5
Линейные уравнения с параметрами
4
2
2
Решение задач на основе теоремы о существовании корней квадратного трехчлена
5
2
3
Исследование и решение систем линейных уравнений
4
1
3
Линейные неравенства с параметрами
2
1
1
Исследование и решение неравенств второй степени с параметрами
3
1
2
Фазовая плоскость
3
1
2
Решение задач по данным темам
4
1
3
Итого
26
9,5
16,5
Учебно-тематический план
п/п
Наименование разделов плана
Общее количество часов
В том числе
теория
практика
Задачи с параметрами. Основные сведения
1
0,5
0,5
1.1
Что такое параметр? Что означает решить задачу с параметром?
0,5
0,5
Линейные уравнения с параметрами
4
1,5
2,5
2.1
Первые представления о решении уравнений с параметром
0,5
0,5
2.2
Простейшие линейные уравнения с параметром
0,5
0,5
2.3
Решение линейных уравнений с параметрами
0,5
0,5
2.4
Практическая работа по теме: «Решение задач с параметрами на основе свойств линейных уравнений и неравенств»
1
3.
Решение задач на основе теоремы о существовании корней квадратного трехчлена
5
1
3
3.1
Исследование квадратных уравнений с параметром
0,5
0,5
3.2
Решение квадратных уравнений с параметром
0,5
0,5
3.3
Применение теорем Виета для выяснения знаков корней квадратного трехчлена
0,5
0,5
3.4
Расположение корней квадратного трехчлена
0,5
0,5
3.5
Практическая работа по теме: «Решение уравнений с параметром сводящихся к квадратным»
0,5
3.6
Практическая работа по теме: «Квадратные уравнения с параметром»
0,5
4.
Исследование и решение систем линейных уравнений
4
1
3
4.1
Исследование систем линейных уравнений
0,5
0,5
4.2
Решение систем линейных уравнений
0,5
0,5
4.3
Практическая работа по теме: «Исследование систем линейных уравнений»
2
5.
Линейные неравенства с параметрами
2
0,5
1,5
5.1
Исследование и решение неравенств с параметрами вида ах > b
0,5
0,5
5.2
Практическая работа
1
6.
Исследование и решение неравенств второй степени с параметрами
3
1
2
6.1
Исследование и решение неравенств второй степени с параметрами
1
1
6.2
Практическая работа по теме: «Неравенства второй степени с параметрами»
1
7.
Фазовая плоскость
3
1
2
7.1
Понятие фазовой плоскости
0,5
0,5
7.2
Решение уравнений с применением метода «Фазовая плоскость»
0,5
0,5
7.3
Практическая работа по теме: «Фазовая плоскость»
1
8.
Решение задач на повторение по темам данного курса
4
1
1
8.1-8.4
Решение задач
1
3
8.5
Заключительное занятие
1
Структура программы:
Тема 1. Задачи с параметрами. Основные сведения (1 часа)
Занятие 1. Что такое параметр? Что означает решить задачу с параметром? Основные типы задач с параметрами. Основные методы решения задач с параметром.
Методы обучения: лекция, объяснение, выполнение тренировочных упражнений.
Формы контроля: проверка задач самостоятельного решения.
Тема 2. Линейные уравнения с параметрами (4 часа)
Занятие 2. Первые представления о решении уравнений с параметром.
Методы обучения: лекция, рассказ, объяснение, решение задач.
Формы контроля: фронтальный опрос, проверка задач самостоятельного решения.
Занятие3. Простейшие линейные уравнения с параметром.
Методы обучения: лекция, рассказ, объяснение, решение задач.
Формы контроля: фронтальный опрос, проверка задач самостоятельного решения.
Занятие 4. Простейшие линейные уравнения с параметром.
Методы обучения: лекция, рассказ, объяснение, решение задач.
Формы контроля: фронтальный опрос, проверка задач самостоятельного решения.
Занятие 5. Практическая работа по теме: «Решение задач с параметрами на основе свойств линейных уравнений»
Методы обучения: решение задач, творческие задания.
Формы контроля: проверка задач самостоятельного решения.
Тема 3. Решение задач на основе теоремы о существовании корней квадратного трехчлена (5часов)
Занятие 6. Исследование квадратных уравнений с параметром
Методы обучения: лекция, рассказ, объяснение, решение задач.
Формы контроля: фронтальный опрос, проверка задач самостоятельного решения.
Занятие 7. Решение квадратных уравнений с параметром
Методы обучения: лекция, рассказ, объяснение, решение задач.
Формы контроля: фронтальный опрос, проверка задач самостоятельного решения.
Занятие 8. Применение теорем Виета для выяснения знаков корней квадратного трехчлена
Методы обучения: лекция, рассказ, объяснение, решение задач
Занятие 9. Расположение корней квадратного трехчлена
Методы обучения: лекция, рассказ, объяснение, решение задач.
Формы контроля: фронтальный опрос, проверка задач самостоятельного решения.
Занятие 10. Практическая работа по темам: «Решение уравнений с параметром сводящихся к квадратным» и «Квадратные уравнения с параметром»
Методы обучения: решение задач.
Формы контроля: фронтальный опрос, проверка задач самостоятельного решения, творческие задания.
Тема 4. Исследование и решение систем линейных уравнений (4 часа)
Занятие 11. Исследование систем линейных уравнений
Методы обучения: лекция, рассказ, объяснение, решение задач.
Формы контроля: фронтальный опрос, проверка задач самостоятельного решения.
Занятие 12. Решение систем линейных уравнений
Методы обучения: решение задач.
Формы контроля: фронтальный опрос, проверка задач самостоятельного решения.
Занятие 13, 14. Практическая работа по теме: «Исследование систем линейных уравнений»
Методы обучения: решение задач.
Формы контроля: фронтальный опрос, проверка задач самостоятельного решения, проверка творческих заданий.
Тема 5. Линейные неравенства с параметрами (2 часа)
Занятие 15. Исследование и решение неравенств с параметрами вида ах > b
Методы обучения: лекция, рассказ, объяснение, решение задач.
Формы контроля: фронтальный опрос, проверка задач самостоятельного решения.
Занятие 16. Практическая работа по теме: «Линейные неравенства с параметрами»
Методы обучения: решение задач.
Формы контроля: фронтальный опрос, проверка задач самостоятельного решения, проверка творческих заданий.
Тема 6. Исследование и решение неравенств второй степени с параметрами (3 часа)
Занятие 17, 18. Исследование и решение неравенств второй степени с параметрами
Методы обучения: лекция, рассказ, объяснение, решение задач.
Формы контроля: фронтальный опрос, проверка задач самостоятельного решения.
Занятие 19. Практическая работа по теме: «Неравенства второй степени с параметрами»
Методы обучения: решение задач.
Формы контроля: фронтальный опрос, проверка задач самостоятельного решения, проверка творческих заданий.
Тема 7. Фазовая плоскость (3 часа)
Занятие 20. Понятие фазовой плоскости
Методы обучения: лекция, рассказ, объяснение.
Формы контроля: проверка задач самостоятельного решения.
Занятие 21. Решение уравнений с применением метода «Фазовая плоскость»
Методы обучения: лекция, рассказ, объяснение, решение задач.
Формы контроля: фронтальный опрос, проверка задач самостоятельного решения.
Занятие 22. Практическая работа по теме: «Фазовая плоскость»
Методы обучения: лекция, рассказ, объяснение, решение задач.
Формы контроля: фронтальный опрос, проверка задач самостоятельного решения.
Тема 8. Решение задач на повторение по темам данного курса (4 часов)
Занятие 23. Решение задач
Методы обучения: решение задач, творческие задания.
Формы контроля: фронтальный опрос, проверка задач самостоятельного решения и творческих работ.
Занятие 24. Решение задач
Методы обучения: решение задач, творческие задания.
Формы контроля: фронтальный опрос, проверка задач самостоятельного решения и творческих работ
Занятие 25. Решение задач
Методы обучения: решение задач, творческие задания.
Формы контроля: фронтальный опрос, проверка задач самостоятельного решения и творческих работ
Методы обучения: лекция, рассказ, объяснение, решение задач.
Формы контроля: фронтальный опрос, проверка задач самостоятельного решения.
Занятие 26. Заключительное занятие
Решение задач с параметром на применение различных методов. Защита проектов.
Методическое обеспечение
Занятия по данной программе состоят из теоретической и практической части. Причем большее количество времени занимает практическая часть.
На занятиях дети знакомятся с различными способами решения задач с параметром, выходящими за пределы школьной программы.
Умение решать задачи - интегрированный показатель того, насколько учащийся владеет математическим материалом. Поэтому решение задач является не только одним из ведущих методов обучения, но и самым информативным способом контроля. Процесс усвоения знаний может быть условно разделен на четыре этапа:
-
понимание,
-
запоминание,
-
применение в «стандартных» условиях,
-
применение в новых, нестандартных условиях и различных сочетаниях.
На всех этих этапах для обучения и контроля могут использоваться различные типы задач. В настоящее время особенно востребованными являются умения решать задачи на самом сложном этапе - задачи математических олимпиад.
Эффективным для разностороннего развития детей является такое введение теоретического материала, которое вызвано требованиями творческой практики. Ученик должен уметь сам сформулировать задачу, и новые знания теории помогут ему в процессе решения этой задачи. Данный метод позволяет на занятии сохранить высокий творческий тонус при обращении к теории и ведет к более глубокому ее усвоению.
Важным условием придания обучению проблемного характера является подбор изучаемого материала. Каждый последующий этап должен включать в себя какие-то новые, более сложные задания, требующие теоретического осмысления.
Прохождение каждой теоретической новой темы предполагает постоянное повторение изученных тем, обращение к которым диктует практика. Такие методические приемы, как «забегание вперед», «возвращение к пройденному» придают объемность «линейному», последовательному изложению материала в данной программе, что способствует лучшему ее усвоению.
Все методы решения задач можно условно разделить на две группы: метод последовательных приближений и системный подход. Однако независимо от подхода в решении любой задачи выделяют четыре основных этапа.
Самый главный этап - анализ условия задачи. Применительно к математической задаче учащийся должен понять суть происходящих процессов и составить математическую модель реальной ситуации. Часто решение задачи уже заканчивается уже при возникновении затруднений на этом этапе, так как учащимся не хватает простой суммы знаний (незнание формул, определений, свойств). Очень много трудностей возникает у учащихся, если в задаче необходимо действовать нестандартно.
Второй - составление метода решения. На этом этапе основные сложности решения задач связаны с применением соответствующих формул, алгоритмов. Именно поиск способа или метода решения - основная трудность.
На третьем этапе выполняется решение. Здесь наиболее часты ошибки в вычислениях и незнание правил или формул.
Четвертый этап - проверка решения. Этот этап решения задач учащимися просто игнорируется.
Учащиеся, решая задачу, действуют по определенному алгоритму. После выполнения нескольких задач одного типа они прочно усваивают порядок действий и впоследствии могут применять его не только при решении подобных задач. Приобретенные знания они применяют при решении новых задач, так как начинают понимать, что во многих случаях при выполнении заданий по математике используются исходные приемы и одинаковые или похожие формулы, при расчетах выполняются одинаковые действия.
Прием объяснения ребенком собственных действий, а также Прием совместного обсуждения вопросов, возникающих по ходу работы, с педагогом или другими детьми (при индивидуально-групповой форме занятий) помогают расширить представления о средствах, способах, методах решения экзаменационных задач и тем самым способствуют развитию умения мотивированно отказываться от образца, искать оригинальные решения.
Среди методов, направленных на стимулирование творческой деятельности, можно выделить методы, связанные непосредственно с содержанием этой деятельности, а также методы, воздействующие на нее извне путем создания на занятиях обстановки, располагающей к творчеству: подбор творческих заданий, проблемная ситуация, разнообразие форм урочной деятельности, создание на занятиях доброжелательного психологического климата, индивидуальный подход.
Очевидно, что практическая реализация Концепции модернизации Российского образования невозможна без эффективного использования информационных и коммуникативных технологий. Информационная поддержка образовательного процесса может осуществляется только при наличии разнообразных компьютерных программ учебного назначения. Используется обучающая программа «1С: Репетитор. Математика», что позволяет информационный материал давать учащимся в качестве самостоятельной подготовки.
Реализацию содержания предпочтительно осуществлять на основе технологий проблемного обучения и проектной технологии. Данный курс поможет формированию познавательной, информационной, коммуникативной, рефлексивной компетентностей.
Во время реализации программы используются различные справочные материалы.
Литература для учителя
1. Шевелева Н.В. Математика. 9 класс. Учебная книга: пособие для учащихся общеобразовательных учреждений. М.: Национальное образование, 2011 г.
2. Сборник программ курсов по выбору по математике и информатике для предпрофильной подготовки учащихся. Волгоград: Изд-во ВГИПК РО, 2005
3. Г.А.Ястребинецкий Уравнения и неравенства, содержащие параметры. М., «Просвещение»1997
4. Учебно-методическая газета «Математика» № 4; 17
5. Научно-методический журнал «Математика в школе» №6
Приложение
Тема 1. Задачи с параметрами. Основные сведения
Цели: Рассмотрение понятия параметра в уравнениях и неравенствах. Формирование навыков решения задач с параметром.
-
Вводная лекция.
-
Что такое параметр?
Если рассмотреть основные уравнения, например: , то можно обратить внимание, что при поиске их корней значения остальных переменных, входящих в уравнения, считаются фиксированными и заданными.
Определение. Параметром называется независимая переменная, значение которой в задаче считается заданным фиксированным или произвольным действительным числом, или числом, принадлежащим заранее оговоренному множеству.
-
Что означает решить задачу с параметром?
Решение задачи с параметром зависит от вопроса в задаче. Если, например, требуется решить уравнение, неравенство, их систему или совокупность, то это означает предъявить обоснованный ответ либо для любого значения параметра, принадлежащего заранее оговоренному множеству.
Если же требуется найти значение параметра, при котором множество решений уравнения, неравенства удовлетворяет объявленному условию, то решение задачи и состоит в поиске указанных значений параметра.
Тема 2. Решение задач с параметрами на основе свойств линейных уравнений и неравенств
Цели: Формирование навыков решения уравнений с параметром.
-
Решение линейных уравнений с параметром.
Уравнения вида, где и - выражения, зависящие только от параметров, а - неизвестное, называется линейным уравнением относительно .
Оно приводится к виду и при имеет единственное решение при каждой системе допустимых значений параметров т.е. ( и действительны).
При и - любое число, а при и решения нет.
Пример 1. Решите при всех
Чтобы найти значение , в данном случае надо разделить уравнение на . При всех ли значениях мы можем разделить уравнение на ? Нет. При выражение обращается в 0, поэтому значение параметра является «особым», контрольным значением параметра. Рассмотрим это значение отдельно.
При - решений нет.
При .
Ответ: при ø; при .
Пример 2. Решите уравнение
или
является линейным относительно . Оно имеет смысл при любых действительных значениях параметра .
Приведя его к виду заметим, что при оно принимает вид: т.е. решением его служит любое действительное число, уравнение имеет вид: т.е. не имеет решения.
При уравнение имеет единственное решение
Ответ: при любое действительное число
при ø
при
Пример 3. Решить уравнение
(1)
Так как знаменатель не должен быть равен нулю, то
Знаменатели алгебраических дробей равны, следовательно, для того, чтобы выполнялось равенство (1), должны быть равны и числители:
Мы выразили неизвестное через параметр , но для есть ограничение , т.е.
откуда
При исходное уравнение решений не имеет. Так как при подстановке данного значения в исходное уравнение получаем для значение -7, которое не входит в область допустимых значений.
Ответ: при
при нет корней.
2. Самостоятельное решение уравнений с параметром:
1)
2)
3)
4)
5)
6)
7)
8)
9) ;
10)
11)
12)
2. Простейшие линейные неравенства с параметром
Цели: Формирование навыков решения линейных неравенств с параметром.
Каждое из неравенств вида > < или где и - действительные числа или функции от параметров, а - действительная переменная величина, называется линейным неравенством с одним неизвестным .
Пример 1. Неравенство < - линейное относительно .
При - любое число,
при >1 <
при <1 > .
2. Самостоятельное решение неравенств с параметром:
Задания для самостоятельного решения линейных неравенств:
1) < 5;
2) > 6;
3)
4)
5) <
6) <
7) < ;
8) <
3. Практическая работа по теме:
«Решение задач с параметрами на основе свойств линейных уравнений и неравенств»
Цели: проверка степени усвоения учащимися изученного материала и умения применять его при решении задач.
-
Организация учащихся на выполнение работы.
-
Выполнение трехуровневой самостоятельной работы.
1-й уровень. Решите линейные уравнения и неравенства (- параметр)
1)
2)
3) >
2-й уровень. Решите линейные уравнения и неравенства
(- параметр)
1)
2)<
3)
3-й уровень. Решите линейные уравнения и неравенства
(- параметр)
1)
2)
3) При каких значениях параметра корень уравнения является неотрицательным числом?
Тема 3. Решение задач на основе теоремы о существовании корней квадратного трехчлена
Цели: Формирование начальных навыков решения задач по данной теме
-
Объяснение новой темы.
Уравнение вида где - неизвестное, - выражение, зависящие только от параметров, и называется квадратным уравнением относительно .
Допустимыми будем считать только те значения параметров, при которых - действительны.
Пример 1. Определите все значения параметра, при которых уравнение имеет один корень:
-
при - один корень;
-
при один корень возможен, если
, решив данное квадратное уравнение, получим корни:
Ответ:
Пример 2. Решите уравнение:
-
при ø;
-
при и то существует два корня.
2. Самостоятельное решение уравнений с параметром:
Решить уравнения относительно :
1)
2)
3) Определите все значения параметра , при которых уравнение имеет один корень:
4)
5)
6)
7)
Тема 4. Исследование квадратного трехчлена
Цели: Формирование у учащихся исследовательских навыков у учащихся
1. Объяснение материала
Функция, задаваемая формулой, где называется квадратичной функцией. Графиком квадратичной функции является парабола. Точка графика с абсциссой называется вершиной параболы, ордината этой точки равна
При > 0 «ветви» параболы направлены вверх, а при < 0 - вниз. Каждый из этих двух случаев разбивается на три подслучая в зависимости от числа корней уравнения.
При > 0 уравнение имеет два действительных корня
При уравнение имеет один корень
При < 0 уравнение не имеет действительных корней.
Пример 1. При каких область значений функции содержит отрезок :
1)
- линейная функция, то то
2) > 0
- квадратичная функция, графиком является парабола, «ветви» которой направлены вверх, то
, .
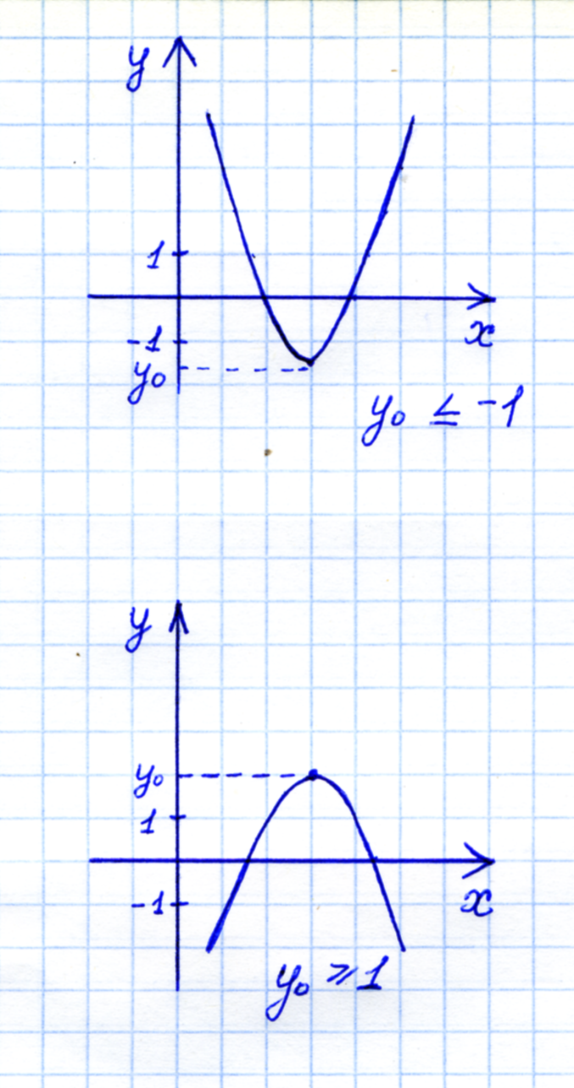
при .
3) < 0
- квадратичная функция, графиком является парабола, «ветви» которой направлены вниз, то

< 0,
После объединения решений получаем: .
2. Самостоятельное решение уравнений с параметром:
1)Выяснить, при каких значениях параметра, а оба корня уравнения меньше единицы.
2) Выяснить, при каких значениях к для уравнения ?
3) Выяснить, при каких значениях параметра, а оба корня уравнения больше 0,5?
4) Исследуйте уравнение на знаки корней в зависимости от значений параметра а.
Тема 5. Фазовая плоскость
Цели: Формирование навыков решения уравнений с параметром графическим методом
1. Объяснение новой темы
Рассмотренные до этого стандартные способы решения уравнений и неравенств в отдельных случаях приводит к сложным и утомительным преобразованиям. Процесс решения может быть иногда упрощен, если применить метод «Фазовая плоскость»
Пример 1. Определите, сколько корней имеет уравнение в зависимости от параметра а:
< 0 - нет решений;
- четыре корня;
- три корня;
> 4 - два корня.
Задачи для самостоятельного решения:
Определите, сколько корней имеет уравнение в зависимости от параметра а:
1) ; 2);
3) ; 4) ;
5) ; 6) ;
7) ; 8)