Конспект уроку з геометрії

Тема програми: «Паралельність прямих і площин у просторі»

Тема уроку: Розв'язування вправ з теми: «Аксіоми стереометрії. Наслідки з аксіом стереометрії»

Мета: узагальнити, систематизувати та закріпити знання учнів щодо застосування аксіом та їх наслідків в ході розв'язування задач, забезпечувати умови для досягнення кожним учнем практичної компетентності розв'язання задач. Розвивати логічне мислення, просторову уяву,увагу, вміння зображати та виконувати малюнки геометричних фігур у просторі кмітливість, силу волі. Виховувати самостійність, наполегливість.

Тип уроку: узагальнення і систематизації знань.

Організація навчальної діяльності учнів: урок - бенефіс

Методи навчання, прийоми: робота біля дошки, робота за малюнком, тестування, виконання завдань на відповідність, розв'язування задач, аукціон ідей.

Основні терміни і поняття: аксіома, точка, пряма, площина.

Навчально - дидактичне забезпечення:

ХІД УРОКУ

І. Організаційна частина. Вступне слово викладача.(1)

Вітання. Налаштування на роботу. Запис теми уроку. (мета уроку озвучує викладач: узагальнити, систематизувати знання щодо застосування аксіом та їх наслідків під час розв'язування задач. Показати значущість аксіом та їх наслідків не лише в геометрії, а й їх практичне застосування в житті людини)

ІІ. Мотивація навчальної діяльності. (2)

Погляньте за вікно. Осінь. Пасмурно, дождливо …. А так хочеться чогось позитивного. Правда? Пропоную вам створити букет, щоб підняти собі настрій. Він буде складатися з квіток. У вас на партах лежать серцевинки від них, протягом уроку вам потрібно назбирати якомога більше пелюсток, щоб ваша квітка вийшла найкращою.

ІІ. Перевірка домашнього завдання. (5)

Робота біля дошки.

До дошки запрошується учень. Завдання: відобразити способи завдання площини.

Способи задання площини.

• трьома точками, які не лежать на одній прямій (рис. 3.2.а.);

• прямою і точкою, яка не лежить на прямій (рис. З.2.6.);

• двома прямими, що перетинаються (рис. З.2.В.);

• двома паралельними прямими (рис. 3.2.г.);

• плоскою фігурою (наприклад, трикутником АВС, рис. З.2.Д.);

• слідами (рис. 3.2.є.).

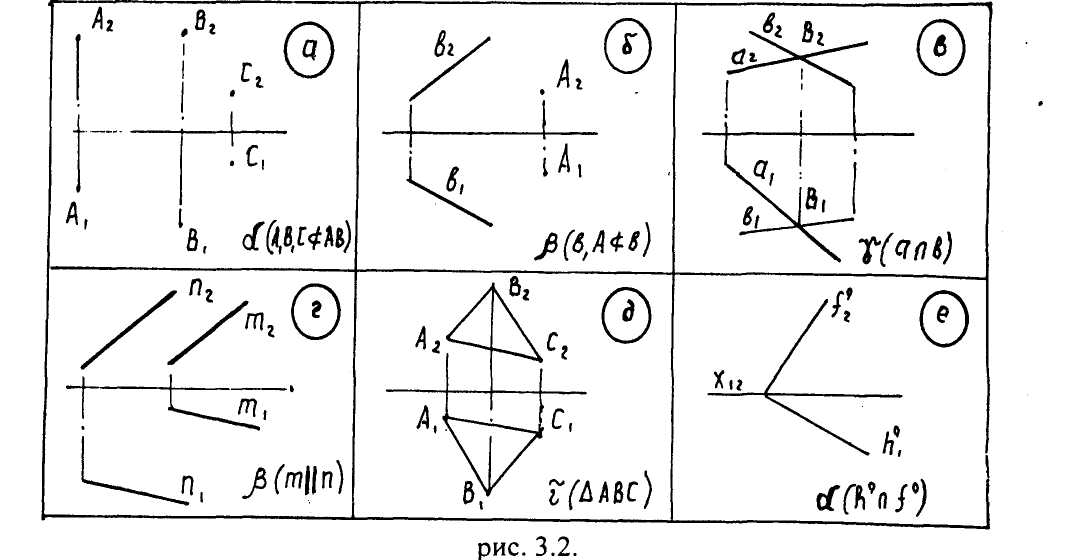
Оцінювання: правильна відповідь 2 бали.

IІІ. Узагальнення і систематизація ЗУН. (25)

Робота біля дошки.

І. Сформулювати аксіоми стереометрії за допомогою малюнків. (1 учень біля дошки).

ІІ. Встановити відповідність. (1 учень біля дошки).

- Через три точки, які не лежать на одній прямій, можна провести площину і до того ж одну.

- Якщо дві точки прямої належать площині, то вся пряма належить цій площині.

- Через пряму і точку, яка не лежить на ній, можна провести площину і до того ж одну.

- Площина розбиває простір на два півпростори.

Робота за малюнком

ІІІ. Про що говорить малюнок. (всі учні групи)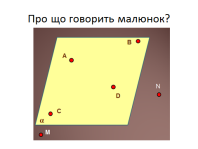

Викладач демонструє за допомогою слайдів малюнки до аксіом стереометрії, а учні формулюють їх. (див. час - прочитати запис на картках )

Оцінювання: правильна відповідь 1 бал.

Перевірка роботи учнів біля дошки.

Оцінювання: правильна відповідь 2 бали.

Робота за малюнком.(усно).

Тестування. Завдання на відповідність.

(формат ЗНО)

Викладач пропонує учням два типи завдань.

Учні день народження яких кратне 2 отримують тестові завдання, а всі інші працюють з викладачем - робота за малюнком. (5хв).

Потім учні, які виконували тестування працюють з викладачем, а решта виконують завдання на відповідність.

Оцінювання: правильна усна відповідь 2 бали. Тестування і відповідність в 3 бали.

Тестові завдання.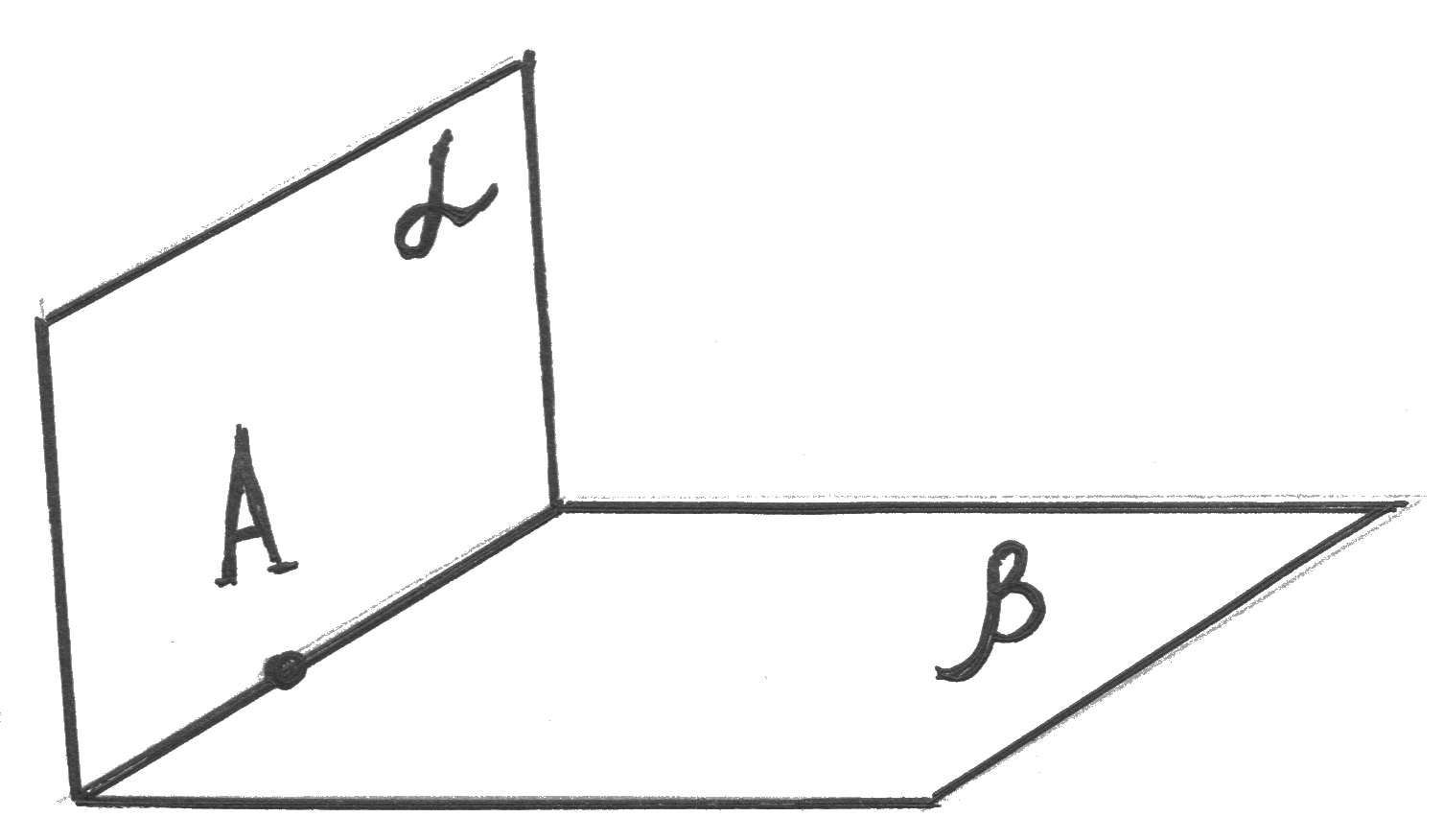

1) Назвіть за малюнком аксіому стереометрії.

Виберіть одну правильну відповідь.

А) аксіома С₁; б) аксіома С₂; в) аксіома С₃; г) інша відповідь.

2) Продовжить речення:

Стереометрія - це розділ геометрії, в якому:

а) вивчають фігури на площині;

б) вивчають фігури на площині і просторі;

в) вивчають фігури у просторі;

г) інша відповідь.

3)Виберіть неправильний варіант відповіді: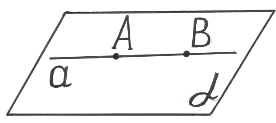

Єдину площину можна провести через:

а) пряму і точку, яка не лежить на ній;

б) пряму і точку, що лежить на ній;

в) через три точки, що не лежать на одній прямій;

4) Назвіть спільну пряму площин AFD і DEF.

А) AD; б) DE; в) DF; г) AF.

5) Назвіть за малюнком теорему:

а) Яка б не була площина існують точки, які належать цій площині і які їй не належать.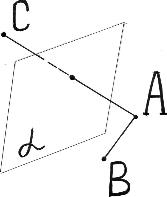

Б) Через три точки, які не лежать на одній прямій можна провести площину і до того тільки одну.

В) Якщо дві точки прямої належать площині, то вся пряма належить цій площині.

Г) Інша відповідь.

6) Виберіть неправильний варіант відповіді(за малюнком)

А) Точки А і В належать одному півпростору;

Б) Точки А і С належать різним півпросторам;

В) Точки А і С належать одному півпростору

Г) точки А і В не співпадають.

Ключ: 1б,2в,3а,4в,5в,6в.

Завдання на відповідністьЯкщо три точки А, В, С лежать на одній прямій, то через них можна провести…

У просторі задано дві прямі а і в які перетинаються в точці О. Через прямі а і в можна провести …

Чотири точки А, В, С, D не лежать в одній площині. Площини АВС і ABD перетинаються по прямій …

Точки А, В, С, D не лежать в одній площині. Площини АВD і BCD перетинаютьсяпо прямій …

Назвіть приклади практичного застосування аксіом стереометрії.

А. АВ

Б. тільки одну площину

В. Дві різні площини

Г. BD

Д. безліч площин

Ключ: 1д,2б,3а,4г

Учні виконують взаємоперевірку.

</ Розв'язування задач біля дошки

Задача 1

Чи можна через точку перетину двох даних прямих провести третю пряму, яка не лежить з ними в одній площині? Відповідь поясніть.

Етапи розв'язування задачі:

1.Яку аксіому можна застосувати, маючи дві прямі, що перетинаються?

2.Візьміть точку, яка не належить площині перетину двох прямих. Яку аксіому можна застосувати в цьому випадку?

3. Яка умова необхідна для проведення прямої? Чи є в нас така умова?

4. Висновок.

Задача 2

Пряма АВ і точки С, D не лежать в одній площині. Доведіть, прямі АВ і СD не перетинаються.

Підказка для доведення

Застосуйте метод доведення від супротивного. Ваші ідеї, щодо розв'язування? Які аксіоми можна застосувати?

Задача 3

Прямі а і b перетинаються в точці А. Доведіть, що пряма с, яка перетинає дані прямі і не проходить через точку А, лежить з ним в одній площині.

V. Домашнє завдання.(3)

Завдання на вибір:

1.Дано пряму а і точку А, що не лежить на цій прямій. Доведіть, що пряма с, яка проходить через точку А і перетинає пряму а, лежи з ними в одній площині.

2.Точки А, В і пряма СD не лежать в одній площині. Доведіть, і прямі АС і ВD не перетинаються.

VІ. Підбиття підсумків уроку. Рефлексія.( (5)

А зараз пропоную вам провести аукціон ідей відповівши на питання: де ж можна зустріти застосування аксіом та їх наслідків в житті і діяльності людей. Час на обмірковування 1 хв. Оцінювання 5 балів.

А зараз створимо наш букет і поглянемо, які ж оцінки ви отримали за сьогоднішній урок.

через три точки,

якщо дві точки прямої належать площині,

через пряму і точку,

площина

які не лежать на одній прямій,

яка не лежить на ній,

розбиває простір

можна провести площину

належить цій площині.

площину і до того ж одну.

на два півпростори.

то вся пряма

можна провести

і до того ж одну.

Тестові завдання.

1) Назвіть за малюнком аксіому стереометрії.

Виберіть одну правильну відповідь.

А) аксіома С₁; б) аксіома С₂; в) аксіома С₃; г) інша відповідь.

2) Продовжить речення:

Стереометрія - це розділ геометрії, в якому:

а) вивчають фігури на площині;

б) вивчають фігури на площині і просторі;

в) вивчають фігури у просторі;

г) інша відповідь.

3)Виберіть неправильний варіант відповіді:

Єдину площину можна провести через:

а) пряму і точку, яка не лежить на ній;

б) пряму і точку, що лежить на ній;

в) через три точки, що не лежать на одній прямій;

4) Назвіть спільну пряму площин AFD і DEF.

А) AD; б) DE; в) DF; г) AF.

5) Назвіть за малюнком теорему:

а) Яка б не була площина існують точки, які належать цій площині і які їй не належать.

Б) Через три точки, які не лежать на одній прямій можна провести площину і до того тільки одну.

В) Якщо дві точки прямої належать площині, то вся пряма належить цій площині.

Г) Інша відповідь.

6) Виберіть неправильний варіант відповіді(за малюнком)

А) Точки А і В належать одному півпростору;

Б) Точки А і С належать різним півпросторам;

В) Точки А і С належать одному півпростору

Г) точки А і В не співпадають.

Тестові завдання.

1) Назвіть за малюнком аксіому стереометрії.

Виберіть одну правильну відповідь.

А) аксіома С₁; б) аксіома С₂; в) аксіома С₃; г) інша відповідь.

2) Продовжить речення:

Стереометрія - це розділ геометрії, в якому:

а) вивчають фігури на площині;

б) вивчають фігури на площині і просторі;

в) вивчають фігури у просторі;

г) інша відповідь.

3)Виберіть неправильний варіант відповіді:

Єдину площину можна провести через:

а) пряму і точку, яка не лежить на ній;

б) пряму і точку, що лежить на ній;

в) через три точки, що не лежать на одній прямій;

4) Назвіть спільну пряму площин AFD і DEF.

А) AD; б) DE; в) DF; г) AF.

5) Назвіть за малюнком теорему:

а) Яка б не була площина існують точки, які належать цій площині і які їй не належать.

Б) Через три точки, які не лежать на одній прямій можна провести площину і до того тільки одну.

В) Якщо дві точки прямої належать площині, то вся пряма належить цій площині.

Г) Інша відповідь.

6) Виберіть неправильний варіант відповіді(за малюнком)

А) Точки А і В належать одному півпростору;

Б) Точки А і С належать різним півпросторам;

В) Точки А і С належать одному півпростору

Г) точки А і В не співпадають.

Завдання на відповідністьЯкщо три точки А, В, С лежать на одній прямій, то через них можна провести…

У просторі задано дві прямі а і в які перетинаються в точці О. Через прямі а і в можна провести …

Чотири точки А, В, С, D не лежать в одній площині. Площини АВС і ABD перетинаються по прямій …

Точки А, В, С, D не лежать в одній площині. Площини АВD і BCD перетинаютьсяпо прямій …

Назвіть приклади практичного застосування аксіом стереометрії.

А. АВ

Б. тільки одну площину

В. Дві різні площини

Г. BD

Д. безліч площин

Завдання на відповідністьЯкщо три точки А, В, С лежать на одній прямій, то через них можна провести…

У просторі задано дві прямі а і в які перетинаються в точці О. Через прямі а і в можна провести …

Чотири точки А, В, С, D не лежать в одній площині. Площини АВС і ABD перетинаються по прямій …

Точки А, В, С, D не лежать в одній площині. Площини АВD і BCD перетинаютьсяпо прямій …

Назвіть приклади практичного застосування аксіом стереометрії.

А. АВ

Б. тільки одну площину

В. Дві різні площини

Г. BD

Д. безліч площин

Завдання на відповідністьЯкщо три точки А, В, С лежать на одній прямій, то через них можна провести…

У просторі задано дві прямі а і в які перетинаються в точці О. Через прямі а і в можна провести …

Чотири точки А, В, С, D не лежать в одній площині. Площини АВС і ABD перетинаються по прямій …

Точки А, В, С, D не лежать в одній площині. Площини АВD і BCD перетинаютьсяпо прямій …

Назвіть приклади практичного застосування аксіом стереометрії.

А. АВ

Б. тільки одну площину

В. Дві різні площини

Г. BD

Д. безліч площин

Завдання на відповідністьЯкщо три точки А, В, С лежать на одній прямій, то через них можна провести…

У просторі задано дві прямі а і в які перетинаються в точці О. Через прямі а і в можна провести …

Чотири точки А, В, С, D не лежать в одній площині. Площини АВС і ABD перетинаються по прямій …

Точки А, В, С, D не лежать в одній площині. Площини АВD і BCD перетинаютьсяпо прямій …

Назвіть приклади практичного застосування аксіом стереометрії.

А. АВ

Б. тільки одну площину

В. Дві різні площини

Г. BD

Д. безліч площин

Завдання на відповідністьЯкщо три точки А, В, С лежать на одній прямій, то через них можна провести…

У просторі задано дві прямі а і в які перетинаються в точці О. Через прямі а і в можна провести …

Чотири точки А, В, С, D не лежать в одній площині. Площини АВС і ABD перетинаються по прямій …

Точки А, В, С, D не лежать в одній площині. Площини АВD і BCD перетинаютьсяпо прямій …

Назвіть приклади практичного застосування аксіом стереометрії.

А. АВ

Б. тільки одну площину

В. Дві різні площини

Г. BD

Д. безліч площин