Открытая устная региональная олимпиада по математике.

18 декабря 2011г.

7 класс-РЕШЕНИЯ

1. Из спичек выложено неверное равенство:

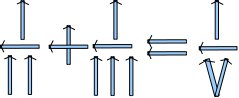
Переложите одну спичку так, чтобы равенство стало верным.

Решение. .

2. Анастасия Васильевна купила задачник, в котором собраны 200 задач заключительного этапа Всероссийской Олимпиады, и решила прорешать эти задачи за три дня. В первый день она решила половину всех задач, которые смогла решить за все три дня. Во второй день она решила на 60 задач меньше, чем в первый, а в третий вполовину меньше, чем в первый и во второй вместе. Сколько задач не смогла решить Анастасия Васильевна?

Ответ: 20. Решение. Пусть всего было решено n задач. Тогда по условию . Решив уравнение, получаем . Тогда Анастасия Васильевна не решила 200 - 180 = 20 задач.

3. Стороны квадрата ABCD равны 6 см. На сторонах BC и CD отметили точки P и Q такие, что отрезки AP и AQ делят квадрат на три части равной площади. Найдите площадь треугольника APQ.

Ответ: 10 см². Решение. из условия ясно, что . С другой стороны, площадь прямоугольного треугольника равна половине произведения катетов, поэтому , откуда . Аналогично , значит и . Отсюда см.

4. Найдите наименьшее пятизначное число, делящееся на 9, в записи которого все цифры различны.

Ответ: 10269. Решение 1. Рассмотрим наименьшее такое число. На первом его месте стоит цифра 1 (иначе наше число меньше). Аналогично, на вторых и третьих местах стоят цифры 0 и 2. Кроме того, сумма цифра цифр должна делится на 9. На предпоследнем месте должно стоять одно из чисел 3, 4, 5, 6 (большие противоречат минимальности). Несложным перебором убеждаемся, что случаи 3, 4, 5 невозможны, а для 6 на последнем месте может стоять только 9.

Решение 2. Минимальное пятизначное число со всеми различными цифрами - это 10234. Минимальное число, не меньшее данного и делящееся на 9, есть 10242. Если к этому числу мы трижды прибавим по 9, мы получим числа 10251, 10260, 10269. Из них только последнее удовлетворяет условию задачи, т.к. все его цифры различны, и, по построению, оно делится на 9.

5. Сколько всего имеется шестизначных чисел abcdef со всеми различными цифрами 1, 2, 3, 4, 5, 6 таких, что двузначное число ab делится на 2, трёхзначное число abc делится на 3, четырёхзначное число abcd делится на 4, пятизначное число abcde делится на 5, шестизначное число abcdef делится на 6?

Ответ: 2. Решение. Чётные цифры стоят на чётных местах, поэтому нечётные - на нечётных. На пятом месте стоит цифра 5. Значит, сумма a + c всегда 1 + 3 = 4. Сумма первых трех цифр делится на 3, значит вторая цифра - это только 2. Т.к abcd делится на 4, то cd делится на 4, и d может быть только 6. Получаем 2 варианта: 123654 и 321654, каждый из которых подходит под условие задачи.

6. На плоскости отмечена точка A. Андрей и Борис играют в следующую игру. Они ходят по очереди (первым начинает Андрей); за один ход разрешается провести на этой плоскости через точку A прямую. Проводимая прямая не должна совпадать ни с одной из прямых, проведённых игроками на предыдущих ходах. Проигрывает тот, после хода которого угол между какими-то из проведённых прямых окажется меньше 1^o. Может ли кто-либо из игроков гарантировать себе победу вне зависимости от игры соперника?

Ответ: да, победит Борис. Решение. каждым своим ходом Борис проводит прямую, перпендикулярную к проведённой последним ходом Андрея прямой. Тем самым он гарантирует себе возможность хода. Если от противного, после хода Бориса новая прямая l образует угол, меньший 1^o с одной из ранее проведённых прямых s, тогда ранее уже образовывался угол, меньший 1 ^o между прямыми, перпендикулярными к l и s, что противоречит тому, что до Бориса дошла очередь хода. Следовательно, Андрей проиграет, так как всего можно провести не более 180 прямых.

6. На острове Кокос проживает 2011 аборигенов, каждый из которых либо всегда говорит правду (рыцарь), либо всегда обманывает (лжец), причём они не все лжецы. Путешественник хочет узнать количество рыцарей на этом острове. Ему разрешено один раз в день собирать на берегу любую группу островитян, каждый из которых напишет количество рыцарей среди собравшихся. За какое наименьшее число дней путешественник сможет выяснить точное число рыцарей?

Ответ: 2 дня. Решение. В первый день путешественник собирает всех жителей острова, после чего они разбиваются на группы (может быть некоторые будут пусты): первая - написавшие 0 рыцарей, вторая - написавшие 1 рыцаря, третья - написавшие 2 рыцаря и т.д. С одной стороны все рыцари на собрании в первый день напишут одно и то же число, а лжецы напишут любое другое число. Во второй день из всех групп приглашаем по одному человеку, этим мы гарантируем присутствие ровно одного рыцаря на собрании. Та группа людей, представитель которой во второй день напишет единицу, и будет рыцарской, и количество человек в этой группе и есть точное число рыцарей на острове.

Ясно, что путешественник не сможет узнать количество рыцарей на острове в первый день, не позвав на собрание всех островитян. Но при этом будет невозможно отличить группу из рыцарей от группы лжецов, написавших ровно такое же число, что и их количество в группе.

6. Таблицу 5  5 заполнили натуральными числами 1, 2, ..., 25 таким образом, что каждое число встречается в таблице ровно один раз и каждые два последовательных числа находятся в соседних (таких, что имеют общую сторону) клетках. Какое максимальное количество простых чисел могло оказаться в одном столбце или строке? Приведите пример заполнения таблицы, для которого такое наибольшее значение достигается.

Ответ: 4. Решение. оценка делается так: раскрасим клетки доски в шахматном порядке, чтобы всего было 13 черных и 12 белых клеток. Тогда из условия ясно, что в любом заполнении нечетные числа должны стоять в черных клетках, а четные - в белых. В любой строке и столбце есть как минимум две белые клетки, на которых стоят четные числа. Простым среди двух четных чисел может быть только одно (двойка), поэтому в любой строке или столбце не более 4-х простых. Пример расстановки чисел с 4 простыми в среднем столбце:

21

22

23

24

25

20

19

4

5

6

17

18

3

8

7

16

1

2

9

10

15

14

13

12

11