- Учителю
- Методическая рекомендация на тему 'Рационал теңсіздіктерді интервалдау әдісімен шешу' (8 класс)
Методическая рекомендация на тему 'Рационал теңсіздіктерді интервалдау әдісімен шешу' (8 класс)
Рационал теңсіздіктерді интервалдау әдісімен шешу
Р.А.ЖУМАБЕКОВА
№13 жалпы білім беретін орта мектептің мұғалімі
Рационал теңсіздіктерді интервалдау әдісімен шешу математиканың теңсіздіктерді және теңсіздіктер жүйесін шешу, функцияны зерттеу, көрсеткіштік және логарифидік теңсіздіктерді шешу бөлімдерінде маңызды роль атқарады. Бұл әдістің негізгі мағынасы мынада:
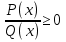 (немесе
(немесе 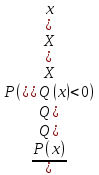 түрінде берілген рационал теңсіздіктің (мұнда P(x) және Q(x) көпмүшелік) алымы мен бөлімнің нольдік нүктелерін 0Х ociне саламыз. Басқа сөзбен айтқанда P(x)=O және Q(x)=O теңдеулерін қанағаттандыратын Х айнымалысының мәндерін абцисса ociнде белгілейміз. Табылғын нүктелер ОХ осiн бірнеше интервалдарға бөледі. Үзіліссіз функциялардың "Егер f(x) функциясы (а,в) интервалында нольге айналмайтын болса онда сол интервалда функция түрақты танбасын сақтайды"деген аса маңызды қарапайым дөнелдеуі оқулыкта бар, толық дөнелдеуі жоғары математика кустарында келтірілетін теореманың негізінде
түрінде берілген рационал теңсіздіктің (мұнда P(x) және Q(x) көпмүшелік) алымы мен бөлімнің нольдік нүктелерін 0Х ociне саламыз. Басқа сөзбен айтқанда P(x)=O және Q(x)=O теңдеулерін қанағаттандыратын Х айнымалысының мәндерін абцисса ociнде белгілейміз. Табылғын нүктелер ОХ осiн бірнеше интервалдарға бөледі. Үзіліссіз функциялардың "Егер f(x) функциясы (а,в) интервалында нольге айналмайтын болса онда сол интервалда функция түрақты танбасын сақтайды"деген аса маңызды қарапайым дөнелдеуі оқулыкта бар, толық дөнелдеуі жоғары математика кустарында келтірілетін теореманың негізінде 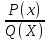 функциясының өр интервалда таңбасы өзгермейді.
функциясының өр интервалда таңбасы өзгермейді.
Ал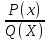 функциясының өр интервалдағы таңбасы осы интервалдан қандайда бір х-тің тиянақты мәнің функцияға қою арқылы анықталады. Шешуге ыңғайлы болу үшін бөлінді түрінде берілген теңсіздікті теңсіздік таңбасына байланысты не көбейтінді түрінде, не теңсіздіктер жүйесі түріне келтіру керек.
функциясының өр интервалдағы таңбасы осы интервалдан қандайда бір х-тің тиянақты мәнің функцияға қою арқылы анықталады. Шешуге ыңғайлы болу үшін бөлінді түрінде берілген теңсіздікті теңсіздік таңбасына байланысты не көбейтінді түрінде, не теңсіздіктер жүйесі түріне келтіру керек.
Х- а екімүшелік қарастыралық.Бұл екімүшелік а нүктесінің оң жағында жатқан кез-келген Х-тың мәні үшін оң және а нүктесінің сол жағында жатқан кех-келген Х-тың мәні үшін теріс болатыны белгілі.
-----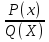 ------
------ ------
------ --------------
--------------
Осындай Х- а екімүшелігінің қарапайым рационал теңсіздіктерді интервалдар әдісімен шешуде аса маңызды роль атқарады.
(х-а1) (х-а2)... (х-0п)›0 (1) теңсіздігі берілсін.
Теңсіздіктерді интервалдар әдісімен шешу үшін келесі алгоритм қолданылады :
1)Берілген теңсіздікті Р(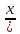 , Р(х)›0, Р(х)≥0, Р(х)≤0 түрлерінің біріне келтіреміз;
, Р(х)›0, Р(х)≥0, Р(х)≤0 түрлерінің біріне келтіреміз;
2)теңсіздіктің сол жағын нөлге теңестіріп,шыққан теңдеуді шешеміз,яғни сәйкес функцияның таңбасын аңықтап,нөлдерін табамыз;
3)теңдеудің түбірлерінің мәнін сан осіне белгілеп,сан осін интервалдарға бөлеміз;
4)интервалдың кез келген біреуінде функцияның таңбасын анықтап,осы интервалға аныкталған таңбаны қоямыз;
5)теңдеудің тубірі қайталанбаған немесе тақ рет қайталанған жағдайда қалған интервалдардағы таңбаларды кезектеп қоямыз;ал егер түбір жұп рет қайталанса,осы түбірдің екі жағындағы интервалдардың таңбаларын бірдей етіп аламыз;
6)таңбасы теңсіздік таңбасына сәйкес интервалдарды жауап ретінде аламыз.
Мысалы: 1.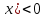 теңсіздігі берілсін.
теңсіздігі берілсін.
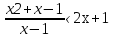 теңсіздік(1) түрге келді.
теңсіздік(1) түрге келді.
Жоғарыдағы келтірілген әдіс бойынша шешсек:
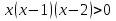
Жауабы: (0;1)υ(2,+∞)немесе 02 теңсіздік нөльден тек улкен болғандықтан,нольдік нүктелер шешімге кірмейді.
2.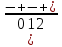
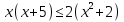
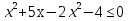
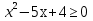
(x-1)(x-4)≥0
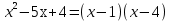
Жауабы:[-∞,1]υ[4,+∞] немесе 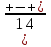 және
және 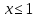
3.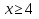 ≥0
≥0
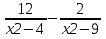
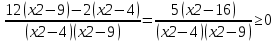
-------------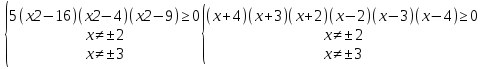
Жауабы: [-∞,-4]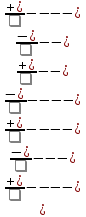 -3,-2]
-3,-2]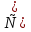
Квадрат теңсіздіктерді интервалдау әдісімен шешу үшін оларды жіктеу арқылы (1)түрге келтіріп,содан соң жоғарыдағы таныс жолмен теңсіздіктің шешімін табатындығын жоғарыдағыдан көрдік.Ал егер квадрат теңдеудің дискриминантты нольден кіші болса яғни теңдеу жіктелінбесе ондай теңсіздікті қалай шешуге болады?
Дискриминатты нольден кішіаx2+вx+c›0. a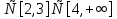 (2) теңсіздігінің шешімін табалық.
(2) теңсіздігінің шешімін табалық.
У=ах2+вх+с ох осімен қиылысатын параболы.Олай болса, а›0 параболының тармағының жоғары қарайтынын еске түсірсек онда ах2+вх+с›0 теңсіздігі х-тың кез-келген мәні үшін орындалатынын ал а‹0 болса х-тың бірде-бір мәні үшін теңсіздіктің орындалмайтынын түсіну аса қиын емес.
Яғни(2) теңсіздіктің а›0 болса шешімі -∞‹х‹∞ немесе (-∞,∞)болады. Ал а‹0 болса шешімі болмайды.
ах2+вх+с‹0, а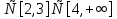 теңсіздігінің шешімінде дәл осы жолмен анықтауға болады.
теңсіздігінің шешімінде дәл осы жолмен анықтауға болады.
Мысалы:
-
2х2-1‹3х-х2-6 түрлендіру арқылы берілген теңсіздікке мәндес 2х2-3х+5‹0 теңсіздігің аламыз.бұл квадрат үшмүшелігінің дискриминнатты нольден кіші және х-тың коэффициенті нольден үлкен,яғни жоғарыдағы жасаған тұжырым бойынша теңсіздіктің шешімі болмады.
-
х2+4х‹2х2-х+7 берілгентеңсіздікке түрлендіру арқылы мәндес х2-5х+7›0 теңсіздігін аламыз.
Дискриминанты нольден кіші және х-тын коэффициенті нольден үлкен болғандықтан парабола ОХ осінен жоғары орналасады. Яғни х-тың кез-келген мәні теңсіздікті қанағаттандырады.
Шешімі (-∞,∞) немесе -∞‹х‹∞
Кейбір дәрежесі 2-ден жоғары алгебралық теңсіздіктер бірнеше арнаулы түрлендірулерден соң
(х-а1)х1(х-а2)х2... (х-ап)хп›0 (3)
түрінекеледі .Мұндағы а1,а2....,ап,а1‹а2‹...‹ап шартын қанағаттандыратын тиянақты нақты сандар,к1,к2....,кп тиянақты натурал сандар.
(3) түрдегі теңсіздіктерді, жалпылаған интервалдар әдісі арқылы шешеді. Бұл әдістің мағынасы былай болады: xо›an шартын қанағаттындыратын аралық үшін-к-ның кез-келген мәнде P(xo)›0 болады.
Ал ап-1‹х1‹ап шартын қанағаттандыратын аралықта ең соңғы көбейткіштен басқа көбейткіштердің танбалары оң болады.Ал (х-ап) көбейткішінің танбасы кп дәреже көрсеткішіне байланысты,яғни егеркп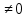 2п болса (х-ап)кп
2п болса (х-ап)кп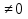 онда P(x)
онда P(x)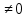 0 егер кп=2п+1болса (х-ап)кп ‹0 онда P(x)
0 егер кп=2п+1болса (х-ап)кп ‹0 онда P(x)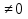 болады.
болады.
Демек P(x) көпмүшелігі ап нүктесі арқылы өткенде таңбасы ауысады егер кп жүп сан болса.
Қорыта айтқанда (3) түрдегі теңсіздіктерді шешу үшін төмендегідей жағдайларда орындау керек.
1.Сан осіне ап, а2,......., ап сандарын аламыз:
--------а,---------а2---------------------------------------ап----------
2.Ең үлкен нүктенің (ап) оң жағындағы аралыққа бірден "+" танбасын қоямыз.
3.Солға қарай келесі аралықта таңба "+" болады,егер кп жүп сан болса, "-" болады, егер кп тақ сан боласа,
4.Келесі аралықтың таңбасы ауысады егер кп-1 тақ болса, таңбасы ауыспайды егер кп-1 жүп сан болса.
Осындай тәртіппен барлық аралықтардың таңбысын анықтаймыз.
5. P(x) ›0 теңсіздігін шешімі барлық "+" таңбасы қойылған аралықтардың ал P(х)‹0 теңсіздігін шешімі барлық
"-" таңбасы қойылғын аралықтарының қосындысы болады.
Мысалы. 1. (х+3)2 (х-2) (х+5)3‹0
(х+5)3 (х+3)2 (х-2)‹0
1.Сан осіне берілген нүктелерді өсу ретімен саламыз.
----+----5------------3-----------------------------2-------------+---------------
2.х›2 аралығына жоғарыда айтылғанда "+" таңбасын қоямыз.
3. -3‹х‹2 аралығындағы көпмүшеліктің таңбасын дәрежесін 1-ге тең екенін екеріп "-" таңбасын қоямыз.
4. -5‹х‹-3 аралығында х+3 көбейткішінің дәредесі жүп болғандықтан "-" өзгермейді
5.-∞‹х‹-5 аралығында х+5 дәрежесі болғандықтан "-" "+" қа ауысады.
Яғни теңсіздік [-5,-3] [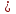 ][-3,2] аралығында орындалады
][-3,2] аралығында орындалады
Мысалы.2. 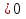 теңсіздігін шешейік.
теңсіздігін шешейік.
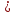 бөлшегінің тыңбасы (7-х)(х+2) көбейтіндісініңтаңбасымен дәл келетіндіктен, берілген теңсіздік
бөлшегінің тыңбасы (7-х)(х+2) көбейтіндісініңтаңбасымен дәл келетіндіктен, берілген теңсіздік
(7-х) (х+2) теңсіздігімен мәндес болады.
(7-х) (х+2)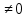 0 теңсіздігін (1) түрге келтіре отырып және интервалдар әдісін пайдалана отырып осы теңсіздіктердің шешімдерінің жиыны, яғни берілген
0 теңсіздігін (1) түрге келтіре отырып және интервалдар әдісін пайдалана отырып осы теңсіздіктердің шешімдерінің жиыны, яғни берілген 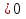 теңсіздігінің шешімдерінің жиыны (-∞;-2) мен (7;+∞) аралықтарының бірігуі болып табылатынын табамыз.
теңсіздігінің шешімдерінің жиыны (-∞;-2) мен (7;+∞) аралықтарының бірігуі болып табылатынын табамыз.
Жауабы: (-∞;-2) және (7;+∞).
Мысалы: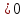
.
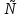
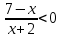
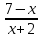
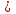
Жауабы: x 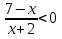 ` (-5;
` (-5; 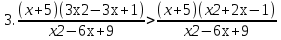 ) U (2; 3) U (3;
) U (2; 3) U (3; 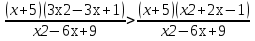 )
)
Интервалдар әдісі туралы мәселелерді оқып үйрену барысында немесе қайталау сабақтарында математикадан қабілеті бар жекелеген оқушыларға шешімі қандай да дәрежеде қиындық тудыратын төменгідей есептерді беруге болады.Бұл олардың кейбір мәселелерді қайталай отырып еңбектеніп жұмыс жасауға және жалпы математика пәні туралы,оның логикалық байланысы,тұтастығы жайлы түсініктерінің дұрыс қалыптасуына септігін тигізеді.
Сонымен қатар мұндай есептерді шығару арқылы оқушы өз білімін тереңдетеді,еңбегінің жемісін көреді.Ал ол оқушының пәнге деген қызығушылығының арттырады,қабілетін дамытады.
Сондықтан да мұғалімнің кез-келген тақырыпты өткенде қабілетті оқушылармен оларды жоғалтып алмас үшін жеке жұмыс жасауы,ол үшін өзінің де көптеген қосымша әдебиеттерді қарап шығуы,олардан керектілерін таңдап алуы яғни еңбектеніп жұмыс істеуі керек.
Қосымша есеп.Теңсіздіктерді шешіндер.
1.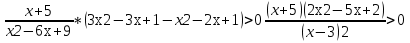
2. 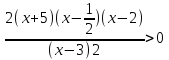 +
+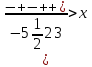
3. 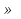
4.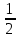
5.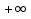
6.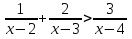
7.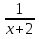
8.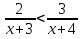
9. 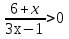
10.