Методическая разработка урока математики в 9 классе по теме «Квадратные неравенства» с применением системно - деятельностного подхода в объяснении нового материала.

Методическая разработка урока математики в 9 классе по теме «Квадратные неравенства» с применением системно - деятельностного подхода в объяснении нового материала.

Конспект урока математики в 9 классе.

Тема «Квадратные неравенства»

УМК «Алгебра: 9 класс» под ред. Г.В. Дорофеева

Учитель математики МОУ СШ № 134

Красноармейского района г. Волгограда

Сидорова Ольга Степановна

Основные дидактические цели урока:

Организовать деятельность учащихся по открытию способа решения квадратных неравенств, созданию алгоритма действий

Сформировать у учащихся навык решения квадратных неравенств по алгоритму

Структура урока:

Актуализация знаний учащихся

Мотивация

Целеполагание

Открытие способа решения квадратных неравенств

Разработка алгоритма решения квадратных неравенств

Решение неравенств по алгоритму

Итог урока (найди ошибку)

Ход урока-Здравствуйте.

Решите неравенства:

2х+7>5,

(x²+2)²< x²-4

x²-4 >0

-Здравствуйте

x>-1

х<-2

x²>4, большинство учащихся ошибочно решают неравенство, получают x>2

Мотивация

-Проверьте правильность найденного решения для числа -3

В результате проверки убеждаются, что несмотря на то, что (-3)²>2, -3>2-неверное неравенство. Понимают, что допустили ошибку. Но не понимают где.

- В чем же существенное отличие последнего неравенства от предыдущих?

-Это неравенство второй степени, наверное поэтому его не удается решить тем же способом, что линейные.

Целеполагание

-Определите тему нашего урока и его цель

-Решение квадратных неравенств.

- Научиться решать квадратные неравенства

-Какие неравенства будем называть квадратными? Определите их общий вид.

Учащиеся рассматривают разные предложения, в итоге приходят к правильному ответу: неравенства вида: ах²+bх+с>0, ах²+bх+с<0, ах²+bх+с0, ах²+bх+с0, где а отлично от нуля

Открытие способа решения квадратных неравенств

Что вы видите на доске?

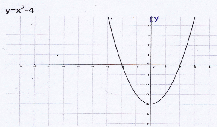
Определите направление ветвей, точки

пересечения с осью Х.

График функции у = x²-4

Ветви параболы направлены вверх, точки пересечения с осью абсцисс х=-2, х=2

-Определите по графику промежутки знакопостоянства функции.

Определяют по графику, что

у>0 при x>2, x<-2, y<0 при -2<x<-2

-Вернитесь к неравенству x²-4 >0

При каких значениях х оно справедливо?

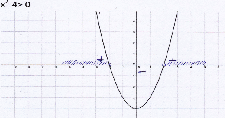
Учащиеся постепенно понимают, что у>0 при x>2, при x<-2, в то же время у = x²-4, поэтому

x²-4 >0 при x>2 и при x<-2.

-Вы решили неравенство? Дайте ответ в виде числового промежутка

Да. (-)(2; +)

-Почему число -3 является решением неравенства?

Потому что -3<-2.

-Вам помог график в решении квадратного неравенcтва?

Да.

- Решите неравенство x²-40

-Квадратные неравенства решают с помощью схемы графика. Поэтому способ называется графическим.

Записывают в тетрадях название способа.

-При решении неравенства по графику вы использовали координаты вершины параболы?

Нет

-А точки пересечения с осью Х ? Как их найти?

-Да. Решить соответствующее квадратное уравнение

-Решите неравенства с помощью схемы графика:

x²-3х<0

Учащиеся выполняют решение неравенства. Получают 0<x<3 Ответ: (0;3)

-Решите неравенства с помощью схемы графика:

- х²-2<0.

Учащиеся чертят схему графика и видят, что нет у параболы точек пересечения с осью Х. Это вызывает у большинства затруднение в нахождении решения.

-Какие значения принимает у? Что это значит?

-Только отрицательные.

Учащиеся догадываются, что ответ: ()

-Найдите все возможные способы расположения параболы относительно оси Х. Ось У не изображаем. Сколько получилось вариантов?

Учащиеся, используя шаблоны парабол делают зарисовки, чертят схемы, исследуют принципиально отличные способы расположения параболы.

В итоге приходят к выводу, что всего 6 различных вариантов расположения.

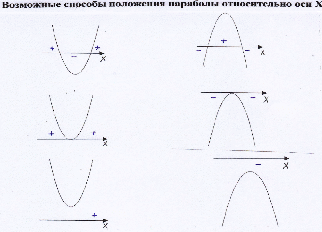
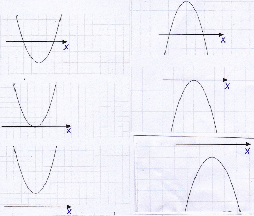
-Определите знаки «+» и «-» для каждого рисунка

Учащиеся в парах определяют знаки и у них остаются рисунки

-А теперь составьте пошаговую инструкцию для решения неравенств (алгоритм). (Фронтально, в ходе совместной работы, обсуждения составляется алгоритм).

Алгоритм проектируется на доску.

Записывают алгоритм решения квадратных неравенств:

1. Записать неравенство

2. Определить направление ветвей

3. Найти точки пересечения с осью Х (решить уравнение)

4. Изобразить схему графика

5. Расставить знаки «+» или « - »

6. Записать ответ

Решить неравенства по алгоритму:

а) х²+9<0 г) х²-6х-70

б) -x²-1>0 д) x²-6x-9<0

в) x²-4x-12<0

а) нет решений г) (-

б) нет решений д) (-)

в) (-2;6)

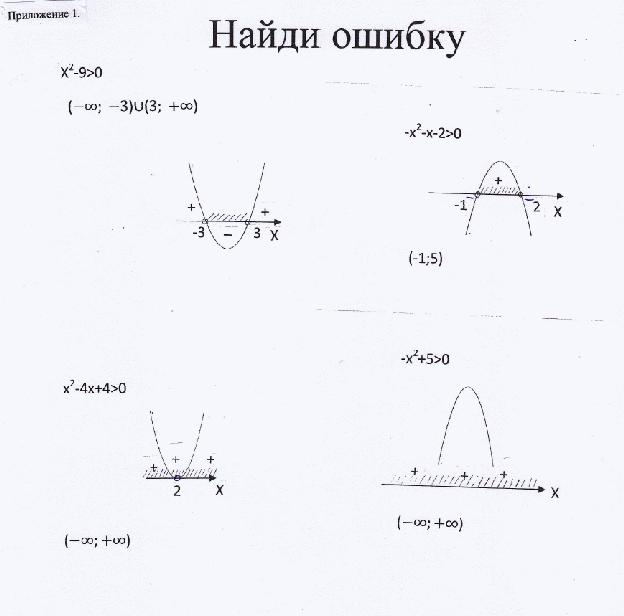
Итог урока (найди ошибку)

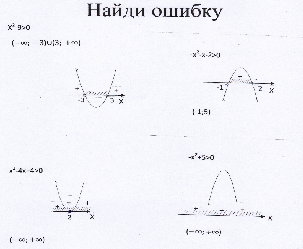
(Приложение 1).

Дети находят ошибки и говорят, что

1. В решении х²-9>0 неравенств неправильно нанесена штриховка

2. В решении неравенств -х²-х-2>0

неправильно записан ответ

3. В решении неравенства

х²-4х+4>0 точка х=2 не является

решением, поэтому ответ:

()()

4. В решении неравенства - х²+5>0

парабола при продолжении пересечет ось Х, поэтому решение неравенства: (-).

Домашнее задание

Пункт 2.5, № 294, 301 (а,б)

Резюме.

В ходе урока был использован системно-деятельностный подход. На каждом этапе урока была мотивация учащихся. Вопросы учителя выстроены в системе, большинство вопросов анализа и синтеза. Учащиеся строили гипотезы решения квадратных неравенств, открывали способ решения неравенств. Составляли алгоритм решения и решали неравенства по алгоритму. Задания для учащихся намеренно не насыщены сложными вычислениями, чтобы отработать главное: способ решения квадратных неравенств. В целях подведения итога урока и осуществления рефлексии учащиеся исправляли ошибки в решении неравенств, спроектированных на доску.

Методическими особенностями данного урока являются:

- структура заданий, подводящих учащихся к открытию способа решения неравенств;

- установление учащимися причинно-следственных связей на каждом этапе урока;

- практическая работа по исследованию возможных способов расположения параболы относительно оси Х;

- поиск ошибок и их исправление .

5