- Учителю
- Олимпиадная работа по математике 7 класс
Олимпиадная работа по математике 7 класс
Олимпиадная работа по математике 7 класс.
-
Решите следующий числовой ребус:
Ответ: 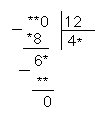
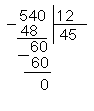
2. В трёх коробках лежат 180 карандашей. Известно, что во второй коробке их в 2 раза больше, чем в первой, а в третьей - в 3 раза больше, чем во второй. Сколько карандашей во второй коробке?
Ответ: 40 карандашей
3. Сколько имеется четырехзначных чисел, которые делятся на 45, а две средние цифры у них - 97?
Ответ: Два числа: 6975, 2970
Решение: Число делится на 45, следовательно, оно делится на 5 и на 9. Раз число делится на 5, то последняя цифра записи числа 0 или 5 .Получим числа вида *970 или *975. Раз число делится на 9, то сумма его цифр делится на 9.
9+7+0=16 первая цифра 2, число 2970
9+7+5=21 первая цифра 6, число 6975.
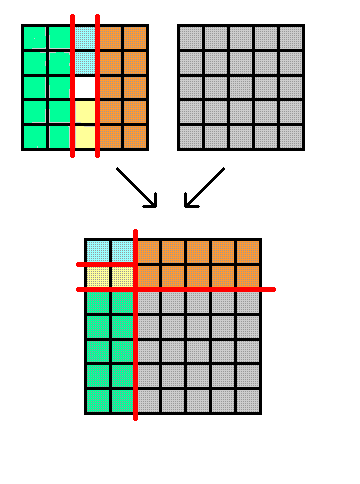
4. Разрежьте квадрат с дыркой двумя прямыми на 4 части так, чтобы из них и еще одного обычного квадрата 5×5 можно было сложить новый квадрат.
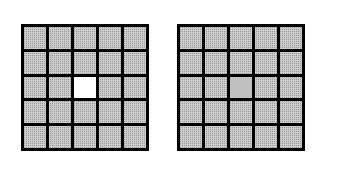
Ответ:
5. Как-то три учителя на практикуме решили продемонстрировать ученикам свое умение размышлять. Они взяли 5 шляп (если кто-то не может представить древнегреческих учителей в шляпах, пусть представит их в разноцветных венках или повязках на голове) - 3 белые и 2 черные - и попросили одного из учеников надеть каждому из них по шляпе. Ученик мог выбрать каждому произвольный цвет шляпы и надеть ее так, чтобы ни один мудрец не видел цвет своей шляпы. Ученик надел каждому по белой шляпе, решив, что так сделает выбор учителей труднее. Учителя договорились о том, что, если кто-либо из них догадается, какого цвета у него шляпа, он сразу же должен заявить об этом. Вскоре один из них догадался, что у него белая шляпа.
а) Как он рассуждал?
б) Действительно ли ученик выбрал для мудрецов самый трудный вариант?
Ответ:
а) Пусть первым догадался мудрец А. Он мог рассуждать следующим образом: «Предположим, что у меня шляпа черная. Тогда Б видит мою черную шляпу и белую шляпу В и думает, какого цвета его шляпа. «Если бы моя (Б) шляпа была черной, то В, видя 2 черные шляпы, сразу же заявил бы о белом цвете своей шляпы». Однако В молчит. Следовательно, Б должен сделать вывод о том, что его шляпа не черная, а белая, и заявить об этом. Однако и Б молчит. Следовательно, мое исходное предположение о том, что у меня шляпа черная, ложно. Таким образом, у меня шляпа белая.
б) Если у одного мудреца, например Б, черная шляпа, то А, предположив, что и у него шляпа тоже черная, ожидал бы, что В сразу же догадается, что у него белая шляпа, так как черных шляпы всего 2. Следовательно, А еще быстрее догадался бы о цвете своей шляпы, чем в случае, когда у всех белые шляпы.
Если же у двух мудрецов черные шляпы, а у третьего белая, то он моментально об этом догадался бы.