- Учителю
- Разработка урока и презентация по теме 'Формулы тригонометрических функций двойного угла ' (9 класс)
Разработка урока и презентация по теме 'Формулы тригонометрических функций двойного угла ' (9 класс)
Тема урока: Формулы тригонометрических функций двойного угла
Цели урока: 1. Изучить вывод формул двойного угла, показать их применение, развить
умение использовать эти формулы в тригонометрических преобразованиях;
2. Вырабатывать навыки и умения использовать полученные формулы в
тригонометрических преобразованиях, развивать математическое
мышление учащихся, умение видеть и применить изученные тождества
3. Воспитание информационной культуры, интереса к математике, воспитание
отзывчивости, трудолюбия, аккуратности.
Тип урока: Урок ознакомления с новым материалом. Оборудование и наглядность: Компьютер, интерактивная доска, презентация для сопровождения урока, схема с формулами синуса и косинуса двойного угла, жетоны, карточки с самостоятельной работой.
Ожидаемый результат: Каждый учащийся должен знать вывод формул двойного аргумента и уметь применять их для преобразований тригонометрических выражений на уровне обязательных результатов обучения.
ХОД УРОКА:
I. Организация начала урока:
а) Взаимное приветствие;
б) отметить отсутствующих;
в) проверить готовность к уроку;
г) постановка цели урока:
Сегодня на уроке мы изучим новые формулы тригонометрии - формулы двойного аргумента и рассмотрим многообразие их применения.
Эпиграфом нашего урока будут слова Бернардо Больцано "Формула подчас кажется более мудрой, чем выдумавший ее человек" (слайд 2).
II. Повторение изученного материала:
-
Мотивационный момент
Ребята, обратите внимание на следующие слова: (слайд 3)
«В сфере высшего образование должна быть проведена оптимизация сети ВУЗов с уделением особого внимания на техническое образование»
Н. А. Назарбаев
«Мы должны быть готовы к острой конкуренции»
Н. А. Назарбаев
Итак, перед вами поставлена задача - быть конкурентноспособными в
своих математических знаниях, так как государство взяло курс на
технический прогресс, а математика, как известно, его составляющая.
-
Тестирование учащихся с помощью компьютера (ноутбука), с использованием программы Microsoft Excel: формулы сложения
Тест по теме «Формулы сложения»
-
сos (х + у) =
1) cos х cos у + sin х sin у; 2) cos х cos у - sin х sin у;
3) cos х sin у - sin х cos у; 4) cos х sin у + sin х cos у;
2. tg (x - y) =
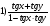
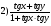
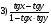
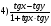
3. sin 5х cos 3х + sin 3х cos 5х =
1) sin 2x 2) cos 2x 3) sin 8x 4) cos 8x
4. cos 180 cos 120 - sin 180 sin 120 =
1) 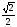 2)
2) 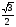 3) 0,5 4) 0
3) 0,5 4) 0
5. cos 1070 cos 170 + sin 1070 sin 170 =
1) 0 2) 1 3) - 1 4) 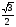
6. sin 170 cos 130 + sin 130 cos 170 =
1) 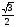 2) 0 3) - 0,5 4) 0,5
2) 0 3) - 0,5 4) 0,5
7. 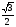
1) 1 2) 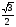 3)
3) 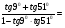 4)
4) 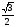
8. cos(α + β), если α = 420, β = 180
1) - 0,5 2) 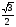 3) 0,5 4)
3) 0,5 4) 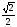
9. sin 4х cos х - sin 2х cos 4х;
1) sin 2x 2) cos 2x 3) sin 6x 4) cos 6x
10. 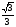
1) tg 8x 2) ctg 2x 3) ctg 8x 4) tg 2x
Ответы:
-
1
2
3
4
5
6
7
8
9
10
2
4
3
2
1
4
4
3
1
4
-
Устные упражнения: (Устные упражнения проводятся одновременно с тестированием сильных учащихся)
-
Вспомним формулу синус суммы, косинус суммы и тангенс суммы аргументов.
Вспомним формулу синус разности, косинус разности и тангенс разности аргументов
Вызываются 2 ученика, которые на 2 досках записывают отдельно эти формулы:
(формулы суммы тригонометрических функций, записанные на интерактивной доске сохранить для дальнейшего изучения темы урока)
на интерактивной доске на обычной доске
sin(α + β) = sin α cos β + cos α sin β; sin(α - β) = sin α cos β - cos α sin β;
cos(α + β) = cos α cos β - sin α sin β; cos(α - β) = cos α cos β + sin α sin β;
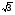
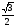
-
Далее учащиеся устно работают с места (слайды)
№ 1. Упростить: (слайд 4)
а) cos α cos 3α - sinα sin3α
б) sin 2α cos α + cos 2α sin α
в) sin α cos 3α + cos α sin 3α
г) 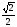
№ 2. Вычислить: (слайд 5)
а) sin 100 cos 200 + cos 100 sin 200
б) cos 140 cos 160 - sin140 sin160
в) sin 300 cos 150 + cos 300 sin 150
г) cos 170 cos 280 - sin170 sin 280
д) 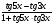
III. Изучение нового материала.
-
Сейчас мы выведем с вами тригонометрические формулы двойного аргумента и рассмотрим многообразие их применения. Каждую из 3-х формул выводит 1 ученик.
Если положить в формулах, записанных вами в начале урока на доске x = y, то получаем:
-
sin(α + β) = sin α cos β + cos α sin β
sin 2α = sin α cos α + sin α cos α = 2sin α cos α sin 2α = 2sinα cosα (слайд 7)
-
cos(α + β) = cos α cos β - sin α sin β
cos 2α = cos α cos α - sin α sin α = cos2 α - sin2 α cos 2α = cos2 α - sin2 α (слайд 6)
3) 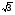
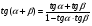
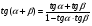 (слайд 8)
(слайд 8)
-
Просмотр слайдов (одновременно)
-
Показать применение данных формул (слайды 9, 10).
-
Упростить выражение:
А) 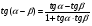
Б) 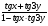
В)
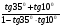
-
Физминутка
IV. Закрепление изученного материала:
-
Привести примеры на применение формул двойного угла из текста учебника с. 132:
Пример 1: Упростите выражение: 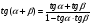
Пример 2: Вычислим значение sin 2α, зная, что sin α = 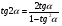 и 0 ˂ α ˂
и 0 ˂ α ˂ 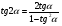
-
Тригонометрия в стихах - самостоятельное домашнее задание, данное на предыдущем уроке учащимся;
-
Работа с учебником: № 364 (в, г, е), 366 (а, б)
-
Самостоятельная работа по карточкам
Учащиеся выполняют работу на карточках с дифференцированными заданиями по теме урока (самопроверка).
1 вариант.
№1. Упростите, продолжив решение, и выберите правильный ответ:
а) 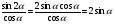
Ответ: 1) 4/3; 2) 4/3cos x; 3) 2/3; 4) 4/3ctg x.
б) 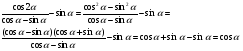
Ответ: 1) cos 20; 2) 2cos 20; 3) ctg 20; 4) другой ответ.
№2. Упростите и выберите правильный ответ:
а) 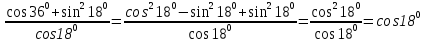
Ответ: 1) 3tg x; 2) 3sin x; 3) 1,5 sin x; 4) 3tg 2x.
б) cos2t - cos2t =
Ответ: 1) sin2t; 2) - sin2 t; 3) 2cos2 t + sin2 t; 4) другой ответ.
2 вариант.
№1. Упростите, продолжив решение, и выберите правильный ответ:
а) 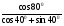
Ответ: 1) -3tg 2x; 2) 3sin 2 x; 3) 6 tg x; 4) 3tg 2 x.
б) 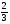
Ответ: 1) 3/2; 2) 2/3; 3) 2/3sin 2x; 4) другой ответ.
№2. Упростите и выберите правильный ответ:
а) 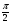
Ответ: 1) tg 2x; 2) 2sin x; 3) 1/2sin x; 4) 1/2 + tg x.
б) cos2t + sin2t =
Ответ: 1) cos2 t; 2) 2sin t; 3) cos t - sin t; 4) другой ответ.
Проверяются верные ответы.
1 вариант: №1 а) 1; б) 2. №2 а) 2;б) 1.
2 вариант: №1 а) 4; б) 2. №2 а) 3; б) 1.
V. Итоги урока:
1. д / з: § 23 (формулы двойного угла), № 367
2. Оценки за урок