Карта изучения темы «Функции» УМК М. И. Башмаков «Математика для НПО и СПО», М: Академия,2013

Карта изучения темы «Функции» УМК М. И. Башмаков «Математика для НПО и СПО», М: Академия,2013₁: Определять по формуле простейшей зависимости вид ее графика.

ПЦ₂: Уметь вычислять значение функции по заданному значению аргумента при различных способах задания функции.

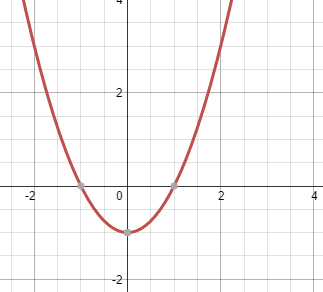
Заполнитe таблицу:

5

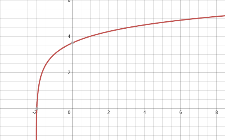
-1; 1

Задания с пропусками:

1. Отметить правильное определение функции:

а) Функцией у = f(х) называется такая зависимость переменной у от переменной х, при которой каждому значению переменной х соответствует одно и только одно значение переменной у.

б) Функцией у = f(х) называется такая зависимость переменной у от переменной х, при которой одному значению переменной х соответствует не менее одного значения переменной у.

в) Функцией у = f(х) называется такая зависимость переменной у от переменной х, при которой некоторым значениям переменной х соответствует хотя бы одно значение переменной у.

2. Завершить высказывания.

Для функции p = f(x), все значения независимой переменной _____образуют______________________

Для функции p = f(x), все значения зависимой переменной _____образуют______________________

3. Завершить определение:

Функция называется возрастающей в некотором промежутке, если для любых двух значении аргумента из этого промежутка большему значению аргумента соответствует______________

ПЦ₁: Знать основные свойства числовых функций

ПЦ₂: Определять основные свойства числовых функций, заданных символически, словесно, графически

ПЦ₃: Уметь строить графики изученных функций, иллюстрировать по графику их свойства

ПЦ₄: Приводить примеры функциональных зависимостей в реальных процессах и явлениях

Построить эскиз графика функции по заданным свойствам.

1 вариант

2 вариант

Область определения.

[-6; 7]

[-5; 7]

Область значений.

[-5; 3]

[-2; 6]

Нули:

Промежутки знакопостоянства:

а) f (x) > 0;

б) f (x) < 0.

(-4;-1)

[ -6; -4), (-1; 7]

[-5; -3), (-1;7]

(-3;-1)

Промежутки:

а)возрастания;

б) убывания.

[-6; -2], [1; 4]

[-2; 1], [ 4; 7]

[-2; 2], [5; 7]

[-5; -2], [2; 5]

Точки максимума.

Максимум функции.

-2; 4

f (-2) = 3, f (4) = -1

2

f (2) = 4

Точки минимума.

Минимум функции.

1

f (1) = -4

-2;5

f (-2) = -2; f (5) = 1

Дополнительные точки

графика.

f (-6) = -4;

f (7) = -5

f (-5) = 4;

f (7) = 6

ПЦ₁: Изучить понятие обратной функции, определять вид и строить график обратной функции, находить ее область определения и область значений.

ПЦ₂: Изучить понятие композиции функции, определять вид и строить график композиции функций, находить ее область определения и область значений.

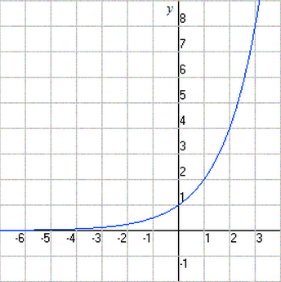
Дан график функции. Построить в этой же системе координат график обратной функции. Сформулируйте необходимое условие существования обратной функции.

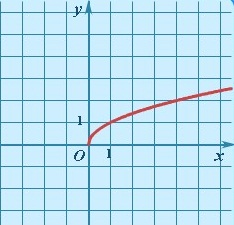
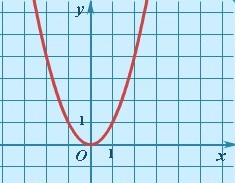
ПЦ₁: Знать и уметь выполнять преобразования графика функции

ПЦ₂: Использовать понятие функции для описания и анализа зависимостей величин, представлять их графически и интерпретировать графики

ПЦ₃: Составлять функции по данному условию, решать задачи на экстремум, наибольшее(наименьшее) значения.

ПЦ₄: Знать особенности функций: точки разрыва, угловые точки, выпуклости функции, асимптоты графика.

КР:

1. Постройте график функции у=х²-4х+3 и укажите ее свойства.

2. Дан график функции y=f(x). Постройте графики функций: y=f(x-1); y=f(x)+1; y=f(2x).

3. Для функции y= найдите обратную; постройте график данной функции и обратной к ней; для каждой из них укажите область определения и множество значений.

4. Дана функция . Составьте формулу функции и найдите ее значение при х=5.

5. На графике изображена зависимость скорости движения рейсового автобуса от времени. На вертикальной оси отмечена скорость автобуса в км/ч,
   
   на горизонтальной - время в минутах, прошедшее с начала движения автобуса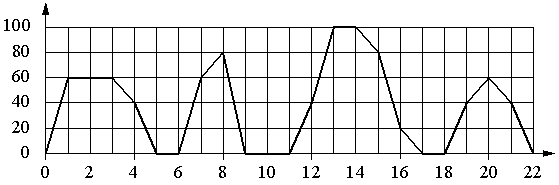

Пользуясь графиком, поставьте в соответствие каждому интервалу времени характеристику движения автобуса на этом интервале.

ИНТЕРВАЛЫ ВРЕМЕНИ

А) 4-8 мин.Б) 8-12 мин.В) 12-16 мин.Г) 18-22 мин.

ХАРАКТЕРИСТИКИ

1) была остановка длительностью 2 минуты

2) скорость не меньше 20 км/ч на всём интервале

3) скорость не больше 60 км/ч

4) была остановка длительностью ровно 1 минута

Задания для внеаудиторной самостоятельной работы

Инструкция по выполнению:

1. Внимательно изучите задание.

2. Подберите компьютерную программу (графический калькулятор) для выполнения задания.

3. Выполните задание в программе, сохраните скриншот.

4. Вывод сделайте сразу же после выполнения задания.

5. Убедиться в правильности сделанного вывода на контрольных примерах.

6. Запишите вывод в тетрадь.

Задание 1.

1. Постройте последовательно разными цветами графики функций у=sinx, у=2sinx, у=0,5sinx.

2. Выявите связь между получившимися графиками.

3. Проверьте свои выводы для функций у=4sinx, у=0,3sinx.

4. Заполните пропуски в предложениях и запишите их в тетрадь:

График функции у=кsinx при к>1 получается из графика функции у=sinx путем …………… вдоль оси ОУ. График функции у=кsinx при 0<к<1 получается из графика функции у=sinx путем …………… вдоль оси ОУ.

Задание 2.

1. Постройте последовательно разными цветами графики функций у=sinx, у=sin2x, у=sin0,5x.

2. Выявите связь между получившимися графиками.

3. Проверьте свои выводы для функций у=sin3x, у=sinx/4.

4. Заполните пропуски в предложениях и запишите их в тетрадь:

График функции у=sinmx при m>1 получается из графика функции у=sinx путем …………… вдоль оси ОХ. График функции у=sinmx при 0

Задание 3.

1. Постройте последовательно разными цветами графики функций у=sinx, у=sinx+2, у=sinx-3.

2. Выявите связь между получившимися графиками.

3. Проверьте свои выводы для функций у=sinx+1, у=sinx-2.

4. Заполните пропуски в предложениях и запишите их в тетрадь:

График функции у=sinx+n при n>0 получается из графика функции у=sinx путем …………… вдоль оси ОУ. График функции у=sinx+n при n<0 получается из графика функции у=sinx путем …………… вдоль оси ОУ.