Методические рекомендации по теме Модуль

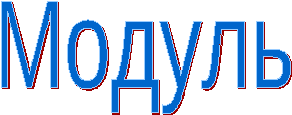
Выполнили учащиеся 9 Б класса

МОУ «Средняя общеобразовательная школа №1»

г. Курска

20013-2014 уч. год

1. Понятие модуля.

Модулем действительного числа (абсолютной величиной числа х) называют само это число, если х ≥ 0, и противоположное число, если х < 0.

Т.е.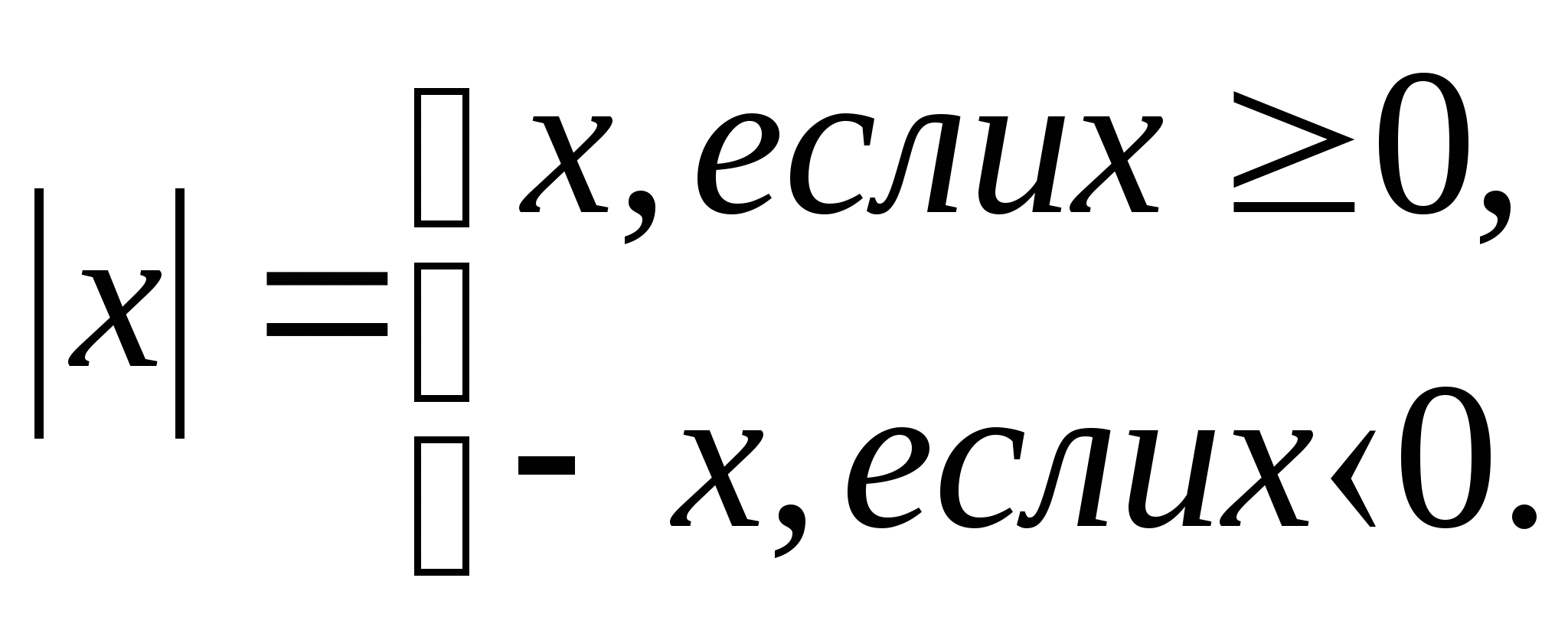

Геометрически означает расстояние на координатной прямой от точки х до 0.

Расстояние между точками х и b координатной прямой равно , т.е. =

Пример 1.

Расстояние между точками х и 1 на координатной прямой равно 2. Этими точками являются х₁ = 3, х₂ = -1.

Ответ: 3;-1

Пример 2. > 2

Расстояние между точками х и 1 больше 2, т. е.

Ответ:

Пример 3. ≤ 2

Расстояние между точками х и 1 не больше 2., т.е

Ответ:

Таким же образом можно решать и более сложные уравнения:

,

Например:

Решить данное уравнение, значит найти все такие точки на координатной прямой, для каждой из которых сумма расстояний от её до точек с координатами 1 и 3 равна 6. Ясно, что ни одна из точек отрезка [1;3] не удовлетворяет этому условию, так как сумма указанных расстояний для любой из них равна 2 (т.е. не равна 6). Вне этого отрезка существует только две искомые точки.

Точка с координатой 5 и точка с координатой -1. Это и есть решение данного уравнения.

Ответ: 5;-1.

Свойства:

1. Модуль любого числа - неотрицательное число.

2. Модули противоположных чисел равны.

3. Величина числа не превосходит величины его модуля.

4. Модуль произведения равен произведению модулей сомножителей.

5. 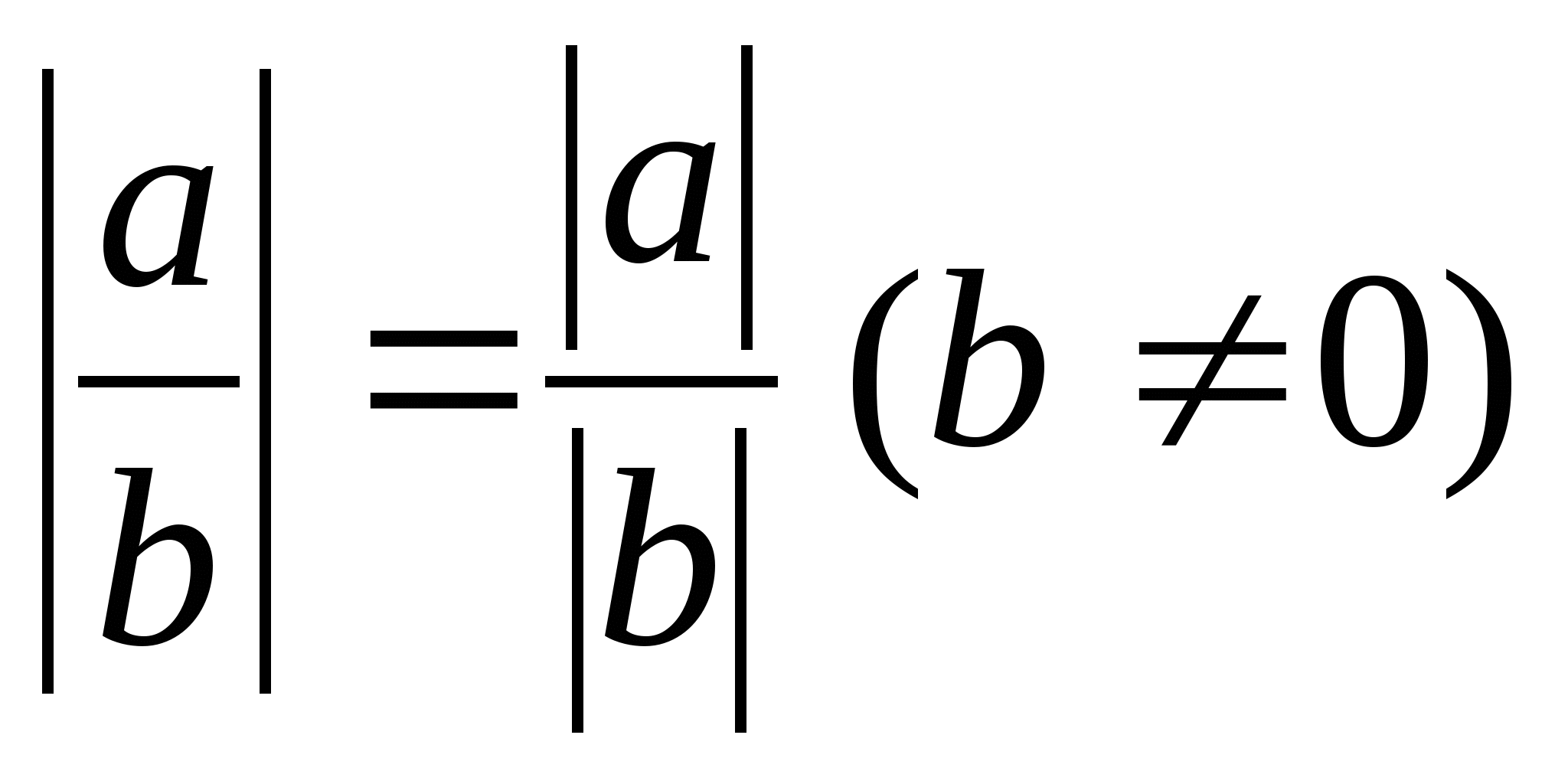Модуль дроби равен модулю числителя, делённому на модуль знаменателя (если модуль знаменателя не равен нулю)

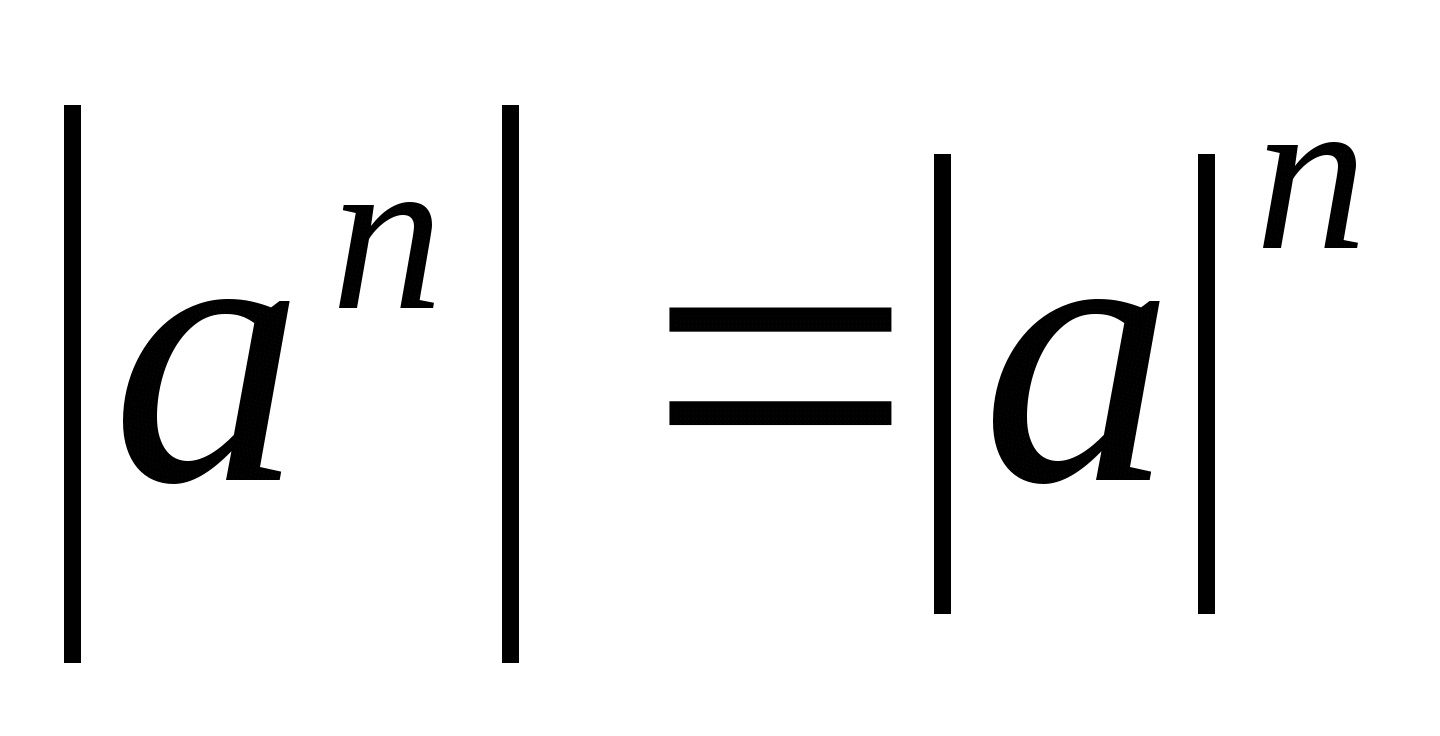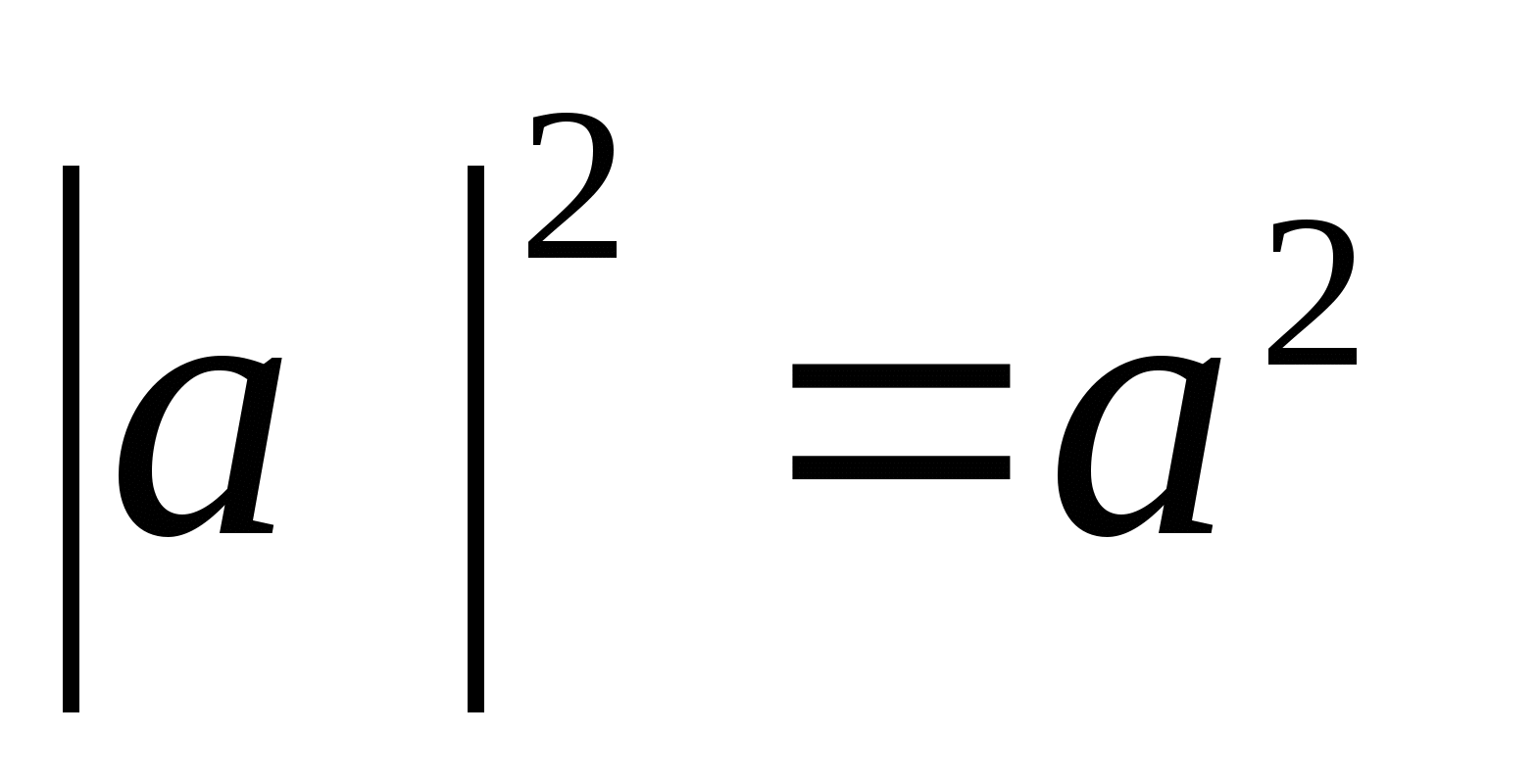6. 7. 8.

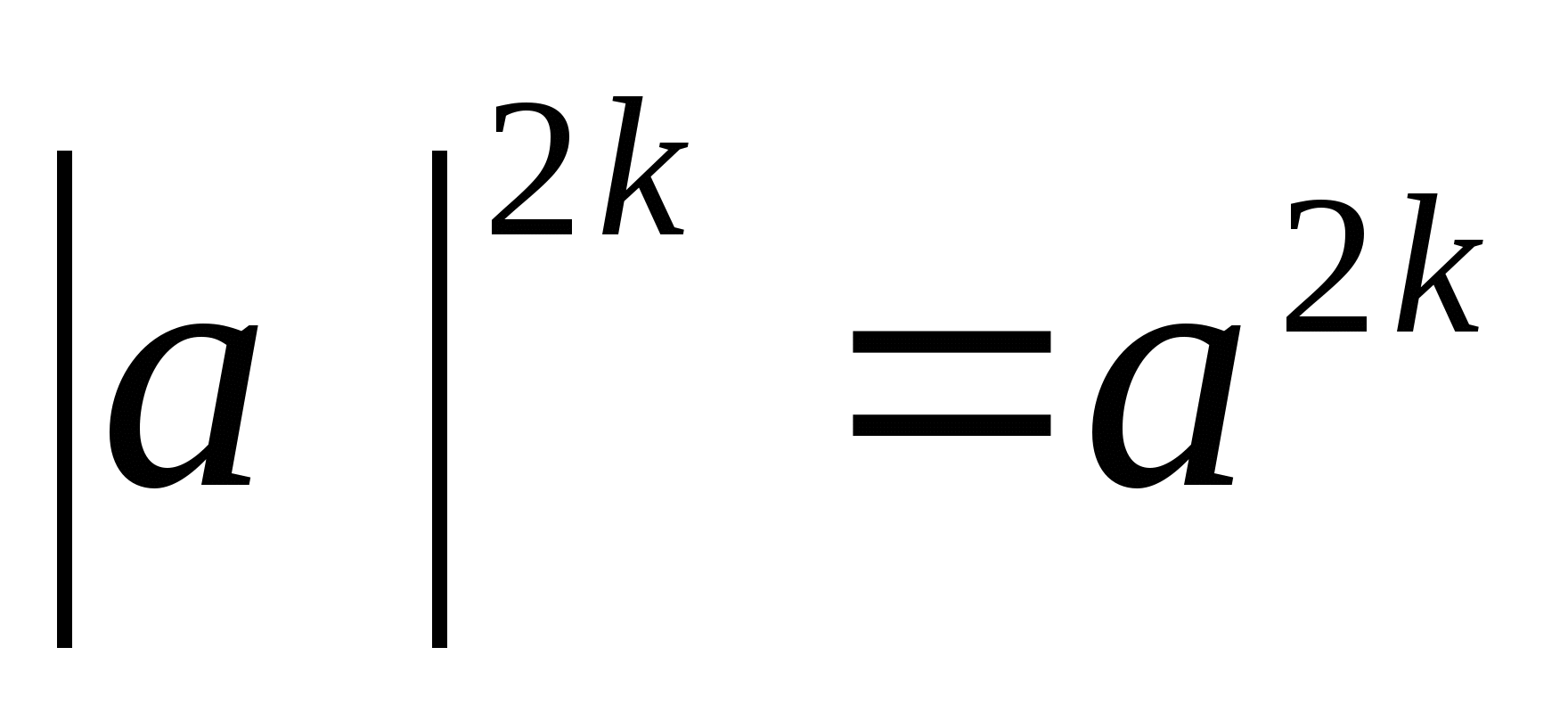
9. Модуль суммы не превосходит суммы модулей слагаемых.

10.

2. Уравнения, содержащие переменную под знаком модуля.

В своём проекте мы рассматриваем методы решения уравнений, содержащих переменную под знаком модуля. Чтобы решить такие уравнения, надо освободиться от знака модуля. Рассмотрим несколько случаев.

а)

Если:

а < 0 , то данное уравнение не имеет корней;

а = 0, то данное уравнение равносильно уравнению f(x) = 0;

a > 0, то

или

Решить уравнение:

х² - 2х - 7 = 4 или х² - 2х - 7 = - 4

х² - 2х - 11 = 0 х² - 2х - 3 = 0

х_1,2 = х₃ = -1; х₄ = 3.

Ответ: ; - 1; 3.

б)

Решением является объединение решений двух систем:

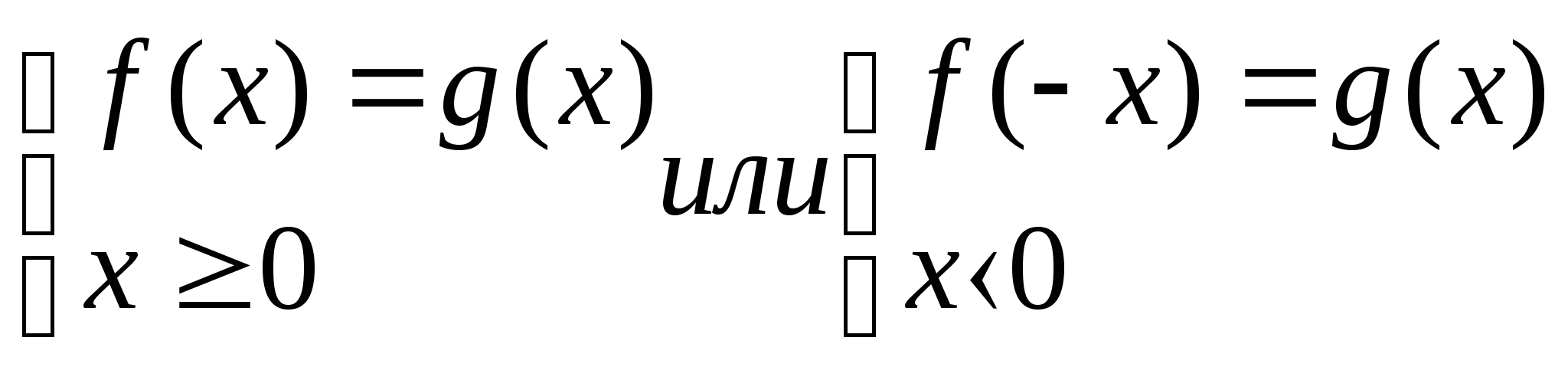
Решить уравнение:

1 способ

Используя определение модуля имеем

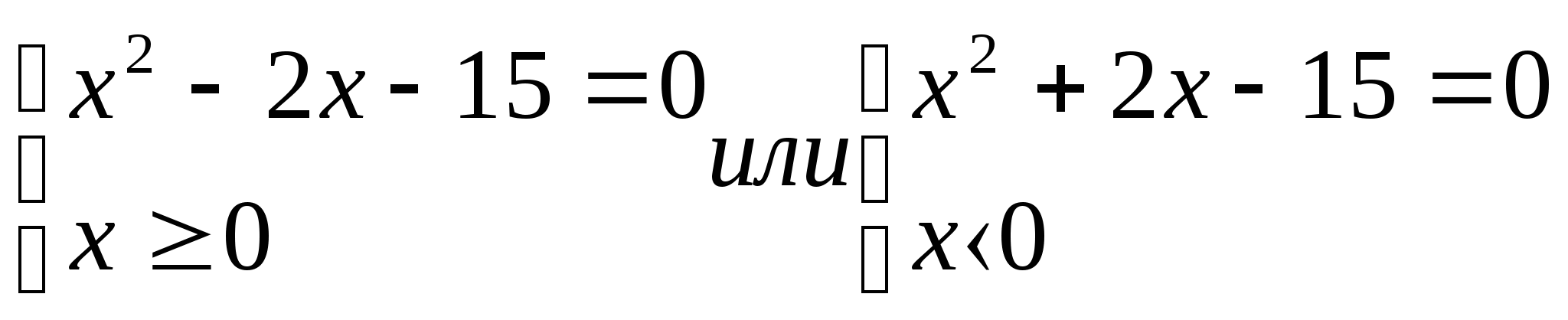
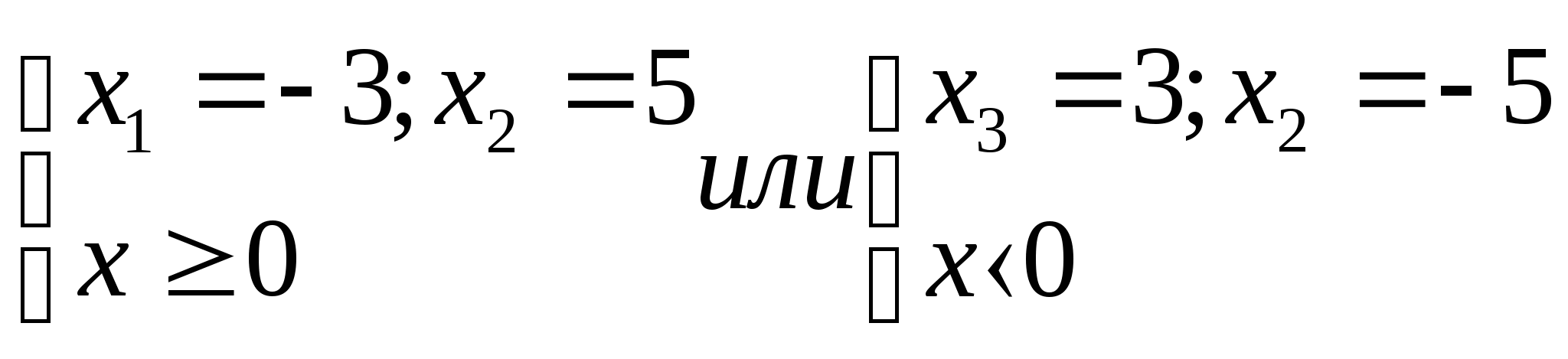
х= ± 5.

Ответ: ± 5.

2 способ Данное уравнение можно решить, используя метод замены переменой. Пусть = у, тогда данное уравнение примет вид: у² - 2у - 15 = 0 (т.к. х² = ²) Решая его , получаем корни у₁= - 3; у₂ = 5.Возвращаясь к замене, получим = -3 или = 5. первое уравнение корней не имеет, а второе имеет два корня -5 и 5.

Ответ: ±5.

в)

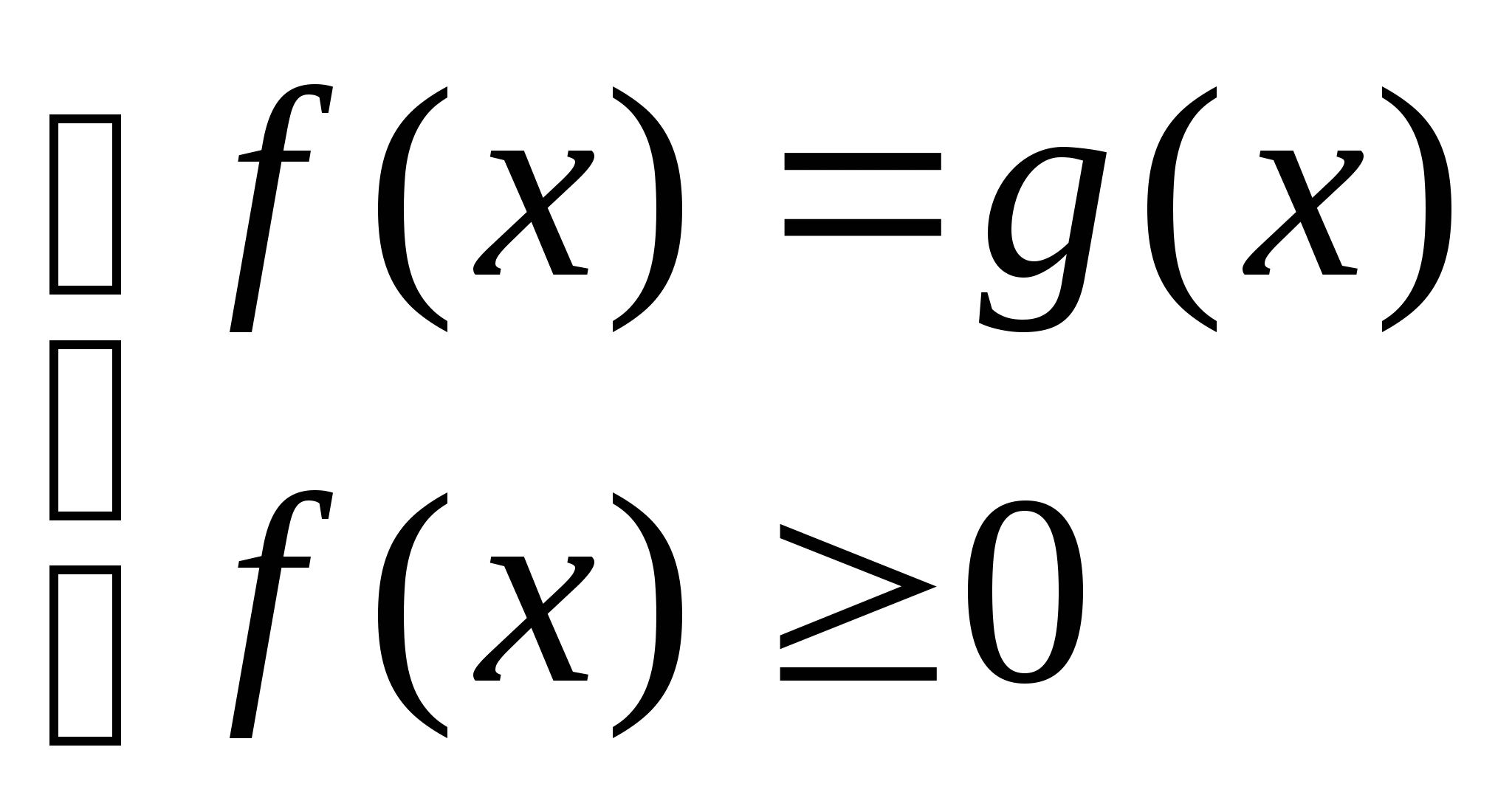или

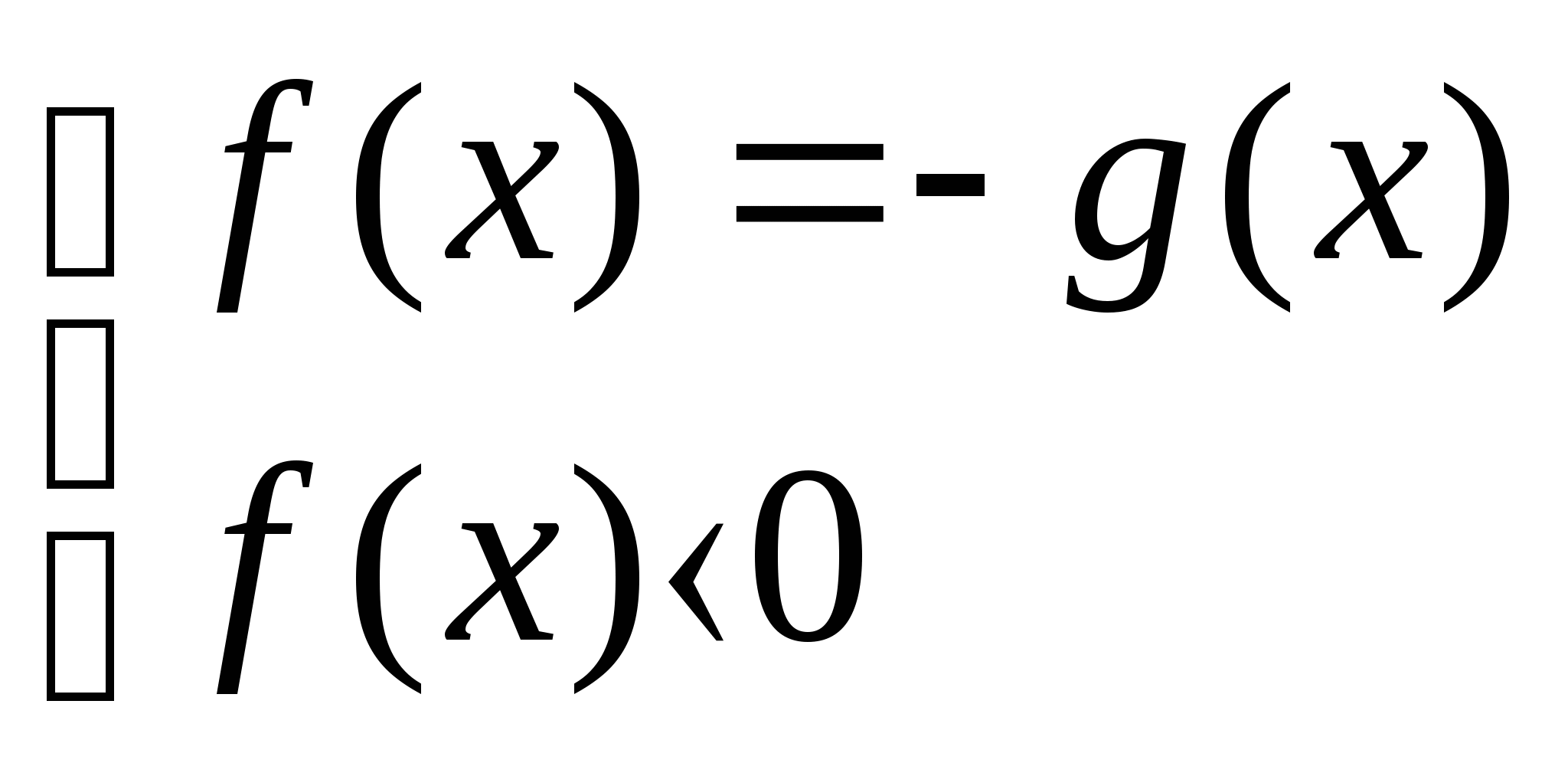
Решить уравнение

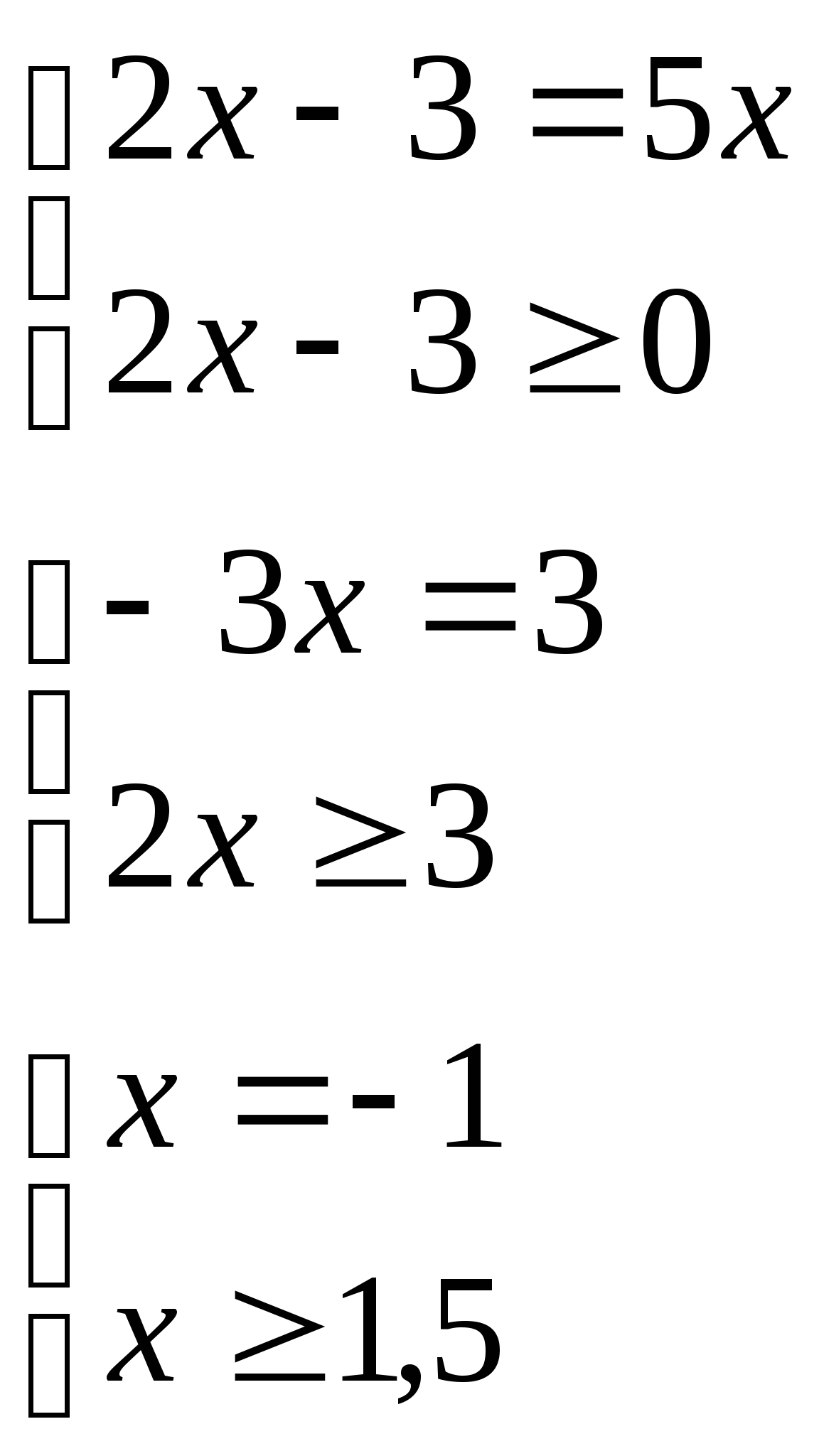или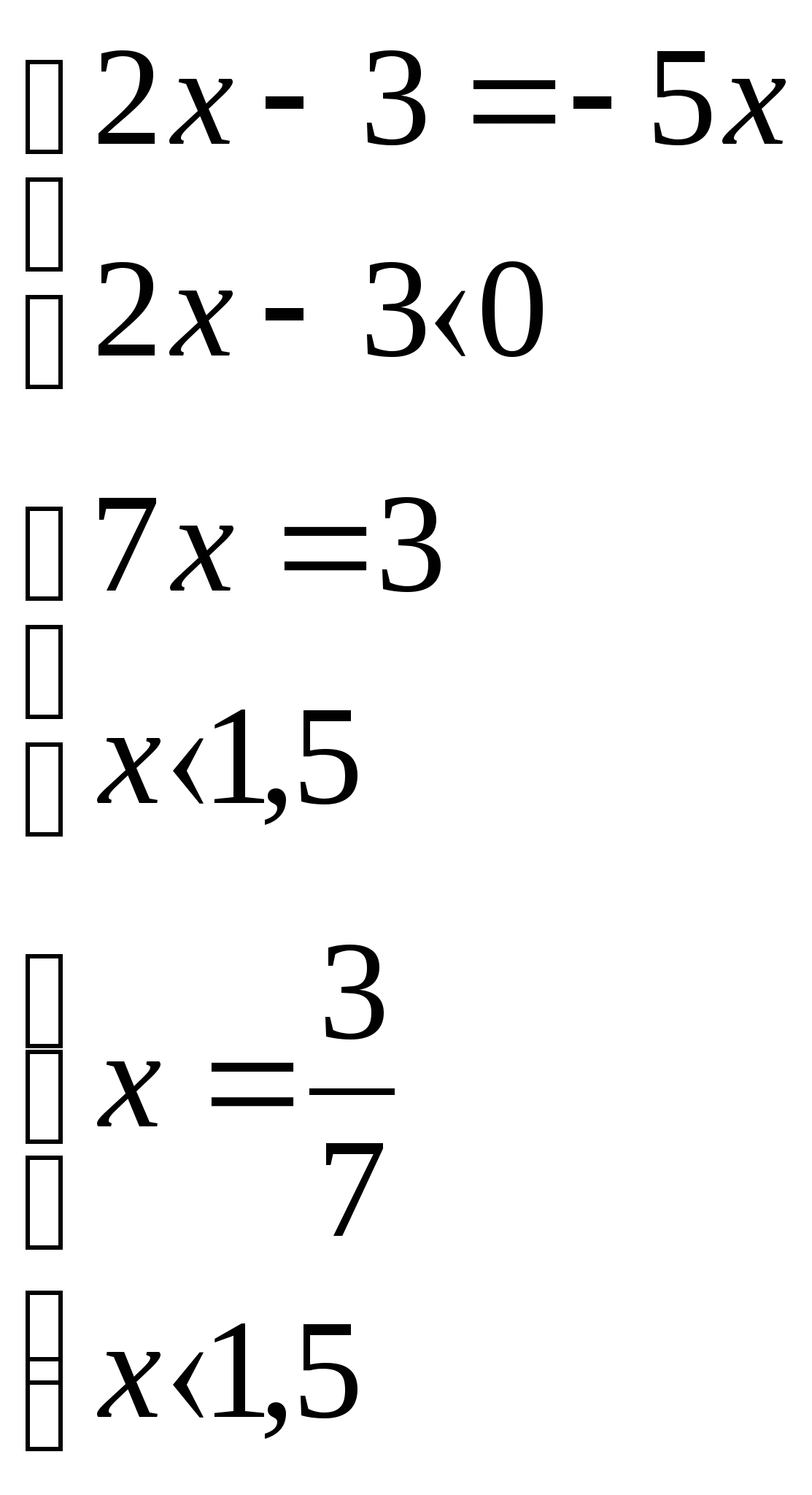

Ответ:.

г) Для решения ряда уравнений с модулем можно воспользоваться утверждением. Два числа, модули которых равны, либо равны между собой, либо отличаются знаком, т.е. если

Решить уравнение:

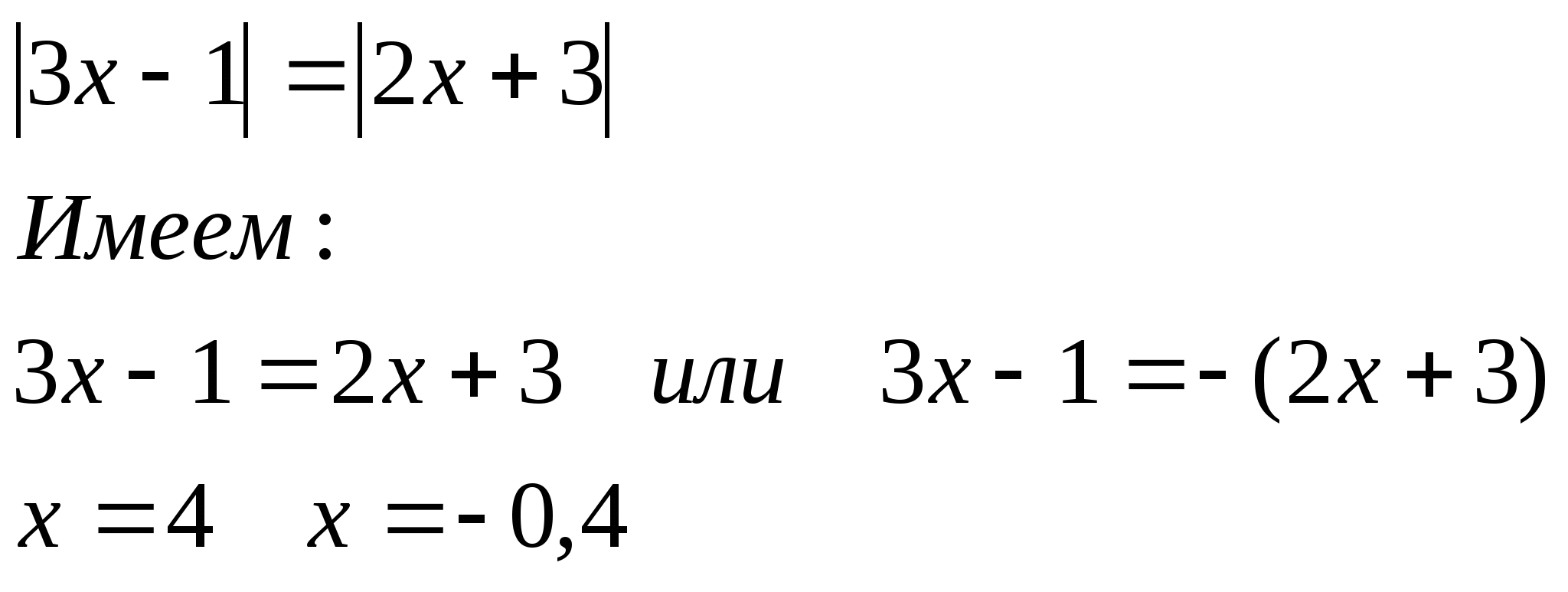
Ответ:4; -0,4.

д) Решите уравнение:

Анализируя данное уравнение, видим, что левая часть представляет сумму двух неотрицательных величин, поэтому равенство нулю возможно тогда и только тогда, когда оба слагаемых одновременно равны нулю, т.е. данное уравнение равносильно системе:

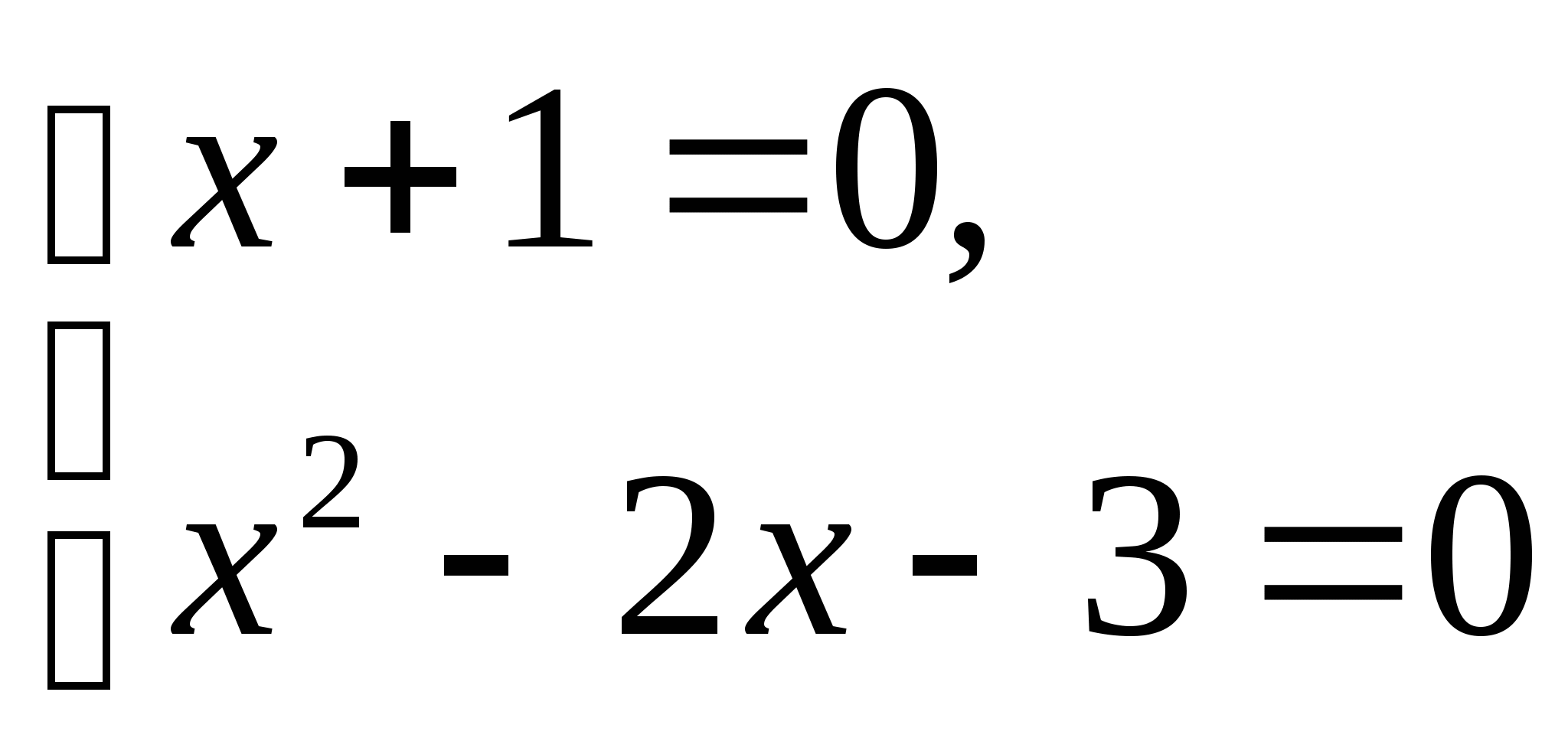
Решив первое (оно проще) проверим, будет ли число -1 являться корнем второго уравнения.

Ответ: -1.

3. Неравенства, содержащие переменную под знаком модуля

а), где а > 0 равносильно двойному неравенству -а ≤ f(x) ≤ а,

если а = 0 , то равносильно уравнению f(a) = 0.

Пример:

-2< х-1 < 2

-2 +1 < х < 2+1

-1 < х < 3.

Ответ:( -1;3)

б) , где а ≥ 0 равносильно неравенствам:

f(x) ≥ a или f(x) ≤ -a

Пример:

2х + 5 ≥ 7 или 2х + 5 ≤ -7

2х ≥ 2 2х ≤ - 12

х ≥ 1 х ≤ -6

Ответ:

4. Построение графиков функций, содержащих знаки модуля.

а)

Для построения графика данной функции необходимо изобразить график функции у = f(x) после чего часть графика, лежащую выше оси абсцисс и на ней, оставить неизменной, а часть графика, лежащую ниже этой оси, заменить ее образом при симметрии относительно оси абсцисс.

б)

Для построения графика данной функции надо взять часть графика функции у = f(x), лежащую в полуплоскости х ≥ 0, симметрично отобразить её относительно оси у и объединить получившиеся множества.

в)

Для построения данного графика достаточно применить алгоритм построения графика функции , а потом функции , или наоборот.

г)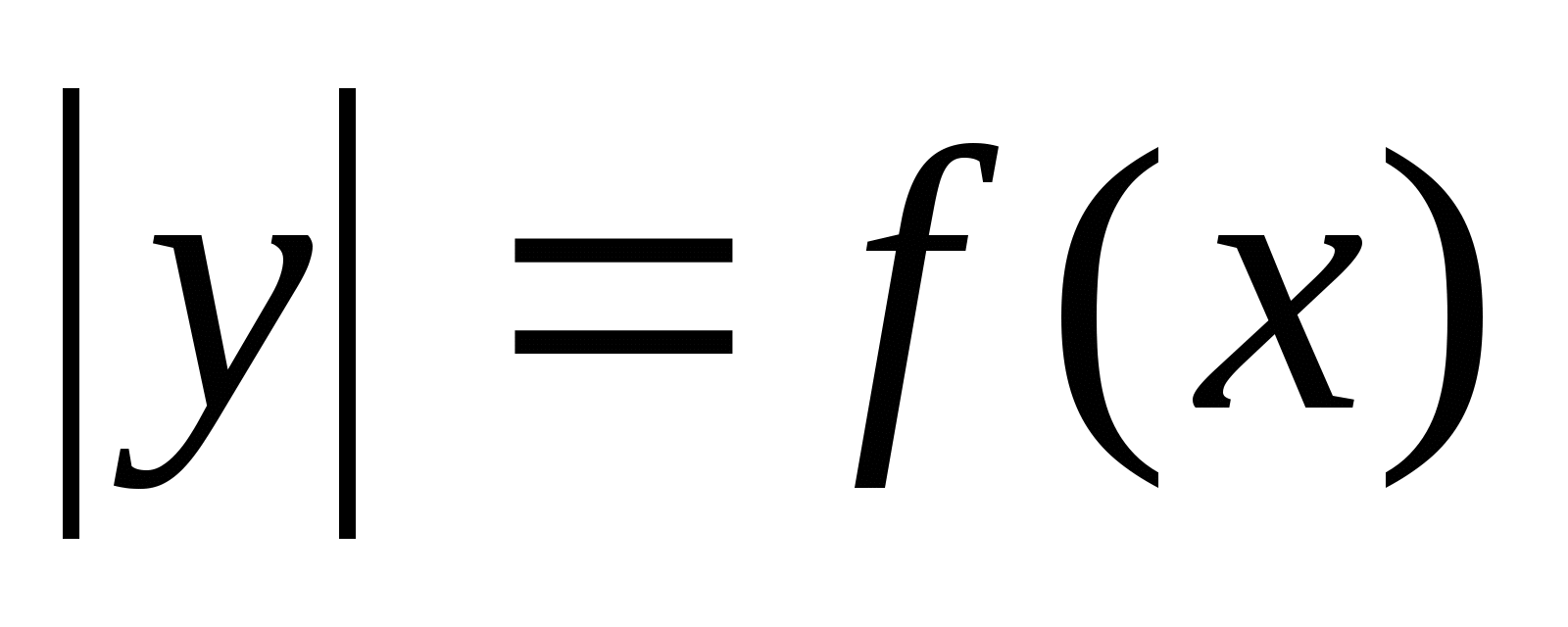

Для построения графика данного уравнения необходимо ту часть графика уравнения у = f(x) , которая лежит выше оси абсцисс и на ней симметрично отобразить относительно оси х и объединить получившиеся множества. Данную зависимость между переменными х и у, выраженную данным равенством нельзя отнести к функциональной. Именно в таких случаях надо говорить об уравнении, а не о функциях.

Задания для работы

Решить уравнения, используя геометрическое определение модуля

1.

2.

3.

4.

Решить уравнения

1.

2.

3.

4.

5.

Решить неравенства

1.

2.

3.

4.

Построить графики уравнений, содержащих переменную под знаком модуля

1.

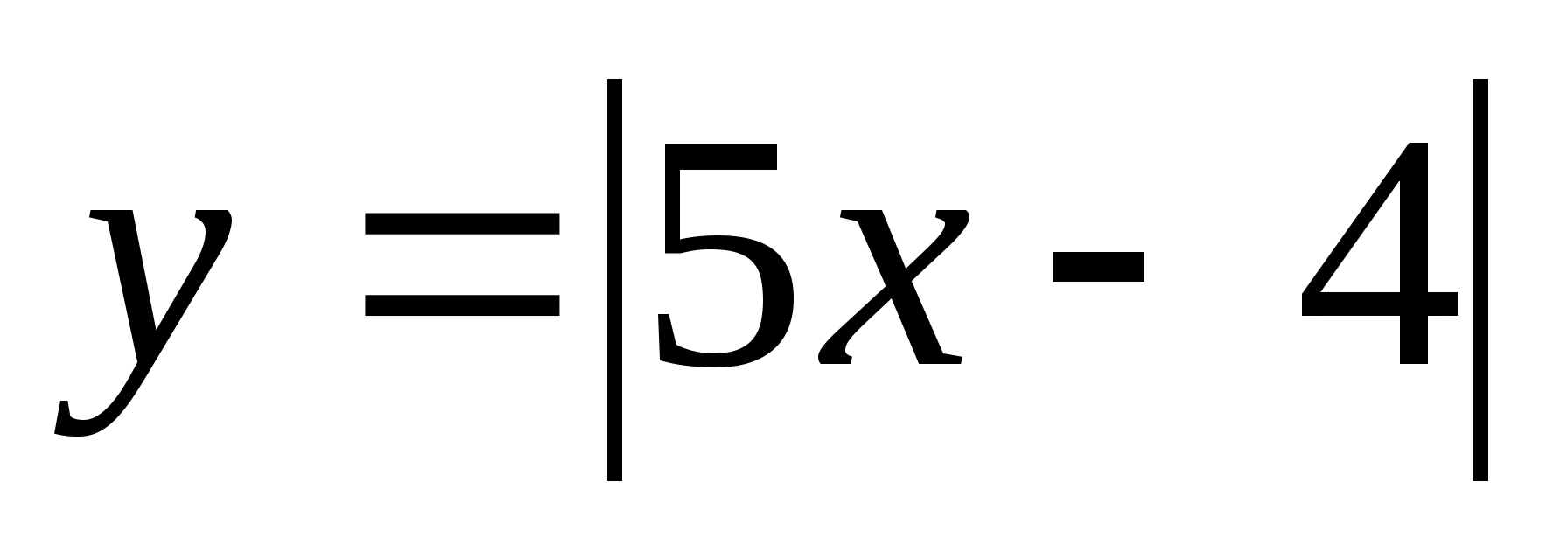
2.

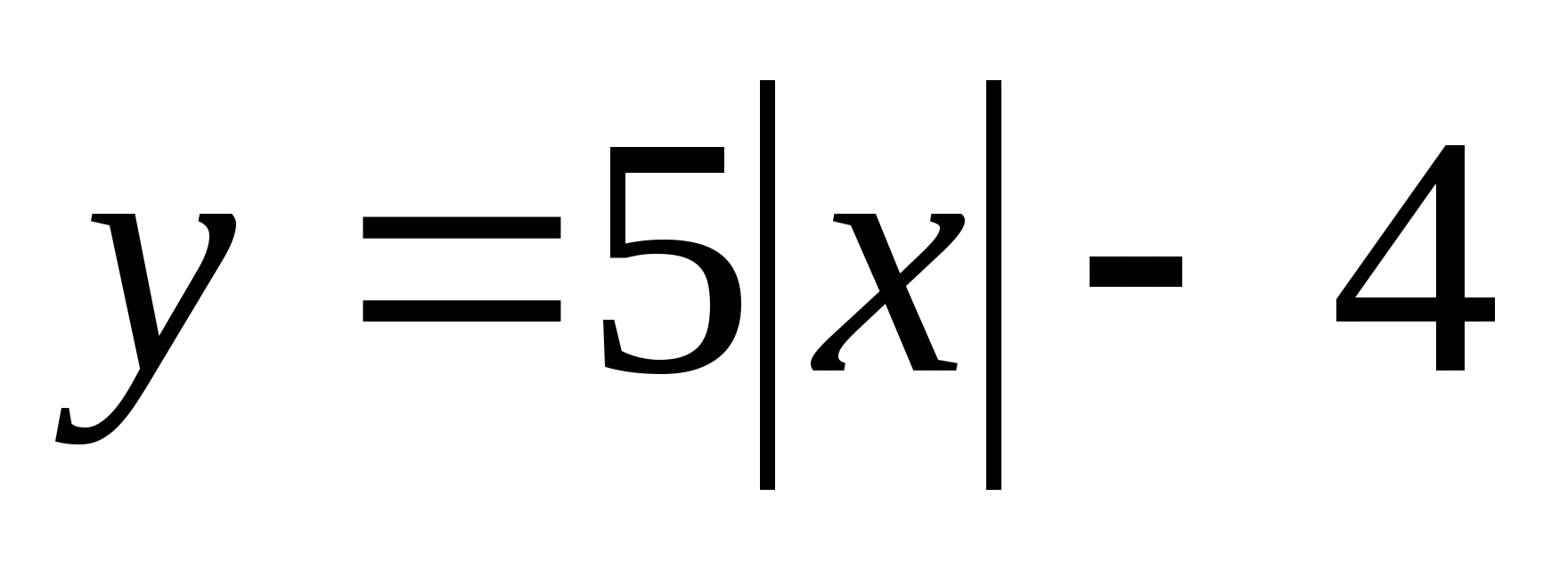
3.

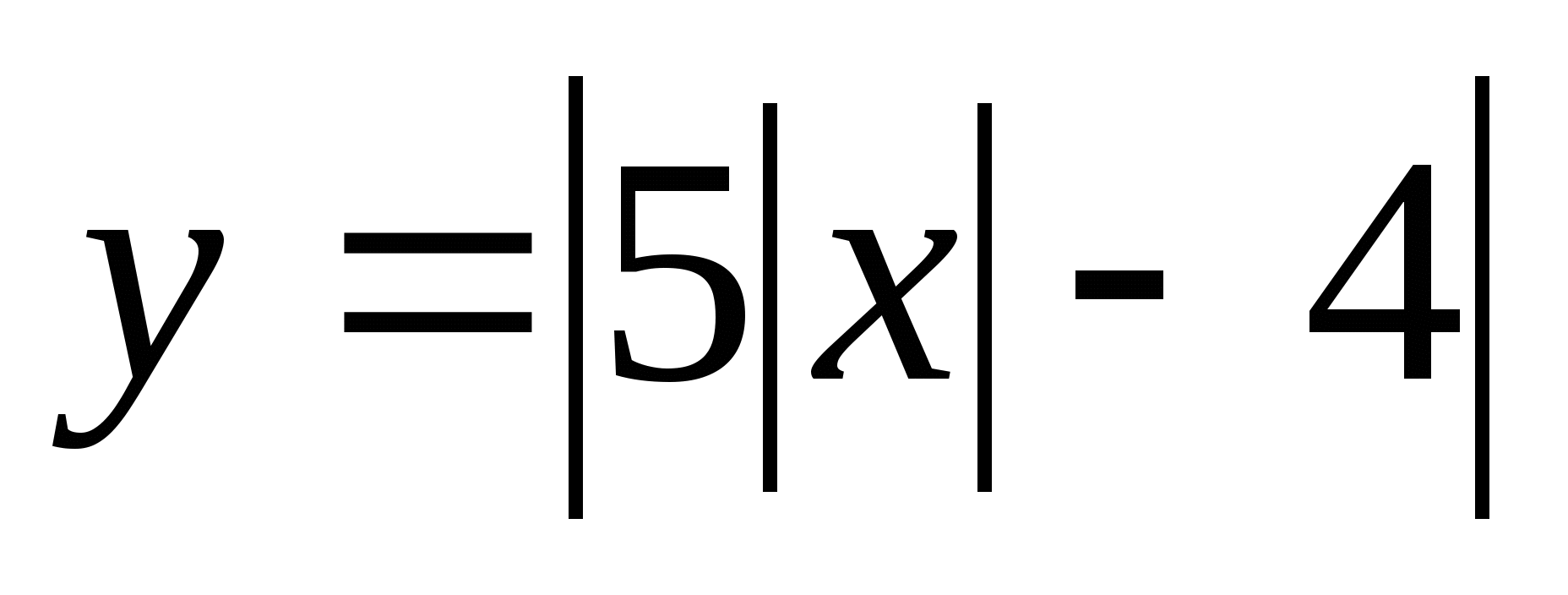
4.

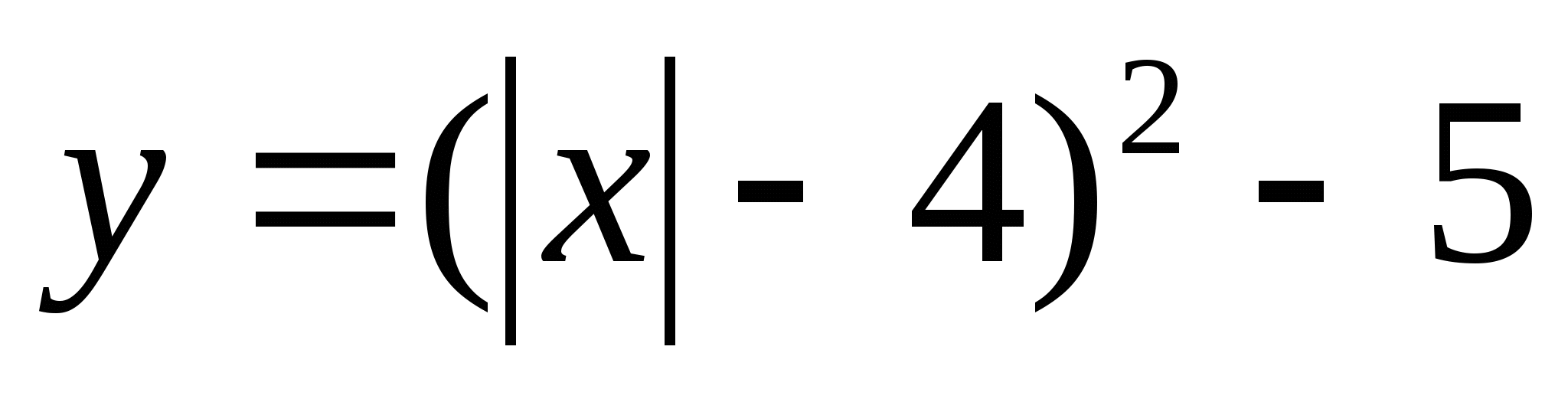
5.

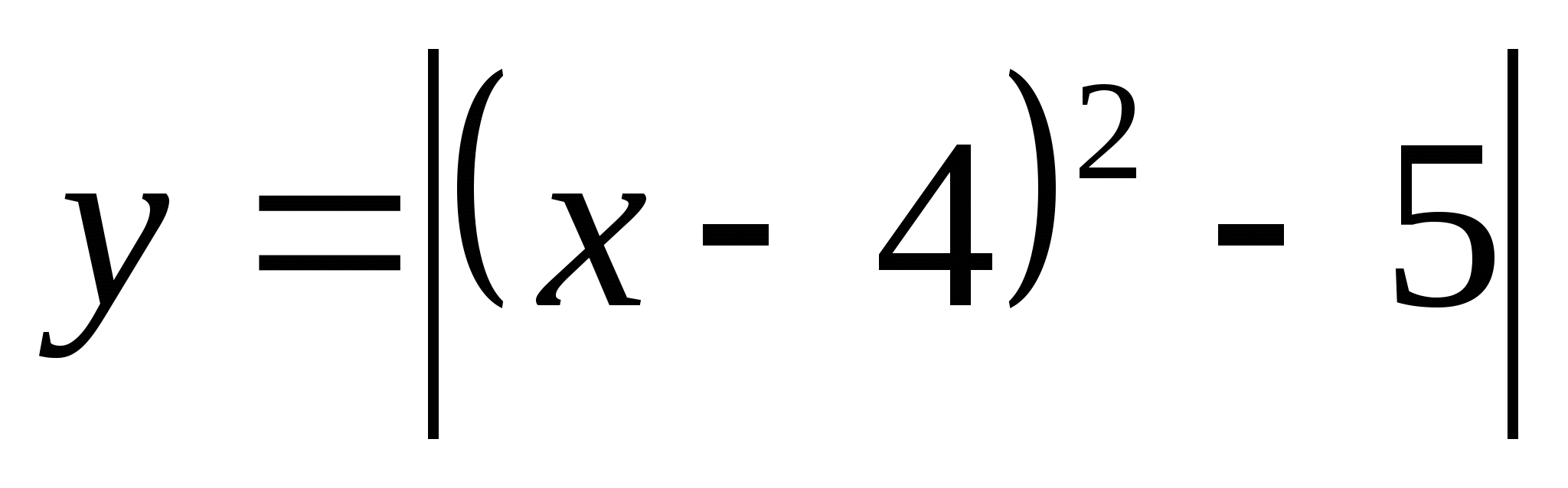
6.