Туынды ұғымының шығу тарихы туралы мәліметтерді оқыту әдістемесі

Туынды ұғымының шығу тарихы туралы мәліметтерді оқыту әдістемесі

Математикада ең маңызды ұғымдардың бірі - функция туындысы ұғымы болып табылады. Туындылар және олардың функциялары математикалық анализ курсының ең негізгі бөлімі болып табылады. Бұл терминмен оқушылар «Алгебра және анализ бастамалары» атты курсында танысады.

Туынды ұғымы бастапқыда шек түрінде анықталады. Бұл жерде оқушыларға «Шек» терминін кезінде Ньютон еңгізгенін, оның lim белгіленуі - латынның limes (меже, шекара) деген сөзінің қысқарған түрі екенін түсіндіріп, айта кету керек. Математикада шексіз аздардың алатын орны ерекше екенін айта кетіп, сондықтан да математикалық анализді кейде шексіз аздар анализі деп атайтынын айтып кеткен жөн. Бірінші сабақта туынды ұғымын еңгізбес бұрын келесі есептерді қарастырған жөн. Олар: химиялық реакцияның жылдамдығы, токтың лездік күші, денелердің лездік жылдамдығын табу, дененің жылуы, қисыққа жанама жүргізу т.с.с. солардың кейбіреулеріне тоқталайық. Функция туындысы түсінігін лездік жылдамдықты анықтау мен жанама жөніндегі есептерді шешуден бастайды.

Қозғалыстың лездік жылдамдығы туралы есеп

Физикадан таныс есепке назар аударайық. Нүктенің түзу бойымен қозғалысын қарастырайық. Айталық нүктенің t уақыт мезетіндегі координатасы болсын. Физика курсынан белгілі болғандай, қозғалыс үздіксіз және біркелкі деп ұйғарайық. Басқаша айтқанда, нақтылы өмірде байқалатын қозғалыстар туралы сөз болып отыр. Өзімізге түсінікті болу үшін тас жолдың түзу сызықты бөлігіндегі материалдық нүктенің қозғалысы туралы есепті қарастырайық.

Мынадай есепті шығарайық: белгілі тәуелділігі бойынша, автомобильдің t уақыт мезетінен басталатын қозғалыстың жылдамдығын анықтау керек (бұл жылдамдық лездік жылдамдық деп аталады). Егер тәуелділігі сызықтық тәуелділік болса, жауабы оңай: кез келген уақыт мезетіндегі жылдамдық дегеніміз жүрілген жолдың уақытқа қатынасы. Егер қозғалыс бірқалыпсыз болса, есепті шығару қиынға соғады.

Материалдық нүкте бірқалыпты қозғалыспен жүретіні айқын. Яғни, ол бірдей уақыт аралықтарында ұзындықтары бірдей жол жүріп өтетін болса, онда бұл қозғалыс жылдамдықты береді. Бұл жылдамдықты табу оңай, ол үшін t уақыт мезетіндегі спидометрдің фотосуретін жасау керек. тәуелділігін біле отырып, жылдамдығын физикалық жолмен табуға болады.

-ден -ға дейінгі ұзақтығы уақыт аралығындағы орташа жылдамдық белгілі

(1.3.1)

Өзіміздің ұйғарғанымыздай дене бірқалыпты қозғалады. Сондықтан былай деп жорамалдау орынды: егер өте аз болса, онда осы уақыт аралығында жылдамдық өзгермейді. ұмтылған жағдайда орташа жылдамдықтың мәні қандай да бір толық анықталған мәнге ұмтылады. Ол нүктені сол нүктенің уақыт мезетіндегі материалдық нүктенің жылдамдығын лездік жылдамдық деп атайды. Сонымен,

Бірақ туындының анықтамасы бойынша:

Сондықтан, лездік жылдамдығы кез келген функциясының дифференциалы болып табылады:

Қысқаша айтқанда, уақыттан координатаға қарағандағы туынды жылдамдықтың өзін береді. Бұл жерде оқушыларға бұған ұқсас есепті кезінде Ньютон шешкенін айта кету керек. Ол туындыны флюксия, ал функцияны флюента деп атағанын түсіндіріп кету керек.

Ток күшіне арналған есеп

Мысалы, тогы бар электрлік тізбекті қарастырайық. уақытта сым арқылы өткен электрдің санын (кулон) арқылы белгілейік. уақытына электрдің саны сәйкес келгендіктен, уақыттың функциясы ретінде электрдің саны алынады. уақыттың бір мезеті, уақыт пен уақыт аралығында сым арқылы өткен электрдің саны. Онда қатынасын токтың орташа күші деп атайды. Егер тізбекте ауыспалы ток болса, онда уақыт мезетіне байланысты - ток та ауыспалы болады. Мұндай ток тізбегі үшін токтың лездік күші деген ұғым еңгізілді.

Токтың лездік жылдамдығын -ның -ға қатынасын шекке апарып қойсақ, онда:

мұндағы ұмтылады.

Химиялық реакцияға арналған есеп

Кейбір заттар химиялық реакцияға түссін. уақытында реакцияға түскен заттардың санын арқылы белгілейік. айнымалының функциясы. Егер уақыттың белгілі бір шамасы болса, мен уақыт аралығындағы реакцияға түскен заттардың саны тең болады. Бұдан қатынасынан реакцияға түскен заттардың орташа жылдамдығы шығады. Бұл қатынасты шекке апарып қойсақ, онда келесі формула шығады: .

«Туынды» ұғымын оқытуда бір-екі физикалық еептерді көрсету жеткілікті. Бұл есептер негізінде «туынды» ұғымы еңгізіледі. Әсіресе қозғалыстың лездік жылдамдығы туралы есептің маңызы зор, өйткені бұл есеп туындының механикалық сипатын ашады, ал функцияның графигіне жүргізілген жанама туындының геометриялық маңызын ашады.

функциясын қарастырайық. интервалында берілген нүкте болсын, және кез келген - нүктелері берілсін. Яғни, . мұндағы - аргумент өсімшесі. Бұл жерде «аргумент өсімшесі» мен «функция өсімшесі» деген ұғымдар пайдаланады. Оқушыларға міндетті түрде бұл ұғымдардың мағынасын түсіндіріп кету керек.

Айталық, - қандай да бір белгіленіп алынған нүктесінің маңайында жатқан еркін алынған нүкте болсын. айырмасын тәуелсіз айнымалының

нүктесіндегі өсімшесі (немесе аргументтің өсімшесі) деп атайды да, деп белгілейді. Сонымен,

бұдан болатыны шығады.

Аргументтің бастапқы мәні өсімшесін алды деп те атайды. Осының салдарынан функциясының өсімшесі деп аталады және символымен белгіленеді, яғни анықтама бойынша

бұдан

белгіленіп көрсетілгенде өсімшесі -тің функциясы болатынына назар аударыңдар.

-тің -ке қатынасын қарастырайық:

Берілген қатынастан -тің барлық мәндері үшін (-ден басқа) интервалында анықталған өсімшесінен өзі шығады. Бұл қатынасты шекке апарып қойсақ, онда келесі теңдік шығады:

Егер қатынасының ұмтылғандағы шегі бар болатын болса, онда бұл шекті функциясының нүктесіндегі туындысы деп аталады.

Бұл анықтаманы келесі түрде жазуға болады:

Осыдан кейін оқушыларға «туынды» терминінің шығу тарихымен таныстыру қажет.

«Туынды» термині derive деген француз сөзінің қазақша сөзбе-сөз аудармасы, оны 1797 ж. Ж. Лагранж (1736-1813) енгізген болатын. Бұл тарихи мағлұматтар оқушылардың математикалық анализ тақырыбына деген қызығушылығын ояту үшін пайдаланылуы тиіс. Мектеп оқулықтарында «дифференциалдау» термині мен туындының функция ретінде қарастырылуы орын алады. Дифференциалдау формуласы енді қандай да бір нүктесі үшін жазылады. Қарап отырсақ кітаптарда нүктесіндегі туынды деп емес ұмтылғандағы туынды деп жазылады. Ең бастысы оқушылар мына екі айырмашылыққа назар аударулары қажет. Мысалы:

1. Нүктедегі туынды;

2. Жанасу нүктесі;

Бірінші сабақта туындыны арқылы емес нүктесі арқылы белгілеп түсіндіру қажет және көрнекі түрде көрсету керек:

Аргументті нүктесі арқылы белгілеген жағдайда туынды функция ретінде қарастырылады. Мысалы, дифференциалдық формуланы қорытып шығаруда келесі шарттарды анықтаған жөн. Егер ұмтылған жағдайда шек болатын болса, онда және -тің мәндері тәуелсіз болады да, тұрақты шама ретінде қарастырылады.

Қолданбалы есептер шығаруда, мысалы, физикалық есептер туынды көмегімен шешіледі. Оған жоғарыда қарастырылған есептер (жылдамдық - жолдың уақыт бойынша алынған туындысы, үдеу - жылдамдықтың уақыт бойынша алынған туындысы т.б) жатады. Бұл есептер туындының қандай айнымалыда орналасқанын көрсетеді.

Сабақтың бірінші кезеңінде бір айнымалы функцияның туындысы қарастырылады. Мектеп оқулығында аралығында анықталған функциясы беріледі. Нүктедегі туындының анықтамасынан кейін функцияны арқылы қарастыруға болады. Бұл жерде оқушылар кейін қиыншылықтарға тап болмас үшін міндетті түрде функцияның оқылуын айта кету керек. функциясының нүктесіндегі туындысы, яғни -тен эф штрих деп оқылады. Тағы бір назар аударарлық жағдай мұндағы белгілеулерін сонау XII ғасырда өмір сүрген Ж. Лагранж еңгізгенін айта кету керек.

Дифференциалдық есептеудің негізгі мақсаты - сызықтық функцияларды қарастыру болып табылады. Бұдан туындыны оқытудың бірінші бағыты анықталады. Ол - сызықтық функцияны тереңдетіп оқыту.

Екінші бағыты - аргумен пен туынды өсімшелерімен жұмыс. Туынды ұғымын еңгізуде оқушылар , (немесе ) қатынастары-тің функциясы екенін түсіну қажет. Әсіресе бұл қатынастардың механикалық және геометриялық мағынасын түсіндіру қажет.

Үшінші бағыты - функцияның графигіне жүргізілген жанама туралы есеп. Бұл есептің математикалық анализ курсында алатын орны ерекше. Өйткені бұл есеп жаратылыстану ғылымының математикалық моделі болып табылады. Сондықтан мектеп курсында бұл есепке ерекше көңіл бөлінеді. Мектеп курсында функцияға жүргізілген жанама есебі туынды ұғымын еңгізуде, оның геометриялық мағынасын анықтауда қолданылады.

Бұл кезеңдердің әрқайсысына тереңірек тоқталайық:

1)Туынды тақырыбын өтпес бұрын оқушылар сызықтық функцияның анықтамасымен, оның графигінің түрлерімен танысады. Мұнда ең маңыздысы оқушылар түзу мен абсцисса осінің арасындағы бұрышты түсіну қажет.

Бұрыш туралы айтқанда 3 жағдайды қарастыру қажет:

1. Егер түзу 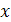осіне параллель болса, онда бұрыш 0-ге тең;

2. Егер түзу 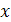осіне перпендикуляр болса, бұрыш 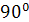-қа тең;

3. Түзу 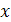осіне параллель де, перпендикуляр да болмаған жағдайда.

Соңғы есепте нүктелер арқылы өтетін қиюшының бұрыштық коэффицеттері қарастырылады. Сөйтіп, бұрыш келесі теңсіздікті қанағаттандырады: . Ескерту: функция графигі төменгі жарты жазықтықта орналасқан жағдайда оқушылар көптеген қателіктер жібереді. Олар жанама бұрышы деп -ті белгілейді (1.3.1 - сурет). Бұл қателіктен оларды сақтау қажет.

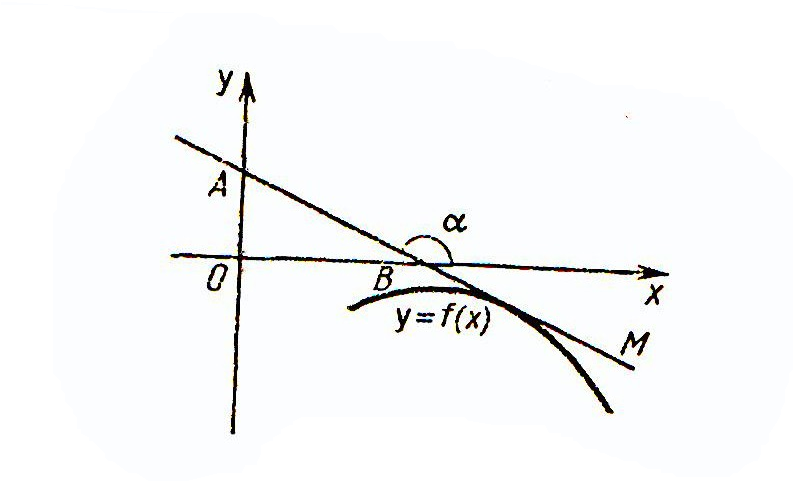
1.3.1 - сурет.

Сызықтық функция мен оның қасиеттерінен келесі заңдылық шығады: егер сызықтық функция формуласы арқылы берілсе, онда осы функция графигінің көлбеу түзуі болатын бұрыштық тангенсі -ға тең болады.

Аргумент өсімшесін еңгізуде функцияны арқылы белгілегені дұрыс. Мұнда оқушыларға айырымды - дельта символымен белгіленетінін айта кету керек және -ті символынан аластатып жазуға болмайтынын түсіндіру керек. Бұл символдың негізгі теңдігін көрнекі түрде жазып кету керек:

, яғни

Геометриялық иллюстрацияның рөліне ерекше назар аударған жөн. Суретте аргумент өсімшесінің оң, теріс, 0-ге тең болатын жағдайлар көрсетілген. (1.3.2 - сурет)

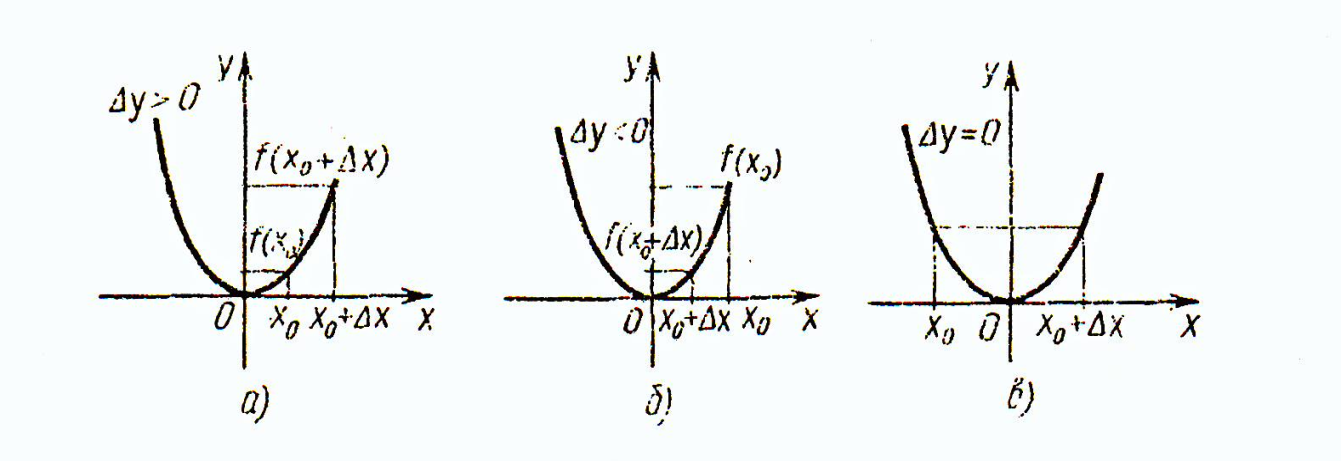
1.3.2 - сурет.

Есептер шығаруда нүктесіндегі функция өсімшесін табу үшін оған сәйкес аргументі мен - ке қатынасын анықтаған жөн. Нақты жағдай үшін оқушыларды - ті дұрыс табуды үйрету керек.

Мысалдар: функция графигінің қатынасын табу керек. Бұл есепте қатынасын -тің функциясы ретінде қарастыруға болады. Бұл функцияның шегі ұмтылады. функциясы нүктесінде дифференциалданатын функциясының графигі - дің маңайында жанаманың кесіндісінен өзгешелігі жоқ, демек, ол және нүктелері арқылы өтетін қиюшының кесіндісіне жақын. нүктесінен өтетін түзуді, оның бұрыштық коэффициенті деп қабылдаймыз.

және нүктелерінен өтетін қиюшының бұрыштық коэффиценті -ке тең, мұнда - аргументтің өсімшесіне сәйкес келетін функциясының нүктесіндегі өсімшесі. функциясы үшін

Енді жанаманың бұрыштық коэффицентін табу үшін, егер нөлге жуықтайтын болса, қандай мәнге жақын болатынын айқындау ғана қалады. мәні -ге жақын екені анық. Олай болса, мәндері өте аз болғанда, қиюшының бұрыштық коэффиценті -ге жақын. болса, шығады. Ізделініп отырған жанама (1; 1) нүктесінен өтетінін ескеріп, жанаманың теңдеуі болады деген қорытындыға келеміз.

Сызықтық функцияның ерекшеліктері: функция үшін қатынасы тұрақты шама және графиктің бұрыш коэффицентіне тең болады. Кері жорамалдауға да болады, егер функцияның қатынасы тұрақты шама болса, онда функция сызықты болады.

Бұл жерде келесіге назар аудару қажет: кейбір аралықта -тің оң мәні үшін -тің оң мәні сәйкес келеді (немесе ), онда функция өспелі болады және кері жорамал да дұрыс. Сәйкес мәндердің шарты бойынша тің ке қатынасы 0-ден үлкен болса, , онда функция өседі және керсінше, егер болса, онда қатынасты өспелі функцияның анықтамасы ретінде анықтауға болса, сол сияқты функцияның кему аралығы да қарастырылады.

Мұнда қатынастың геометриялық мағынасын анықтау қажет. Келесі жағдайларға тоқталайық: осінің кесіндінің ұзындықтары ретінде қарастырамыз. Келесі суретке назар аударайық. (1.3.3 - сурет)

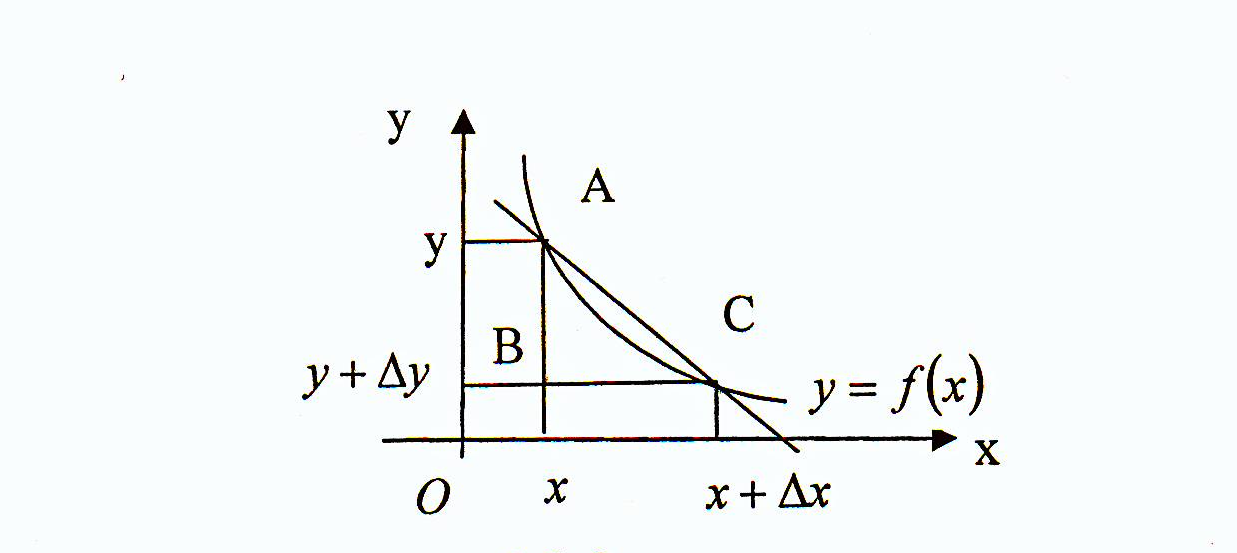
1.3.3 - сурет.

Мұнда ұмтылғандағы жағдай көрсетілген. Үшбұрыш дан келесі теңдік шығады: өйткені Сол сияқты басқа жағдайлар да қарастырылады.

жағдайы жеке қарастырылады. Мұнда қиюшы осіне параллель, көлбеу бұрышы -қа тең. Сондықтан, бұрыштың тангенсі 0-ге тең және қатынасы 0-ге тең.

Осыдан шығады. Мұнда . болғанда функция өседі, мұндағы сүйір бұрыш. Сүйір бұрыштың тангенсі оң мәнді қабылдайды. Сонымен, егер қиюшы функцияның кез келген екі нүктесі арқылы өтетін болса және абсциссалар өсімен сүйір бұрыш жасайтын болса, онда функция өседі.

-тің қатынасының геометриялық мағынасын түсіндіру үшін физикалық есептерді қарастыру қажет. Мысалы, жолдың жүру заңына байланысты есептер қарастыру қажет. - жылдамдық); (- бастапқы жылдамдық, - үдеу); ( g - еркін түсу үдеуі).

Туынды деп - берілген функцияның өзгеру жылдамдығын айтады.

Туындының геометриялық мағынасы: туынды деп - функцияның графигіне жүргізілген осіне жүргізілген жанаманың осіне оң бағытымен жасалған бұрыштың тангенсін атайды.

Туындыны табу амалы дифференциалдау деп атайды. Сөйтіп осы жерде дифференциал ұғымы еңгізіледі. Оның геометриялық мағынасы анықталады. Мектеп оқулығында бұл тақырыптардан кейін келесі тақырыптар қарастырылады: функцияны дифференциалдау ережелері, туындыны табу ережелері, негізгі элементар функциялардың туындыларының кестесі келтіріледі. Бұл материалдардан кейін мектеп оқулығында қосымша ретінде күрделі функциялар мен кері функциялардың туындылары, жоғары ретті туындылар, Ферма мен Ролль теоремасы және Лагранж теоремалары беріледі. Оқушылар үшін бұл күрделі тақырыптардан кейін қарапайым тақырыптар, туындыны функцияны зерттеуде қолдану, функцияның экстремумдарының қажетті және жеткілікті шарттары, функцияның кесіндідегі ең үлкен және ең кіші мәндері, функция графигінің ойыс - дөңестігі және иілу нүктелері, Лопиталь ережесі, туындыны функцияның шегін табу, Тейлор және Моклорен қатары сияқты күрделі тақырыптар беріледі.