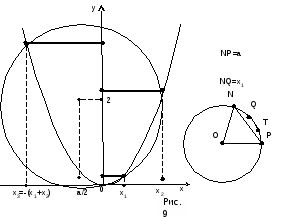- Учителю
- Исследовательская работа Построение трисекции угла.
Исследовательская работа Построение трисекции угла.
Содержание
1. Введение 1
2. Основная часть 2
2.1.Задача: построить трисектрису данного угла 2
2.2. Углы, трисекция которых выполнима с помощью циркуля и линейки 2
2.3. Доказательство неразрешимости трисекции угла с помощью циркуля и линейки в общем виде 3
2.4. Методы решения задачи о трисекции угла 3
2.4.1. Решение способом «вставок» 4
2.4.2. Решение Архимеда 4
2.4.3. Решение Гиппия при помощи открытой им квадратрисы 4
2.4.4. Решение при помощи спирали Архимеда 5
2.4.5. Решение при помощи улитки Паскаля 6
2.4.6. Решение Паппа Александрийского при помощи конхоиды Никомеда 6
2.4.7. Решение Декарта 7
2.4.8. Решение с помощью конических сечений. Метод Шаля 9
2.4.9. Решение с помощью параллельных прямых 9
2.5. Свойство трисектрисы 10
2.6. Инструменты для выполнения трисекции угла 10
3. Заключение 12
4. Список литературы 15
5. Приложения 16
1. Введение
Актуальность исследования. С глубокой древности известны три задачи на построение: задача о трисекции угла, об удвоении куба и квадратуре круга. Они сыграли особую роль в истории математики. В конце концов было доказано, что эти задачи невозможно решить пользуясь только циркулем и линейкой. Но уже сама постановка задачи - «доказать неразрешимость»- была смелым шагом вперед. Вместе с тем предлагалось множество решений при помощи нетрадиционных инструментов. Всё это привело к возникновению и развитию совершенно новых идей в геометрии и алгебре. Немало преуспели в нестандартных и различных приближенных решениях любители математики. Особенно популярны у них были три знаменитые задачи древности. Задачи кажутся доступными любому; вводят в заблуждение лишь их простые формулировки. Проблема решить три «знаменитые задачи» стояла во все времена, она актуальна и сегодня, т.к. задача о делении угла на три равные части возникла из потребностей архитектуры и строительной техники.
Сама жизнь требовала от геометров хорошо разработанной теории и практики построения правильных многоугольников. Строить правильные многоугольники сравнительно просто, когда равные дуги получались делением соответствующих равных центральных углов пополам. И возникали чрезвычайно большие трудности, когда необходимо было получить равные дуги при делении центрального угла на три равные части, тогда перед геометрами возникли чрезвычайно большие трудности, которые привели ученых к специальному рассмотрению задачи о трисекции угла.
В научной литературе наиболее ярко выделятся методы деления угла на три равные части такие, как спираль Архимеда, улитка Паскаля, конхоида Никомеда и другие. Я впервые познакомился с тремя знаменитыми задачами древности в седьмом классе на научно-практической конференции, где ученик 11 класса Салимов Вадим рассматривал задачи на геометрические построения по теме «Решение задач с помощью конических сечений», а прошлом году на городской научно-практической конференции тему геометрических построений продолжил ученик 11 класса Коротков Максим. Меня заинтересовали задачи на построение, поэтому с прошлого года я занимаюсь решением задачи о трисекции угла, которая наиболее интересна для меня. Исходя из выше изложенного, я определил для работы следующие цели и задачи:
Цель исследования - изучение и экспериментальная проверка теоретических основ возможностей построения трисекции угла.
Объект исследования - процесс построения трисекции угла.
Предмет исследования - методы построения трисекции угла.
Проблема исследования заключается в выявлении условий, при которых возможно построение трисекции угла с помощью циркуля и линейки, а при которых невозможно.
Задачи исследования - в соответствии с целью и проблемой исследования я поставил следующие задачи:
-
Изучить развитие идей построения трисекции угла;
-
Определить условия разрешимости задачи о трисекции угла с помощью циркуля и линейки;
-
Изучить теоретические основы неразрешимости задачи о трисекции угла с помощью циркуля и линейки;
-
Изучить геометрические построения трисекции угла с помощью других средств;
-
Найти практическое применение данной задачи;
-
Изготовить прибор для выполнения трисекции угла;
-
Изучить самостоятельно основные формулы тригонометрии.
Методы исследования: сбор, изучение, анализ, обобщение экспериментального и теоретического материала, рефлексивное осмысливание результатов построения выбранными методами.
2. Основная часть
2.1.Задача: построить трисектрису1 данного угла.
Известна следующая легенда. Один пифагореец умирал на чужбине и не мог заплатить человеку, который за ним ухаживал. Перед смертью он велел ему изобразить на своем жилище пятиконечную звезду (она была их опознавательным знаком и символизировала здоровье): если когда-нибудь мимо будет идти пифагореец, он обязательно спросит о ней. И действительно, несколько лет спустя некий пифагореец увидел этот знак и вознаградил хозяина дома.
Но мне кажется, что при составлении рабочих чертежей орнаментов, разного рода украшений, многогранных колоннад и т.д., при строительстве, внутренней и внешней отделке храмов, надгробных памятников и других больших и малых сооружений древние инженеры, художники и архитекторы встретились с необходимостью уметь делить окружность на любое конечное число равных частей, а это довольно часто приводило их к рассмотрению трисекции некоторых углов. Делить угол пополам древние греки умели довольно легко, а вот разделить угол на три равные части оказалось не всегда возможно.
2.2. Углы, трисекция которых выполнима с помощью циркуля и линейки.
Выражение «построения с помощью циркуля и линейки» в геометрии имеет вполне определенный смысл. При этих построениях циркуль используется лишь для проведения окружностей, а линейка - для проведения прямых.
Н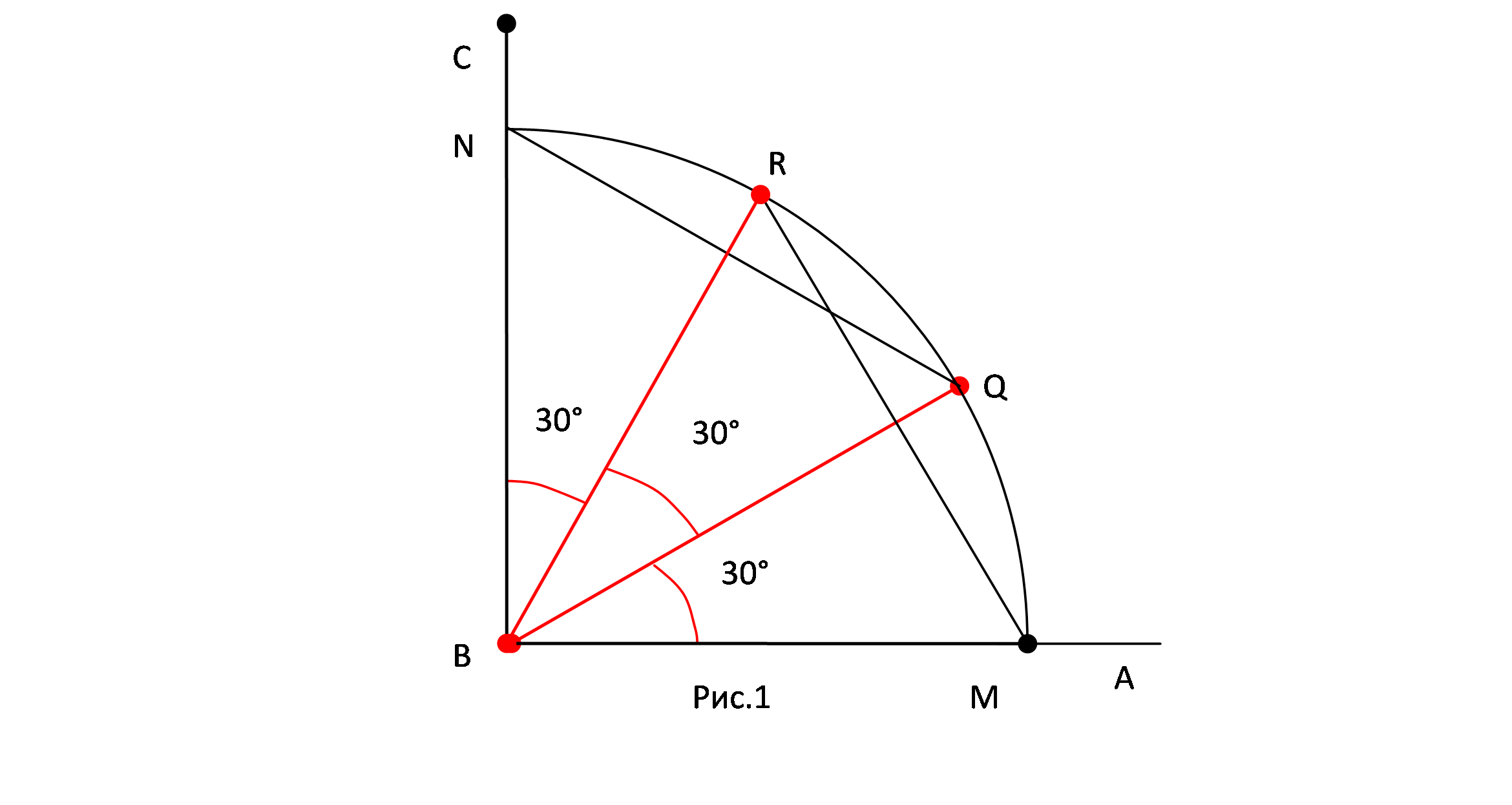 иже я привел
подробное описание построения трисекции угла в 90°. Можно легко
указать бесчисленное множество углов, для которых трисекция
выполнима с помощью циркуля и линейки. Можно, например, с таким же
успехом разделить угол в 45° на три равные части (Приложение №1).
Вообще, трисекция выполнима для углов вида /2n, где n-
целое положительное число.
иже я привел
подробное описание построения трисекции угла в 90°. Можно легко
указать бесчисленное множество углов, для которых трисекция
выполнима с помощью циркуля и линейки. Можно, например, с таким же
успехом разделить угол в 45° на три равные части (Приложение №1).
Вообще, трисекция выполнима для углов вида /2n, где n-
целое положительное число.
Пусть дан прямой угол ABC (рис.1) и требуется разделить его на три равные части, т.е. произвести трисекцию этого угла. Для этого из вершины данного угла B, как из центра, проводим окружность (для нужного построения достаточно четверть окружности). Точки пересечения окружности со сторонами AB и BC соответственно обозначим через M и N. Далее, из точек М и N тем же радиусом делаем засечки R и Q. Теперь соединим хордами М и R, N и Q. Получаем два равносторонних треугольника: ΔВRМ и ΔВQN. Но в равностороннем треугольнике все три угла по 60°. Следовательно, МВR = QВN = 60°. Тогда МВQ = RВN= QВR = 30°. Итак, данный прямой угол удалось разделить на три равные части. Что и нужно было сделать.
2.3. Доказательство неразрешимости трисекции угла
с помощью циркуля и линейки в общем виде
Обозначу данный угол, который нужно разделить на три равные части, через 3. Рассмотрю cos 3.
По известным формулам тригонометрии буду иметь:
cos 3 = cos (+2) = cos cos 2 - sin sin 2 = cos (cos2 - sin2 ) - sin 2sin cos =
=cos3 - cos sin2 - 2sin2 cos = cos3 - 3cos (1 - cos2) = cos3 - 3cos + 3cos3 =
= 4cos3 - 3cos
Итак, cos 3 = 4cos3 - 3cos . Умножая левую и правую части уравнения на 2, получу , 2cos 3 = 8cos3 - 6cos . Пусть теперь 2cos 3=a, а 2cos =x, тогда a = x3 - 3x;
x3 - 3x - a =0.
Когда это уравнение для некоторого а разрешимо в квадратных радикалах, то трисекция соответствующего угла выполнима при помощи циркуля и линейки, и наоборот: если для данного угла выполнима трисекция, то соответствующее уравнение должно быть разрешимо в квадратных радикалах.
Чтобы доказать, что трисекция угла не разрешима в общем виде, достаточно указать хотя бы один угол, который нельзя разделить при помощи линейки и циркуля на три равные части. Предположим, что 3=60°, тогда cos 3=0.5, и уравнение примет вид:
x3 - 3x - 1 = 0.
В алгебре доказывается, что рациональными корнями уравнения могли бы быть +1 и -1, но ни то, ни другое указанному уравнению не удовлетворяет.
Таким образом угол в 60° не может быть разделен на три части с помощью циркуля и линейки; угол в 20° (а следовательно, и угол в 40°) не может быть построен с помощью этих средств решения.
При решении задачи трисекции угла можно ограничиться случаем острого угла, потому что если >90°, то /3 = ( - 90°)/3 + 30°, а угол 30° легко построить циркулем и линейкой.
2.4. Методы решения задачи о трисекции угла
Изучая различную литературу, я старался найти как можно больше решений задачи о трисекции угла. Вот эти решения с их полным описанием.
2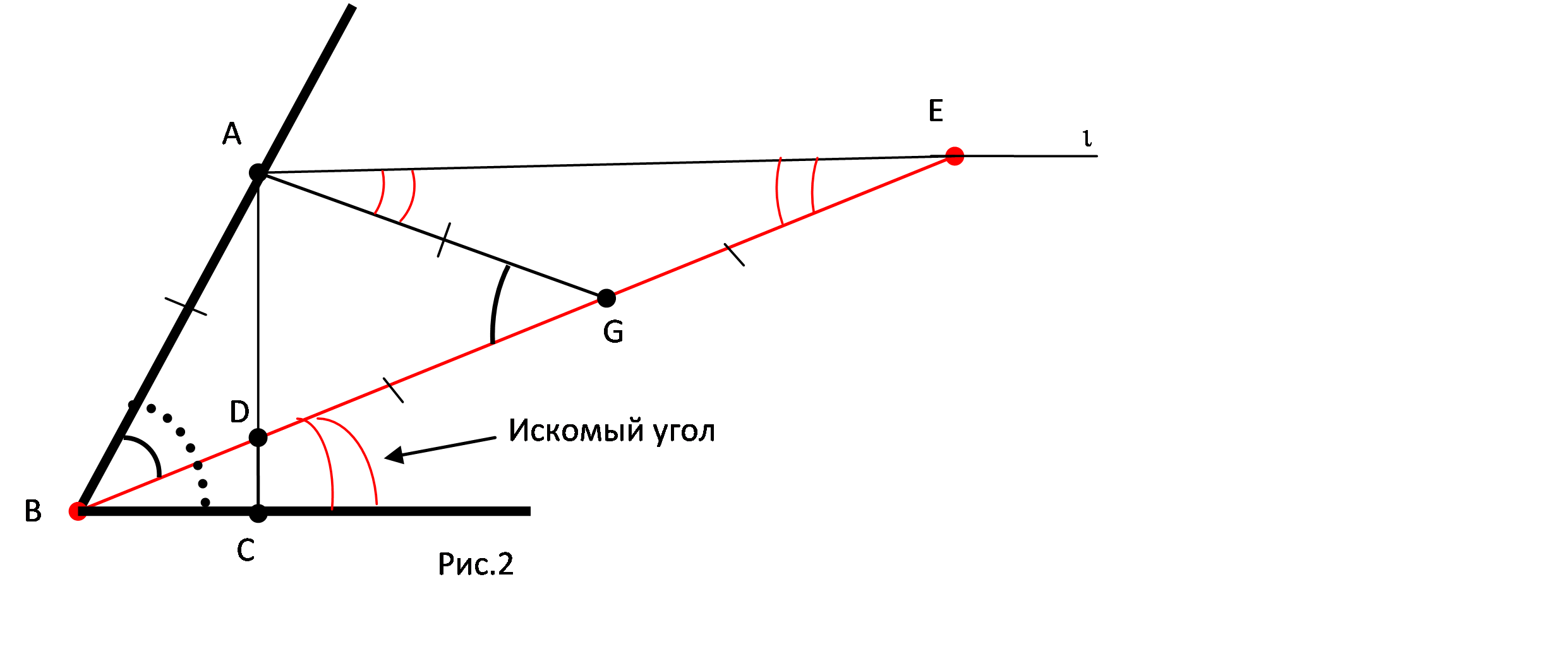 .4.1. Решение
способом «вставок»
.4.1. Решение
способом «вставок»
Возьмем на стороне угла с вершиной В произвольную точку А и опустим из нее перпендикуляр АС на другую сторону (рис. 2). Проведем через точку А луч , сонаправленный с лучом ВС. Вставим теперь между лучами АС и отрезок DE длиной 2АВ так, чтобы его продолжение проходило через точку В. Тогда ЕВС= ABC/3. В самом деле, пусть G- середина отрезка DE. Точка А лежит на окружности с диаметром DE, поэтому AG=GE=AB=DE/2. Треугольники BAG и AGE равнобедренные, поэтому ABG=AGB=2AEG=2EBC, CBE=ABC/3
2.4.2. Решение Архимеда
Д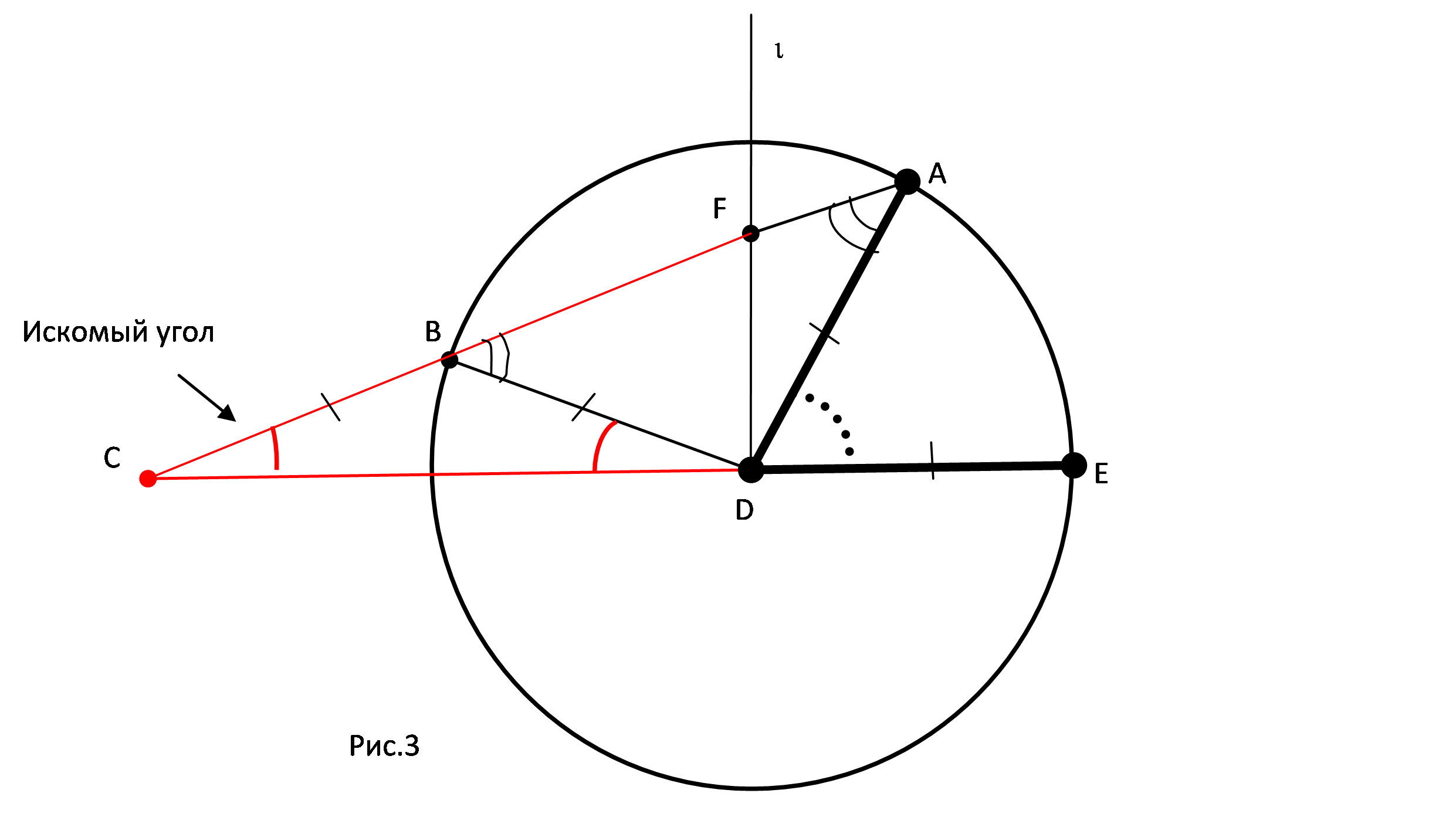 ругое решение
задачи трисекции угла способом «вставок» предложил Архимед. В его
решении нужно вставить отрезок данной длины между прямой и
окружностью, при этом удобно использовать линейку с двумя
делениями, расстояние между которыми равно радиусу окружности.
Рассмотрим угол ADE; можно считать, что D - центр окружности, а
точки А и Е лежат на окружности. Проведем через точку А прямую так,
чтобы окружность и прямая DE высекали на ней отрезок ВС, длина
которого равна радиусу окружности (рис. 3). Тогда BDC=ADE/3. В
самом деле, ADE= ACD+ CAD, а так как треугольники CBD и ADB
равнобедренные, то BCD= BDC и ABD =BAD, поэтому ADE =ACD+
CAD= BDC+2BDC=3BDC.
ругое решение
задачи трисекции угла способом «вставок» предложил Архимед. В его
решении нужно вставить отрезок данной длины между прямой и
окружностью, при этом удобно использовать линейку с двумя
делениями, расстояние между которыми равно радиусу окружности.
Рассмотрим угол ADE; можно считать, что D - центр окружности, а
точки А и Е лежат на окружности. Проведем через точку А прямую так,
чтобы окружность и прямая DE высекали на ней отрезок ВС, длина
которого равна радиусу окружности (рис. 3). Тогда BDC=ADE/3. В
самом деле, ADE= ACD+ CAD, а так как треугольники CBD и ADB
равнобедренные, то BCD= BDC и ABD =BAD, поэтому ADE =ACD+
CAD= BDC+2BDC=3BDC.
2.4.3. Решение Гиппия при помощи открытой им квадратрисы
Квадратриса - плоская трансцендентная прямая, определяемая кинематически.
Трансцендентные прямые - аналитические кривые, не являющиеся алгебраическими, т.е. для которых функция F(x; y) есть многочлен от двух переменных.
К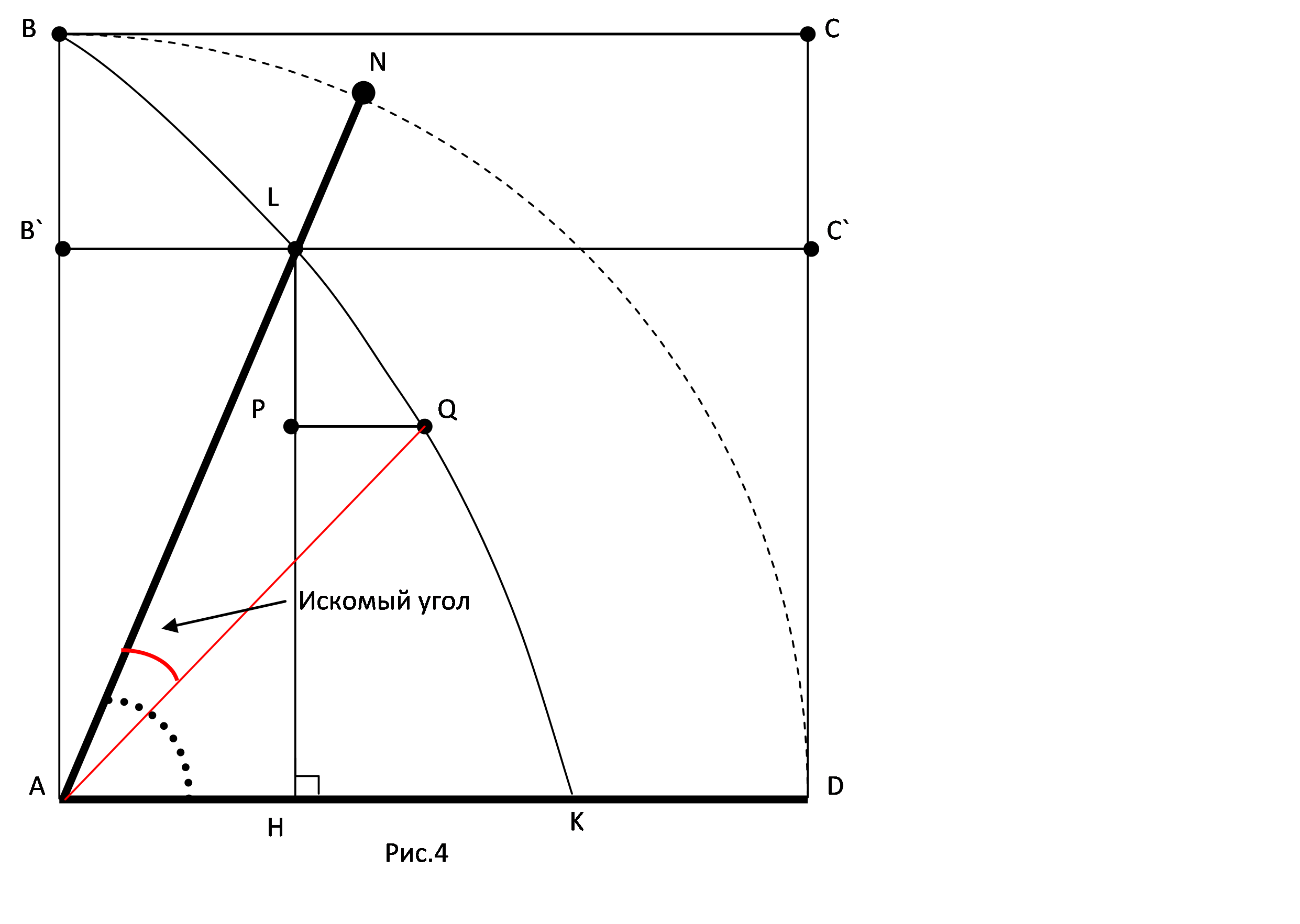 вадратриса
получается следующим образом. Рассмотрим квадрат ABCD. Пусть концы
отрезка ВС равномерно движутся по прямым ВА и CD, а отрезок АВ
равномерно вращается вокруг точки А, причем в положение AD оба
отрезка приходят одновременно (рис. 4). Пусть, далее, в некоторый
момент отрезок ВС переместился в положение В`С`, а отрезок АВ
переместился в положение AN; L - точка пересечения отрезков В`С` и
AN. Гиппий рассмотрел кривую, состоящую из всех точек L. Чтобы
получить треть угла NAD, опустим из точки L перпендикуляр LH на
прямую AD и разделим отрезок LH точкой Р в отношении 1:2. Пусть Q -
такая точка квадратрисы, что PQ BC. Из определения квадратрисы
следует, что LAQ: QAK=LP:PH=1:2 , т. е. AQ - искомый луч и
LAQ=LAK/3.
вадратриса
получается следующим образом. Рассмотрим квадрат ABCD. Пусть концы
отрезка ВС равномерно движутся по прямым ВА и CD, а отрезок АВ
равномерно вращается вокруг точки А, причем в положение AD оба
отрезка приходят одновременно (рис. 4). Пусть, далее, в некоторый
момент отрезок ВС переместился в положение В`С`, а отрезок АВ
переместился в положение AN; L - точка пересечения отрезков В`С` и
AN. Гиппий рассмотрел кривую, состоящую из всех точек L. Чтобы
получить треть угла NAD, опустим из точки L перпендикуляр LH на
прямую AD и разделим отрезок LH точкой Р в отношении 1:2. Пусть Q -
такая точка квадратрисы, что PQ BC. Из определения квадратрисы
следует, что LAQ: QAK=LP:PH=1:2 , т. е. AQ - искомый луч и
LAQ=LAK/3.
2.4.4. Решение при помощи спирали Архимеда
Архимедова спираль - спираль, плоская кривая, траектория точки L(рис. 5), которая равномерно движется вдоль луча OA с началом в O, в то время как сам луч OA равномерно вращается вокруг O.
Э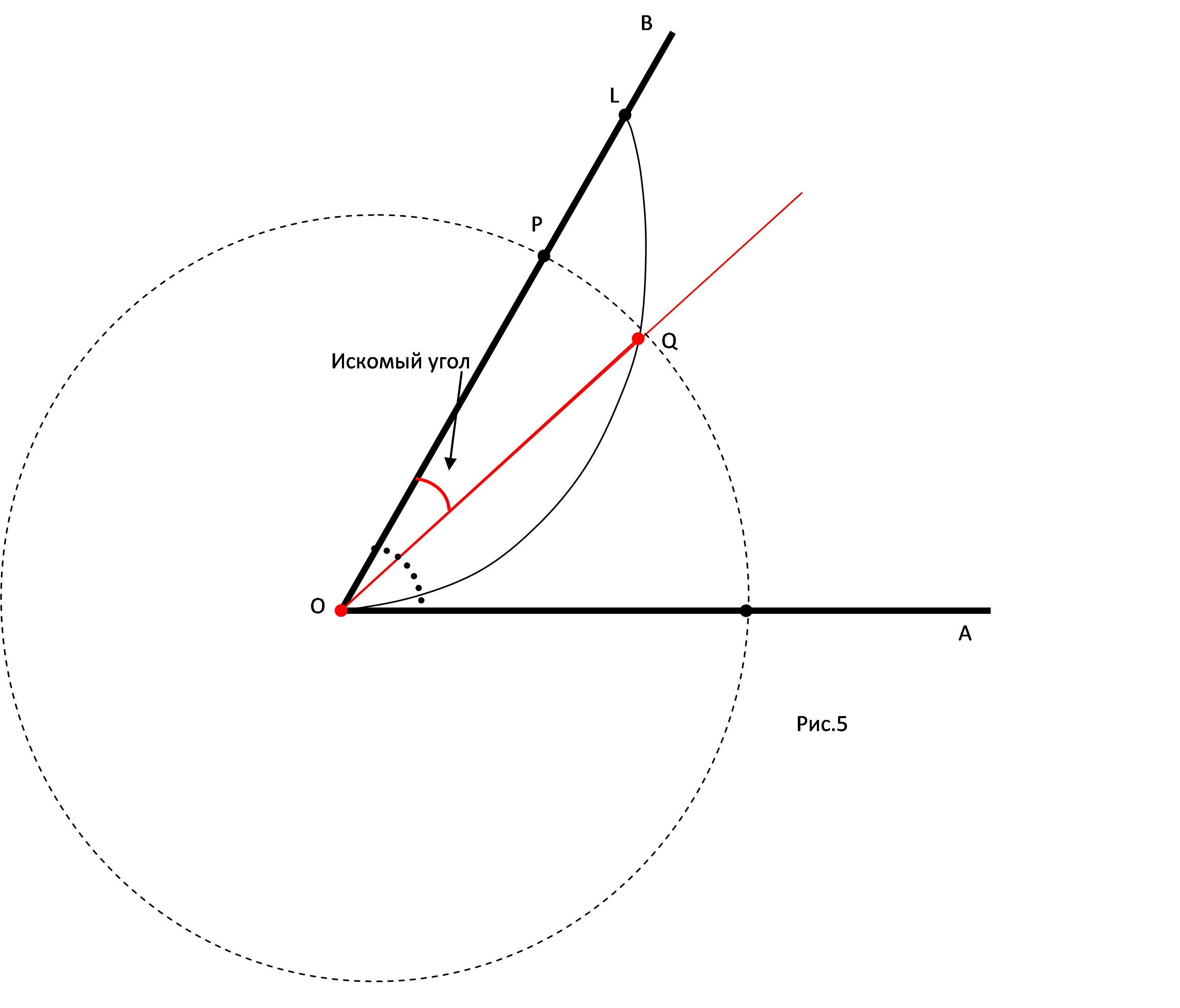 та кривая
получается следующим образом. Пусть луч ОА равномерно вращается
вокруг точки О, а точка L равномерно движется по этому лучу, причем
в начальном положении она находится в точке О (рис. 5). Тогда точка
L движется по спирали Архимеда. Пусть угол АОВ нужно разделить в
заданном отношении. Рассмотрим часть спирали Архимеда, полученную
при вращении луча от начального положения ОА до положения ОВ. Пусть
Р-точка, которая делит OL в отношении 1:2, где L - точка
пересечения луча ОВ и спирали, Q - точка пересечения спирали и
окружности радиуса ОР с центром О. Из определения спирали следует,
что LOQ : QOA = LP:QO = LP : PO= 1:2, т. е. OQ -искомый луч и
LOQ=BOA/3
та кривая
получается следующим образом. Пусть луч ОА равномерно вращается
вокруг точки О, а точка L равномерно движется по этому лучу, причем
в начальном положении она находится в точке О (рис. 5). Тогда точка
L движется по спирали Архимеда. Пусть угол АОВ нужно разделить в
заданном отношении. Рассмотрим часть спирали Архимеда, полученную
при вращении луча от начального положения ОА до положения ОВ. Пусть
Р-точка, которая делит OL в отношении 1:2, где L - точка
пересечения луча ОВ и спирали, Q - точка пересечения спирали и
окружности радиуса ОР с центром О. Из определения спирали следует,
что LOQ : QOA = LP:QO = LP : PO= 1:2, т. е. OQ -искомый луч и
LOQ=BOA/3
2.4.5. Решение при помощи улитки Паскаля
В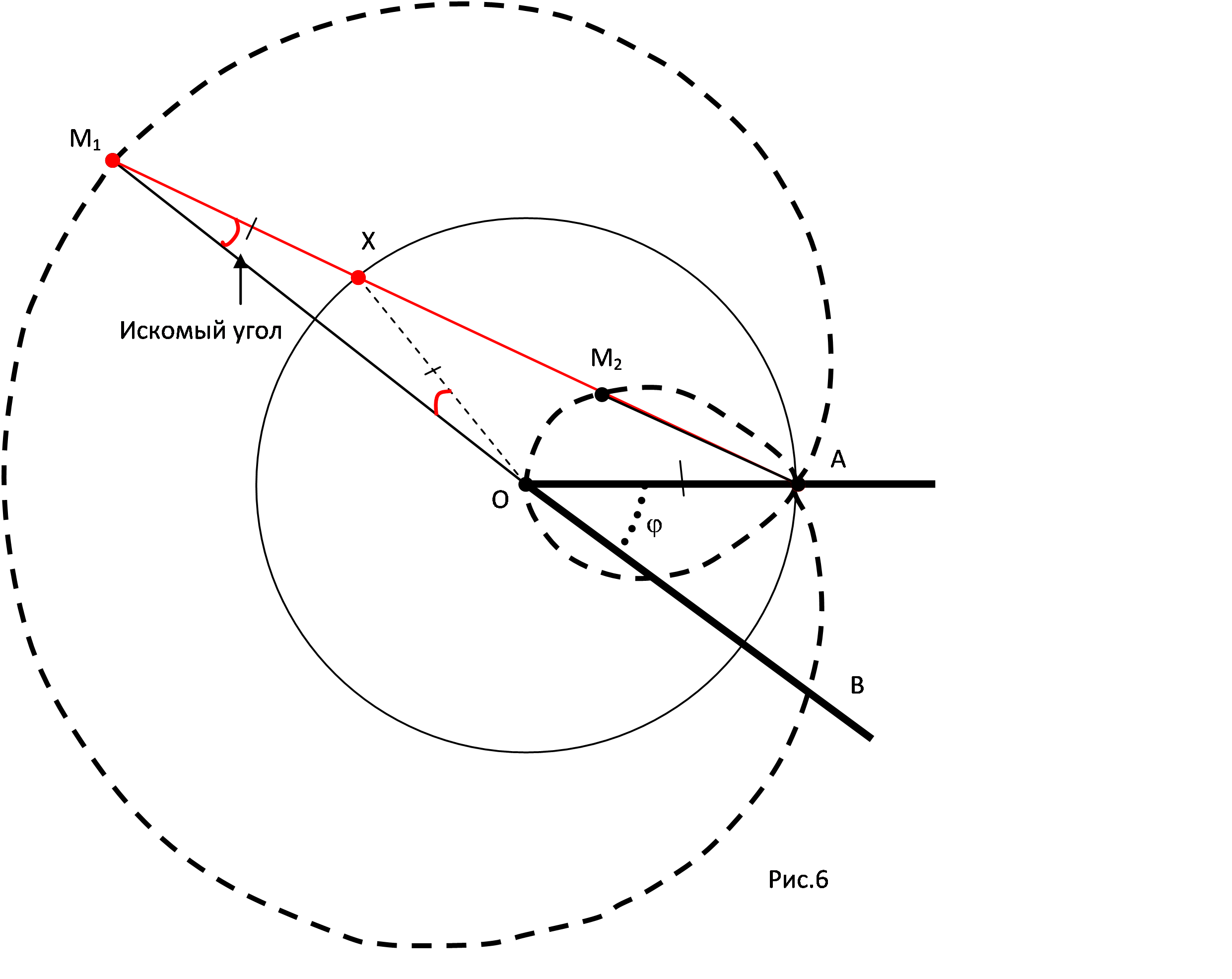
озьмем на окружности радиуса R точку А и проведем через нее прямую . Прямая пересекает окружность в точках X и А (если -касательная, то Х=А). Пусть М1 и М2 - такие точки прямой , что ХМ1 = ХМ2 = а, где а - фиксированное число. Множество всех точек М1 и М2 (для всех прямых ) называют улиткой Паскаля.
Нас будет интересовать случай, когда a = R (рис. 6). Пусть векторы XM1 и АХ сонаправлены, В-точка на продолжении отрезка М1О за точку О. Так как треугольники M1XO и ХОА равнобедренные, то OAX=2OM1A и AOB= OM1A+ OAX= = 3OM1A. Поэтому для трисекции угла , где 0<</2, можно поступить следующим образом. Возьмем точку В так, что АОВ = . Пусть прямая ОВ пересекает сплошную часть улитки Паскаля в точке М1 (пунктирная часть улитки Паскаля соответствует таким точкам М2, что векторы ХМ1 и АХ противоположно направлены). Тогда OM1A=/3
2.4.6. Решение Паппа Александрийского при помощи конхоиды Никомеда
Конхоида Никомеда ― конхоида прямой, плоская алгебраическая кривая 4-го порядка (т.е. задаётся уравнением четвертой степени). Конхоида имеет две ветви, сама прямая конхоиды является асимптотой обеих ветвей.
Пусть острый угол АОВ требуется разделить на три равные части, причем эту трисекцию надо произвести при помощи конхоиды Никомеда. Зная принцип построения конхоиды Никомеда (Приложение №2), поступим так, как указывал Папп Александрийский. На одной из сторон данного угла, например на стороне ОB, возьмем произвольную точку С и из нее на прямую ОА опустим перпендикуляр СD (рис.7). Теперь построим одну ветвь (правую) конхоиды Никомеда, приняв точку О за полюс, прямую СD за базис, а отрезок, равный 2OС, за параметр. Эта конхоида пересечет стороны данного угла в точках Е и F. Через точку С проведем прямую, параллельную DЕ, которая пересечет конхоиду в некоторой точке K. Соединим точку K с точкой О. Полученный угол АОК и будет составлять одну треть данного. Докажем это. Прежде всего обозначим точку пересечения прямых OK и СD через L. Середину отрезка LК обозначим через М и соединим ее прямой с точкой С. Нужные нам углы, как показано на чертеже, обозначим цифрами 1, 2, 3, 4, 5.Остается доказать, что угол 2 в два раза больше угла 1. Действительно, принимая во внимание свойство конхоиды, будем иметь:
LК = DЕ = 2OС.
Далее,
LК = 2LM и СМ = МK.
Следовательно,
4 = 5 (свойство равнобедренного треугольника),
5 = 1 (свойство параллельных прямых),
2 = 3 (свойство равнобедренного треугольника).
Далее, 3 = 4 +5=25 (свойство внешнего угла треугольника), или 2 = 21,
т . е. угол АОК
составляет одну треть угла АОВ, что и требовалось доказать.
. е. угол АОК
составляет одну треть угла АОВ, что и требовалось доказать.
B
F
Рис.7

K








C
4
5
M
3
L
2



Искомый угол
1
Р

O
A
D
Eис.7
2.4.7. Решение Декарта
В связи с постепенным формированием алгебры математики проявляли все больший интерес к уравнениям, особенно к кубическим. В XI в. ими было получено уравнение трисекции угла (т. е. соотношение между sin 3а и sin а) и тем самым было показано, что задача трисекции угла сводится к решению кубического уравнения.
Пусть точки Q и Т делят дугу NР окружности с центром О на три равные части, радиусы ОQ и ОТ пересекают хорду NР в точках R и U, а прямая, проходящая через точку Q параллельно прямой ТО, пересекает эту хорду в точке S (рис.8).
Так как QNR = ( ![]() QТ+
QТ+![]() ТР)/2
=
ТР)/2
=![]() NQ = NOQ, то
треугольники NOQ, QNR. и RQS являются подобными равнобедренными
треугольниками. Поэтому NO : NQ = NQ : QR = QR : RS. Если NO=1 и NQ
= z, то QR=z2 и RS=z3. Ясно также, что NP +
SR= NR +(SR + RU) + UP= NQ + QT +TP= 3NQ, т.е. NP= 3z -
z3.
NQ = NOQ, то
треугольники NOQ, QNR. и RQS являются подобными равнобедренными
треугольниками. Поэтому NO : NQ = NQ : QR = QR : RS. Если NO=1 и NQ
= z, то QR=z2 и RS=z3. Ясно также, что NP +
SR= NR +(SR + RU) + UP= NQ + QT +TP= 3NQ, т.е. NP= 3z -
z3.
Д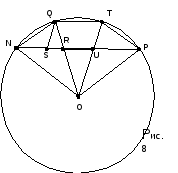 ля построения
корней уравнения x3=рx+q Декарт рассматривал точки
пересечения параболы у = х2 и окружности с центром в
точке (q/2, (p+1)/2), проходящей через начало координат; корни
уравнения являются отличными от нуля проекциями на ось Ох этих
точек пересечения. Кроме того, если точки Q и Т делят на три равные
части дугу NР окружности радиуса 1 и NР = а, NQ= x, то
х3 = 3х - а. Поэтому для трисекции угла Декарт предложил
следующее построение. Пусть нужно разделить дугу NР единичной
окружности на три равные части. Рассмотрим точки пересечения
параболы у = х2 и окружности с центром ( - а/2, 2),
проходящей через начало координат (рис. 9). Если а = NР = 2sin 3.
и 0 3 /2, то корнями уравнения х3=3х- а являются
числа x1 = 2 sin, х2 = 2 sin( + 2/3)= -sin
+ 3 cos и x3 = sin( + 4/3) =- sin - 3 cos = -
(х1 + х2). Положительные корни х1
и х2 Декарт называет «истинными» (число х2 =
2 sin( + 2/3) положительно, так как + 2/3/6 + 2/3< ), а
корень x3= - (x1+х2) он называет
«ложным». В качестве искомого отрезка NQ нужно взять меньший из
положительных корней (второй положительный корень позволяет
разделить на три равные части дугу, дополняющую исходную дугу до
полной окружности).
ля построения
корней уравнения x3=рx+q Декарт рассматривал точки
пересечения параболы у = х2 и окружности с центром в
точке (q/2, (p+1)/2), проходящей через начало координат; корни
уравнения являются отличными от нуля проекциями на ось Ох этих
точек пересечения. Кроме того, если точки Q и Т делят на три равные
части дугу NР окружности радиуса 1 и NР = а, NQ= x, то
х3 = 3х - а. Поэтому для трисекции угла Декарт предложил
следующее построение. Пусть нужно разделить дугу NР единичной
окружности на три равные части. Рассмотрим точки пересечения
параболы у = х2 и окружности с центром ( - а/2, 2),
проходящей через начало координат (рис. 9). Если а = NР = 2sin 3.
и 0 3 /2, то корнями уравнения х3=3х- а являются
числа x1 = 2 sin, х2 = 2 sin( + 2/3)= -sin
+ 3 cos и x3 = sin( + 4/3) =- sin - 3 cos = -
(х1 + х2). Положительные корни х1
и х2 Декарт называет «истинными» (число х2 =
2 sin( + 2/3) положительно, так как + 2/3/6 + 2/3< ), а
корень x3= - (x1+х2) он называет
«ложным». В качестве искомого отрезка NQ нужно взять меньший из
положительных корней (второй положительный корень позволяет
разделить на три равные части дугу, дополняющую исходную дугу до
полной окружности).
2.4.8. Решение с помощью конических сечений. Метод Шаля
Пусть требуется разделить угол AOB на три равные части.
О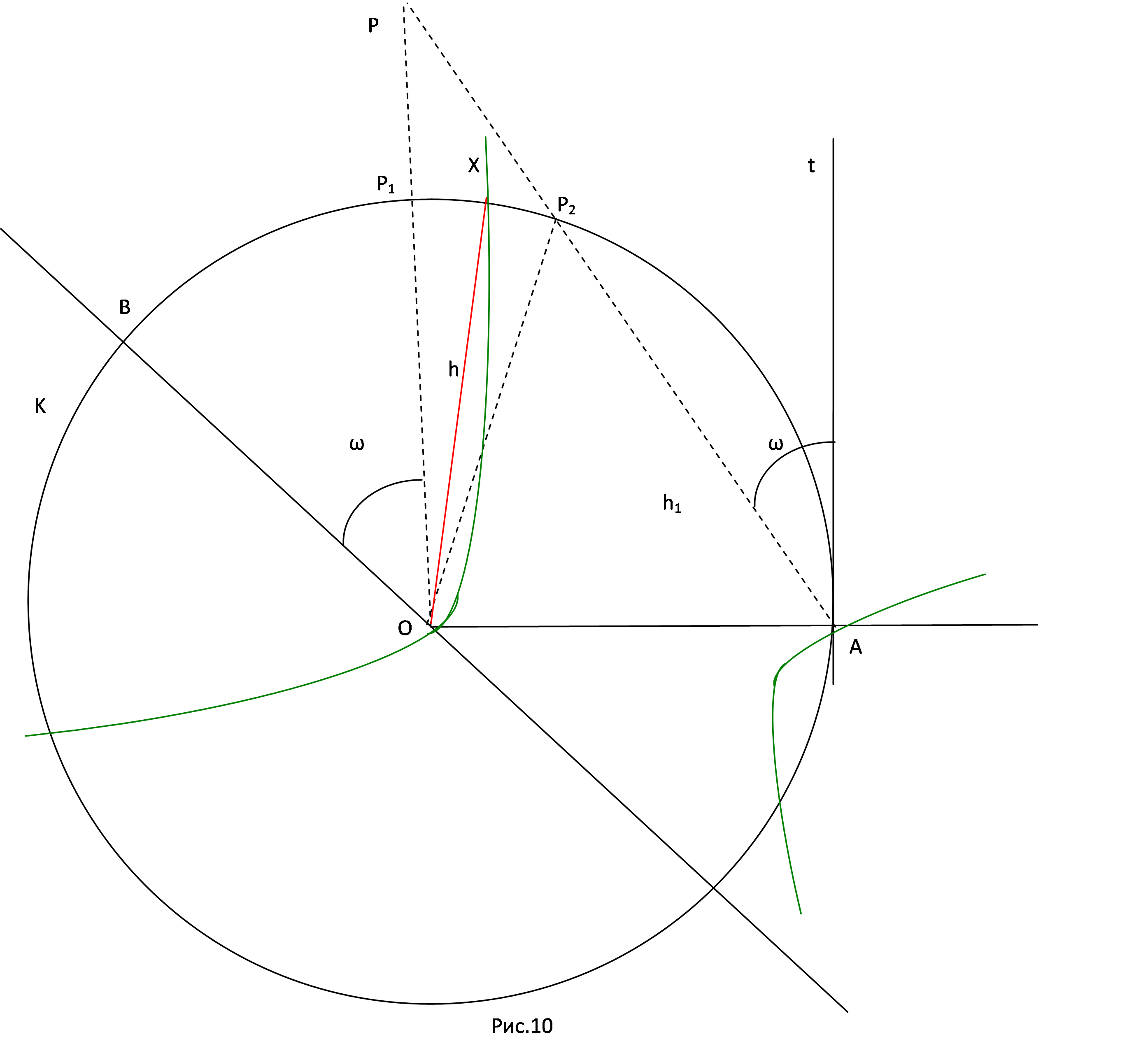 писываем
вокруг О (Рис.10) произвольным радиусом окружность К и в А проводим
к ней касательную t.Затем при О строим на ОВ произвольный угол ω и
при А на t- тот же угол ω, но в
писываем
вокруг О (Рис.10) произвольным радиусом окружность К и в А проводим
к ней касательную t.Затем при О строим на ОВ произвольный угол ω и
при А на t- тот же угол ω, но в
противоположном направлении.
Получаемая таким путем точка пересечения Р при изменении ω описывает некоторую кривую h- гиперболу Шаля. Если X есть одна из точек пересечения гиперболы h с окружностью K, то
BOX=BOA/3.
Именно, если Р1 и Р2 суть точки окружности К, отвечающие точке Р, то всегда
АОР2=2ВОР1. Если теперь точки Р1 и Р2 совпадают в одной точке X, то AOX= 2BOX.
2.4.9. Решение с помощью параллельных прямых
К убические
уравнения и сложные прямые, типа спиралей и конхоид, - это хорошо,
но вот еще один метод трисекции угла, которым может овладеть любой
ученик. Жаль, но этот метод подходит только для острых углов.
убические
уравнения и сложные прямые, типа спиралей и конхоид, - это хорошо,
но вот еще один метод трисекции угла, которым может овладеть любой
ученик. Жаль, но этот метод подходит только для острых углов.
Для такого решения задачи необходимо по линейке с параллельными рёбрами внутри угла провести ряд линий, параллельных его обеим сторонам. Точки взаимного пересечения таких линий сразу разделят угол на любое искомое число равных частей.
Также можно провести трисекцию угла с помощью номографии (Приложение №3).
2.5. Свойство трисектрисы
Т еорема
Морлея: точки пересечения смежных трисектрис углов произвольного
треугольника являются вершинами равностороннего треугольника.
еорема
Морлея: точки пересечения смежных трисектрис углов произвольного
треугольника являются вершинами равностороннего треугольника.
Доказательство: для доказательства используется кардиоиды. Морлей установил, что множество центров кардиоид, касающихся всех трёх сторон треугольника ABC, представляет собой совокупность девяти прямых, разбивающуюся на три тройки параллельных прямых, причем прямые из разных троек пересекаются под углом 60°. Ясно, что при пересечении этих прямых образуется 27 равносторонних треугольников. Один из них и есть «треугольник Морлея».
Кардиоиды - это плоская линия, которая описывается фиксированной точкой окружности, катящейся по неподвижной окружности такого же радиуса.
Но это не всё. Трисектрисы обладают еще некоторыми интересными свойствами, доказательство которых не сложно. Я приведу их в качестве задач ( Приложение №4).
2.6. Инструменты для выполнения трисекции угла
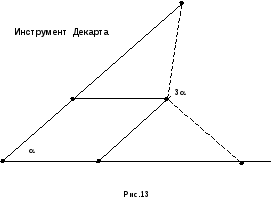
И



 нструмент
Джованни Чева.
нструмент
Джованни Чева.

Рис.14
Инструмент изготовленный мною
для выполнения трисекции угла.

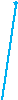

3
Голубые рейки образуют данный угол (который нужно разделить) и могут двигаться по красным рейкам.
Красные образуют искомый угол (треть данного угла) и за счёт шарниров могут поворачиваться.
Точки - это шарниры.
3. Заключение
Практическая значимость работы, на мой взгляд, состоит в следующем:
1. Показаны частные случаи решения задачи о трисекции угла с помощью циркуля и линейки.
2. Доказана неразрешимость данной задачи для произвольного угла при помощи циркуля и линейки.
3. Предложены различные методы решения задачи.
4. Найдено практическое применение данной задачи.
5. Найдены и обобщены теоретические обоснования разрешимости задачи о трисекции угла.
6. Проведен социологический опрос среди учащихся 9 М и их родителей, а также учителей математики школы №8 об актуальности изучения данной задачи. Результаты приведены ниже в таблицах.
Опрос учащихся 9 М класса МОУ «СОШ №8» (23 человека).1. С помощью параллельных прямых - 9.
2. Спираль Архимеда - 4.
3. Метод «вставок» - 4.
4. Улитка Паскаля - 3.
5. Конхоида Никомеда - 3.
7. Хотели бы вы дальше продолжать знакомство с задачами на построение и почему?
Положительно ответили 19 человек, самыми популярными ответами оказались:
1. Развивает понимание теории.
2. Развивает логическое мышление.
3. Умение пользоваться вспомогательными средствами.
4. Для дальнейшей учёбы в будущем.
Опрос родителей 9 М класса МОУ «СОШ №8» (23 человека).Наиболее частые ответы:
1.Это первый шаг использования в геометрии и инновационно-компьютерных технологиях.
2.Возможность заниматься творческой деятельностью.
3.Учиться проводить исследования.
Опрос учителей математики МОУ «СОШ №8» (10 человек).3 метода- 4 человека,
более 3 методов- 6 человек.
3.Нужно ли знакомить учащихся с данной задачей?
Все ответили положительно. Решение данных задач можно рассматривать на элективных курсах и на внеклассной работе по математике, в исследовательской деятельности учащихся.
4.Что дает учащимся умение решать задачи на построение?
1.Развивает логическое мышление, пространственное воображение.
2.Расширяет кругозор.
3.Расширяет базовый курс знаний геометрии, способствует подготовке учащихся к дальнейшему обучению в математических классах, а в дальнейшем и в вузах.
4.Открывает простор для конструктивной, экспериментальной, творческой деятельности.
5.Позволяет ввести в процесс новые формы работы.
6.Учащиеся получают инструмент для геометрических открытий, а учитель - замечательное средство обучения.
7.Учащиеся могут находить закономерности в наблюдаемых геометрических явлениях, самостоятельно формулировать утверждения для последующего доказательства.
8.Учащиеся могут подтверждать уже известные факты науки, но неизвестные им, и применять их на практике.
7. Сравнил точность построения трисекции угла различными способами. Результаты приведены ниже в таблице.
Результаты точности построения трисекции угла (трети выбранного угла).Достоверность работы обеспечивается:
1. Моим личным участием, начиная с изучения научной литературы и проведения необходимых доказательств, до построения трисектрисы угла всеми рассмотренными методами;
2. Рефлексивные анализы изученной научной литературы, что позволило мне сделать необходимые теоретические обобщения;
3. Опорой на ведущие положения и достижения известных математиков в области решения данной задачи;
Анализ развития идей построения трисектрисы угла показал, что имеются все необходимые условия для возможности изучения данной темы во внеурочное время. Более точным решением данной задачи, на мой взгляд, является решение с помощью квадратрисы; это подтверждается приведёнными в таблице результатами погрешности, но на практике более удобен способ параллельных прямых, а также способ построения с помощью инструмента, например такого как, инструмент Декарта.
4. Список литературы
1. А. Адлер. Теория геометрических построений. Санкт-Петербург. Учебно-педагогическое издательство НАРКОМПРОСА РСФСР, 1940.
2. А.Александров, А. Вернар, В.Рыжик. Геометрия. Москва «Просвещение», 1991.
3. В. Прасолов. Три классические задачи на построение. Москва «Наука», 1992.
4. П. Савин. Математика. Энциклопедия для детей. Москва «Аванта +», 1998.
5. П. Савин. Энциклопедический словарь юного математика. Москва. Педагогика-Пресс, 1999.
6. В. Чистяков. Три знаменитые задачи древности. Москва «Просвещение», 1963.
5. Приложения
1</<span> Трисектриса - луч, проходящий внутри угла и делящий его на два угла в отношении 1:2, т.е. делящий угол на три равные части.