Технологическая карта работы над задачей на тему Операции над множествами (8 класс)

Модуль 10.

Изучение вероятностно-стохастической линии в школьном курсе математики

Выполнил работу: Холодов Сергей Алексеевич, МОУ Дровянинская СОШ Забайкальского края

Контрольная работа

Задание. Разработайте систему целесообразно подобранных задач по «Вероятностно-стохастической линии» по одному из разделов для определенной возрастной группы. Смоделируйте учебную ситуацию (в рамках урока или внеучебного занятия) по работе над задачей, направленную на формирование универсальных учебных действий. Модель ситуации представьте в виде технологической карты работы над задачей.Учитель

Холодов Сергей Алексеевич

Класс

7

Раздел

Множества

Результаты обучения по разделу

Личностные

Метапредметные

Предметные

-умеют грамотно излагать свои мысли в письменной и устной речи речи;

-понимают смысл поставленной задачи;

-проявляют креативность мышления, находчивость;

- осознают важность и необходимость знаний для человека;

-умеют контролировать процесс и результат своей деятельности.

-умеют видеть математическую задачу в окружающем мире;

-находят различные стратегии решения задач;

-создают алгоритмы для решения математических задач;

- умеют планировать свою деятельность и осуществлять ее.

- умеют выделять множества, подмножества;

- умеют правильно записывать операции над множествами;

- умеют правильно строить круги Эйлера для заданных множеств;

- умеют находить объединение множеств, пересечение множеств, разность множеств аналитическим и графическим способами;

-умеют выполнять устные и письменные вычисления;

- умеют преобразовывать рациональные выражения;

- умеют решать линейные уравнения;

Система задач

Знакомая задача

Малознакомая задача

Незнакомая задача

Заданы два множества: А {2, 3, 4, 5, 6} и В {2, 4, 6, 7, 8}. Определить множество А∩В, АВ, А\В, В\А.

Ответ:

А∩В={2,4,6}

АВ={2,3,4,5,6,7}

А\В={5}

В\А={7}

По данным промежуткам А [4;+∞) и В (2;7] на числовой прямой определить множество А∩В, АВ, А\В, В\А

Ответ:

А∩В=[4, 7]

АВ=(2, ₊∞ ]

А\В=(7;+ ∞]

В\А=(2, 4)

В группе 35 студентов. Каждый из них изучает хотя бы один иностранный язык (английский или французский). Сколько студентов изучает оба языка, если известно, что английский язык изучают 14 человек, а французский - в два раза больше, чем английский.

Ответ: 7

Найдите пересечение и объединение множеств цифр, используемых в записи чисел 15243 и 6321

Ответ:

А∩В={1,2,3}

АВ={1,2,3,4,5,6}

Пересечением каких множеств является а) множество квадратов?; б) множество прямоугольных равнобедренных треугольников

Выполнить решение с помощью кругов Эйлера.

Ответ: а) множества прямоугольников и множества ромбов;

б) множества прямоугольных треугольников и множества равнобедренных треугольников.

В классе 30 человек. 20 из них каждый день пользуется метро, 15 - автобусом, 23 - троллейбусом, 10 - и метро, и троллейбусом, 12 - и метро, и автобусом, 9 - и троллейбусом, и автобусом. Сколько человек ежедневно пользуются всеми тремя видами транспорта?

Ответ: 3

ТЕХНОЛОГИЧЕСКАЯ КАРТА РАБОТЫ НАД ЗАДАЧЕЙ

Формулировка задачи

В классе 30 человек. 20 из них каждый день пользуется метро, 15 - автобусом, 23 - троллейбусом, 10 - и метро, и троллейбусом, 12 - и метро, и автобусом, 9 - и троллейбусом, и автобусом. Сколько человек ежедневно пользуются всеми тремя видами транспорта.

Решение задачи

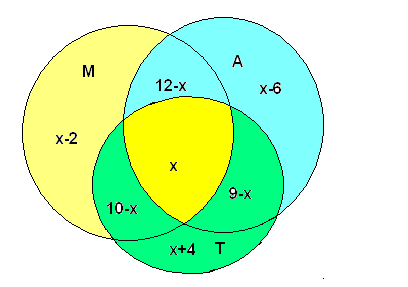
Для решения воспользуемся кругами Эйлера:

Пусть х человек пользуется всеми тремя видами транспорта. Тогда пользуются только метро и троллейбусом - (10 − х) человек, только автобусом и троллейбусом - (9 − х) человек, только метро и автобусом - (12 − х) человек. Найдем, сколько человек пользуется одним только метро:

20 − (12 − х) − (10 − х) − х = х − 2

Аналогично получаем: 15 - (9 - х) - (12 - х) - х = х − 6 - только автобусом и 23 - (10 - х) - (9 - х) - х = х + 4 - только троллейбусом, так как всего 30 человек, составляем уравнение:

Х + (12 − х) + (9 − х) + (10 − х) + (х + 4) + (х − 2) + (х − 6) = 30.

х = 3.

Ответ: 3

Основные этапы работы над задачей

Цель этапа

Содержание педагогического взаимодействия

Деятельность учителя

Деятельность учащихся*

Познавательная

Коммуникативная

Регулятивная

Постановка учебной задачи

Создание проблемной ситуации

Предлагает решить задачу (текст в формулировке задачи)

Организовывает «погружение в проблему».

Фиксируют проблему

Слушают учителя и строят речевое высказывания на уточнение задания

Принимают цель

Совместное исследование проблемы

Поиск способов решения задачи

Задает вопросы

- является ли данная задача задачей на множества?

-Какие основные множества можно выделить по условию задачи?

- Будут ли эти множества независимыми друг от друга?

-что нужно сделать, чтобы ответить на вопрос задачи?

Фиксирует ответы учащихся

Отвечают на вопросы:

-да, т.к. можно выделить множества и в дальнейшем выполнить над ними операции согласно условию задачи.

- {М} - множество учащихся, пользующихся метро, {A} - множество учеников, пользующихся автобусом, {Т} - множество учеников, пользующихся троллейбусом.

- нет, так как в классе есть ученики, которые пользуются двумя и даже тремя видами транспорта.

- Нужно выполнить построение кругов Эйлера для заданных множеств и исследовать построенную графическую модель.

Строят грамотно речевые высказывания, слушают высказывания других учащихся, проводят рефлексию своих действий.

Исследуют условия и способы решения задачи

Моделирование

Создание математической модели

Предлагает выполнить построение кругов Эйлера для установленных множеств таким образом, чтобы они удовлетворяли условию задачи

Предлагает составить модели, для нахождения количества учеников, пользующихся:

только М и А;

только Т и А;

только М и Т;

только М;

только А;

только Т

Как, используя полученные данные, найти сколько всего человек пользуется транспортом?

Строят графическую модель показывают на ней связи между множествами, фиксируют известные данные, и приходят к выводу, что нужно найти пересечение всех трёх выделенных множеств: М, А, Т. Количество элементов которого следует обозначить через х.

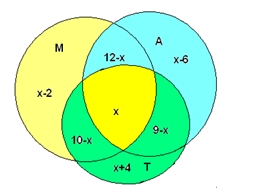
Делают знаково-символическую запись связей и отношений:

Х - кол-во учащихся, пользующихся всеми тремя видами транспорта.

(12 - х) - учеников пользуются только метро и автобусом

(9 - х) - учеников пользуются только троллейбусом и автобусом

(10 - х) - учеников пользуются только метро и троллейбусом

(х - 2) - учеников пользуются только метро;

( х - 6) - учеников пользуются только автобусом;

(х + 4) - учеников пользуются только троллейбусом;

Составляют уравнение:

х + (12 − х) + (9 − х) + (10 − х) + (х + 4) + (х − 2) + (х − 6) = 30

Слушают, воспринимают, записывают высказывания

Осуществляют планирование и самоконтроль

Решение задачи

Нахождение решения задачи

Организует решение полученного уравнения, оценивает правильность решения

Решают полученное уравнение:

х + (12 − х) + (9 − х) + (10 − х) + (х + 4) + (х − 2) + (х − 6) = 30

х + 12 − х + 9 − х + 10 − х + х + 4 + х − 2 + х − 6 = 30

х + 27 = 30

х = 30 - 27

х = 3

Ответ : 3

Планируют учебное сотрудничество

Осуществляют самоконтроль, коррекцию и самооценку

Интерпретация полученного решения

Ответить на поставленный вопрос

Предлагает дать ответ на вопрос задачи

Отвечают на вопрос задачи: три человека ежедневно пользуются всеми тремя видами транспорта.

Слушают, воспринимают, записывают ответ к задаче

Осуществляют самоконтроль, коррекцию и самооценку

Анализ решения

Оценка рациональности решения

Организует обсуждение рациональности решения и оценивание его

Обсуждают и анализируют решение

Слушают, воспринимают высказывания друг друга , выражают свои мысли.

Осуществляют самоконтроль, коррекцию и самооценку

Контроль

Проконтролировать достижение результата

Дает диагностическую работу по вариантам:

1вариант

В группе 35 студентов. Каждый из них изучает хотя бы один иностранный язык (английский или французский). Сколько студентов изучает оба языка, если известно, что английский язык изучают 14 человек, а французский - в два раза больше, чем английский.

2вариант

Некоторые ребята из нашего класса любят ходить в кино. Известно, что 15 ребят смотрели фильм «Обитаемый остров», 11 человек - фильм «Стиляги». Из них 6 смотрели и «Обитаемый остров», и «Стиляги». Сколько человек смотрели только фильм «Стиляги»?

Выполняют работу

Рефлексия своих действий

Осуществляют самоконтроль, коррекцию и самооценку

*В столбце «Деятельность учащегося » описываются показатели, указывающие, что универсальные действия сформированы.

Для перехода к обучению к следующему модулю программы загрузите работу с помощью формы. Для этого перейдите на сайт: infourok.ruи авторизуйтесь. Перейдите в раздел «Мой сайт», далее «Мои курсы» выберите нужный Вам курс и модуль программы. Нажмите кнопку "Загрузить работу" и выберите файл с разработкой на своем компьютере.

Внимание! Разрабатываемые материалы не рецензируются. В названии документа указывайте вид работы и название.

</ Доступные форматы для загрузки: doc, docx.