Урок геометрии по теме: 'Теорема Пифагора' (8 класс)

Характеристики урока

Уровень образования: среднее (полное) общее образование

Класс: 8 класс

Предмет: Геометрия

Тема урока: Теорема Пифагора.

Номер урока: 20

Дата проведения урока: 14.11.2014г.

Цели урока:

общеобразовательные:

• проверить теоретические знания учащихся (свойства прямоугольного треугольника, теорема Пифагора), умение использовать их при решении задач;

• создав проблемную ситуацию, подвести учащихся к "открытию" обратной теоремы Пифагора.

развивающие:

• развитие умений применять теоретические знания на практике;

• развитие умения формулировать выводы при наблюдениях;

• развитие памяти, внимания, наблюдательности:

• развитие мотивации учения через эмоциональное удовлетворение от открытий, через введение элементов истории развития математических понятий.

воспитательные:

• воспитывать устойчивый интерес к предмету через изучение жизнедеятельности Пифагора

Тип урока: урок усвоения новых знаний и умений.

Основной тип обучения: личностно - ориентированное обучение.

Основные виды деятельности: беседа, дискуссия, индивидуальная работа.

Оборудование: компьютер, доска google документ, презентация к уроку, выполненная в Power Point.

Используемые учебники и учебные пособия:

«Геометрия 7-9 классы: учебник для общеобразовательных учреждений, авт. Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, Э.Г. Позняк, И.И. Юдина, 19 издание, М.: Просвещение, 2009. - 384 с

Краткое описание:

Урок геометрии в 8 классе по теме "Теорема Пифагора" - это восьмой урок по теме «Площади», включает в себя повторение теоремы Пифагора, рассмотрение теоремы обратной теореме Пифагора, решение практических задач на применение этих теорем и нахождение площади треугольника.

План урока:

• Организационный момент.

• Актуализация знаний.

• Решение практических задач с использованием теоремы Пифагора.

• Новая тема.

• Первичное закрепление знаний.

• Домашнее задание.

• Итоги урока.

Ход урока

1. Организационная часть.

-Сообщение темы и цели урока.

2. Актуализация знаний. (Демонстрация экрана, работа с презентацией)

Устно ответить на вопросы.

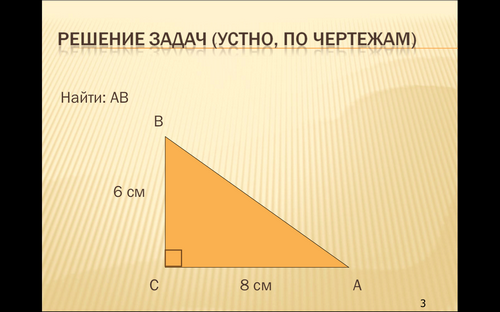
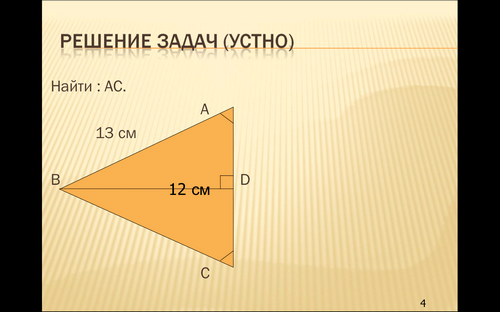
• Перечислите виды треугольников в зависимости от сторон. Слайд 1,2

• Какой треугольник называется прямоугольным?

• Как называются стороны в прямоугольном треугольнике?

• Что такое гипотенуза?

• Как звучит теорема Пифагора?

• Как найти площадь треугольника?

Устно решение задач по слайдам. Слайд 3,4

3. Проверка домашнего задания ( Творческое задание. Просмотр презентации, подготовленной учащимся о Пифагоре и его учениях).

4. Изучение нового материала. (Демонстрация экрана, работа с презентацией)

Устно. Постановка проблемы и ее решение.

(Перед объяснением нового материала необходимо повторить теорему Пифагора. Продолжая формировать навык формулировки обратных утверждений, ученикам предлагается сформулировать теорему, обратную теореме Пифагора, самостоятельно. После формулировки учениками, открывается теорема.)

- Сформулировать утверждения обратные данным и выяснить верные ли они. Слайд 5

- Сформулировать теорему, обратную теореме Пифагора. Слайд 6,7.

- Рассмотреть способ как с помощью веревки и трех колышков построить прямой угол на местности. Слайд 8.

- Рассмотреть Пифагоровы тройки и их особенности. Слайд 9,10.

(Далее в качестве примеров прямоугольных треугольников приводятся пифагоровы треугольники, в которых их стороны целочисленные. Продемонстрировав данные треугольники, выводятся общие правила, как образуются значения сторон таких прямоугольных треугольников. )

- Определить, является ли треугольник прямоугольным, если его стороны выражаются числами. Слайд 11.

5. Закрепление материала. (Работа с виртуальной доской)

Решение задачи.

Дан равнобедренный треугольник с боковой стороной 24 см. И основанием 14 см. Найти высоту и площадь этого треугольника.

6. Итог урока.

- Подведение итогов урока.

- Объявление оценок и домашнего задания.