Конспект урока алгебры в 7 классе 'Разложение многочлена на множители способом группировки'

Урок № __ Класс 7 «__» ____________ 20 __ г.

Тема: Разложение многочлена на множители способом группировки

Тип: урок изучения нового материала

Цели:

• способствовать деятельности учащихся по самостоятельному выводу алгоритма разложения многочлена на множители способом группировки на основании применения переместительного и сочетательного законов сложения и распределительного закона умножения;

• продолжать работу по формированию у каждого учащегося личной потребности в последовательной деятельности, связанной с "открытием" нового правила, развитию творческих способностей учащихся;

• продолжить работу по формированию ответственности учащихся за свою деятельность на уроке, умений самостоятельно добывать знания, овладению способами и критериями самоконтроля и самооценки.

Оборудование:

• учебник «Алгебра, 7 класс» (авторы Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова; под редакцией С.А. Теляковского),

• 12 компьютеров,

• проектор,

• приложение к учебник на электронном носителе.

ПЛАН УРОКА

Этапы урока

Временная реализация

Организационный момент, формулировка темы урока, постановка целей урока

1 мин.

Постановка домашнего задания

1 мин.

Актуализация опорных знаний

5 мин.

Мотивирование необходимости разложения многочлена на множители

5 мин.

Объяснение нового материала

15 мин.

Отработка практических навыков

15 мин.

Подведение итогов урока

2 мин.

ХОД УРОКА

1. Организационный момент.

Приветствие учащихся, проверка присутствующих.

«Привет, друг»

2. Постановка домашнего задания

Изучить п.30, алгоритм, решить № 710, 713 (а), 720(а)

3. Актуализация опорных знаний

I группа - самостоятельная работа в электронном учебнике

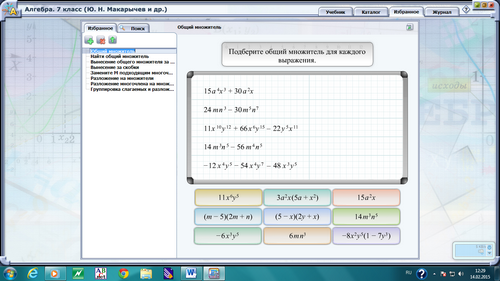
Задание «Найти общий множитель»:

подберите общий множитель для каждого выражения.

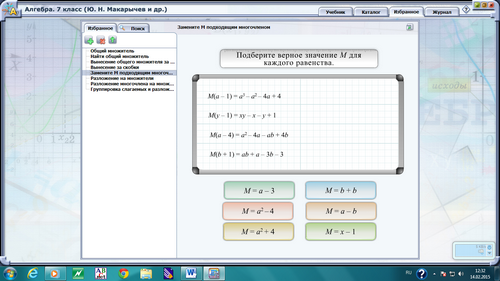
Задание «Замените М подходящим многочленом»: подберите верное значение М для каждого равенства.

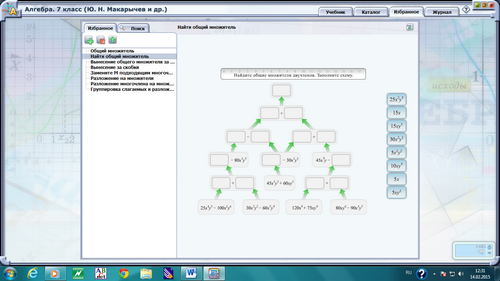
Задание «Найти общий множитель»: найдите общие множители двучленов. Заполните схему.

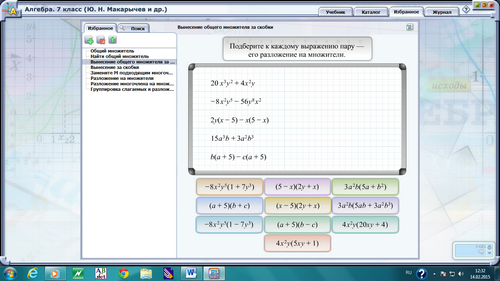
Задание «Вынесение общего множителя за скобки»: подберите к каждому выражению пару - его разложение на множители.

II группа - устная работа под руководством учителя

1. Вынесите за скобки общий множитель:

1. bx+by=b(x+y)

2. (a-c)y-(a-c)z=(a-c)(y-z)

3. (a-b)x+(b-a)y=(a-b)x-(a-b)y=(a-b)(x-y)

2. Разложите на множители:

1. 2a-4a²=2a(1-2a)

3. Представьте в виде произведения:

7a³(x-y)-3b²(y-x)= 7a³(x-y)+3b²(x-y)=(x-y)(7a³+3b²)

4. Вычислите:

9,13 ∙ 4,12 + 4,12 ∙ 0,87=4,12∙(9,13+0,87)=4,12∙10=41,2

Учащиеся возвращаются за свои рабочие места и подключаются к работе.

Учитель: Когда мы выносим общий множитель за скобки, мы представляем многочлен в виде произведения множителей. Для чего это может быть нужно? (Чтобы решить уравнение или сократить дробь).

5. Решите уравнение (запись в тетрадях):

1) 5 x (x+1) =0 , x=0 или x=-1.

2) 6x - 3x² =0 , 3x(2-x) =0 , x=0 или x=2.

4. Мотивирование необходимости разложения многочлена на множители.

Учитель: Решите уравнение: x² +3x +6 +2x =0.

Проблемная ситуация: задача знакома на первый взгляд, но не решается. Мы знаем, что удобно решать уравнение, в правой части которого 0, раскладывая его левую часть на множители.

- Есть ли общий множитель у всех слагаемых? (Нет)

- Значит, этот способ разложения на множители не подходит.

Постановка учебной задачи: научиться раскладывать многочлен на множители другим способом.

Учащиеся записывают в тетрадях тему «Разложение многочлена на множители…» /концовка записывается после «открытия» правила/

5. Объяснение нового материала

1) Эвристическая беседа.

Вопросы учителя

Ответы учащихся

Рассмотрим многочлен

5x +5y +m x +my.

Есть ли общий множитель у всех слагаемых?

Применим "метод пристального взгляда". Что вы увидели?

Есть общий множитель 5 у первого и второго слагаемых и общий множитель m у третьего и четвертого слагаемых.

Давайте объединим их в группы

( 5x +5y ) +(m x +my)

Каким законом сложения воспользуемся?

Сочетательным

Что можно сделать с общим множителем в каждой группе?

Вынести его за скобки

5 (x +y) +m (x +y)

Каким законом умножения воспользуемся?

Распределительным

Сколько сейчас получилось слагаемых?

Два

Что интересного заметили в получившемся выражении?

Есть один общий множитель (х+у)

Вынесем его за скобки

(x +y) (5 +m)

Что мы получили?

Произведение

Значит, многочлен представили в виде произведения. Каким способом?

Объединяя слагаемые в группы

Поэтому этот способ называется способом группировки

2) Самостоятельная работа учащихся, сидящих за первой партой каждого ряда над алгоритмом разложения на множители.

- А сейчас пусть ученики, сидящие за первой партой каждого ряда, составят алгоритм разложения многочлена на множители. /Учащиеся изучают записи в тетрадях/

В это время проводится беседа с остальными:

- Нельзя ли этот же многочлен разложить на множители, группируя слагаемые иначе? Какие законы сложения и умножения будем использовать?

Фронтальная работа с пооперационным контролем:

(5x +5y ) +(m x +my) = x(5 +m) + y (5 +m) =(x +y) (5 +m)

- Какой получился результат? (Такой же, как и в первом случае)

3) Заслушиваются составленные варианты алгоритмов.

Дискуссия, коррекция. Тем самым создается модель алгоритма, ее анализ, уточнение.

Окончательный вариант звучит так:

а) выполнить группировку слагаемых, имеющих общий множитель;

в) отдельно в каждой группе найти общий множитель и вынести его за скобки;

с) в получившемся выражении найти общий множитель и вынести его за скобки.

Этот алгоритм поможет учащимся в дальнейшей работе на этом и последующих уроках.

6. Отработка практических навыков /отработка правила/

Работая с алгоритмом, учащиеся действуют поэтапно, отдавая себе отчет, что надо сделать и почему. Происходит осознание нового правила, его осмысление и запоминание.

а) Фронтальная работа с пооперационным контролем /работа по учебнику/

№ 708, 709 (а,б)

б) Дифференцированные задания по уровням.

Ситуация выбора в процессе выполнения самостоятельной работы. Учащиеся могут выбрать один из предложенных вариантов, который кажется им соответствующим их уровню знаний, то есть вырабатывается навык самооценки.

А. Задания нормативного уровня.

1) 7а-7в+ аn - b n

2) x y+ 2y+2x+4

3) y²a-y²b+x² a- x²b

Б. Задания компетентного уровня

1) x y+ 2y-2x-4

2) 2сх - су - 6х + 3у

3) х² +x y+ xy²+y³

С. Задания творческого уровня

1) x⁴ +x³y- xy³-y⁴

2) ху² - bу² - ах + аb + у² - а

3) х² - 5х + 6

4) .

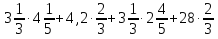VII. Подведение итогов. Рефлексия

1. Решение уравнения

- Какая задача состояла перед нами в начале урока? Можно ли считать, что мы ее решили?

Вернемся к уравнению:

x²+3x+6+2x=0

x(x+3) +2(3+x) =0

(x+3) (x+2) =0

Ответ: х=-3 или х=-2.

2. Совместная работа по электронному учебнику

- Установите порядок разложения на множители каждого из данных многочленов.

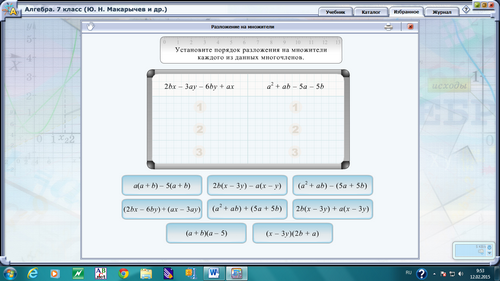
3. Ответы на вопросы:

1) Как умножить многочлен на многочлен?

2) Опишите алгоритм способа группировки разложения на множители.

3) Где применяется способ группировки? /При решении уравнений, вычислительных примеров и текстовых задач/