Урок по алгебре 7 класс по теме «Разложение квадратного трехчлена»

Тема урока:

Разложение квадратного трехчлена на множители.

Цели урока:

1. Добиться от всех учащихся класса успешной отработки и применения знаний при разложении квадратного трехчлена на множители.

2. Способствовать: а) развитию самоконтроля и самообучения;

б) умению пользоваться интерактивной доской;

в) развитию математической грамотности, аккуратности.

3. Воспитывать умение грамотно, лаконично выражать свою мысль, получать удовлетворение от достигнутых результатов.

Тип урока: комбинированный урок с дифференцированным и индивидуальным подходом, с элементами развивающего и опережающего обучения.

Место урока: Второй урок по данной теме (основной), на первых ученики узнали определение квадратного трехчлена, научились находить его корни.

Структура урока:

1. Актуализация знаний с дифференцированным подходом к учащимся.

2. Контроль- самопроверка ранее усвоенных знаний.

3. Поисковый метод.(новая тема)

4. Первичное закрепление изученного, индивидуально - дифференцированный подход.

5. Осмысление, обобщение знаний.

6. Постановка домашнего задания .

Оборудование: интерактивная доска, обычная доска, карточки с заданиями, тесты,дерево с заданиями.

Ход урока

Организационный момент (1 минута).

1. Приветствие учащихся; проверка их готовности к уроку.

2. Сообщение цели урока.

І этап.

«Повторение - мать учения»

. Установите соответствие:

ах²+bх+с; a 0, b 0,c 0

Квадратичная функция

у=ах²+bх+с

Квадратный трехчлен

ах²+bх+с=0, a 0

Полное квадратное уравнение

x²-4=0

Неприведенное неполное уравнение

5х² - х=0

приведенное неполное уравнение

Х⁴-2х²-3=0

Биквадратное уравнение

ІІ этап.

«Доверяй, но проверяй»

Проверочная работа с самоконтролем.

1. Найти корни квадратного трехчлена:

І вариант ІІ вариант

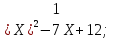1)
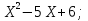
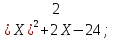2)

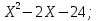
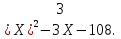
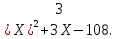
Ответы

к проверочной работе

«Доверяй, но проверяй»

1. Найти корни квадратного трехчлена:

І вариант ІІ вариант

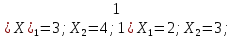
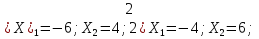
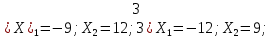
Несколько ярких ответов отметить.

ІІІ этап

«Уменье и труд все перетрут»(10 минут)

1.Раздать карточки с примерами разложений квадратного трехчлена.(рассмотреть примеры,самостоятельно решить третий пример и вывести формулу разложения квадратного трехчлена)

2.Выслушать ответы учащихся.(сравнить правильность с записью на интерактивной доске,записать алгоритм разложения квадратного трехчлена)

IV этап

«Куй железо, пока горячо!»

1.Работа с учебником стр.79 №231(у доски)

2.Вопрос учащимся:

Как вы думаете, где можно применить разложение квадратного трехчлена на множители?

Верно:

при решении уравнений;

при сокращении дробей;

в преобразовании алгебраических выражений.

3. Рассмотрим применение разложения квадратного трехчлена на множители при сокращении дробей. Работа учащихся у доски.

Сократить дробь: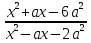

2. А теперь рассмотрим применение разложения квадратного трехчлена на множители в преобразованиях алгебраических выражений.

Учебник. Стр.79 №233

3.Самостоятельная работа

(Дерево с разноцветными листочками:желтые-легкий уровень,зеленый-средний уровень,красный-трудный уровень.)

Подведение итогов урока. Оценивание учащихся.

Рефлексия (3 минуты)

1. Сегодня я узнал…….

2. Было интересно……

3. Было трудно…….

4. Я выполнял задание….

5. Я понял что…….

6. Теперь я могу…….

7. Я почувствовал что…..

8. Я приобрёл….

9. Я научился…….

10. У меня получилось………

11. Я смог….

Информация о домашнем задании: п.12.№235,237

Жетекшинская средняя общеобразовательная школа

Урок по алгебре в 8 Б классе:

Учитель математики :Батурбаева Е.В

2013год

2012год

2012 год.

«Занимательный мир задач»

Внеклассное мероприятие

Цели:

1. Повышение интереса к изучению математики, развитие творческих способностей учащихся, логического мышления.
2. Обучение решению арифметических задач различного типа.
3. Формирование приемов умственной и исследовательской
деятельности.
4. Воспитание интереса к истории математики, навыков учебного
труда.

Оборудование:

название темы мероприятия, таблички с названиями команд и конкурсов, отпечатанные условия задач для конкурсов, плакаты с высказываниями, карточки с задачами для болельщиков, фишки трех цветов.

Плакаты:
1. «Математическая задача иногда столь же
увлекательна, как кроссворд, и напряженная умственная работа
может быть столь же желанным упражнением, как
стремительный теннис». Д.Пойа.
2. «Крупное научное открытие дает решение крупной проблемы,
но и в решении любой задачи присутствует крупица открытия».
Д.Пойа

Ход мероприятия:
I. Организационный момент.
Представление команд.
II. Восьмиклассники читают стихотворение:
Опять ужасная. Опять
В журнале будет двойка.
Слеза стекает на тетрадь,
Нет сил, держаться стойко.
Их целых пять. Их даже - шесть!
Они страшней прививки.
Они мешают спать и есть,
Глотать кефир и сливки.
Как час расплаты настает
Такая вот работа
Холодный прошибает пот
В глазах круги без счета.

III. Ведущий (учитель): Ну хватит, хватит совсем запугали ребят, нагнали на них тоску, это до XVIII века решать задачи было очень сложно, потому что их решали с помощью 30 различных правил, которые надо было знать наизусть, причем обоснование выбора способа их решения не давалось. Ученик должен был заучивать эти правила наизусть и строго придерживаться их при решении заданий. Названия у этих правил тоже являются для нас незнакомыми: фальшивое, тройное, слепое или девичье, аварийное и т.д. Запомнить их все и научиться определять, какое правило, к какой задаче применимо, было очень трудно. С тех пор, видимо, и сложилось у некоторых людей мнение об арифметике как науке сложной и скучной. Но это далеко не так (прочитать высказывание 1).
И мы постараемся это опровергнуть нашим путешествием в занимательный, увлекательный и удивительный мир задач.
IV. Конкур 1:! «Смекалкины обгонялки».
(2 конверта с задачами для команд и 2 конверта с задачами для болельщиков)

Задачи для команд.
1. Женщина обращается к кому-то из вашего класса и говорит «Я тебе мать, но ты мне не сын». Что это значит? (она обращается к девочке)
2. Угадайте слово: «Первое предлог, второе - летний дом. А целое порой решается с трудом?» (Задача)
3. Сколько горошин может войти в пустой стакан? (горошины не ходят)
4. Почему в поездах стоп краны всегда красные, а в самолетах голубые? (в самолетах нет стоп-крана)
5. Сколько земли в дыре глубиной 2 метра, шириной 2 метра, длиной 2 метра? (нисколько)
6. Выходили 12 молодцев, выносили 52 сокола, выпускали 365 лебедей, (год, месяцы, дни).
7. Один человек купил трех коз и заплатил 3 рубля. Спрашивается: по чему пошла каждая коза? (козы по деньгам не ходят)
8. Математическое отношение: чем больше из нее берешь, тем больше она
становится? (яма)
9. Петух, стоя, на одной ноге, весит 5 кг. Сколько он будет весить, если
встанет на обе? (5 кг)
10. Увеличьте число 666 в полтора раза, не производя над этим числом никаких арифметических действий. (перевернуть число)

Задача для болельщиков.
По дороге вдоль кустов
Шло 11 хвостов. Сосчитать я также смог,
Что шагало 30 ног. Это вместе шли куда-то,
Петухи и поросята.
И вопрос мой к вам таков:
Сколько было петухов? ( 7 петухов)

V. Конкурс 2: «Логический Фейерверк». (На доске оформлен фейерверк с разноцветными кружочками, на которых написаны числа, соответствующие № задач)
1. У одного старика спросили, сколько ему лет. Он ответил, что ему сто лет и несколько месяцев, но дней рождения у него было всего 25. как же это могло быть? (этот человек родился 29 февраля и день рождения у него бывает один раз в 4 года)
2. Ослица и мул шли вместе, нагруженные мешками равной массы. Ослица жаловалась на тяжесть ноши. «Чего ты жалуешься? - сказал мул. - Если ты дашь мне один свой мешок, моя ноша станет вдвое больше твоей, а если я дам тебе один свой мешок, то наши грузы только сравнятся». Сколько мешков было у каждого? (7 и 5 мешков)
3. Двое ели сливы. Один сказал другому: «Дай мне свои две сливы, тогда слив у нас будет поровну». На что другой ответил: «Нет, лучше ты дай мне свои две сливы, тогда у меня будет в два раза больше, чему тебя». Сколько слив было у каждого? (8 и 12)
4. Возраст дедушки выражается наименьшим трехзначным числом, которое записывается различными числами. Сколько лет дедушке? (102 года)
5. По Шотландии в одном купе поезда едут два пассажира. Один из них поглядев в окно, удивился:
- Смотрите! - воскликнул он. В Шотландии оказывается овцы черные!
- Отнюдь, - ответил попутчик.- В Шотландии есть хотя бы одна овца, у которой хотя бы один бок черный. Кто из них лучше знает математику?(Второй)

VI.Конкурс 3: «Математический ералаш».
1. Собственная скорость катера 11 км/ч. Скорость течения реки 2 км/ч. Какой путь пройдет катер за 4 часа против течения реки?(3 7 км)
2. В библиотеке 4600 книг. Книг на иностранном языке 18% всего количества, остальные книги на русском языке. Сколько в библиотеке книг на русском языке? (3772 книги)
3. Сахарный песок при переработке в рафинад теряет своего веса. Сколько надо взять сахарного песка, чтобы получилось 104 кг рафинада? (120 кг)
4. В карьере добыто 150 тонн руды, которая содержит железа, а остальное - пустая порода. Сколько железа и пустой породы в этой руде? (108 кг железа, 42 кг породы)
5. Отец старше сына в 3 раза, или на 34 года. Каков возраст отца и сына? (17 лет сыну, 51 год отцу)

VII.Конкурс 4: «Исторический звездопад». (Задачи оформлены на звёздочках, с одной стороны которых наклеены портреты известных людей, а с другой - тексты их задач. Если участники команд смогут назвать фамилию исторической личности, то они получают дополнительные баллы.
Задачи взяты из учебника математики 5-6 класса под редакцией Петерсона)
а) Задача Толстого.
б) Задача Ньютона.
в) Задача Магницкого.
г) Задача Пифагора.
д) Задача Пуассона.

VIII. Конкурс 5: «А вам слабо?»
Задача Дидоны.
Финикийская царевна Дидона, спасаясь от своего брата, тирана Пигмалиона, отплыла из родного города Тира с небольшим отрядом своих сторонников. Было это, если верить легенде, около 825 года до нашей эры. Долго плыли царевна и ее спутники по Средиземному морю, пока не пристали к берегу Африки. Жили в тех местах нулидийцы. Пришельцы им были совершенно ни к чему. Но Дидоне некуда было деться, место ей понравилось, и царевна стала упрашивать нулидийского царя Ярба продать ей немного земли. Желая, видимо, отделаться от назойливой финикиянки, Ярб заломил баснословную цену за клочок земли, который можно окружить одной бычьей шкурой. К его удивлению и разочарованию, Дидона приняла это издевательское предложение, расплатилась и отправилась отмерить свою землю. Только она не стала расстилать шкуру на берегу. Как она это сделала?(Учащимся предлагается макет бычьей шкуры, вырезанный из альбомного листа бумаги и ножницы)
(Ответ: Сначала она разрезала ее так, что получила тонкий кожаный ремешок (а он вышел очень длинный), и этим ремешком окружила солидный участок, на котором и основала в последствии великий город Карфаген. Ярб был в ярости: так, как его, мало кого одурачивали за всю историю человечества. Но он был честным человеком и сдержал слово: земля осталась за Дидоной. Так это было или не так - теперь судить трудно. Но, между прочим, карфагенская цитадель называлась Бирса, что и значит «бычья шкура»
Итак, задача, которую пришлось решить Дидоне, такова: какую наибольшую площадь можно окружить веревкой заданной длины? Или, иначе: какая геометрическая фигура среди фигур с одинаковым периметром имеет наибольшую площадь? (оказывается, круг)

IX.Конкурс: «Домашнее задание».
Каждая команда готовит дома задачу в рисунке (на ватмане) и задает ее другой команде.
X.Подведение итогов. (Независимые наблюдатели считают количество набранных баллов).
1) грамоты
2) призы
Концовка: прочитать 2 высказывания и слова:
Конкурс сегодня завершен,
Но каждый должен знать:
Познание, упорство, труд
К прогрессу в жизни приведут!

1

вопросы

2

по вертикали: 1)геометрическая фигура,имеющая три

стороны и три угла.

по горизонтали: 2) отношение противолежащего катета к

3

прилежащему; 3) отношение противолежащего катета к

гипотенузе; 4) отношение прилежащего катета к противо -

4

лежащему; 5) отношение прилежащего катета к гипотенузе;

6) сторона треугольника, прилежащая к прямому углу.

6

1

вопросы

2

по вертикали: 1)геометрическая фигура,имеющая три

стороны и три угла.

по горизонтали: 2) отношение противолежащего катета к

3

прилежащему; 3) отношение противолежащего катета к

гипотенузе; 4) отношение прилежащего катета к противо -

4

лежащему; 5) отношение прилежащего катета к гипотенузе;

6) сторона треугольника, прилежащая к прямому углу.

6