Урок по математике Решение логарифмических уравнений и неравенств(10 класс)

Предмет: Алгебра и начала анализа

Тема урока: Решение логарифмических уравнений и неравенств

Форма урока: комбинированный урок

Тип урока: Урок повторного контроля знаний. Обобщение и закрепление пройденного материала.

Цели урока:

1.Обучающая - вторичное осмысление уже известных знаний, выработка умений и навыков по их применению. Закрепить основные методы решения логарифмических уравнений, предупредить появление типичных ошибок.

2.Развивающая - развитие логического мышления для сознательного восприятия учебного материала, внимание, зрительную память, активность учащихся на уроке. Предоставить каждому из учащихся проверить свой уровень подготовки по данной теме.

3.Воспитывающая - воспитание познавательной активности, формирование личностных качеств: точность и ясность словесного выражения мысли; сосредоточенность и внимание; настойчивость и ответственность, положительной мотивации к изучению предмета, аккуратности, добросовестности и чувство ответственности. Осуществить индивидуальный подход и педагогическую поддержку каждого ученика через задания и благоприятную психологическую атмосферу.

Задачи урока:

• выработать у учащихся умение пользоваться алгоритмом решения логарифмических уравнений.

• осуществить формирование первоначальных знаний в виде отдельных навыков после определенной тренировки решения уравнений.

• использовать авторскую презентацию для зрительного восприятия

Методы и педагогические приемы:

Методы самообучения

Приемы устного опроса.

Приемы письменного контроля.

Коллективная учебная деятельность.

Раздаточный материал: задания для работы в группах

Ход урока:

I.Орг.момент( приветствие, отметка отсутствующих)

II.Объявление темы и целей урока:

Для определения ключевого слова, входящего в название темы выполните кроссворд: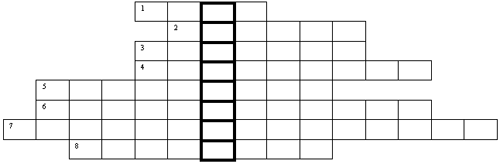

Вопросы кроссворда :

На что нельзя делить? (ноль)

Как называется ответ при решении уравнения? (корень)

Часть математики, в которой рассматриваются решения уравнений. (алгебра)

Равенство с переменной (уравнение)

Равенство двух отношений (пропорция)

От чего зависит количество корней квадратного уравнения? (дискриминант)

Как называется функция вида у = log_ax ? (логарифмическая)

Как называется независимая переменная? (аргумент)

Ключевое слово - ЛОГАРИФМ.

III. Актуализация опорных знаний учащихся:

1) Устный опрос по теории :

1.Что значит решить уравнение?

2.Что такое корень уравнения?

3.Какие уравнения называют логарифмическим?

4. Что называется логарифмом? Десятичным логарифмом?

5. Какие свойства логарифмов вы знаете?

6. Какая функция называется логарифмической? Область определения и область значения.

7. Когда логарифмическая функция убывает, когда возрастает на всей области определения?

8.Какие методы решения логарифмических уравнений вы уже рассматривали на уроках алгебры ?

2) Математический диктант:

Вопросы - задания.

На которые ученик отвечает «да» или «нет»

1. Логарифмическая функция y=log_а x определена при любом х.(-)

2. Функция y=logax логарифмическая при a>0, a=0, x>0.(+)

3. Область определения логарифмической функции является множество действительных чисел.(-)

4. Область значений логарифмической функции является множество действительных чисел.(+)

5. Логарифмическая функция - четная.(-)

6. Логарифмическая функция - нечетная.(-)

7. Функция y=log₃ x - возрастающая.(+)

8. Функция y=logax при 0

9. График логарифмической функции всегда находится в I и IV четвертях.(+)

10. График логарифмической функции всегда пересекает Ох в точке (1;0).(+)

11. Существует логарифм отрицательного числа.(-)

12. Существует логарифм дробного положительного числа.(+)

+- вопросы 2, 4,7,9,10,12

3) Вычислить значения логарифмов: ( задания по рядам)

2) log ₂ 16; log ₂ 64; log ₂ 2;

log ₂ 1 ; log ₂ (1/2); log ₂ (1/8);

log ₃ 27; log ₃ 81; log ₃ 3;

log ₃ 1; log ₃ (1/9); log ₃ (1/3);

log_1/2 1/32; log_1/2 4; log_0,5 0,125;

log_0/5 (1/2); log_0,5 1; log_1/2 2.

IV. Формирование практических умений и навыков:(работа в группах)

А)Логарифмический марафон, последующая взаимопроверка в группах

</<font size="3">С помощью

определения

Потенциирование

Введение

новой переменной

1

-1; 2

+

2

log₃ (x² - 3x - 5) = log₃ (7 - 2x).

-3

+

3

lg ² x - lg x - 6 = 0.

0,01; 1000

+

4

log_ах=log_а10- log_а2

5

+

5

lg(х-9)+ lg(2х-1)=2

13

+

6

lоg₂ ² x - lоg₂ x - 2 = 0.

¼ ; 4

+

7

log_0,6 (7x - 21) > log_0,6 6х

( -∞; 21)

8

log

(12; ∞)

Б) Изучение нового :

Решить систему уравнений : ( домашняя заготовка)

Ответ: (6;8) или (8;6)

V. Из истории логарифмов.

Изобретение логарифмов в начале XVII века тесно связано с развитием производства и торговли, астрономии и мореплавания, требовавших усовершенствования методов вычислительной математики. Все чаще требовалось быстро производить громоздкие действия над многозначными числами, все точнее и точнее должны были быть результаты вычислений. Вот тогда-то и нашла воплощение идея логарифмов, ценность которых состоит в сведении сложных действий III ступени ( возведения в степень и извлечения корня) к более простым действиям II ступени (умножению и делению), а последних-

к самым простым, к действиям I ступени (сложению и вычитанию).

Изобретение логарифмов, название их и первые таблицы логарифмов принадлежат шотландскому любителю математики Джону Неперу (1550 -1617), хотя раньше его составил первые таблицы логарифмов также любитель математики - часовщик и мастер астрономических приборов швейцарец И. Бюрги. Однако таблицы Бюрги были опубликованы в 1620 г., а таблицы Непера появились в 1614 г. Составлением логарифмических таблиц эти талантливые люди занимались параллельно, но независимо один от другого. При составлении таблиц оба они руководствовались идеей, высказанной еще Архимедом, а затем более подробно исследованной М. Штифелем в работе " Полная арифметика" .

Разработка идеи Архимеда и Штифеля приводит к понятию логарифма. Из различных систем логарифмов замечательны две: логарифмы с иррациональным основание е = 2,7182818284…, которые носят название натуральных, и системы логарифмов с основанием 10, называемые десятичными логарифмами.

VI. Караоке

Группам одновременно предлагается решить уравнения и про полученное в ответе число напеть строчку из песни, где оно встречается.

1. log _1/2x = -1 (х=2, «Дважды два - четыре, дважды два - четыре…»)

2. log _3/3x = -2 (х=3, «Три танкиста, три веселых друга, экипаж машины боевой…»)

3. lg x = 6 (х=1000000, «Миллион, миллион алых роз…»)

4. log ₂x = -1 (х=0,5, «Половинку сердца оставлю с тобою…», «Полчаса без тебя, полчаса…»)

5. log ₂₀₀₆x = 0 (х=1, «Ты единственная моя…»)

VII. Рефлексия.

В качестве рефлексии всем учащимся предлагается написать синквейн: 3 существительных, которые отвечают внутреннему состоянию учащегося, такие же 3 глагола, 3 прилагательных, 1 слово с «!» на конце и законченное предложение. Подведение итогов.

Учитель делает вывод о степени достижимости поставленных в начале урока целей и благодарит учащихся за работу на уроке.

VIII. Домашнее задание: п.39, № 529(а),521(б,г)