- Учителю
- Дидактический материал для проведения дифференцированных работ на уроках математики в 5-6 классах
Дидактический материал для проведения дифференцированных работ на уроках математики в 5-6 классах
МБОУ «Филипповская основная общеобразовательная школа»
«Создание системы дидактического материала для проведения дифференцированных работ на уроках математики в 5 и 6 классах».
Выполнила
учитель
математики
Емельянова Л.В.
апрель 2012 год
Страшная это опасность - безделье,
безделье за партой, безделье шесть
часов подряд ежедневно, безделье
месяцы и годы. Это развращает,
морально калечит человека, и ни
школьная бригада, ни школьный
участок, ни мастерская - ничто не
может возместить того, что
упущено в самой главной сфере,
где человек должен быть
тружеником, - в сфере мысли.
В.А.Сухомлинский
Идея дифференцированного обучения является отнюдь не новой для нашей отечественной школы. Система образования в России стала складываться при Петре I. Он наметил основной путь - путь создания широкой сети общеобразовательных школ, специальных школ и училищ. В России стали создаваться школы различной практической направленности, готовящие учащихся к различным профессиям. Обучение в средних учебных заведениях носило элементы дифференцированного характера. Основанием для дифференциации были не только потребности общества в различных профессиях, но и индивидуальные особенности, интересы школьников. В начале ХIХ века была создана новая система образования. В ней предусматривались следующие четыре ступени:
высшая - университеты;
средние - гимназии;
промежуточная - уездные училища;
низшая - приходские училища.
Именно в гимназиях разрешалось увеличивать число учебных предметов, когда находились способные к тому или иному предмету дети. Можно считать, что это было первым прообразом такой формы дифференцированного обучения, как факультативные занятия или занятия по выбору. Ученый и педагог К.П.Яновский (1822 - 1902) писал: «Важный момент в обучении - это выявление способностей учащихся и создание необходимой для их дальнейшего развития среды». В феврале 1988 года состоялся Пленум ЦК КПСС, посвященный вопросам образования, на котором был рассмотрен комплекс мер по обновлению школы. В частности, был принят тезис о необходимости дифференцированного обучения, направленного на развитие индивидуальных особенностей учащихся.
Еще Ушинский писал, что ребенок от природы не имеет душевной лености, он любит деятельность, хочет все делать сам. Нет детей, ни к чему не способных. Способности можно развить, не развить или пригасить. Можно целенаправленно способствовать развитию всех детей и индивидуально каждого, и одним из наиболее эффективных способов является дифференцированное обучение, которое особенно необходимо в сельской школе. В наше время открываются физико-математические классы и школы, что позволяет углубленно изучать математику, но это характерно для городов и крупных населенных пунктов. В сельской школе обычно наполняемость классов очень мала. В одном классе обучаются учащиеся с очень разными способностями и их стремления, как правило, не совпадают. Где же выход?
Неоспорим тот факт, что обучение математике - это искусство, направленное не на весь класс одновременно, а на каждого ученика в отдельности. Но не все дети одинаково трудолюбивы. Один умен, да ленив - махнет рукой на предстоящий путь к знаниям, да повернет назад. Другой, наоборот, испытывает радость от приобщения к творчеству. Ну, а третий? А третьему в жизни здорово не повезло. По разным причинам: бывает, что не повезло с родителями, с товарищами, или учительница первая читать и считать детей научила, а вот играть ей с ними, в глаза заглянуть некогда было. Вот и сидит теперь этот третий тихонько на уроке и очень хочет, чтобы его не беспокоили никакими премудростями. Да и по своим природным способностям, уровню восприятия, темпу работы, специфике мыслительной деятельности учащиеся заметно отличаются друг от друга. В данной ситуации учитель чаще всего выбирает формы и методы обучения, направленные на достижение результатов средним учеником. При таком отношении сильные ученики теряют интерес к учению, а слабые - ищут обходные пути: механическое заучивание, списывание. Поэтому задача учителя математики - раскрыть индивидуальные способности каждого ученика, чтобы на уроке активизировать, стимулировать и направлять процесс мышления всех детей.
Для того, чтобы на уроке максимально развить каждого ученика я создала дидактический материал для проведения дифференцированных работ на уроках математики в 5 - 6 классах.
Важным моментом дифференциации обучения является размещение детей в классе в зависимости от вида работы: а) по одному; б) по парам; в) по группам; г) по вариантам; д) по «творческим союзам».
Можно выделить три группы учащихся с различными математическими способностями:
Группа А - учащиеся, имеющие хорошие математические способности;
Группа В - учащиеся, имеющие средние математические способности;
Группа С - учащиеся, имеющие низкие математические способности.
Подбор системы задач и упражнений по темам является самой трудоемкой работой. При организации базового повторения задания выбираю так: первое задание составляется, чтобы проверить усвоение решения «опорных задач»; второе - добавляются некоторые элементы сложности; третье - аналогично второму, только его сложность еще чуть увеличена; четвертое задание - повышенной сложности, требующее дополнительных знаний, смекалки, неординарного мышления. Зачетные, самостоятельные работы и контрольные работы провожу также дифференцированно. Самостоятельные работы обычно разделяю на три вида: решение по образцу (для группы С); выбор верного ответа из нескольких предложенных (для группы В); самостоятельное решение более сложных заданий (для группы А). Как показал опыт работы, внедряемые элементы дифференцированного подхода активизируют стремление детей к знаниям. Ученики чувствуют себя ответственными за процесс обучения, приучаются к организации учебного труда.

2. На сколько изменится семизначное число, оканчивающееся на 40, если эти две цифры поменять местами?
3. Выполните действия: 52 998 : (37 + 29).
2. Тема «Числовые и буквенные выражения»
Группа С: 1. Упростите выражения: а) 28 - (15 + с); б) а - 64 - 26;
в) (154 + а) - 24; г) 137 - с - 27.
Решение: а) 28 - (15 + с) = 28 - 15 - с = 13 - с;
б) а - 64 - 26 = а - (64 + 26) = а - 90;
в) (154 + а) - 24 = (154 - 24) + а = 130 + а;
г) 137 - с - 27 = 137 - (с + 27) = 137 - (27 + с) =
= 137 - 27 - с = 110 - с.
2. Решите уравнения: а) (х + 98) + 14 = 169; б) (35 + у) - 15 = 31.
Решение: а) х + 98 = 169 - 14 б) 35 + у = 31 + 15
х + 98 = 155 35 + у = 46
х = 155 - 98 у = 46 - 35
х = 57 у = 11
Реши сам:
1. Упростите выражения: а) 35 - (18 + у); б) а - 128 - 472;
в) (248 + у) - 24; г) 384 - с - 137.
2. Решите уравнения: а) (х + 15) - 8 = 17; б) (24 + х) + 21 = 56.
Группа В: 1. Упростите выражения: а) а - 28 - 37;
1) а - 9; 2) а - 65; 3) 65 + а.
б) (12 - х) + 24;
1) х - 12; 2)12 - х; 3) 36 - х.
2. Решите уравнения: а) (у - 35) + 12 = 32;
1) 55; 2) 15; 3) 79.
б) 56 - (х + 12) = 24.
1) 68; 2) 20; 3) 44.
Группа А: 1. Найдите значение выражения, предварительно упростив его:
а) 149 + у - 99 при у = 77; б) 237 + с + 163 при с = 194.
2. Решите уравнения: а) (45 - у) + 18 = 58; б) 55 - (х - 15) = 30.
3. Тема «Упрощение выражений»
Группа С: 1. Упростите выражение: а) 23а + 37а; б) 48х + х; в) 27р - 18р.
Решение: а) 23а + 37а = (23 + 37)а = 60а;
б) 48х + х = (48 + 1)х = 49х;
в) 27р - 18р = (27 - 18)р = 9р.
2. Найдите значение выражения: 38а + 62а, если а = 238.
Решение: 38а + 62а = (38 + 62)а = 100а = 100 · 238 = 23 800, если а = 238
3. Решите уравнение: 15у - 8у = 714.
Решение: 15у - 8у = 714
(15 - 8)у = 714
7у = 714
у = 714 : 7
у = 102
Реши сам:
1. Упростите выражение: а) 4у + 36у; б) а + 56а; в) 84х - 78х.
2. Найдите значение выражения: 375у - 175у при у = 48.
3. Решите уравнение: 9х + х = 500.
Группа В: 1. Упростите выражение: а) 32х - х; б) 32х + 64х; в) 15у - 5х.
1) 31х, 32х, 20у; 2) 31х, 96х, 10у; 3) 33х, 106х, 5у.
2.Найдите значение выражения: 32х + 68х, если х = 24.
1) 2 400, 2) 240, 3) 24.
3. Решите уравнение: 10k - k = 702.
1) 87, 2) 78, 3) 66.
Группа А: 1. Упростите выражение: а) 3а + 17 + 3а + 14; б) k + 35 + 4k + 26.
2. Найдите значение выражения: 11m - 11n, если m = 308, n = 208.
3. Решите уравнение: 6t + 3t - t = 6 400.
4. Тема «Степень числа»
Группа С: 1. Представьте в виде степени произведение:
а) 6 · 6 · 6 · 6 · 6 · 6 · 6; Решение: а) 67;
б) 25 · 25 · 25 · 25 · 25; б) 255;
в) 73 · 73; в) 732;
г) х · х · х · х; г) х4;
д) z · z · z. д) z3.
2. Представьте в виде произведения степень:
а) 75; Решение: а) 7 · 7 · 7 · 7 · 7;
б) 124; б) 12 · 12 · 12 · 12;
в) х3; в) х · х · х.
3. Найдите значение выражения: а) 5 + 42; б) 7 + 33; в) 24 + 32.
Решение: а) 5 + 4 · 4 = 5 + 16 = 21;
б) 7 + 3 · 3 · 3 = 7 + 27 = 3
в) 2 ·2 · 2 · 2 + 3 · 3 = 16 + 9 = 25.
Реши сам:
1. Представьте в виде степени: а) 11 · 11 · 11 ·11; б) 9 · 9 · 9;
в) а · а · а · а ·а; г) у · у.
2. Представь те в виде произведения степень:
а) 153; б) 605; в) а8.
3. Найдите значение выражения: а) 52 + 42; б) 73 + 4; в) 63 + 24.
Группа В: 1. Найдите значения: 24; 33; 105.
1) 8, 9, 50; 2) 6, 9, 55; 3) 16, 27, 100 000.
2. Найдите значение выражения: а) 92 + 19; б) 172 - 209; в) 34 · 104.
1) 100, 185, 120 000; 2) 100, 80, 810 000; 3) 37, 80, 8 100.
Группа А: 1. Найдите значение: 182; 53; 402; 303; 112.
2. Найдите значение выражения: а) 63 : 3;
б) (15 - 7)2 : 23;
в) 106 - 204..
5. Тема «Площади и объемы»
Группа С: 1. Найти площадь прямоугольника, длина которого равна 5 см, а ширина - 2 см.
Решение: S = a · b, а - длина, b - ширина
S = 5 · 2 = 10 (см2)
2. Найдите площадь квадрата со стороной 15 см.
Решение: S = a2, а - сторона квадрата
S = 152 = 15 · 15 = 225 (см2)
3. Найдите объем прямоугольного параллелепипеда, если его длина равна 10 см, ширина - 6 см , высота - 5 см.
Решение: V = a · b · c, а - длина, b - ширина, с - высота
V = 10 · 6 · 5 = 300 (см3)
Реши сам:
1. Найти площадь прямоугольника, если его длина равна 7 см, а ширина - 5 см.
2. Найти площадь квадрата со стороной 11 см.
3. Найдите объем прямоугольного параллелепипеда, если его длина равна 8 см, ширина - 4 см, высота - 5 см.
Группа В: 1. Длина прямоугольника равна 28 см, а его ширина в 7 раз меньше. Чему равна площадь прямоугольника?
а) 196 см2, б) 4 см2, в) 112 см2.
2. Чему равна сторона квадрата, если его площадь 36 см2?
а) 18 см, б) 6 см, в) 9 см.
3. Высота комнаты 3 м, ширина 5 м и длина 6 м. Сколько кубических метров воздуха находится в комнате?
а) 90 м3, б) 14 м3, в) 30 м3.
Группа А: 1. Два прямоугольника имеют равные площади. Длина первого прямоугольника 16 см, а его ширина на 12 см меньше длины. Длина второго прямоугольника 32 см. Найдите ширину второго прямоугольника.
2. Сарай, имеющий форму прямоугольного параллелепипеда, заполнен сеном. Длина сарая 10 м, ширина 6 м, высота 4 м. Найдите массу сена в сарае, если масса 10 м3 сена равна 6 ц.
6. Тема «Сложение и вычитание дробей с одинаковыми знаменателями»
Группа С: 1. Выполните действие: а) 4/7 + 2/7; б) 7/9 - 2/9;
в) 13 /19 + 5/13; г) 37/100 - 16/100.
Решение: а) 4/7 + 2/7 = (4 + 2)/7 = 6/7
б) 7/9 - 2/9 = (7 - 2)/9 = 5/9
в) 13/19 + 5/19 = (13 + 5)/19 = 18/19
г) 37/100 - 16/100 = (37 - 16)/100 = 21/100
2. Найдите значение выражения: а) 4/11 + а, если а = 1/11;
б) b - 1/10, если b = 7/10.
Решение: а) 4/11 + 1/11 = (4 + 1)/11 = 5/11, если а = 1/11;
б) 7/10 - 1/10 = (7 - 1)/10 = 6/10, если b = 7/10.
3. Решите уравнение: х - 5/12 = 2/12.
Решение: х - 5/12 = 2/12
х = 2/12 + 5/12
х = (2 + 5)/12
х = 7/12
Реши сам:
1. Выполните действия: а) 1/9 + 6/9; б) 4/5 - 3/5;
в) 13/100 + 26/100; г) 12/17 - 3/17.
2. Найдите значение выражения: а) 3/14 + с, если с = 1/14;
б) d - 3/17, если d = 5/17.
3. Решите уравнение: у - 7/19 = 11/19.
Группа В: 1.Выполните действия: а) 18/19 - 7/19 + 3/19; б) 2/7 + 4/7 - 5/7;
в) 9/11 - 3/11 - 2/11; г) 11/15 - (3/15 + 7/15).
1) 8/19, 1/7, 4/11, 14/15; 2) 14/19, 1/7, 4/11, 1/15;
3) 14/19, 6/7, 8/11, 13/15.
2. Решите уравнение: а) 15/16 - у = 3/16; б) 7/25 + р = 18/25.
1) 18/16, 1/25; 2) 12/16, 11/25; 3) 18/32, 1/50.
Группа А: 1. Выполните действия: а) 3/9 + 2/9 - 4/9; б) 5/18 + 12/18 - 9/18;
в) 12/19 - 1/19 - 5/19; г) 25/23 - 10/23 + 3/23.
2. Решите уравнение: а) 17/20 - х = 14/20 - 3/20;
б) 8/15 - 7/15 + у = 14/15.
7. Тема «Сложение и вычитание десятичных дробей»
Г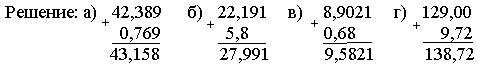
руппа С: 1. Выполните сложение: а) 0,769 + 42,389; б) 5,8 + 22,191;
в) 8,9021 + 0,68; г) 129 + 9,72.
2. Выполните вычитание: а) 9,4 - 7,3; б) 88,252 - 4,69;
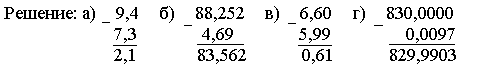
в) 6,6 - 5,99; г) 830 - 0,0097.
3. На пальто израсходовали 3,2 м ткани, а на костюм - 2,63 м. Сколько ткани израсходовали на пальто и костюм вместе?
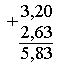
Решение: 1) 3,2 + 2,63 = 5,83(м)
Ответ: на пальто и костюм израсходовали 5,83 м ткани.
Реши сам:
1. Выполните сложение: а) 7,8 + 6,9; б) 95,381 + 3,219;
б) 24,2 + 0,867; г) 425 + 2,647.
2. Выполните вычитание: а) 7,79 - 3,79; б) 8,1 - 5,46;
в) 425 - 2,647; г) 37,2 - 0,03.
3. Масса Автомобиля «Нива» 11,5 ц, а масса автомобиля «Волга» 14,2 ц. На сколько масса «Волги» больше массы «Нивы»?
Группа В: 1. Выполните действия: а) 9,83 - 1,76; б) 8,93 + 1,212;
в) 14 - 3,96; г) 83 + 5,46.
1) 8,07; 10,142; 10,04; 88,46. 2) 10,57; 20,42; 3,82; 5,99;
3) 8,07; 9,305; 4,1; 6,92.
2. Решите уравнение: а) х + 3,8 = 8; б) у - 6,5 = 12.
1) 11,8; 5,5; 2) 4,2; 18,5; 3) 4,6; 6,62.
3, С одного участка собрали 95,37 т зерна, а с другого - на 16,8 т больше. Сколько тонн зерна собрали с двух участков?
1) 112,17 т; 2) 97,05 т; 3) 207,54 т.
Группа А: 1. Выполните действия: а) 12,371 - 8,93 + 1,212;
б) 14 - (3,96 + 7,85).
2. Решите уравнение: а) 2,8 + х + 3,7 = 12,5; б) (5,6 - у) + 3,8 = 4,4.
3. Найдите периметр треугольника АВС, если АВ = 2,8 см, ВС больше АВ на 0,8 см, но меньше АС на 1,1 см.
8. Тема «Округление чисел»
Группа С: 1. Округлите дроби: а) 2,781; 3,1423 до десятых;
б) 0,07268; 1,35506 до сотых;
в) 167,1; 444,4 до десятков.
Решение: а) 2,7`81 » 2,8, т.к. после 7 стоит 8, а 8 > 5, то к 7 прибавляем 1, остальные цифры отбрасываем;
3,1`423 » 3,1, т.к. после 1 стоит 4, а 4 < 5, то просто отбрасываем оставшиеся цифры;
б) 0,07`268 » 0,07, т.к. после 7 стоит 2,а 2 < 5, то просто отбрасываем оставшиеся цифры;
1,35`506 » 1,36, т.к. после 5 стоит 5, а 5 = 5, то к 5 прибавляем 1, а остальные цифры отбрасываем;
в) 16`7,1 » 170, т.к. после 6 стоит 7, а 7 > 5, то к 6 прибавляем 1, а оставшуюся в целой части цифру заменяем нулем;
44`4,4 » 440, т.к. после 4 стоит 4, а 4 < 5, то оставшуюся в целой части цифру заменяем нулем;
2. Трасса лыжных гонок состоит из 4 участков. Первый участок имеет длину 4,35 км, второй - 5,75 км, третий - 6,95 км и четвертый - 2,8 км. Найдите длину всей трассы и округлите ответ до целых километров.
Решение: 4,35 + 5,75+ 6,95 + 2,8 = 19,85(км)
19`,85 » 20, т.к. после 9 стоит 8 ,а 8 > 5, то к 9 прибавляем 1, а остальные цифры отбрасываем.
Ответ: длина всей трассы 20 километров.
Реши сам:
1. Округлите дроби: а) 0,3691; 0,8218 до десятых;
б) 10,081; 4,455 до сотых;
в) 2085,04; 300,7 до десятков.
2. Одна деталь имеет массу 13,26 кг, вторая - 14,43 кг, третья - 1,66 кг, а четвертая - 15,875 кг. Найдите общую массу этих деталей и округлите результат до десятых долей килограмма.
Группа В: 1. Округлите дроби: а) 203,935; 80,46 до десятых;
1) 203,9; 80,4; 2) 204; 80,5; 3) 203,9; 80,5;
б) 10,081; 4,455 до сотых;
1) 10,08; 4,46; 2) 10,1; 4,45; 3) 10,09; 4,50;
в) 2085,04; 300,7 до десятков.
1) 2080; 300; 2) 2090; 300; 3) 2081; 301.
2. Старинная русская мера массы пуд равна 16,38 кг. Округлите это значение до целых. Старинная русская мера длины верста равна 1067 м. Округлите это значение до сотен. Старинная русская мера длины сажень равна 2,13 м. Округлите это значение до десятых.
1) 16; 1100; 2,1; 2) 16,1; 1000; 2,4; 3) 17; 1060; 2,2.
Группа А: 1. Округлите дроби:
а) 1,69; 1,198; 37,444; 37,5444; 802,3022 до целых;
б) 0,3691; 0,8218; 0,9702; 81,3501 до десятых.
2. Найдите периметр четырехугольника АВСD, если АВ = 6,2 дм, СD больше АВ на 3,14 дм, но меньше ВС на 2,31 дм; АD больше ВС на 1,2 дм. Ответ округлите: а) до десятых долей дециметра;
б) до целых дециметров.
9. Тема «Умножение и деление десятичных дробей»
Группа С: 1. Выполните умножение: а) 6,25 · 4,8; б) 74 · 4,9; в) 1,15 · 0,07;
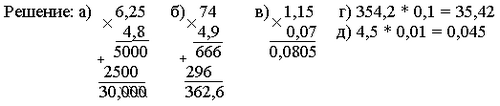
г) 354,2 · 0,1; д) 4,5 · 0,01.
2. Выполните деление: а) 7,56 : 0,6; б) 0,468 : 0,09; в) 636 : 0,12;
г) 5,453 : 0,01; д) 7,8 : 0,001.
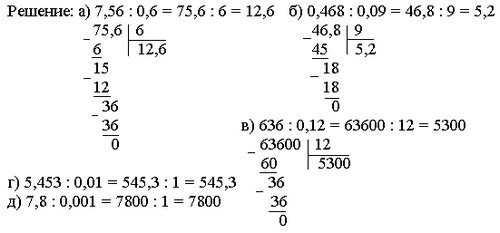
Реши сам:
1. Выполните умножение: а) 85,8 · 3,2; б) 82 · 0,92; в) 3,43 · 4,8;
г) 248,34 · 0,1; д) 378,82 · 0,001.
2. Выполните деление: а) 10,5 : 3,5; б) 0,824 : 0,8;
в) 46,08 : 0,384; г) 7,54 : 0,1; д) 4 : 0,01.
Группа В: 1. Выполните умножение: а) 0,25 · 0,48; б) 8,4 · 18,5;
в) 12,6 · 7,8; г) 37 · 0,0001; д) 5,4 · 0,01.
1) 12; 15,54; 9,828; 0,37; 0,54; 2) 1,2; 1,554; 982,8; 3,7; 54;
3) 0,12; 155,4; 98,28; 0,0037; 0,054.
2. Выполните деление: а)0,00261 : 0,03; б) 6,944 : 3,2;
в) 16,1 : 0,7; г) 0,8939 : 0,1; д) 0,0102 : 0,001.
1) 0,87; 21,7; 2,3; 89,39; 1,02; 2) 0,087; 2,17; 23; 8,939; 10,2;
3) 0,0087; 0,217; 0,23; 893,9; 102.
Группа А: 1. Длина школьного коридора 30,24 м, а ширина 5,12 м. Найдите его площадь в квадратных метрах.
Ответ округлите до сотых.
2. Путь от дома до школы равен 1,1 км. Девочка проходит этот путь за 0,25 ч. С какой скоростью идет девочка?
3. Выполните действия: (21,2544 : 0,9 + 1,02 · 3,2) : 5,6.
10. Тема «Проценты»
Группа С: 1. Запишите в виде десятичной дроби: 1%, 6%, 123%.
Решение: 1% = 1 : 100 = 0,01; 6% = 6 : 100 = 0,06;
123% = 123 : 100 = 1,23
2. Запишите в процентах десятичную дробь: 0,87; 0,07; 1,45.
Решение: 0,87 · 100 = 87%; 0,07 · 100 = 7%; 1,45 · 100 = 145%.
3. На поле, площадь которого 620 га, работали хлопкоуборочные машины. За сутки они убрали 15% всего поля. Сколько гектаров хлопка убрали за сутки?
Решение: 15% = 0,15
620 · 0,15 = 93 (га)
Ответ: за сутки убрали 93 гектара хлопка.
Реши сам:
1. Запиши в виде десятичной дроби: 8%; 45%; 250%.
2. Запишите в процентах десятичные дроби: 0,035; 2,67; 0,53.
3. Бригаде поручили отремонтировать участок дороги длиной
760 м. Сколько метров дороги бригада отремонтирует, когда выполнит 30% задания?
Группа С: 1. Ученик прочитал 138 страниц, что составляет 23% числа всех страниц в книге. Сколько страниц в книге?
Решение: 23% = 0,23
138 : 0,23 = 600 (стр.)
Ответ: в книге 600 страниц.
2. В школе 700 учащихся. Среди них 357 мальчиков. Сколько процентов учащихся этой школы составляют мальчики?
Решение: 357 : 700 = 0,51
0,51 · 100 = 51%
Ответ: мальчики составляют 51% всех учащихся этой школы.
Реши сам:
1. Площадь одной комнаты 12 м2, и она составляет 25% площади всей квартиры. Найдите площадь всей квартиры.
2. Фрекен Бок испекла 80 пирожков, и Карлсон тут же съел 10 пирожков. Сколько процентов всех пирожков съел Карлсон?
Группа В: 1. В палатку завезли 850 кг огурцов. Первый покупатель взял для соления 1% всех огурцов, а второй - 3% всех огурцов. Сколько килограммов огурцов купил каждый из них?
1) 85 кг; 255 кг; 2) 0,85 кг; 2,55 кг; 3) 8,5 кг; 25,5 кг.
2. Масса медвежонка составляет 15% массы белого медведя. Найдите массу белого медведя, если масса медвежонка 120 кг.
1) 18 кг; 2) 800 кг; 3) 1200 кг.
3. Из 200 арбузов 16 оказались незрелыми. Сколько процентов всех арбузов составили незрелые арбузы?
1) 8%; 2) 1250%; 3) 32%.
Группа А: 1. Геологи проделали путь длиной 2450 км. 10% пути они пролетели на самолете, 60% пути проплыли в лодках, а остальную часть прошли пешком. Сколько километров геологи прошли пешком?
2. Засеяли 24% поля. Осталось засеять 45,6 га этого поля. Найдите площадь всего поля.
3. В классе 17 мальчиков, а девочек на 6 больше. Сколько процентов класса составляют девочки и сколько процентов класса составляют мальчики?
6 класс
Самостоятельные работы
1. Тема «Делимость чисел»
Г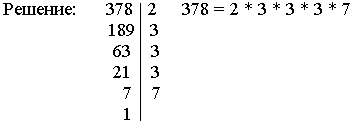
руппа С: 1. Разложите на простые множители число 378.
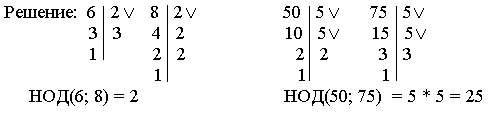
2. Найти НОД чисел 6 и 8, 50 и 75.
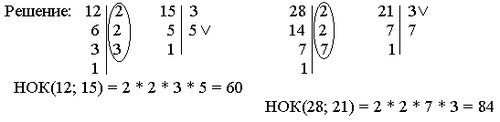
3. Найти НОК чисел 12 и 15, 28 и 21.
Реши сам:
1. Разложите на простые множители число 180.
2. Найти НОД чисел 35 и 88.
3. Найти НОК чисел 72 и 99.
Группа В: 1. Разложите на простые множители число 180.
1) 4, 9, 5; 2) 2, 2, 5, 3, 3; 3) 6, 6, 5.
2. Найти НОД чисел 123 и 82.
1) 3; 2) 246; 3) 41.
3. Найти НОК чисел 48 и 40.
1) 8; 2) 240; 3) 120.
Группа А: 1. Разложите на простые множители число 2052.
2. Найти НОД и НОК чисел 1584 и 2376.
3. Докажите, что числа а) 512 и 234 не взаимно простые;
б) 25 и 64 взаимно простые.
2. Тема «Пропорции»
Группа С: 1. Решите уравнение: 1,3 : 3,9 = х : 0,6.
Решение: х = (1,3 · 0,6) : 3,9
х = 7,8 : 3,9
х = 2

2. Для приготовления 8 одинаковых приборов требуется 12 кг цветных металлов. Сколько кг цветных металлов потребуется для изготовления 6 таких приборов?
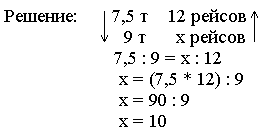
3. Для перевозки груза автомашине грузоподъемностью 7,5 т пришлось сделать 12 рейсов. Сколько рейсов придется сделать автомашине грузоподъемностью 9 т для перевозки этого же груза?
Ответ: придется сделать 10 рейсов.
Реши сам:
1. Решите уравнение 7,2 : 2,4 = 0,9 : х.
2. Из 12 кг пластмассы получают 32 одинаковые трубы. Сколько таких труб получится из 9 кг пластмассы?
3. Производительность первого станка- автомата - 15 деталей в минуту, а второго - 12 деталей в минуту. Чтобы выполнить заказ, первому станку потребовалось 3,6 мин. Сколько минут потребуется второму станку на выполнение этого же заказа?
Группа В: 1. Решите уравнение 1,6 : х = 2,4 : 4,5.
1) 0,9; 2) 0,3; 3) 3.
2. Из 300 кг молока получают 63 кг сливок. Сколько необходимо взять молока, чтобы получить 84 кг сливок?
1) 350; 2) 400; 3) 450.
3. 16 рабочих выполняют некоторое задание за 12 часов. За какое время выполняют это задание 4 рабочих с той же производительностью труда?
1) 48; 2) 3; 3) 24.
Группа А: 1. Решите уравнение х : 0,1 = 14 : 4,9.
2. Для отопления здания заготовлено угля на 180 дней при норме расхода 0,6 т угля в день. На сколько дней хватит этого запаса, если его расходовать ежедневно по 0,5 т?
3. На 20 км пути машина расходует 3 1/5 литра бензина. Сколько бензина машина израсходует на 50 км пути?
3. Тема «Положительные и отрицательные числа»
Группа С: 1. Отметьте на координатной прямой точки А(3), В(- 4),
С(- 4,5), Д(5,5), Е(- 3). Какие из отмеченных точек имеют противоположные координаты?
Решение:
Противоположные координаты у точек А и Е, т.к. они отличаются только знаком. | 3 | = | - 3 |.
2. Сравните: а) - 1,5 и - 1,05; б) - 2,8 и 2,7; в) 3/4 и 2/3.
Решение: а) - 1,5 < - 1,05, т.к. | - 1,5| > | - 1,05 |;
б) - 2,8 < 2,7, т.к. 2,7 - положительное число, а - 2,8 - отрицательное число;
в) 3/4 > 2/3, т.к. 3/4 = 9/12, а 2/3 = 8/12, 9/12 > 8/12.
3. Найдите значение выражения: а) | - 3,8 | : | - 19 |;
б) | - 1 2/7 | · | 4 2/3 |; в) | 3,5 | + | - 1 1/2|.
Решение: а) | - 3,8 | : | - 19 | = 3,8 : 19 = 0,2;
б) | - 1 2/7 | · | 4 2/3 | = 1 2/7 · 4 2/3 = 9/7 · 14/3 = 126/21 = 6;
в) | 3,5 | + | - 1 1/2 | = 3,5 + 1 1/2 = 3,5 + 1,5 = 5.
Реши сам:
1. Отметьте на координатной прямой точки М(- 7), N(4), К(3,5),
Р(- 3,5), S(- 1). Какие из отмеченных точек имеют противоположные координаты?
2. Сравните: а) - 3,7 и 3,6; б) - 8,3 и - 8,03; в) - 4/5 и - 5/6.
3. Найдите значение выражения: а) | 5,4 | : | - 27 |;
б) | - 1 3/8 | · | - 2 2/11|; в) | 3,8 | - | - 2 1/2|.
Группа В: 1. Запишите в порядке возрастания числа:
- 5,2; 3,7; - 6,8; - 3,4;2,2; - 0,7.
1) - 0,7; - 3,4; - 5,2; - 6,8; 2,2; 3,7;
2) - 6,8; - 5,2; - 3,4; - 0,7; 2,2; 3,7;
3) - 0,7; 2,2; - 3,4; 3,7; - 5,2; - 6,8.
2. Сравните числа: а) - 5,8 и 4,5; б) - 12,6 и - 12,8;
в) - 7/18 и - 5/12.
1) а) - 5,8 > 4,5; б) - 12,6 < - 12,8; в) - 7/18 < - 5/12;
2) а) - 5,8 < 4,5; б) - 12,6 > - 12,8; в) - 7/18 > - 5/12;
3) а) - 5,8 < 4,5; б) - 12,6 > - 12,8; в) - 7/18 < - 5/12.
3. Вычислите: а) |8/9| + |- 4/15|; б) |- 4 5/8| - |- 2 1/12|;
в) |- 38,16| : |3,6|.
1) 1 7/45; 2 13/24; 10,6; 2) 7/45; 13/24; - 10,6; 3) 28/45; - 6 17/24; 1,6.
Группа А: 1. Отметьте на координатной прямой числа, удовлетворяющие неравенству 2,3 < х < 7.
2. Решите уравнение: а) |х| = 7,6; б) |х| = - 5; в) - х = 8;
г) - х = - 2.
3. Найдите значение выражения: а) | 5,4 | : | - 27 |;
б) | - 1 3/8 | · | - 2 2/11|; в) | 3,8 | - | - 2 1/2|.
4. Тема «Сложение и вычитание положительных и отрицательных чисел»
Группа С: 1. Найдите значение выражения: а) - 3,8 - 5,7; б) - 8,4 + 3,7;
в) 3,9 - 8,4; г) - 2,9 + 7,3; д) - 2/9 + 5/8; е) - 1 3/4 - 2 1/12.
Решение: а) - 3,8 - 5,7 = - 3,8 + (- 5,7) = - (3,8 + 5,7) = - 9,5;
б) - 8,4 + 3,7 = - (8,4 - 3,7) = - 4,7;
в) 3,9 - 8,4 = 3,9 + (- 8,4) = - (8,4 - 3,9) = - 4,5;
г) - 2,9 + 7,3 = 7,3 - 2,9 = 4,4;
д) - 2/9 + 5/8 = - 16/72 + 45/72 = 45/72 - 16/72 = 29/72;
е) - 1 3/4 - 2 1/12 = - 1 3/4 + (- 2 1/12) = - (1 3/4 + 2 1/12) = - (1 9/12 + 2 1/12) = - 3 10/12 = - 3 5/6.
2. Найдите расстояние между точками А(- 2,8) и В(3,7) на координатной прямой.
Решение: АВ = 3,7 - (- 2,8) = 3,7 + 2,8 = 6,5
Реши сам:
1. Найдите значение выражения: а) - 2,9 - 3,6; б) - 3,5 + 8,1;
в) 4,5 - 8,3; г) - 7,5 + 2,8; д) - 5/6 + 3/8; е) - 2 5/7 - 1 3/14.
2. Найдите расстояние между точками С(- 4,7) и Д(- 0,8) на координатной прямой.
Группа В: 1. Вычислите: а) - 7,4 + 3,9; б) 6,7 + (- 5,4); в) - 3,8 + (- 4,2);
г) - 5/6 + 3/8; д) - 4,7 - (- 8,2); е) 3,4 - (- 12,8);
ж) 6,7 - 10; з) - 2,4 - 5,9.
1) 11,3; 12,1; 8; 21/24; 3,5; 9,4; 3,3; 2,5;
2) - 3,5; 1,3; - 8; - 11/24; 3,5; 16,2; - 3,3; - 8,3.
3) 3,5;- 1,3; 8; 11/24;- 3,5;- 16,2; 3,3; 8,3.
2. Решите уравнение: а) 8,6 + х = 5,1; б) у - 5 3/4 = - 6 5/8.
1) 3,5; 1 2/4; 2) - 3,5; 1 1/8; 3) 3,5; - 7/8.
Группа А: 1. Найдите значение выражения
(6/35 - 4/7) - (- 1,8 - 4,3) - 5,7.
2. Решите уравнение: а) 5,23 + х = - 7,24;
б) у - 2 5/12 = 8 - 3 7/15.
5. Тема «Умножение и деление рациональных чисел»
Группа С: 1. Выполните действия: а) 49 · (- 14); б) - 4,2 · (- 0,7);
в) - 1 1/14 · 2 1/3; г) 56 : (- 8); д) - 7,5 : (- 0,5); е) - 4/7 : (- 8/21).
Решение: а) 49 · (- 14) = - 686; б) - 4,2 · (- 0,7) = 2,94;
в) - 1 1/14 · 2 1/3 = - 15/14 · 7/3 = - 5/2 = - 2 1/2;
г) 56 : (- 8) = - 7; д) - 7,5 : (- 0,5) = 15;
е) - 4/7 : (- 8/21) = 4/7 · 21/8 = 3/2 = 1 1/2.
2. Вычислите 0,9 · (4/5 · (- 0,2) - 21/25).
Решение: 0,9 · (4/5 · (- 0,2) - 21/25) = - 0,9
1) 4/5 · (- 0,2) = 4/5 · (- 2/10) = - 8/50;
2) - 8/50 - 21/25 = - 8/50 - 42/50 = - 50/50 = - 1;
3) 0,9 · (- 1) = - 0,9.
Реши сам:
1. Выполните действия: а) 91 · (- 24); б) - 6,3 · (- 0,9);
в) - 8 1/13 · 1 1/26; г) 54 : (- 9); д) - 10,5 : (- 0,3);
е) 24/25 : (- 12).
2. Вычислите 16,09 - (- 8,4) · (- 7/12) - (- 3,7)2.
Группа В: 1. Выполните действия: а) 1,6 · (- 4,5); б) - 135,2 : (- 6,5);
в) - 1 7/8 · 1 1/3; г) 1 2/3 : (- 3 1/3).
1) 7,2; - 20,8; 2 1/2; 1/2; 2)- 7,2; 20,8;- 2 1/2; - 1/2;
3) 7,1; 19,7; 1 7/24; - 3 3/9.
2. Решите уравнение (6х - 9)(4х + 0,7) = 0.
1) 1,5; 0,175; 2) - 1,5; - 0,175; 3) 1,5; - 0,175.
Группа А: 1. Найдите значение выражения 3/7 · (- 0,54) - 1,56 · 3/7.
2. Решите уравнение (- 4х - 3)(3х + 0,6) = 0.
3. Найдите значение выражения
- 7/12 · n - 1, если n = - 1; 3/7.
6. Тема «Подобные слагаемые»
Группа С: 1. Приведите подобные слагаемые: а) - 16 + 16у + 12 - 12у;
б) 6х - 22 - 20 + 15х; в) - 48а + 6 - 6а + 14;
г) 14х - 21 + 12х - 8.
Решение: а) - 16 + 16у + 12 - 12у = 4у - 4 ;
б) 6х - 22 - 20 + 15х = 21х - 42;
в) - 48а + 6 - 6а + 14 = - 54а + 20;
г) 14х - 21 + 12х - 8 = 26х - 29.
2. Решите уравнение: 6х + 24 - 5х - 2 = 0.
Решение: 6х + 24 - 5х - 2 = 0
х + 22 = 0
х = - 22
Реши сам:
1. Приведите подобные слагаемые: а) - 8х + 16 - 15х + 3;
б) 7а - 56 - 78 + 11а; в) - 24у + 5 - 7у + 61;
г) 32х - 43 + 42х - 9.
2. Решите уравнение: 7х + 27 - 6х - 45 = 0.
Группа В: 1. Приведите подобные слагаемые: а) 2ху - 7 - 4ху + 9;
б) 5(6х - 5) + 3(2х - 2); в) 2/7(14а - 7/2b) - 12(5/6а - 6b).
1) - 2ху + 2; 36х - 31; - 6а + 71b;
2) 2ху - 2; 8х - 7; 14а - 73b;
3) 6ху - 16; 33х + 27; 88а + 73b.
2. Раскройте скобки и найдите значение выражения
23,6 + (14,5 - 30,1) - (6,8 + 1,9).
1) 16,7; 2) - 0,7; 3) 74.
3. Решите уравнение: - 9а + 10а = - 2 - 8.
1) 6/19; 2) - 10; 3) - 6.
Группа А: 1. Раскройте скобки и найдите значение выражения
17,8 - (11,7 + 14,8) - (3,5 - 12,6).
2. Упростите выражение 4/9(2,7m - 2 1/4n) - 4,2(5/7m - 0,5n).
3. Решите уравнение 0,3(х - 2) - 0,2(х + 4) = 0,6.
7. Тема «Решение уравнений»
Группа С: 1. Решите уравнение: а) 4х + 12х = 3х + 8;
б) 3х - 17 = 8х + 18;
в) 0,18у - 3,54 = 0,19у - 2,89; г) 4(3 - х) - 11 = 7(2х - 5).
Решение: а) 4х + 12х = 3х + 8 б) 3х - 17 = 8х + 18
4х + 12х - 3х = 8 3х - 8х = 17 + 18
13х = 8 - 5х = 35
х = 8 : 13 х = 35 : (- 5)
х = 8/13 х = - 7
в) 0,18у - 3,54 = 0,19у - 2,89 г) 4(3 - х) - 11 = 7(2х - 5)
0,18у - 0,19у = 3,54 - 2,89 12 - 4х - 11 = 14х - 35
- 0,01у = 0,65 - 4х - 14х = - 12 + 11 - 35
у = 0,65 : (- 0,01) - 18х = - 36
у = - 65 х = - 36 : (- 18)
х = 2
2. За 1,8 кг огурцов и 2,4 кг помидоров заплатили 216 руб. Известно, что 1 кг помидоров дороже 1 кг огурцов на 20 руб. Сколько стоит 1 кг помидоров?
Решение: Пусть х руб стоит 1 кг огурцов, тогда (х + 20) руб. стоит 1 кг помидоров. По условию задачи сказано, что за 1,8 кг огурцов и 2,4 кг помидоров заплатили 216 руб.
Составим уравнение: 1,8х + 2,4(х + 20) = 216
1,8х + 2,4х + 48 = 216
4,2х = 216 - 48
4,2х = 168
х = 168 : 4,2
х = 40
х + 20 = 40 + 20 = 60 (кг)
Ответ: 1 кг помидоров стоит 60 рублей.
Реши сам:
1. Решите уравнение: а) 7у - 11 = 10у + 16;
б) 5х + 27 = 4х + 21;
в) 0,87а - 0,9а + 1,3а = - 15,24; г) 0,4(6х - 7) = 0,5(3х + 7).
2. За арбуз в 4,2 кг и дыню в 5,4 кг заплатили 396 руб. Известно, что 1 кг дыни дороже 1 кг арбуза на 20 руб. Сколько стоит 1 кг дыни?
Группа В: 1. Решите уравнение: а) 5,6 + 0,6х = 0,3х - 1,3;
б) 8х - 25 = 3х + 30;
в) - 3,2n + 4,8 = - 2,4n + 4,8; г) 0,4(6х - 7) = 0,5(3х + 7).
1) 23; - 11; 1; 9; 2) - 23; 11; 0; 7; 3) 32; 5; 10; 63.
2. На первой стоянке в 4 раза меньше автомашин, чем на второй. После того как на первую приехало 35 машин, а со второй уехало 25 машин, на стоянках стало поровну. Сколько машин было на каждой стоянке первоначально?
1) 12; 48; 2) 3; 12; 3) 20; 80.
Группа А: 1. Решите уравнение: а) 0,6(х + 7) = 0,5(х - 3) + 6,8;
![]()
2. Сумма двух чисел равна 48. Найдите эти числа, если 40% одного из них равно 2/3 другого.
3. Найдите два корня уравнения | - 0,63| : |х| = | - 0,9|.
Литература:
1. Исторические аспекты дифференциации обучения, И. Смирнова, газета «Математика», №44, 2000г;
2. Технология дифференцированного обучения в условиях сельской школы,
Л. Егошина, газета «Математика», №14, 2008 г;
3. О дифференцированном обучении и стратовой системе, Н. Куликова, газета «Математика», №17, 2008 г;
4. Учебник «Математика - 5», Н.Я. Виленкин, изд. «Мнемозина», М., 2008 г;
5. Учебник «Математика - 6», Н.Я. Виленкин, изд. «Мнемозина», М., 2008 г;
6. Уроки математики в 6-м классе, С.В. Замуреева, «Феникс», Ростов-на-Дону, 2003 г.
7. Поурочные разработки по математике, 5 класс, П.П.Попова, «Вако», М., 2008 г.