Урок-практикум по геометрии в 11 классе 'Объёмы тел вращения'.

Урок-практикум на тему: «Объемы тел вращения».

Тип урока: урок применения знаний.

Цель: изготовление фигур вращения - цилиндра и конуса, измерение величин, характеризующих их размеры.

Задачи урока:

образовательная - систематизация и коррекция знаний учащихся по пройденной теме, применение этих знаний для решения практических задач;

развивающая - развитие пространственного мышления при решении задач, развитие умений сопоставлять, измерять параметры геометрических фигур;

воспитательная - воспитание таких качеств личности как внимательность, аккуратность, самостоятельность, объективность в самооценке результатов работы.

Методы: учебная дискуссия; самостоятельная работа; проектирование; анализ конкретных ситуаций; коллективная мыслительная деятельность.

Оборудование: модели фигур вращения, задания для каждого учащегося, цветной картон, циркули, транспортиры, ножницы, клей, скотч.

Структура урока.

1. Организационный момент.

2. Актуализация знаний.

3. Практическая работа.

4. Итог урока.

5. Домашнее задание.

Организационный момент постановка целей урока.

Первый этап работы - актуализация знаний. Повторение теоретического материала и взаимопроверка степени его усвоения, а также уровня готовности перехода к практической части.

Перечень вопросов:

Назовите тела вращения, которые вы знаете?

Выберите из представленных фигур прямой круговой цилиндр.

Выберите из представленных фигур прямой круговой конус.

Покажите на выбранной фигуре её боковую поверхность и основания.

Диктант:

1. 1.Что представляет собой осевое сечение цилиндра?

2. Может ли осевым сечением являться квадрат? Если да, то, в каком случае?

3. Чему равна площадь прямоугольника?

4. Чему равна площадь квадрата?

5. Чему равна площадь круга?

6. Как найти длину окружности?

7. Что представляет собой сечение цилиндра плоскостью, параллельной основанию?

8. Что представляет собой осевое сечение конуса?

9. Что представляет собой боковая поверхность конуса в развёртке?

10. Может ли осевым сечением конуса быть равносторонний треугольник? Если да, то, в каком случае?

11. Может ли осевым сечением конуса являться прямоугольный треугольник? Если, да, в каком случае?

12. Чему равна площадь равностороннего треугольника?

13. Чему равна площадь прямоугольного треугольника?

14. Чему равна площадь основания конуса?

15. Запишите формулу объёма цилиндра.

16. Запишите формулу объёма конуса.

Проводится взаимопроверка. Учащиеся меняются заданиями попарно:

Учащиеся в ходе дискуссии обсуждают ответы, исправляют ошибки и выставляют оценки за теоретические вопросы. Потом учащиеся приступают к выполнению практических заданий.

Второй этап урока - практическая работа. Каждый учащийся получает задачу практической направленности. Учащиеся могут обсуждать порядок выполнения работы. Дифференциация практического задания заключается в следующем:

а) можно самостоятельно сделать развёртку фигуры, произвести все измерения, вычислить заданные величины, затем изготовить соответствующую фигуру вращения;

б) можно самостоятельно сделать развёртку фигуры, произвести все измерения, вычислить заданные величины;

в) можно заранее подготовить развёртки фигур вращения, чтобы учащиеся занимались только измерениями и расчетами.

Учащимся предоставляется право выбора задания.

Первое задание. Цилиндр.

Вырезать из плотного цветного картона прямоугольник произвольного размера. Изготовить основания и сделать цилиндр.

Найти:

1) высоту цилиндра;

2) радиус основания;

3) площадь основания;

4) площадь боковой поверхности;

5) площадь полной поверхности;

6) объём цилиндра.

Второе задание. Конус.

Начертить круг произвольного радиуса, вырезать сектор. Изготовить основание. Сделать конус.

Найти:

1) площадь сектора;

2) радиус основания;

3) площадь основания;

4) площадь боковой поверхности;

5) площадь полной поверхности;

6) объём конуса.

Алгоритм выполнения практической работы (используется учителем для координации действий учащихся и для проверки правильности вычислений).

Первое задание. Цилиндр.

На листе картона начертить прямоугольник. Измерить стороны: а =…, b = ….

Вырезать прямоугольник.

Чтобы изготовить основание цилиндра, нужно знать его радиус. Известная длина прямоугольника - а, это не что иное, как длина окружности С = 2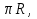 отсюда радиус основания - R = .

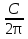Высота цилиндра - вторая сторона прямоугольника, т.е. h = b.

Площадь основания - S_осн. = 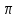R².

Площадь боковой поверхности - S_{бок.пов.} = ab = hС.

Площадь полной поверхности - S_{полн.пов.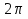} = R² + ab.

Объём цилиндра - V = S_осн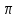.h = R²h .

Второе задание. Конус.

Начертить круг произвольного радиуса, вырезать сектор. С помощью транспортира измерить его угол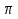

Площадь сектора - S = 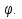, где радиус окружности.

Радиус основания - это радиус окружности полученной из дуги сектора - С =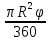 r =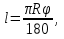

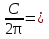
Площадь основания - S_осн. = 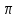r².

Площадь боковой поверхности - это площадь сектора, которая уже определена или - S_{бок.пов.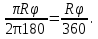} = где 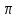образующая конуса (радиус сектора).

Площадь полной поверхности - S_{полн.пов.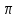} = r² +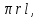

Объём конуса - V = 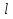S_осн.h, высоту определить путём измерения.

Заключительный этап работы.

Рефлексия. Продолжить предложения:

Больше всего на уроке мне понравилось…

Я хорошо научился…

У меня пока не получается…

Мне ещё надо выучить…

Я оцениваю свою работу на уроке на…

Оценка работы: оценка выставляется каждому ученику по результату работы за урок, за теоретическую и практическую часть, учитывая самостоятельность выполнения работы. Учитель комментирует оценки.

Домашнее задание: повторение формул площадей и объёмов фигур вращения.