Урок Свойства функции: промежутки знакопостоянства (10 класс)

Алгебра 10 класс.

Тема: «Свойства функции: промежутки знакопостоянства».

Тип урока: изучение новой темы

Цель урока:

1. Рассмотреть свойство функции «Промежутки знакопостоянства», и обобщить все изученные свойства.

2. Развитие умения определять промежутки знакопостоянства функции, заданной графически или аналитически.

3. Воспитание коммуникабельности, умения сотрудничать в группе.

Оборудование: ИД+ презентация, раздаточный материал.

Ход урока:Приветствие.

Психологический настрой.

Актуализация опорных знаний:

1.Что такое функция?

2.Какими свойствами обладает функция?

3.Что такое область определения (множество значений) функции?

4.Как вы понимаете четность и нечетность функции? ФОВ?

5.Приведите пример периодичной функции.

6.Промежутки возрастания, убывания, Экстремумы функции.

Эти свойства мы можем прочитать по графику функции

Называют друг другу прилагательное-комплимент.

Отвечают на вопросы, дополняют ответы.

II. Самостоятельная работа. 5 мин

Презентация «Чтение свойств функции по ее графику» Работа в парах (5 баллов).

Выход на тему, по слайду №2.

Строит подмостки для выхода на тему.

В противном случае называет тему и цели урока.

Выполняют задания, проверяют каждое задание в парах.

Тема: «Промежутки знакопостоянства функции».

Цель урока: Рассмотреть свойство функции: «Промежутки знакопостоянства», определять промежутки знакопостоянства функции, заданной графически и аналитически.

III. Работа в группах. 15 мин

Организует заполнение оценочных листов.

Организует деление на группы.

Раздает задания группам.

Теоретическая часть задания командам: Работа с учебником на стр 27. Определение «Промежутков знакопостоянства функции» способ их нахождения,

1)если функция задана графически. Нули функции.

2)если функция задана аналитически (пример 1)

3)если функция задана аналитически (пример 2)

Практическая часть задания командам:

1) №59 (а), 2) №59 (б), №59 (в).

Творческая часть: Каждая функция имеет свой паспорт. В этом паспорте есть личные данные функции, но нет изображения функции. Составьте «портрет функции» по ее свойствам. (приложение 1)

Подводят итоги самостоятельной работы. (Оценочные листы). Три ученика, набравшие самое большое количество баллов делят класс на 3 группы.

Работают в группах по теоретической части. Оформление постера и выступление команд.

Работают в группах по практической части.Выступление команд.

Работают в группах по творческой части.

Выступление команд. Оценивают другие группы цветными стикерами.

IV.Тестирование. 5 мин

Организует тестирование.

Определяет время.

Проводит обмен листами.

Организует проверку тестов по кодам.

Ответы к тесту 1 вариант:Ответы к тесту 2 вариант: Учащиеся получают карточки с тестами на 2 варианта. Ответы отмечают в тестах (приложение 2)

Группы обмениваются листами и проверяют по кодам.

V. Подведение итога урока.5 мин

Организует заполнение оценочных листов.

Заполняют оценочные листы. Выставляют оценки

VI. Домашнее задание. 3 мин

Теоретический материал стр 27.

№56, №63

Записывают

VII. Рефлексия.

2 мин

Прикрепляет к доске пословицы. «Как пришло, так и ушло»

«За один раз дерево не срубишь»

«Усердие все превозмогает»

Предлагает выбрать пословицу, соответствующую его настроению в конце урока.

Каждый приклеивает свой стикер на данную пословицу.

Оценочный лист .

работа (презентация) 0-5 балл.

Работа в группе

(за активность)

0-3 баллов

Выступление у доски.

0-3 баллов

Тестирование

0-6 баллов

Оценка за урок.

15-… «5»

12-14 «4»

9-11 «3»

баллы

Приложение 1

Нарисуйте «портрет» функции, используя ее свойства:

1. Это четная функция

2. Ее область определения

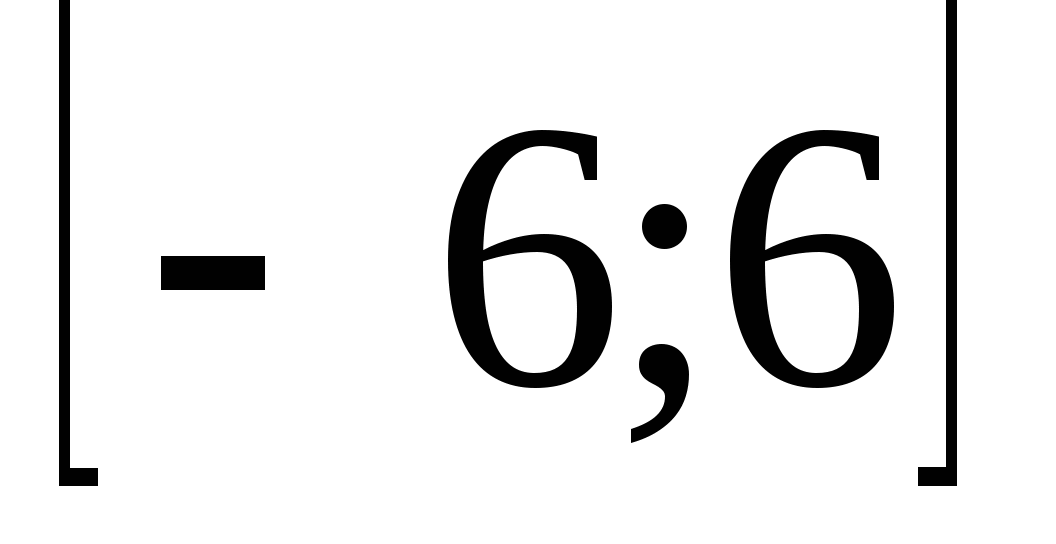
3. Ее область значений

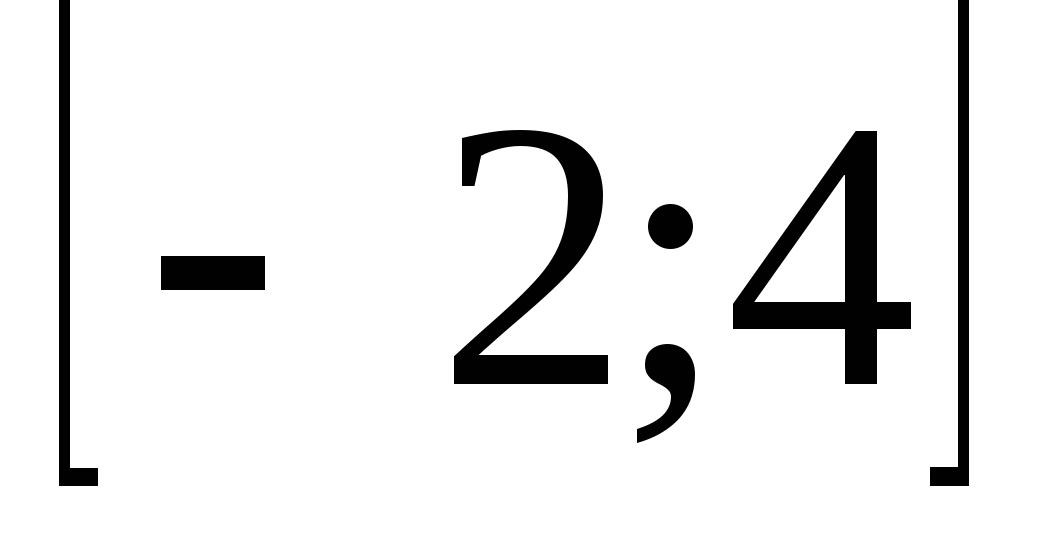
4. У нее 2 точки минимума и 1 точка максимума

5. На промежутке 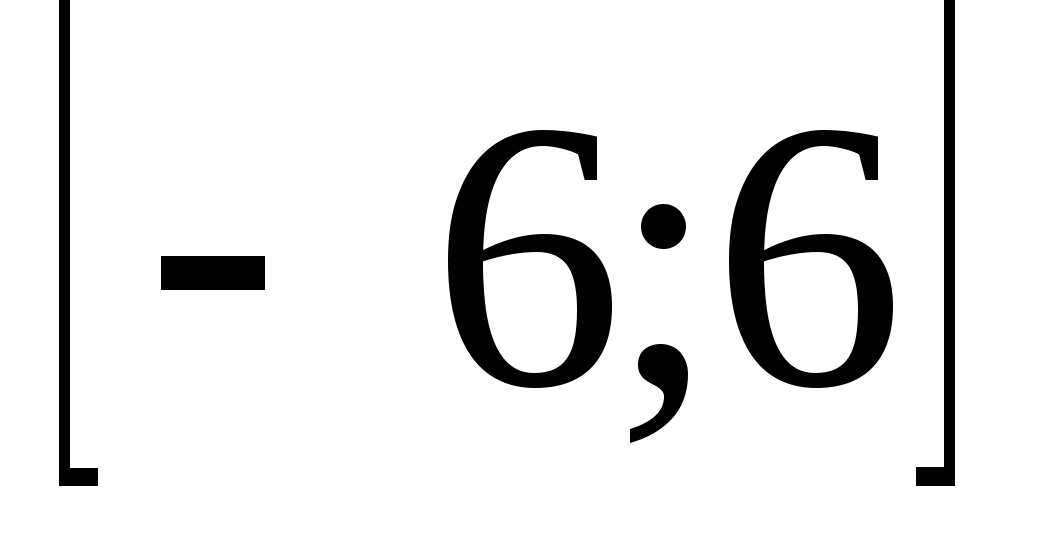она имеет 4 нуля, среди которых 1 и 5.

6. 

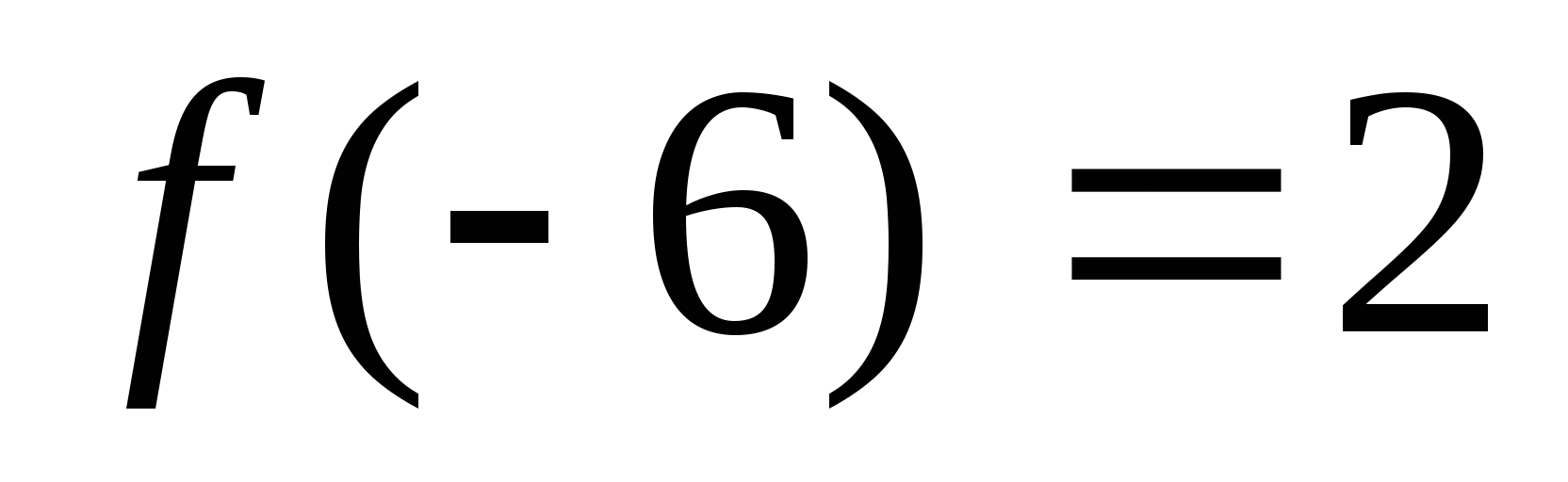
7. Один из промежутков возрастания

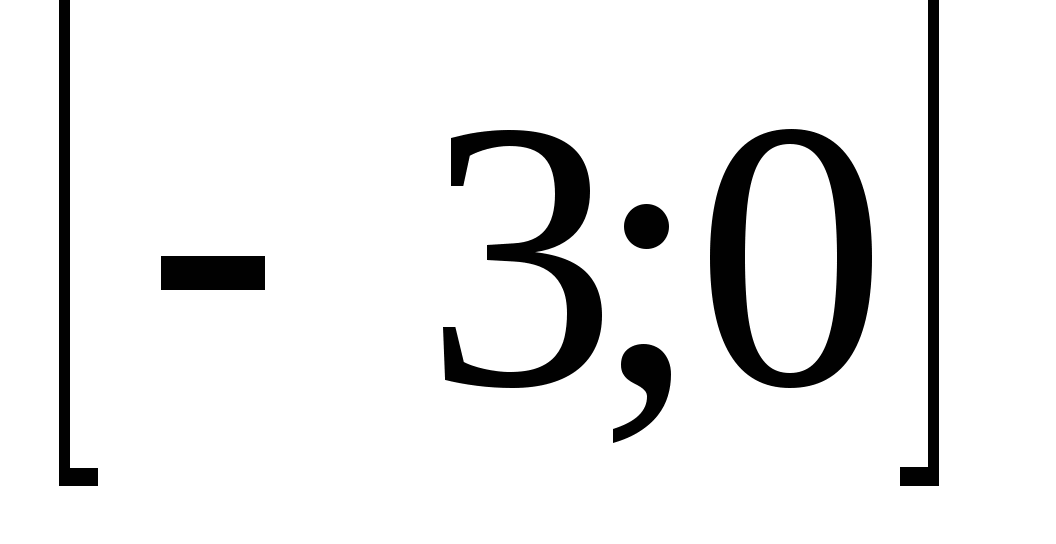
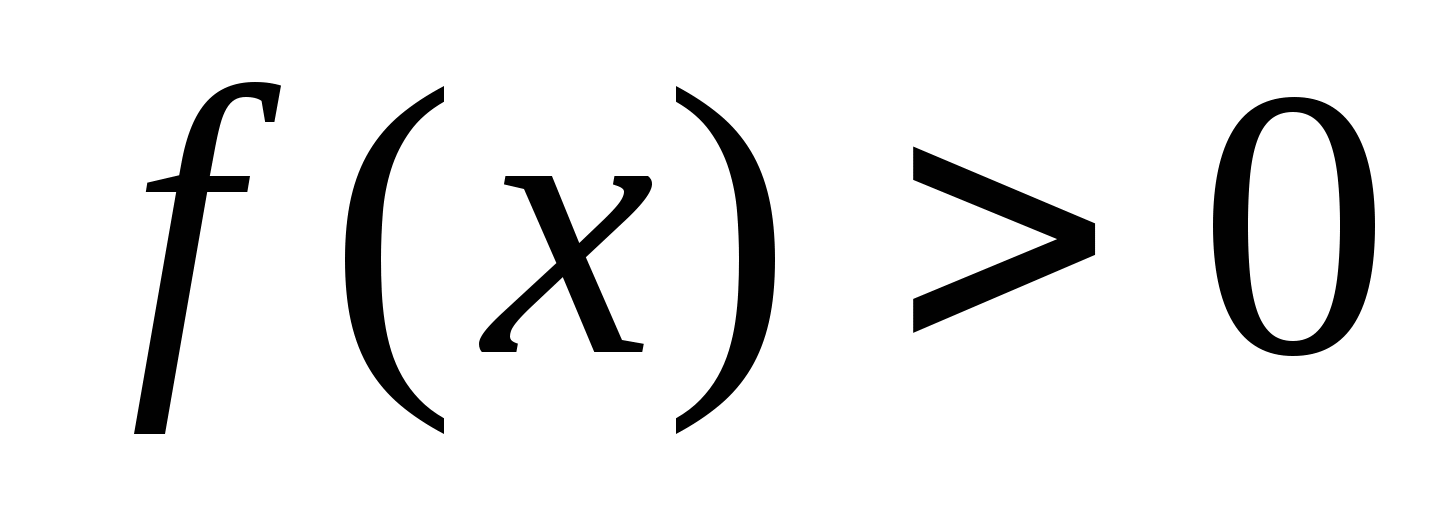8. на промежутках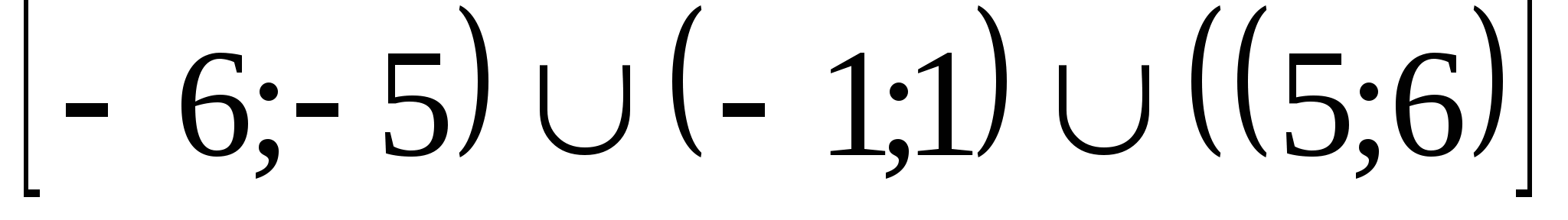

1. Область определения функции Вариант 1 Приложение 2 (тест)

2. Максимум функции

3.Сколько точек экстремума имеет функция на отрезке ?

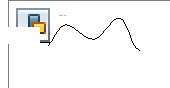
4.На каком рисунке 1 - 4 функция убывает на отрезке ?

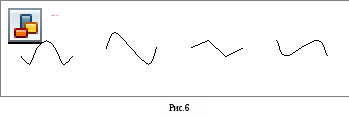
5. Укажите график четной функции

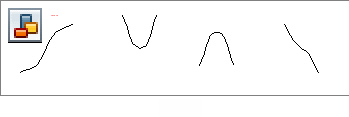
6. Укажите график функции, принимающей положительные значения на промежутке

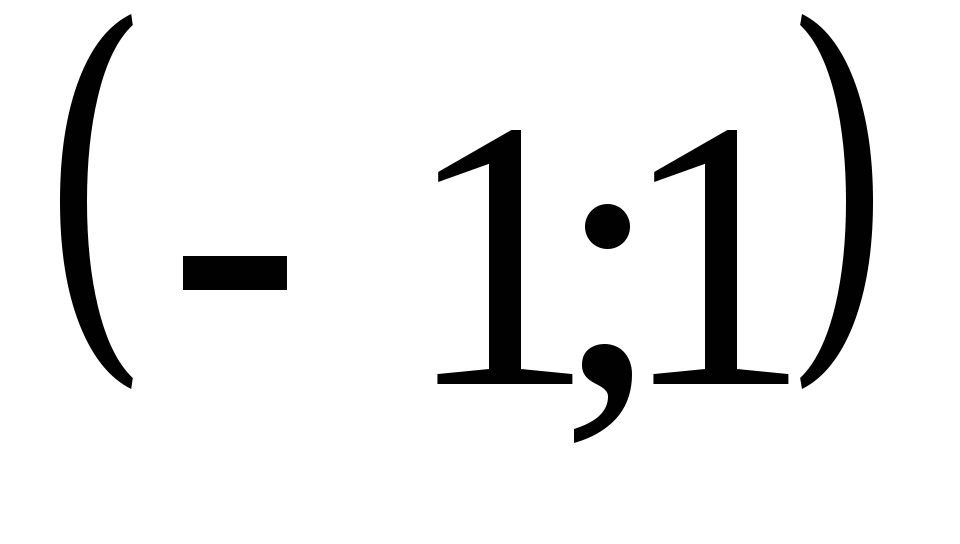
1. Множество значений функции, Вариант 2

2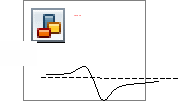. Минимум функции на отрезке ,

3. Сколько точек максимума имеет функция на отрезке ?

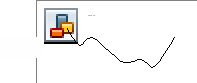
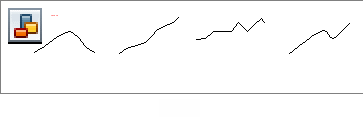
4. На каком из рисунков 1 - 4 функция возрастает на отрезке ?

5. Укажите график нечетной функции

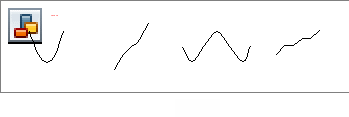
6.Укажите график функции, принимающая отрицательные значения на промежутке .