- Учителю
- Рабочая программа по математике 6 класс автор учебника Н. Я. Виленкин
Рабочая программа по математике 6 класс автор учебника Н. Я. Виленкин


































 Раздел I. Пояснительная записка.
Раздел I. Пояснительная записка.
Настоящая программа по математике для 6 класса образовательной школы создана на основе нормативных документов:
-
Стандарт среднего (полного) образования по математике. Базовый уровень. Базисный учебный план 2004г.
-
Обязательный минимум основного общего образования по математике.
-
Требования к уровню подготовки выпускников по математике.
-
Нормы оценки знаний, умений и навыков учащихся по математике.
-
При создании рабочей программы по математике 6 класс использована Программа. Планирование учебного материала. Математика. 5-6 классы/авт.-сост. В.И. Жохов. - М.:Мнемозина,2010.
Программа детализирует и раскрывает содержание стандарта, определяет общую стратегию обучения, воспитания и развития учащихся средствами учебного предмета в соответствии с целями изучения математики, которые определены стандартом.
Изучение математики в 6 классе направлено на достижение следующих целей:
-
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
-
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе, свойственных математической деятельности: ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;
-
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
-
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, играющей особую роль в общественном развитии.
В ходе преподавания математики в 6 классе, работы над формированием у учащихся перечисленных в программе знаний и умений, следует обратить внимание на то, чтобы они овладевали умениями общеучебного характера, разнообразными способами деятельности, приобретали опыт:
-
работы с математическими моделями, приемами их построения и исследования;
-
методами исследования реального мира, умения действовать в нестандартных ситуациях;
-
решения разнообразных классов задач из различных разделов курса, в том числе задач, требующих поиска пути и способов решения;
-
исследовательской деятельности, развития идей, проведения экспериментов, обобщения, постановки и формулирования новых задач;
-
ясного, точного, грамотного изложения своих мыслей в устной и письменной речи;
-
использования различных языков математики (словесного, символического, графического), свободного перехода с одного языка на другой для иллюстрации, интерпретации, аргументации;
-
проведения доказательных рассуждений, аргументации, выдвижения гипотез и их обоснования;
-
поиска, систематизации, анализа и классификации информации, использования разнообразных информационных источников, включая учебную и справочную литературу, современные информационные технологии.
Тематическое планирование конкретизирует содержание предметных тем образовательного стандарта и дает примерное поурочное распределение учебных часов.
Согласно федеральному базисному учебному плану на изучение математики в 6 классах отводится 170 часов из расчета 5ч в неделю.
В рабочей программе предусмотрено 15 контрольных работ:
-
Делимость чисел
-
Сложение, вычитание дробей с разными знаменателями
-
Сложение, вычитание дробей с разными знаменателями
-
Умножение и деление обыкновенных дробей
-
Умножение и деление обыкновенных дробей
-
Умножение и деление обыкновенных дробей
-
Отношения и пропорции
-
Отношения и пропорции
-
Положительные и отрицательные числа
-
Сложение и вычитание положительных и отрицательных чисел
-
Умножение и деление положительных и отрицательных чисел
-
Решение уравнений
-
Решение уравнений
-
Координаты на плоскости
-
Итоговая контрольная работа
Требования к математической подготовке.
В результате изучения курса математики учащиеся должны:
-
Правильно употреблять термины, связанные с различными видами чисел и способами их записи: цельное, дробное, десятичная дробь, переход от одной формы записи к другой (например, проценты в виде десятичной дроби; выделение целой части из неправильной дроби); решать три основные задачи на дроби;
-
Сравнивать числа, упорядочивать наборы чисел, понимать связь отношений «больше», «меньше» с расположением точек на координатной прямой; находить среднее арифметическое нескольких чисел;
-
Выполнять арифметические действия с натуральными числами и десятичными дробями; округлять десятичные дроби;
-
Распознавать на чертежах и моделях геометрические фигуры (отрезки, углы, треугольники, многоугольники, окружность, круг); изображать указанные геометрические фигуры; владеть практическими навыками использования геометрических инструментов для построения и измерения отрезков и углов;
-
Владеть навыками вычисления по формулам, знать основные единицы измерения и уметь перейти от одних единиц измерения к другим в соответствии с условиями задачи;
-
Находить числовые значения буквенных выражений.
Основные развивающие и воспитательные цели
Развитие:
-
Ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;
-
Математической речи;
-
Сенсорной сферы; двигательной моторики;
-
Внимания; памяти;
-
Навыков само и взаимопроверки.
Формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов.
Воспитание:
-
Культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса;
-
Волевых качеств;
-
Коммуникабельности;
-
Ответственности.
НОРМЫ ОЦЕНКИ ЗНАНИЙ, УМЕНИЙ И НАВЫКОВ
УЧАЩИХСЯ ПО МАТЕМАТИКЕ
ОЦЕНКА УСТНОГО ОТВЕТА
Отметка «5»
-
ответ полный и правильный на основании изученного материала;
-
материал изложен в определенной логической последовательности, литературным языком;
-
ответ самостоятельный.
Отметка «4»
-
ответ полный и правильный на основании изученного материала;
-
материал изложен в определенной логической последовательности, при этом допущены две-три несущественные ошибки, исправленные по требованию учителя.
Отметка «3»
-
ответ полный, но при этом допущена существенная ошибка или ответ неполный, несвязный.
Отметка «2»
- при ответе обнаружено непонимание учащимся основного содержания учебного материала или допущены существенные ошибки, которые учащийся не может исправить при наводящих вопросах учителя.
Отметка «2» отмечает такие недостатки в подготовке ученика, которые являются серьезным препятствием к успешному овладению последующим материалом.
Отметка «1»
-
отсутствие ответа;
-
полное незнание или непонимание материала.
Отметка («5», «4», «3») может ставиться не только за единовременный ответ (когда на проверку подготовки ученика отводится определенное время), но и за рассредоточенный во времени, т.е. сумму ответов, данных учеником на протяжении урока (выводится поурочный балл), при условии, если в процессе урока не только заслушивались ответы учащегося, но и осуществлялась проверка его умения применять полученные знания.
Нормы оценки знаний умений и навыков учащихся при проверке
письменных контрольных, самостоятельных и практических работ
Оценка "5"
Оценка "5" ставится:
а) работа выполнена полностью и без ошибок;
б) количество недочетов в такой работе не должно превышать двух.
Оценка "4"
Оценка "4" ставится:
а) работа выполнена полностью, но содержит не более 3-4 недочетов;
б) из всех предложенных заданий не выполнено одно задание;
в) содержит одну грубую ошибку.
Оценка "3"
Оценка "3" ставится:
а) выполнено верно половина из всех предложенных заданий
б) работа содержит не более 5-7 недочетов.
Оценка "2"
Оценка "2" ставится во всех остальных случая
Грубые ошибки.
К грубым ошибкам относятся ошибки, которые обнаруживают незнание учащимися формул, правил, основных свойств, теорем и неумение их применять, незнание приемов решения задач, рассматриваемых в учебных пособиях, а также вычислительные ошибки, если он не являются опиской.
Негрубые ошибки.
К негрубым ошибкам относятся:
- потеря корня или сохранение в ответе постороннего корня;
- отбрасывание без объяснения одного из корня и равнозначные им.
К недочетам относятся:
- нерациональное решение, описки, недостаточность;
- отсутствие пояснений, обоснований в решениях.
Если одна и та же ошибка (один и тот же недочет) встречаются несколько раз, то это рассматривается как одна ошибка (один недочет).
Зачеркивание в работе (желательно, чтобы они были аккуратными) свидетельствует о поисках решения, что считать ошибкой не следует.
Раздел II. Учебно-тематический план.
Тематическое планирование к учебнику «Математика,6»,
авт. Н. Я. Виленкина, В.И. Жохова и др.
6 класс (5 ч в неделю, всего 170 ч)
1. Делимость чисел (20 ч)
Делители и кратные числа. Общий делитель и общее кратное. Признаки делимости на 2, 3, 5, 9, 10. Простые и составные числа. Разложение натурального числа на простые множители.
Основная цель - завершить изучение натуральных чисел, подготовить основу для освоения действий с обыкновенными дробями.
В данной теме завершается изучение вопросов, связанных с натуральными числами. Основное внимание должно быть уделено знакомству с понятиями «делитель» и «кратное», которые находят применение при сокращении обыкновенных дробей и при их приведении к общему знаменателю. Упражнения полезно выполнять с опорой на таблицу умножения - прямым подбором.
Определенное внимание уделяется знакомству с признаками делимости, понятиям простого и составного чисел. При их изучении целесообразно формировать умения проводить простейшие умозаключения, обосновывая свои действия ссылками на определение, правило.
Учащиеся должны уметь разложить число на множители. Например, они должны понимать, что 36 = 6· 6 = 4· 9 = 2 ·18 и т. п. Умения разложить число на простые множители не обязательно добиваться от всех учащихся.
2. Сложение и вычитание дробей с разными знаменателями (22 ч)
Основное свойство дроби. Сокращение дробей. Приведение дробей к общему знаменателю. Понятие о наименьшем общем знаменателе нескольких дробей. Сравнение дробей. Сложение и вычитание дробей. Решение текстовых задач.
Основная цель - выработать прочные навыки преобразования дробей, сложения и вычитания дробей.
Одним из важнейших результатов обучения является усвоение основного свойства дроби, применяемого для преобразования дробей: сокращения, приведения к новому знаменателю. Умение приводить дроби к общему знаменателю используется для сравнения дробей.
При рассмотрении действий с дробями используются правила сложения и вычитания дробей с одинаковыми знаменателями, понятие смешанного числа. Важно обратить внимание на случай вычитания дроби из целого числа.
3. Умножение и деление обыкновенных дробей (32 ч)
Умножение и деление обыкновенных дробей. Основные задачи на дроби.
Основная цель - выработать прочные навыки арифметических действий с обыкновенными дробями и решения основных задач на дроби.
В этой теме завершается работа над формированием навыков арифметических действий с обыкновенными дробями. Навыки должны быть достаточно прочными, чтобы учащиеся не испытывали затруднений в вычислениях с рациональными числами, чтобы алгоритмы действий с обыкновенными дробями могли стать в дальнейшем опорой для формирования умений выполнять действия с алгебраическими дробями.
Расширение аппарата действий с дробями позволяет решать текстовые задачи, в которых требуется найти дробь от числа или число по данному значению его дроби.
4. Отношения и пропорции (19 ч)
Пропорция. Основное свойство пропорции. Решение задач с помощью пропорции. Понятия о прямой и обратной пропорциональности величин. Задачи на пропорции. Масштаб. Формулы длины окружности и площади круга. Шар.
Основная цель - сформировать понятия пропорции, прямой и обратной пропорциональности величин.
Необходимо, чтобы учащиеся усвоили основное свойство пропорции, так как оно находит применение на уроках математики, химии, физики. В частности, достаточное внимание должно быть уделено решению с помощью пропорции задач на проценты.
Понятия о прямой и обратной пропорциональности величин можно сформировать как обобщение нескольких конкретных примеров, подчеркнув при этом практическую значимость этих понятий, возможность их применения для упрощения решения соответствующих задач.
В данной теме даются представления о длине окружности и площади круга. Соответствующие формулы к обязательному материалу не относятся. Рассмотрение геометрических фигур завершается знакомством с шаром.
5. Положительные и отрицательные числа (13 ч)
Положительные и отрицательные числа. Противоположные числа. Модуль числа и его геометрический смысл. Сравнение чисел. Целые числа. Изображение чисел на координатной прямой. Координата точки.
Основная цель - расширить представления учащихся о числе путем введения отрицательных чисел.
Целесообразность введения отрицательных чисел показывается на содержательных примерах. Учащиеся должны научиться изображать положительные и отрицательные числа на координатной прямой. В дальнейшем она будет служить наглядной основой для правил сравнения чисел, сложения и вычитания чисел.
Специальное внимание должно быть уделено усвоению вводимого здесь понятия модуля числа, прочное знание которого необходимо для формирования умения сравнивать отрицательные числа, а в дальнейшем и для овладения алгоритмами арифметических действий с положительными и отрицательными числами.
6. Сложение и вычитание положительных и отрицательных чисел (11 ч)
Сложение и вычитание положительных и отрицательных чисел.
Основная цель - выработать прочные навыки сложения и вычитания положительных и отрицательных чисел.
Действия с отрицательными числами вводятся на основе представлений об изменении величин: сложение и вычитание чисел иллюстрируется соответствующими перемещениями точек координатной прямой. При изучении данной темы отрабатываются алгоритмы сложения и вычитания при выполнении действий с целыми и дробными числами.
7. Умножение и деление положительных и отрицательных чисел (12 ч)
Умножение и деление положительных и отрицательных чисел. Понятие о рациональном числе. десятичное приближение обыкновенной дроби. Применение законов арифметических действий для рационализации вычислений.
Основная цель - выработать прочные навыки арифметических действий с положительными и отрицательными числами.
Навыки умножения и деления положительных и отрицательных чисел отрабатываются сначала при выполнении отдельных действий, а затем в сочетании с навыками сложения и вычитания при вычислении значений числовых выражений.
При изучении данной темы учащиеся должны усвоить, что для обращения обыкновенной дроби в десятичную достаточно разделить (если это возможно) числитель на знаменатель. В каждом конкретном случае они должны знать, в какую дробь обращается данная обыкновенная дробь - в десятичную или периодическую. Учащиеся должны знать представление в виде десятичной дроби таких дробей, как
![]()
8. Решение уравнений (15 ч)
Простейшие преобразования выражений: раскрытие скобок, приведение подобных слагаемых. Решение линейных уравнений. Примеры решения текстовых задач с помощью линейных уравнений.
Основная цель - подготовить учащихся к выполнению преобразований выражений, решению уравнений.
Преобразования буквенных выражений путем раскрытия скобок и приведения подобных слагаемых отрабатываются в той степени, в которой они необходимы для решения несложных уравнений.
Введение арифметических действий над отрицательными числами позволяет ознакомить учащихся с общими приемами решения линейных уравнений с одной переменной.
9. Координаты на плоскости (13 ч)
Построение перпендикуляра к прямой и параллельных прямых с помощью чертежного треугольника и линейки. Прямоугольная система координат на плоскости, абсцисса и ордината точки. Примеры графиков, диаграмм.
Основная цель - познакомить учащихся с прямоугольной системой координат на плоскости.
Учащиеся должны научиться распознавать и изображать перпендикулярные и параллельные прямые. Основное внимание следует уделить отработке навыков их построения с помощью линейки и чертежного треугольника, не требуя воспроизведения точных определений.
Основным результатом знакомства учащихся с координатной плоскостью должны стать знания порядка записи координат точек плоскости и их названий, умения построить координатные оси, отметить точку по заданным координатам, определить координаты точки, отмеченной на координатной плоскости.
Формированию вычислительных и графических умений способствует построение столбчатых диаграмм. При выполнении соответствующих упражнений найдут применение изученные ранее сведения о масштабе и округлении чисел.
10. Повторение. Решение задач (13 ч)
Раздел III. Содержание тем учебного курса.
1. ДЕЛИМОСТЬ ЧИСЕЛ (20ч)
Делители и кратные.
Признаки делимости на 10, 5 и 2.
Признаки делимости на 3 и на 9.
Простые и составные числа.
Разложение на простые множители.
Наибольший общий делитель. Взаимно простые числа.
Наименьшее общее кратное.
Знать и понимать:
-
Делители и кратные числа.
-
Признаки делимости на 2,3,5,10.
-
Простые и составные числа.
-
Разложение числа на простые множители.
-
Наибольший общий делитель.
-
Наименьшее общее кратное.
Уметь:
-
Находить делители и кратные числа.
-
Находить наибольший общий делитель двух или трех чисел.
-
Находить наименьшее общее кратное двух или трех чисел.
Раскладывать число на простые множители
2. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ С РАЗНЫМИ ЗНАМЕНАТЕЛЯМИ (22ч)
Основное свойство дроби.
Сокращение дробей.
Приведение дробей к общему знаменателю.
Сравнение дробей с разными знаменателями.
Сложение, вычитание дробей с разными знаменателями.
Сложение и вычитание смешанных чисел.
Знать и понимать:
-
Обыкновенные дроби.
-
Сократимая дробь.
-
Несократимая дробь.
-
Основное свойство дроби.
-
Сокращение дробей.
-
Сравнение дробей.
-
Сложение и вычитание дробей с разными знаменателями.
Уметь:
-
Сокращать дроби.
-
Приводить дроби к общему знаменателю.
-
Складывать и вычитать обыкновенные дроби с разными знаменателями.
Сравнивать дроби, упорядочивать наборы дробей.
3. УМНОЖЕНИЕ И ДЕЛЕНИЕ ОБЫКНОВЕННЫХ ДРОБЕЙ (32ч)
Умножение дробей.
Нахождение дроби от числа.
Применение распределительного свойства умножения.
Взаимно обратные числа.
Деление.
Нахождение числа по его дроби.
Дробные выражения.
Знать и понимать:
-
Умножение дробей.
-
Нахождение части числа.
-
Распределительное свойство умножения
-
Взаимно обратные числа.
-
Нахождение числа по его части.
Уметь:
-
Умножать обыкновенные дроби.
-
Находить часть числа.
-
Находить число обратное данному.
-
Выполнять деление обыкновенных дробей.
-
Находить число по его дроби.
-
Находить значения дробных выражений
4. ОТНОШЕНИЯ И ПРОПОРЦИИ (19ч)
Отношения
Пропорции.
Прямая и обратная пропорциональные зависимости.
Знать и понимать:
-
Отношения.
-
Пропорции.
-
Основное свойство пропорции.
-
Пропорциональные и обратно пропорциональные величины.
Уметь:
-
Составлять и решать пропорции.
Решать задачи с помощью пропорций на прямую и обратную пропорциональные зависимости
Масштаб.
Длина окружности, площадь круга.
Шар.
Знать и понимать:
-
Формула длины окружности.
-
Формула площади круга.
-
Масштаб. Шар.
Уметь:
-
Решать задачи по формулам.
Решать задачи с использованием масштаба.
5. ПОЛОЖИТЕЛЬНЫЕ И ОТРИЦАТЕЛЬНЫЕ ЧИСЛА (13ч)
Координаты на прямой.
Противоположные числа.
Модуль числа.
Сравнение чисел.
Изменение величин.
Знать и понимать:
-
Противоположные числа.
-
Координаты на прямой.
-
Модуль числа.
Уметь:
-
Находить для числа противоположное ему число.
-
Находить модуль числа.
Сравнивать рациональные числа.
6. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ПОЛОЖИТЕЛЬНЫХ И ОТРИЦАТЕЛЬНЫХ ЧИСЕЛ (11ч)
Сложение чисел с помощью координатной прямой.
Сложение отрицательных чисел.
Сложение чисел с разными знаками.
Вычитание.
Знать и понимать:
-
Правило сложения отрицательных чисел.
-
Правило сложения двух чисел с разными знаками.
-
Вычитание рациональных чисел
-
Сложение чисел с помощью координатной прямой.
Уметь:
-
Складывать числа с помощью координатной плоскости.
-
Складывать и вычитать рациональные числа.
7. УМНОЖЕНИЕ И ДЕЛЕНИЕ ПОЛОЖИТЕЛЬНЫХ И ОТРИЦАТЕЛЬНЫХ ЧИСЕЛ (12ч)
Умножение.
Деление.
Рациональные числа.
Знать и понимать:
-
Понятие рациональных чисел.
Уметь:
-
Выполнять умножение и деление рациональных чисел
-
Свойства действий с рациональными числами
-
Применять свойства действий с рациональными числами для преобразования выражений
8. РЕШЕНИЕ УРАВНЕНИЙ (15ч)
Раскрытие скобок.
Коэффициент.
Подобные слагаемые.
Решение уравнений.
Знать и понимать:
-
Подобные слагаемые.
-
Коэффициент выражения.
-
Правила раскрытия скобок.
Уметь:
-
Раскрывать скобки.
-
Приводить подобные слагаемые
-
Применять свойства уравнения для нахождения его решения.
9. КООРДИНАТЫ НА ПЛОСКОСТИ (13ч)
Параллельные прямые.
Координатная плоскость.
Столбчатые диаграммы.
Графики.
Знать и понимать:
-
Перпендикулярные прямые.
-
Параллельные прямые.
-
Координатная плоскость.
-
Координаты точки.
-
Столбчатая диаграмма.
-
График зависимости.
Уметь:
-
Изображать координатную плоскость.
-
Строить точку по заданным координатам.
-
Находить координаты изображенной в координатной плоскости точки.
-
Строить столбчатые диаграммы.
-
Находить значения величин по графикам зависимостей.
10 ПОВТОРЕНИЕ (13ч)
Действия с обыкновенными дробями.
Действия с обыкновенными дробями.
Сложение и вычитание чисел с разными знаками.
Умножение и деление чисел с разными знаками.
Решение уравнений.
Координаты на плоскости. Графики.
Календарно-тематическое планирование уроков
№
урока
Название темы
К-во
часов
Даты
Формируемые знания, умения
Форма контроля
Использование учебно-технического оборудования
§1. ДЕЛИМОСТЬ ЧИСЕЛ
20 уроков
1.09-28.09
Знать и понимать:
-
Делители и кратные числа.
-
Признаки делимости на 2,3,5,10.
-
Простые и составные числа.
-
Разложение числа на простые множители.
-
Наибольший общий делитель.
-
Наименьшее общее кратное.
Уметь:
-
Находить делители и кратные числа.
-
Находить наибольший общий делитель двух или трех чисел.
-
Находить наименьшее общее кратное двух или трех чисел.
Раскладывать число на простые множители
1
Делители и кратные (п.1)
1
2
Делители и кратные
1
3
Делители и кратные
1
С.Р.
мультимедиа проектор
4
Признаки делимости на 10, 5 и 2 (п. 2)
1
5
Признаки делимости на 10, 5 и 2
1
6
Признаки делимости на 10, 5 и 2
1
С.Р.
7
Признаки делимости на 3 и на 9 (п. 3)
1
8
Признаки делимости на 3 и на 9
1
9
Простые и составные числа (п. 4)
1
10
Простые и составные числа
1
С.Р.
11
Разложение на простые множители (п. 5)
1
мультимедиа
проектор
12
Разложение на простые множители
1
13
Наибольший общий делитель. Взаимно простые числа (п. 6)
1
С.Р.
14
Наибольший общий делитель. Взаимно простые числа
1
мультимедиа
проектор
15
Наибольший общий делитель. Взаимно простые числа
1
16
Наименьшее общее кратное (п. 7)
1
С.Р.
17
Наименьшее общее кратное
1
мультимедиа
проектор
18
Наименьшее общее кратное
1
19
Наименьшее общее кратное
1
20
Контрольная работа №1 по теме «Делимость чисел»
1
26.09-28.09
К.Р.
§2.
СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ С РАЗНЫМИ ЗНАМЕНАТЕЛЯМИ
22
урока
29.09-30.09
21
Основное свойство дроби (п. 8)
1
Знать и понимать:
-
Обыкновенные дроби.
-
Сократимая дробь.
-
Несократимая дробь.
-
Основное свойство дроби.
-
Сокращение дробей.
-
Сравнение дробей.
-
Сложение и вычитание дробей с разными знаменателями.
Уметь:
-
Сокращать дроби.
-
Приводить дроби к общему знаменателю.
-
Складывать и вычитать обыкновенные дроби с разными знаменателями.
Сравнивать дроби, упорядочивать наборы дробей.
Мультимедиа
проектор
22
Основное свойство дроби
1
С.Р.
23
Сокращение дробей (п. 9)
1
24
Сокращение дробей
1
25
Сокращение дробей
1
С.Р.
26
Приведение дробей к общему знаменателю (п. 10)
1
мультимедиа
проектор
27
Приведение дробей к общему знаменателю
1
28
Приведение дробей к общему знаменателю
1
С.Р.
29
Сравнение, сложение, вычитание дробей с разными знаменателями (п. 11)
1
мультимедиа
проектор
30
Сравнение, сложение, вычитание дробей с разными знаменателями
1
31
Сравнение, сложение, вычитание дробей с разными знаменателями
1
С.Р.
32
Сравнение, сложение, вычитание дробей с разными знаменателями
1
33
Сравнение, сложение, вычитание дробей с разными знаменателями
1
34
Сравнение, сложение, вычитание дробей с разными знаменателями
1
35
Контрольная работа №2 по теме «Сравнение, сложение, вычитание дробей с разными знаменателями»
1
18.10-20.10
К.Р.
36
Сложение и вычитание смешанных чисел (п. 12)
1
мультимедиа
проектор
37
Сложение и вычитание смешанных чисел
1
38
Сложение и вычитание смешанных чисел
1
С.Р.
39
Сложение и вычитание смешанных чисел
1
40
Сложение и вычитание смешанных чисел
1
41
Сложение и вычитание смешанных чисел
1
42
Контрольная работа №3 по теме «Сложение и вычитание дробей с разными знаменателями»
28.10-30.10
К.Р.
§ 3. УМНОЖЕНИЕ И ДЕЛЕНИЕ ОБЫКНОВЕННЫХ ДРОБЕЙ
32
урока
31.10-04.11
43
Умножение дробей (п. 13)
1
Знать и понимать:
-
Умножение дробей.
-
Нахождение части числа.
-
Распределительное свойство умножения
-
Взаимно обратные числа.
-
Нахождение числа по его части.
Уметь:
-
Умножать обыкновенные дроби.
-
Находить часть числа.
-
Находить число обратное данному.
-
Выполнять деление обыкновенных дробей.
-
Находить число по его дроби.
-
Находить значения дробных выражений
мультимедиа
проектор
44
Умножение дробей
1
45
Умножение дробей
1
46
Умножение дробей
1
С.Р.
47
Итоговый урок по материалу I четверти
1
48
Нахождение дроби от числа (п.14)
1
мультимедиа
проектор
49
Нахождение дроби от числа
1
50
Нахождение дроби от числа
1
51
Нахождение дроби от числа
1
С.Р.
52
Применение распределительного свойства умножения (п. 15)
1
мультимедиа
проектор
53
Применение распределительного свойства умножения
1
54
Применение распределительного свойства умножения
1
С.Р.
55
Применение распределительного свойства умножения
1
56
Применение распределительного свойства умножения
1
57
Контрольная работа №4 по теме «Умножение обыкновенных дробей»
1
22.1-24.11
К.Р.
58
Взаимно обратные числа (п. 16)
1
мультимедиа
проектор
59
Взаимно обратные числа
1
С.Р.
60
Деление (п. 17)
1
мультимедиа
проектор
61
Деление
1
62
Деление
1
С.Р.
63
Деление
1
64
Деление
1
65
Контрольная работа №5 по теме «Деление обыкновенных дробей»
1
04.12-06.12
К.Р.
66
Нахождение числа по его дроби (п. 18)
1
мультимедиа
проектор
67
Нахождение числа по его дроби
1
68
Нахождение числа по его дроби
1
С.Р.
69
Нахождение числа по его дроби
1
70
Нахождение числа по его дроби
1
71
Дробные выражения (п. 19)
1
С.Р.
мультимедиа
проектор
72
Дробные выражения
1
73
Дробные выражения
1
74
Контрольная работа №6 по теме «Деление и умножение обыкновенных дробей»
1
17.12-19.12
К.Р.
§4.ОТНОШЕНИЯ И ПРОПОРЦИ
19
уроков
20.12-27.01
75
Отношения (п. 20)
1
Знать и понимать:
-
Отношения.
-
Пропорции.
-
Основное свойство пропорции.
-
Пропорциональные и обратно пропорциональные величины.
Уметь:
-
Составлять и решать пропорции.
Решать задачи с помощью пропорций на прямую и обратную пропорциональные зависимости
Масштаб.
Длина окружности, площадь круга.
Шар.
Знать и понимать:
-
Формула длины окружности.
-
Формула площади круга.
-
Масштаб. Шар.
Уметь:
-
Решать задачи по формулам.
Решать задачи с использованием масштаба.
мультимедиа
проектор
76
Отношения
1
77
Отношения
1
С.Р.
78
Отношения
1
79
Отношения
1
80
Пропорции (п. 21)
1
мультимедиа
проектор
81
Пропорции
1
С.Р.
82
Повторение. Решение задач. Обобщение материала II четверти
1
83
Прямая и обратная пропорциональные зависимости (п. 22)
1
мультимедиа
проектор
84
Прямая и обратная пропорциональные зависимости
1
С.Р.
85
Прямая и обратная пропорциональные зависимости
1
86
Контрольная работа №7 по теме «Отношения и пропорции»
1
15.01-17.01
К.Р.
87
Масштаб (п. 23)
1
мультимедиа
проектор
88
Масштаб
1
89
Длина окружности, площадь круга (п. 24)
1
90
Длина окружности, площадь круга
1
С.Р.
91
Шар (п. 25)
1
мультимедиа
проектор
92
Шар
1
93
Контрольная работа №8 по теме «Отношения и пропорции»
1
25.01-27.01
К.Р.
§ 5. ПОЛОЖИТЕЛЬНЫЕ И ОТРИЦАТЕЛЬНЫЕ ЧИСЛА
13
уроков
28.01-15.02
94
Координаты на прямой (п. 26)
1
Знать и понимать:
-
Противоположные числа.
-
Координаты на прямой.
-
Модуль числа.
Уметь:
-
Находить для числа противоположное ему число.
-
Находить модуль числа.
Сравнивать рациональные числа.
мультимедиа
проектор
95
Координаты на прямой
1
96
Координаты на прямой
1
С.Р.
97
Противоположные числа (п. 27)
1
мультимедиа
проектор
98
Противоположные числа
1
99
Модуль числа (п. 28)
1
100
Модуль числа
1
С.Р.
101
Сравнение чисел (п. 29)
1
мультимедиа
проектор
102
Сравнение чисел
1
103
Сравнение чисел
1
С.Р.
104
Изменение величин (п. 30)
1
105
Изменение величин
1
106
Контрольная работа № 9 по теме «Положительные и отрицательные числа»
1
13.02-15.02
К.Р.
§ 6.Сложение и вычитание положительных и отрицательных чисел
11
уроков
16.02-01.03
107
Сложение чисел с помощью координатной прямой (п. 31)
1
Знать и понимать:
-
Правило сложения отрицательных чисел.
-
Правило сложения двух чисел с разными знаками.
-
Вычитание рациональных чисел
-
Сложение чисел с помощью координатной прямой.
Уметь:
-
Складывать числа с помощью координатной плоскости.
-
Складывать и вычитать рациональные числа.
мультимедиа
проектор
108
Сложение чисел с помощью координатной прямой
1
109
Сложение отрицательных чисел (п. 32)
1
110
Сложение отрицательных чисел
1
С.Р.
111
Сложение чисел с разными знаками (п. 33)
1
мультимедиа
проектор
112
Сложение чисел с разными знаками
1
113
Сложение чисел с разными знаками
1
114
Вычитание (п. 34)
1
С.Р.
115
Вычитание
1
116
Вычитание
1
117
Контрольная работа №10 по теме «Сложение и вычитание положительных и отрицательных чисел»
1
27.02-01.03
К.Р.
§7. УМНОЖЕНИЕ И ДЕЛЕНИЕ ПОЛОЖИТЕЛЬНЫХ И ОТРИЦАТЕЛЬНЫХ ЧИСЕЛ
12
уроков
02.03-18.03
118
Умножение (п. 35)
1
Знать и понимать:
-
Понятие рациональных чисел.
Уметь:
-
Выполнять умножение и деление рациональных чисел
-
Свойства действий с рациональными числами
-
Применять свойства действий с рациональными числами для преобразования выражений
мультимедиа
проектор
119
Умножение
1
120
Умножение
1
С.Р.
121
Деление (п. 36)
1
мультимедиа
проектор
122
Деление
1
123
Деление
1
С.Р.
124
Рациональные числа (п. 37)
1
125
Рациональные числа
1
126
Контрольная работа №11 по теме « Умножение и деление рациональных чисел. Свойства действий с рациональными числами»
1
12.03-14-03
К.Р.
127
Свойства действий с рациональными числами (п. 38)
1
мультимедиа
проектор
128
Свойства действий с рациональными числами
1
129
Свойства действий с рациональными числами
1
С.Р.
§8. РЕШЕНИЕ УРАВНЕНИЙ
15
уроков
19.03-15.04
130
Раскрытие скобок (п. 39)
1
Знать и понимать:
-
Подобные слагаемые.
-
Коэффициент выражения.
-
Правила раскрытия скобок.
Уметь:
-
Раскрывать скобки.
-
Приводить подобные слагаемые
-
Применять свойства уравнения для нахождения его решения.
мультимедиа
проектор
131
Раскрытие скобок
1
132
Уроки повторения и обобщения по материалу III четверти
1
С.Р.
133
Уроки повторения и обобщения по материалу III четверти
1
134
Коэффициент (п. 40)
1
мультимедиа
проектор
135
Коэффициент
1
С.Р.
136
Подобные слагаемые (п.41)
1
мультимедиа
проектор
137
Подобные слагаемые
1
138
Подобные слагаемые
1
139
Контрольная работа №12 по теме «Решение уравнений»
1
07.04-09.04
К.Р.
140
Решение уравнений (п.42)
1
мультимедиа
проектор
141
Решение уравнений
1
142
Решение уравнений
1
143
Решение уравнений
1
144
Контрольная работа №13 по теме «Решение уравнений»
1
13.04-15.04
К.Р.
§9 КООРДИНАТЫ НА ПЛОСКОСТИ
13
уроков
16.04-06.05
145
Перпендикулярные прямые (п.43)
1
Знать и понимать:
-
Перпендикулярные прямые.
-
Параллельные прямые.
-
Координатная плоскость.
-
Координаты точки.
-
Столбчатая диаграмма.
-
График зависимости.
Уметь:
-
Изображать координатную плоскость.
-
Строить точку по заданным координатам.
-
Находить координаты изображенной в координатной плоскости точки.
-
Строить столбчатые диаграммы.
-
Находить значения величин по графикам зависимостей.
мультимедиа
проектор
146
Перпендикулярные прямые
1
147
Параллельные прямые (п.44)
1
мультимедиа
проектор
148
Параллельные прямые
1
С.Р.
149
Координатная плоскость (п.45)
1
мультимедиа
проектор
150
Координатная плоскость
1
151
Координатная плоскость
1
С.Р.
152
Столбчатые диаграммы (п.46)
1
мультимедиа
проектор
153
Столбчатые диаграммы
1
154
Графики (п.47)
1
С.Р.
мультимедиа
проектор
155
Графики
1
156
Графики
1
157
Контрольная работа №14 по теме «Координаты на плоскости»
1
04.05-06.05
К.Р.
ИТОГОВОЕ ПОВТОРЕНИЕ КУРСА
МАТЕМАТИКИ 5-6-ГО КЛАССОВ
13
уроков
158
Действия с дробями
1
159
Действия с дробями
1
160
Сложение и вычитание чисел с разными знаками
1
161
Сложение и вычитание чисел с разными знаками
1
С.Р.
162
Умножение и деление чисел с разными знаками
1
163
Умножение и деление чисел с разными знаками
1
164
Решение уравнений
1
С.Р.
165
Решение уравнений
1
166
Координаты на плоскости
1
167
Итоговая контрольная работа №15
1
К.Р.
168
Повторение. Решение задач.
1
169
Повторение. Решение задач.
1
170
Повторение. Решение задач.
1
Раздел IV. Контрольно-измерительные материалы.
Содержание:
-
Тест № 1 Делимость чисел. Признаки делимости.
-
Тест № 2 Сложение и вычитание дробей.
-
Тест № 3 Умножение и деление дробей.
-
Тест № 4 Отношения и пропорции
-
Тест № 5 Положительные и отрицательные числа.
-
Тест № 6 Сложение положительных и отрицательных чисел
-
Тест № 7 Умножение и деление положительных и отрицательных чисел
-
Тест № 8 Решение уравнений
-
Тест № 9 Координаты на плоскости
-
Тест № 10 ИТОГОВЫЙ ТЕСТ
ТЕСТ №1
Тема: Делимость чисел. Признаки делимости.
Вариант 1
-
Какие из данных утверждений не верны:
1) 3 делитель 26; 2) 37 делитель 814;
3) 23 делитель 943; 4) 67 делитель 3350;
5) 4 делитель 4; 6) 0 делитель 5.
а) 1 и 6; б) 1, 4 и 6; в) 1, 5 и 6; г) свой ответ.
-
Какие из данных утверждений верны?
-
33 кратно 11; 2) 565 кратно 15;
-
3) 67 кратно 67; 4) 672 кратно 1;
5) 17 кратно 0; 6) 45 кратно 2.
а) 1, 3, 4; б) 1, 2, 3; в) 1, 2, 3, 4; г) свой ответ.
-
Какое из данных выражений принимает только нечетные значения, если a и b - нечетные натуральные числа и a>b?
а) a+b; б) a-b; в) a·b; г) 2a-2b.
-
Какие из данных сумм кратны 5:
1) 7316+97564; 2) 4523+7415;
3) 678+991+31; 4) 230+179.
а) 1 и 3; б) 1 и 4; в) 1; г) таких нет.
-
Какие из данных чисел не кратны 3:
1) 1706; 2) 12364; 3) 40215;
4) 131421; 5) 18279.
а) 1 и 5; б) 1 и 2; в) 1 и 4; г) свой ответ.
-
Найдите остаток от деления числа 78567 на 5.
а) 1; б) 2; в) 3; г) свой ответ.
-
Разложите на простые множители число 420.
а) 420 = 2·2·3·5·7; б) 420 = 1·2·2·3·5·7; в) 420 = 4·3·5·7;
г) свой ответ.
-
У каких из предложенных пар чисел НОД равен 4:
1) 24 и 20; 2) 24 и 30; 3) 24 и 32;
4) 18 и 32; 5) 4 и 16.
а) 2, 3, 5; б) 1, 5; в) 1, 3, 5; г) у всех.
-
У каких из предложенных пар чисел НОК равно 24:
1) 24 и 2; 2) 18 и 12; 3) 3 и 8;
4) 12 и 32; 5) 4 и 6.
а) 1 и 3; б) 1 и 5; в) 1; г) свой ответ.
-
Сколько существует двузначных чисел кратных 11, но не кратных 33?
а) 6; б) 5; в) 4; г) свой ответ.
ТЕСТ №1
Тема: Делимость чисел. Признаки делимости.
Вариант 2
-
Какие из данных утверждений верны:
-
7 делитель 85; 2) 73 делитель 876;
-
3) 16 делитель 849; 4) 23 делитель 1288;
5) 1 делитель 4; 6) 0 делитель 5.
а) 1, 2, 5; б) 1, 4 и 5; в) 1, 5; г) свой ответ.
-
Какие из данных утверждений не верны?
-
56 кратно 14; 2) 765 кратно 15;
-
3) 11 кратно 11; 4) 78 кратно 1;
5) 7 кратно 0; 6) 85 кратно 9.
а) 1, 3, 4; б) 1, 2, 3; в) 1, 2, 3, 4; г) свой ответ.
-
Какое из данных выражений принимает только четные значения, если a и b - нечетные натуральные числа и a>b?
а) a·b; б) b+2; в) a+2b; г) a-b.
-
Какие из данных сумм не кратны 5:
1) 7314+454; 2) 45232+74158;
3) 378+981+31; 4) 260+149.
а) 1 и 5; б) 1 и 2; в) 1 и 4; г) таких нет.
-
Какие из данных чисел кратны 3:
1) 3366; 2) 37564; 3) 23415;
4) 678991; 5) 23179.
а) 1 и 5; б) 1 и 3; в) 1 и 4; г) таких нет
-
Найдите остаток от деления числа 87656 на 9.
а) 3; б) 5; в) 1; г) свой ответ.
-
Разложите на простые множители число 280.
а) 280 = 2·2·2·5·7; б) 280 = 1·2·2·2·5·7; в) 280 = 8·5·7;
г) свой ответ.
-
У каких из предложенных пар чисел НОД равен 6:
1) 24 и 20; 2) 24 и 30; 3) 24 и 32;
4) 18 и 30; 5) 6 и 200.
а) 2, 4; б) 1, 3; в) 1, 2, 4, 5; г) у всех.
-
У каких из предложенных пар чисел НОК равно 60:
1) 30 и 2; 2) 18 и 15; 3) 4 и 15;
4) 12 и 60; 5) 10 и 6.
а) 2, 3, 4; б) 3 и 4; в) 2, 4; г) у всех
-
Сколько существует двузначных чисел кратных 12, но не кратных 24?
а) 5; б) 3; в) 4; г) свой ответ.
ТЕСТ №1
Тема: Делимость чисел. Признаки делимости.
Вариант 3
-
Какие из данных утверждений не верны:
-
17 делитель 635; 2) 4 делитель 43;
-
3) 26 делитель 494; 4) 98 делитель 1078;
5) 5 делитель 5; 6) 0 делитель 31.
а) 1, 4, 5; б) 5 и 6; в) 1, 3, 5; г) свой ответ.
2. Какие из данных утверждений верны?
-
55 кратно 5; 2) 167 кратно 12;
3) 236 кратно 6; 4) 41 кратно 41;
5) 324 кратно 1; 6) 13 кратно 0.
а) 1, 4, 5, 6; б) 1, 5, 3; в) 1, 5, 4; г) свой ответ.
3. Какое из данных выражений принимает только нечетные значения, если a - четное и b - нечетное натуральные числа и a>2b?
а) a+b; б) 3a-2b; в) a·b; г) 2a-2b.
4. Какие из данных сумм кратны 10:
1) 221+346+123; 2) 3654+2136;
3) 7231+231; 4) 451+458.
а) 3, 4; б) 1 и 3; в) 1 и 2; г) таких нет.
-
Какие из данных чисел не кратны 9:
1) 3453; 2) 4347; 3) 123030;
4) 697211; 5) 3591954.
а) 1 и 2; б) 4 и 2; в) 1, 3 и 4; г) свой ответ.
-
Найдите остаток от деления числа 94587 на 6.
а) 2; б) 9; в) 3; г) свой ответ.
-
Разложите на простые множители число 884.
а) 884 = 4·13·17; б) 884 = 1·2·2·13·17; в) 884 = 2·2·221;
г) свой ответ.
-
У каких из предложенных пар чисел НОД равен 6:
1) 48 и 72; 2) 24 и 30; 3) 42 и 54;
4) 24 и 16; 5) 6 и 8.
а) 1, 2, 3; б) 2, 3, 4; в) 2, 3; г) у всех.
-
У каких из предложенных пар чисел НОК равно 36:
1) 6 и 6; 2) 6 и 36; 3) 12 и 3;
4) 9 и 4; 5) 18 и 2.
а) 1, 2 и 3; б) 2 и 4; в) 2, 4, 5; г) свой ответ.
-
Сколько существует двузначных чисел кратных 7, но не кратных 21?
а) 10; б) 11; в) 9; г) свой ответ.
ТЕСТ №1
Тема: Делимость чисел. Признаки делимости.
Вариант 4
1. Какие из данных утверждений верны:
-
1 делитель 35; 2) 8 делитель 999;
3) 4 делитель 4; 4) 0 делитель 1799;
5) 9 делитель 81; 6) 17 делитель 985.
а) 2, 3, 4; б) 3, 5; в) 1, 5 и 3; г) свой ответ.
-
Какие из данных утверждений не верны?
-
31 кратно 2; 2) 565 кратно 5;
-
3) 121 кратно 1; 4) 17 кратно 0;
5) 8 кратно 2; 6) 74 кратно 8.
а) 4; б) 1, 4, 6; в) 3, 4; г) свой ответ.
-
Какое из данных выражений принимает только нечетные значения, если a и b - четные натуральные числа и a>b?
а) 3a·b; б) 2a+b+1; в) a+3b; г) 3a-b.
-
Какие из данных сумм не кратны 10:
1) 1526+344; 2) 78901+43281;
3) 527+343+81; 4) 380+120.
а) 1 и 5; б) 2 и 3; в) 1 и 4; г) таких нет.
-
Какие из данных чисел кратны 9:
1) 89946; 2) 25215; 3) 46827;
4) 789002; 5) 5607.
а) 1, 3 и 5; б) 1 и 5; в) 3 и 4; г) таких нет.
-
Найдите остаток от деления числа 43278 на 7.
а) 8; б) 4; в) 3; г) свой ответ.
-
Разложите на простые множители число 490.
а) 490 = 2·5·49; б) 490 = 1·2·5·7·7; в) 490 = 2·2·5·7;
г) свой ответ.
-
У каких из предложенных пар чисел НОД равен 8:
1) 24 и 40; 2) 48 и 64; 3) 8 и 234;
4) 24 и 16; 5) 24 и 32.
а) 1, 4, 5; б) 1, 2; в) 1, 4; г) свой ответ
-
У каких из предложенных пар чисел НОК равно 72:
1) 8 и 9; 2) 36 и 2; 3) 21 и 3;
4) 18 и 4; 5) 72 и 2.
а) 1, 3, 5; б) 2, 3, 4; в) 1, 5; г) у всех.
-
Сколько существует двузначных чисел кратных 9, но не кратных 36?
а) 9; б) 10; в) 11; г) свой ответ.
ТЕСТ №2
Тема: Сложение и вычитание дробей
Вариант 1
-
Какие числа следует подставить вместо букв a, b, c и d, чтобы все равенства оказались верными:
1)  2)
2)  ; 3)
; 3)  ; 4)
; 4) 
а) a=48, b= 8, c=3, d= 12; б) a=48, b= 6, c=5, d= 12
в) a=48, b= 12, c=6, d= 20 г) свой ответ
-
Сократите дробь

а)  б)
б)  ; в)
; в)  ; г) свой ответ
; г) свой ответ
-
Найдите наименьший общий знаменатель дробей
 ,
,  и
и  :
:
а) 66; б) 132; в) 33; г) свой ответ.
-
Какие из дробей можно представить в виде десятичных:
1)  ; 2) ; 3) ; 4)
; 2) ; 3) ; 4)  ; 5)
; 5)  ; 6)
; 6) 
а) 1 и 5; б) 1, 5, 6; в) 1, 4, 6; г) свой ответ.
-
Вася пробежал дистанцию 90 м за 14 с, Коля 100 м за 15 с, а Петя - 110 м за 16 с. У кого из мальчиков средняя скорость больше?
а) у Васи; б) у Пети; в) у Коли; г) у всех одинакова.
-
В каком из примеров в ответе получится число 0,45?
а)  ; б)
; б)  ; в)
; в)  ; г)
; г) 
-
Решите уравнение x +

а)  ; б)
; б)  ; в) 1,1; г) свой ответ.
; в) 1,1; г) свой ответ.
-
Найдите значение выражения: (0,6 -
 ) - (
) - ( - 0,4)
- 0,4)
а) 0,5; б)  ; в) вычислить нельзя; г) свой ответ.
; в) вычислить нельзя; г) свой ответ.
-
При каком натуральном a значение выражения
 равно 2?
равно 2?
а) 7; б) 14; в) ни при каком; г) свой ответ.
-
Сколько существует натуральных b, при которых
 ?
?
а) 10; б) 12; в) таких нет; г) свой ответ.
ТЕСТ №2
Тема: Сложение и вычитание дробей
Вариант 2
-
Какие числа следует подставить вместо букв a, b, c и d, чтобы все равенства оказались верными:
1)  2)
2) 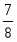 ; 3)
; 3) 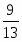 ; 4)
; 4) 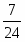
а) a=9, b= 82, c=4, d= 20; б) a=9, b= 72, c=5, d= 20;
в) a=9, b= 12, c=5, d= 24; г) свой ответ
-
Сократите дробь
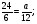
а) 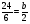 б)
б) 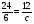 ; в)
; в) 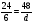 ; г) свой ответ
; г) свой ответ
-
Найдите наименьший общий знаменатель дробей
 ,
, 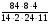 и
и 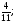 :
:
а) 35; б) 140; в) 70; г) свой ответ.
-
Какие из дробей можно представить в виде десятичных:
1)  ; 2)
; 2)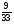 ; 3)
; 3)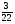 ; 4)
; 4)  ; 5)
; 5) 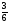 ; 6)
; 6) 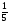
а) 1 и 5; б) 1, 5, 6; в) 1, 4, 6; г) свой ответ.
-
Маша разложила 34 кг ягод в 11 одинаковых пакетов, Лена - 38 кг ягод в 12 пакетов, а Галя - 40 кг в 16 пакетов. У кого из девочек более вместительные пакеты?
а) у Маши; б) у Лены; в) у Гали; г) у всех одинаковые
-
В каком из примеров в ответе получится число 0,35?
а) 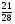 ; б)
; б) 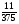 ; в)
; в) 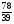 ; г)
; г) 
-
Решите уравнение x -
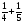
а) 1,1; б) 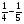 ; в)
; в) 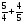 ; г) свой ответ.
; г) свой ответ.
-
Найдите значение выражения: (1,6 -
 ) - (0,4+
) - (0,4+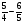 )
)
а) 0,7; б) 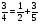 ; в) вычислить нельзя; г) свой ответ.
; в) вычислить нельзя; г) свой ответ.
-
При каком натуральном a значение выражения
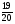 равно 1?
равно 1?
а) 12; б) 24; в) свой ответ; г) ни при каком.
-
Сколько существует натуральных b, при которых
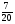 ?
?
а) 8; б) 6; в) таких нет; г) свой ответ.
ТЕСТ №2
Тема: Сложение и вычитание дробей
Вариант 3
-
Какие числа следует подставить вместо букв a, b, c и d, чтобы все равенства оказались верными:
1) 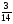 2)
2) 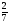 ; 3)
; 3) 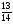 ; 4)
; 4) 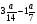
а) a=36, b= 6, c=4, d= 16; б) a=36, b= 8, c=4, d= 16;
в) a=36, b= 12, c=4, d= 24; г) свой ответ
-
Сократите дробь
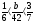
а) 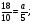 б)
б) 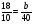 ; в)
; в) 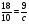 ; г) свой ответ
; г) свой ответ
-
Найдите наименьший общий знаменатель дробей
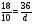 ,
, 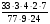 и
и 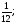 :
:
а) 102; б) 34; в) 16; г) свой ответ.
-
Какие из дробей можно представить в виде десятичных:
1) 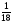 ; 2)
; 2)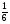 ; 3)
; 3)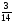 ; 4)
; 4) 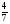 ; 5)
; 5) 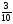 ; 6)
; 6) 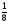
а) 2, 4 и 5; б) 2 и 4; в) 2 и 5; г) свой ответ.
-
Первая черепаха проползла 6 м за 7 часов, вторая - 7 м за 8 часов, а третья - 8 м за 9 часов. У какой из черепах была большая средняя скорость?
а) у первой; б) у второй; в) у третьей;
г) у всех одинакова
-
В каком из примеров в ответе получится число 0,05?
а)  ; б)
; б)  ; в)
; в)  ; г)
; г) 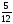
-
Решите уравнение x +
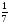
а) 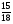 ; б)
; б) 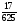 ; в)
; в) 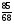 ; г) свой ответ.
; г) свой ответ.
-
Найдите значение выражения: (1,75 -
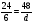 ) - (0,25+
) - (0,25+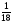 )
)
а) 1; б) 2; в) вычислить нельзя; г) свой ответ.
-
При каком натуральном a значение выражения
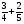 равно 2?
равно 2?
а) 24; б) 12; в) ни при каком; г) свой ответ
-
Сколько существует натуральных b, при которых
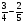 ?
?
а) 14; б) 12; в) таких нет; г) свой ответ.
ТЕСТ №2
Тема: Сложение и вычитание дробей
Вариант 4
-
Какие числа следует подставить вместо букв a, b, c и d, чтобы все равенства оказались верными:
1) 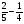 2)
2) 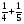 ; 3)
; 3) 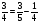 ; 4)
; 4) 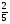
а) a=1, b= 16, c=16, d= 12; б) a=1, b= 4, c=96, d= 24;
в) a=1, b= 32, c=48, d= 6; г) свой ответ
-
Сократите дробь
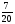
а) 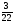 б)
б)  ; в)
; в) 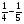 ; г) свой ответ
; г) свой ответ
-
Найдите наименьший общий знаменатель дробей
 ,
, 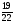 и
и 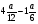 :
:
а) 180; б) 90; в) 270; г) свой ответ.
-
Какие из дробей можно представить в виде десятичных:
1) 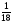 ; 2)
; 2)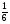 ; 3)
; 3)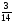 ; 4)
; 4) 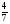 ; 5)
; 5) 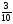 ; 6)
; 6) 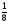
а) 1, 3 и 5; б) 3, 5, 6; в) 3 и 5; г) свой ответ.
-
Турист шел три дня. В первый день он прошел 33 км за 6 часов, во второй - 38,5 км за 7 часов, а в третий - 27,5 км за 5 часов. В какой из дней у него была наибольшая средняя скорость?
а) в первый; б) во второй; в) в третий; г) одинаковая
-
В каком из примеров в ответе получится число 0,15?
а) 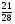 ; б)
; б) 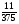 ; в)
; в) 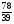 ; г)
; г) 
-
Решите уравнение x +
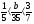
а) 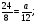 ; б) 3,1; в)
; б) 3,1; в) 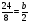 ; г) свой ответ.
; г) свой ответ.
-
Найдите значение выражения: (2,4 -
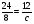 ) - (1,6+
) - (1,6+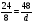 )
)
а) 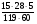 ; б) 3,5; в) вычислить нельзя; г) свой ответ.
; б) 3,5; в) вычислить нельзя; г) свой ответ.
-
При каком натуральном a значение выражения
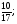 равно 6?
равно 6?
а) 7; б) 18; в) свой ответ; г) ни при каком
-
Сколько существует натуральных b, при которых
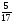 ?
?
а) 9; б) 7; в) таких нет; г) свой ответ.
ТЕСТ №3
Тема: Умножение и деление дробей.
Вариант 1
-
В бочонке
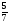 кг меда. Сколько меда в 6 бочонках?
кг меда. Сколько меда в 6 бочонках?
а) 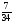 кг; б)
кг; б) 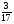 кг; в)
кг; в) 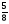 кг; г) свой ответ
кг; г) свой ответ
-
В каком из примеров в ответе получится число 0,3:
а) 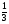 ; б)
; б) 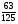 ; в)
; в) 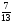 ; г)
; г) 
-
Турист проходит в среднем
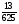 км в час. Какое расстояние он пройдет за
км в час. Какое расстояние он пройдет за 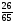 часа?
часа?
а) 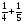 км; б) 5 км; в)
км; б) 5 км; в) 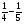 км; г) свой ответ
км; г) свой ответ
-
Ящик, вмещающий 34 кг яблок, заполнен на
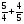 своего объема. Сколько еще яблок можно положить в ящик?
своего объема. Сколько еще яблок можно положить в ящик?
а) 13,6 кг; б) 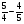 кг; в) 20,4 кг; г) свой ответ
кг; в) 20,4 кг; г) свой ответ
-
Какое из чисел больше остальных:
а) 20% от 18,3; б) 50% от 5,95; в) 17% от 17,9; г) 23% от 14
-
У какого из выражений значение равно 12?
а) 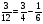 ; б)
; б) 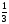 ;
;
в) 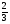 ; г) такого нет
; г) такого нет
-
Решите уравнение (
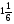
а) 6; б) 5,8; в) 8; г) свой ответ
-
Укажите все пары взаимно обратных чисел:
1)  и 5; 2) и
и 5; 2) и 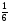 ; 3)
; 3) 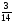 и
и 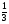 ;
;
4) 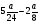 и
и 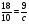 ; 5) 6,5 и
; 5) 6,5 и 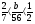 ; 6) 1,25 и 0,8
; 6) 1,25 и 0,8
а) 3; б) 1, 2; в) 2, 4, 6; г) свой ответ
-
В каком из примеров в ответе получится 2,2:
а) 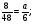 :
: 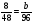 +0,2; б) 2,7 -
+0,2; б) 2,7 - 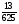 :
: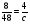 ;
;
в) 11:6+14:3-3,1; г) 1,75· 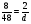 :
: 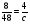
-
Найдите значение выражения
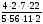
а) 0,6; б) 0,06; в) 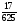 ; г) свой ответ
; г) свой ответ
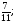
ТЕСТ №3
Тема: Умножение и деление дробей.
Вариант 2
-
В банке
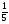 л компота. Сколько компота в 4 банках?
л компота. Сколько компота в 4 банках?
а) 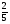 л; б)
л; б) 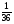 л; в)
л; в) 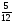 л; г) свой ответ
л; г) свой ответ
-
В каком из примеров в ответе получится число 0,3:
а) 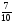 ; б)
; б) 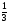 ; в)
; в) 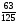 ; г)
; г) 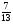
-
Корова съедает за месяц
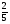 стога сена. Сколько стогов сена она съест за
стога сена. Сколько стогов сена она съест за  месяца?
месяца?
а) 4; б) 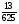 ; в)
; в) 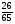 ; г) свой ответ
; г) свой ответ
-
Молочная цистерна емкостью 625 л заполнена на
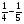 своего объема. Сколько еще молока можно налить в эту цистерну?
своего объема. Сколько еще молока можно налить в эту цистерну?
а) 375 л; б) 250 л; в) 345 л; г) свой ответ
-
Какое из чисел больше остальных:
а) 10% от 82,6; б) 40% от 59,5;
в) 25% от 23,14; г) 16% от 47,4
-
У какого из выражений значение равно 28?
а) 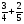 ; б)
; б) 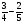 :
:  ;
;
в) 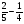 ; г) такого нет
; г) такого нет
-
Решите уравнение (
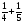 : 25= 0,04
: 25= 0,04
а) 16,375; б) 0,625; в) 3; г) свой ответ
-
Укажите все пары взаимно обратных чисел:
1) 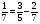 и 5; 2)
и 5; 2) 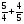 и
и 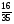 ; 3)
; 3) 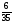 и
и 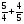 ;
;
4) 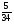 и
и 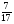 ; 5) 1,2 и
; 5) 1,2 и 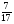 ; 6) 1,5 и 0,66
; 6) 1,5 и 0,66
а) 1, 2; б) 3; в) 2, 4, 1; г) свой ответ
-
В каком из примеров в ответе получится 7,5:
а) 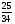
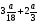 ; б)
; б) 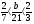 ;
;
в) 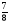 :
: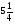 ; г) 1,8·
; г) 1,8· 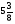 :
: 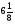
-
Найдите значение выражения
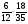
а)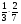 ; б) 1,5; в) 0,08; г) свой ответ
; б) 1,5; в) 0,08; г) свой ответ
ТЕСТ №3
Тема: Умножение и деление дробей.
Вариант 3
-
В коробке
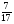 кг конфет. Сколько конфет в 8 коробках?
кг конфет. Сколько конфет в 8 коробках?
а) 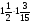 кг; б)
кг; б) 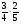 кг; в)
кг; в) 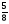 кг; г) свой ответ
кг; г) свой ответ
-
В каком из примеров в ответе получится число 0,36:
а) 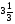 ; б)
; б) 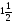 ; в)
; в) 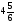 ; г)
; г) 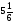
-
Лодка проплывает в среднем
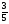 км в час. Какое расстояние она проплывет за
км в час. Какое расстояние она проплывет за 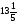 часа?
часа?
а) 8,1 км; б) 11,2 км; в) 121 км; г) свой ответ
-
Поле площадью 168 га засеяно на
 . Сколько еще осталось засеять?
. Сколько еще осталось засеять?
а) 48 га; б) 120 га; в) 140 га; г) свой ответ
-
Какое из чисел больше остальных:
а) 20% от 14; б) 50% от 2,3;
в) 17% от 5,96; г) 23% от 17,9
-
У какого из выражений значение равно 48?
а) 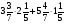 ; б)
; б) 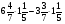 ·
·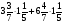 ;
;
в) 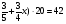 ; г) такого нет
; г) такого нет
-
Решите уравнение (
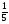 ·44= 16
·44= 16
а) 3,25; б) 0,75; в) 1,75; г) свой ответ
-
Укажите все пары взаимно обратных чисел:
1) 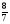 и 6; 2)
и 6; 2) 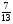 и
и 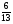 ; 3)
; 3) 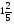 и
и 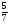 ;
;
4) 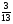 и
и 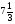 ; 5) 1,625 и
; 5) 1,625 и 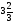 ; 6) 2,5 и 0,4
; 6) 2,5 и 0,4
а) 2; б) 2, 3, 4; в) 3, 4, 5; г) свой ответ
-
В каком из примеров в ответе получится 8,2:
а) 9,8 - 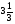 ; б)
; б) 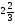 ;
;
в) 5,6:2,8 + 6,3·0,5; г) 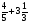
-
Найдите значение выражения
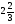
а)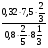 ; б) 1,05; в)
; б) 1,05; в) 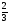 ; г) свой ответ
; г) свой ответ
ТЕСТ №3
Тема: Умножение и деление дробей.
Вариант 4
-
В автомобиль вмещается
 т груза. Сколько груза перевезут за раз 8 таких же автомобилей?
т груза. Сколько груза перевезут за раз 8 таких же автомобилей?
а) 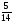 т; б)
т; б) 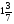 т; в)
т; в) 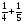 т; г) свой ответ
т; г) свой ответ
-
В каком из примеров в ответе получится число 1,2:
а) 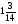 ; б)
; б) 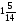 ; в)
; в) 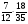 ; г)
; г) 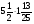
-
Насос перекачивает
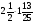 м3 воды в час. Сколько воды он перекачает за
м3 воды в час. Сколько воды он перекачает за 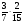 часа?
часа?
а) 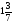 ; б)
; б) 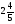 ; в) 4 м3; г) свой ответ
; в) 4 м3; г) свой ответ
-
Аквариум емкостью 154 л наполнен водой на
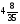 . Сколько еще воды можно долить в аквариум?
. Сколько еще воды можно долить в аквариум?
а) 112 л; б) 44 л; в) 124 л; г) свой ответ
-
Какое из чисел больше остальных:
а) 20% от 55,2; б) 12% от 36,84;
в) 35% от 42,4; г) 70% от 18,55
-
У какого из выражений значение равно 16?
а) 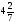 ; б)
; б) 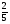 ·
·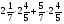 ;
;
в) 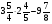 ; г) такого нет
; г) такого нет
-
Решите уравнение (
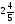 · 100 = 295
· 100 = 295
а) 9; б) 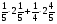 ; в)
; в) 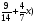 ; г) свой ответ
; г) свой ответ
-
Укажите все пары взаимно обратных чисел:
1) 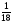 и 9; 2) 1,6 и
и 9; 2) 1,6 и 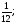 ; 3)
; 3) 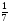 и 9;
и 9;
4) 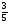 и
и 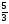 ; 5) 0,7 и
; 5) 0,7 и 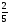 ; 6) 3 и 0,33
; 6) 3 и 0,33
а) 3; б) 3, 6; в) 3, 2, 5; г) свой ответ
-
В каком из примеров в ответе получится 3,4:
а) 10,8 + 3,7:1,5; б) 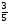 :
: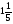 ;
;
в) 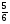 :
: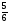 ; г)
; г) 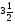 :
: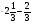
-
Найдите значение выражения
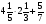
а) 5,6; б) 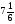 ; в)
; в) 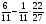 ; г) свой ответ
; г) свой ответ
ТЕСТ №4
Тема: Отношения и пропорции
Вариант 1
-
Какое из данных отношений равно
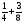 :
:
а) 7:2; б) 4:12; в) 7:17,5; г) свой ответ
-
Найдите отношение 1,2 м к 10 см:
а) 12; б) 12 м; в) 12 см; г) свой ответ
-
Из данных пропорций выберите верные:
1) 22:22=81:81; 2) 82:72=64:78;
3) 6,7:3,35=45,8:22,9; 4) 8,73:12=6,12:14,4;
5) 17:2=34:4; 6) 15:8=13:6
а) 1, 3, 5; б) 1, 5; в) 1, 3, 4; г) свой ответ
-
Найдите неизвестный член пропорции: 4:х=5,6:0,07
а) 0,05; б) 20; в) 0,5; г) свой ответ
-
За 3 ч Вася прополол 60% участка. За какое время он сможет дополоть участок, если будет работать с той же производительностью?
а) за 1 ч; б) за 3 ч; в) за 2 ч; г) свой ответ
-
Из молока получается 14% творога. Сколько молока требуется для получения 5,6 кг творога?
а) 18 кг; б) 25 кг; в) 780 кг; г) свой ответ
-
Длина дороги на местности составляет 3,2 км, а на карте 4 см. Определите масштаб карты.
а) 1:80000; б) 1:8000; в) 1:800000; г) свой ответ
-
Найдите площадь окружности, диаметр которой равен
8 см.
а) 50,24 см2; б) 412,56см2;
в) 55,8 см2; г) свой ответ
-
Тележное колесо, радиус которого 30 см, сделало 300 оборотов. Какое расстояние проехала телега? Ответ выразите в метрах.
а) 282,6 м; б) 565,2 м; в) 558 м; г) свой ответ
-
Сумма двух чисел составляет 180% первого слагаемого. На сколько процентов первое слагаемое больше второго?
а) на 25%; б) на 20%;
в) на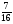 %; г) свой ответ
%; г) свой ответ
ТЕСТ №4
Тема: Отношения и пропорции
Вариант 2
-
Какое из данных отношений равно
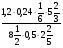 :
:
а) 6:11; б) 27,5:15; в) 26,5:15; г) свой ответ
-
Найдите отношение 150 г к 1,5 кг:
а) 0,01; б) 0,1; в) 0,1 г; г) свой ответ
-
Из данных пропорций выберите верные:
1) 11:26=26:11; 2) 14:70=10:50;
3) 0,56:0,05=25,8:2,96; 4) 121:1,1=583:5,3;
5) 45:12=18:8; 6) 0:15=0:34
а) 1, 3, 5; б) 1, 5; в) 1, 3, 4; г) свой ответ
-
Найдите неизвестный член пропорции: х:0,9=1,6:3
а) 4,8; б) 0,48; в)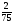 ; г) свой ответ
; г) свой ответ
-
За 6 ч фермер собрал 40% имеющихся вишен. За какое время он сможет собрать остальную вишню, если будет работать с той же производительностью?
а) за 15 ч; б) за 9 ч; в) за 11 ч; г) свой ответ
-
Из сахарной свеклы получается 12% сахара. Сколько свеклы требуется для получения 8,4 т сахара?
а) 61,6 т; б) 70 т; в) 80 т; г) свой ответ
-
Длина железнодорожного полотна на местности составляет 1,2 км, а на карте 6 см. Определите масштаб карты.
а) 1:2000; б) 1:200; в) 1:500; г) свой ответ
-
Найдите площадь окружности, диаметр которой равен
4 дм.
а) 12,56 дм2; б) 50,24 дм2;
в) 3,14 дм2; г) свой ответ
-
Найдите диаметр окружности, если ее длина 37,68 м. Ответ выразите в дециметрах.
а) 6 дм; б) 60 дм; в) 12 дм; г) свой ответ
-
Разность двух чисел составляет 80% уменьшаемого. На сколько процентов уменьшаемое больше вычитаемого?
а) на 80%; б) на 40%;
в) на 400%; г) свой ответ
ТЕСТ №4
Тема: Отношения и пропорции
Вариант 3
-
Какое из данных отношений равно
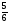 :
:
а) 5:4; б) 6,4:8; в) 24,45:92,5; г) свой ответ
-
Найдите отношение 1,5 мин к 30 с:
а) 3 с; б) 3; в) 3 мин; г) свой ответ
-
Из данных пропорций выберите верные:
1) 43:43=23:23; 2) 38:26=83:73;
3) 20:4=30:4; 4) 55:5=0:15;
5) 14,2:3,55=31,2:7,8; 6) 17,96:8,88=34,12:14,4
а) 1, 4, 5; б) 1, 5; в) 2, 3, 6; г) свой ответ
-
Найдите неизвестный член пропорции: 10,5:х=7:
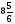
а) 5,25; б) 0,5; в) 0,05; г) свой ответ
-
За 5 ч автомобиль проехал 62,5% всего пути. Сколько времени ему потребуется на оставшуюся часть пути?
а) 8 ч; б) 3 ч; в) 5 ч; г) свой ответ
-
Из нефти получается 6% бензина. Сколько нефти требуется для получения 4,2 т бензина?
а) 7 т; б) 70 т; в) 12,6 т; г) свой ответ
-
Длина реки на местности составляет 125 км, а на карте
5 см. Определите масштаб карты.
а) 1:2500000; б) 1:250000; в) 1:400000; г) свой ответ
-
Найдите площадь окружности, диаметр которой равен
68 см.
а) 28,26 см2; б) 56,52 см2;
в) 4,71 см2; г) свой ответ
-
Колесо автобуса, диаметр которого 1,2 м, сделало 200 оборотов. Какое расстояние проехал автобус? Ответ выразите в метрах.
а) 188,4 м; б) 376,8 м; в) 753,6 м; г) свой ответ
-
Сумма двух чисел составляет 225% первого слагаемого. На сколько процентов первое слагаемое меньше второго?
а) на 25%; б) на 125%;
в) на 20%; г) свой ответ
ТЕСТ №4
Тема: Отношения и пропорции
Вариант 4
-
Какое из данных отношений равно
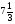 :
:
а) 5:7; б) 7:2; в) 26,6619; г) свой ответ
-
Найдите отношение 360 л к 3 м3:
а) 12; б) 0,12 ; в) 1,2; г) свой ответ
-
Из данных пропорций выберите верные:
1) 84:79=94:84; 2) 46:23=23:46;
3) 32:10=12,8:4; 4) 12,8:1,6=33,2:0,4;
5) 67:2=16,75:0,5; 6) 53:53=27:27
а) 6, 3, 5; б) 1, 3; в) 5, 6, 4; г) свой ответ
-
Найдите неизвестный член пропорции: 3,6:х=0,012:0,01
а) 3; б) 0,3; в) 0,012; г) свой ответ
-
Трактор вспахал 35% поля за 7 часов. Сколько времени потребуется трактору, чтобы вспахать оставшуюся часть поля?
а) 20 ч; б) 13 ч; в) 7 ч; г) свой ответ
-
Из яблок получается 24% сока. Сколько яблок требуется для получения 0,6 т сока?
а) 25 т; б) 2,5 т; в) 1,9 т; г) свой ответ
-
Длина озера на местности составляет 2,7 км, а на карте 5,4 см. Определите масштаб карты.
а) 1:20000; б) 1:5000; в) 1:50000; г) свой ответ
-
Найдите площадь окружности, диаметр которой равен
7 дм.
а) 5,495 дм2; б) 38,465 дм2;
в) 76,93 дм2; г) свой ответ
-
Найдите диаметр окружности, если ее длина 226,08 м. Ответ выразите в дециметрах.
а) 72 дм; б) 36 дм; в) 720 дм; г) свой ответ
-
Разность двух чисел составляет 62,5% уменьшаемого. На сколько процентов уменьшаемое больше вычитаемого?
а) на 37,5%; б) на 62,5%;
в) на 375%; г) свой ответ
ТЕСТ №5
Тема: Положительные и отрицательные числа.
Вариант 1
-
Бельчонок путешествует по координатной прямой, на которой отмечены точки А(-2), B(5), C(3), D(-7). Какой из его маршрутов самый короткий?
а) ABCD; б) ACBD; в) ADCB; г) ADBC
-
Укажите все пары противоположных чисел:
1) - ( - 6) и 6; 2) - ( - 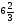 ) и
) и 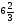 ;
;
3) 12 и 12; 4) 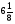 и
и 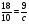 ;
;
5) 6,5 и - 6,5; 6) 1,25 и 0,8
а) 1, 2, 5; б) 2 и 5; в) 5; г) свой ответ
-
Сколько целых чисел расположено на координатной прямой между числами - 7 и 8?
а) 13; б) 14; в) 15; г) свой ответ
-
Расположите числа a= -6,7; b=
 ; c=-12 в порядке возрастания их модуля.
; c=-12 в порядке возрастания их модуля.
а) a, b, c; б) b, a, c; в) a, c, b; г) свой ответ
-
Какое из данных чисел наибольшее?
а) -876,89; б) 16,098; в) 4,45; г) 16,65
-
Костя выше Кирилла на 7 см, Кирилл выше Саши на 3 см, а Саша ниже Олега на 8 см. Кто из ребят самый высокий?
а) Костя; б) Кирилл; в) Саша; г) Олег
-
Выполните действие |-9,67|+|-7,8|
а) 1,87; б) -1,87; в) 17,47; г) свой ответ
-
Выполните действия |-3,78| : |-1,5| · |-2,1|
а) 1,2; б) -1,2; в) 1,8; г) свой ответ
-
Найдите среднее арифметическое чисел |-х| и |у|, если х=4,5 и у=6,6
а) 5,55; б) 11,1; в) 5,45; г) свой ответ
-
Решите уравнение |5-х| = 2
а) 3 и -3; б) 7 и -7; в) 3 и 7; г) свой ответ
ТЕСТ №5
Тема: Положительные и отрицательные числа.
Вариант 2
-
Щенок путешествует по координатной прямой, на которой отмечены точки А(-5), B(4), C(6), D(-8). Какой из его маршрутов самый короткий?
а) ABCD; б) ACBD; в) ADCB; г) ADBC
-
Укажите все пары противоположных чисел:
1) - 4 и 4; 2) 2,5 и 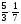 ;
;
3) 12 и -(-12); 4) -1 и -(-(-1));
5) 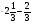 и -
и -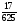 ; 6) 1,25 и 0,8
; 6) 1,25 и 0,8
а) 1, 2, 5; б) 2 и 5; в) 5; г) свой ответ
-
Сколько целых чисел расположено на координатной прямой между числами - 3 и 9?
а) 13; б) 12; в) 11; г) свой ответ
-
Расположите числа a= -4,6; b=
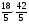 ; c=2 в порядке возрастания их модуля.
; c=2 в порядке возрастания их модуля.
а) a, b, c; б) b, a, c; в) a, c, b; г) свой ответ
-
Какое из данных чисел наименьшее?
а) -99,89; б) 1,098; в) -100,15; г) 21,45
-
Настя выше Кати на 5 см, Катя ниже Саши на 3 см, а Саша ниже Ольги на 8 см. Кто из девочек самая высокая?
а) Настя; б) Катя; в) Саша; г) Ольга
-
Выполните действие |6,25|+|-2,34|
а) 8,59; б) -3,91; в) 3,91; г) свой ответ
-
Выполните действия |-2,76| : |-2,3| · |-3,11|
а) 37,32; б) -3,372; в) 3,732; г) свой ответ
-
Найдите среднее арифметическое чисел |-х| и |у|, если х=2,8 и у=-4,6
а) -3,7; б) 7,4; в) 3,7; г) свой ответ
-
Решите уравнение |3-х| = 2
а) 1 и -1; б) 1 и 5; в) 5 и -5; г) свой ответ
ТЕСТ №5
Тема: Положительные и отрицательные числа.
Вариант 3
-
Бельчонок путешествует по координатной прямой, на которой отмечены точки А(-6), B(-5), C(2), D(-1). Какой из его маршрутов самый короткий?
а) ABCD; б) ACBD; в) ADCB; г) ADBC
-
Укажите все пары противоположных чисел:
1) - ( - 3) и 3; 2) 3,5 и -3,5;
3) 1 и 1,001; 4) 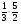 и
и 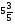 ;
;
5) -2 и -(-(-2)); 6) -1,2 и 0,9
а) 1, 2, 5, 4; б) 2 и 5; в) 2, 4; г) свой ответ
-
Сколько целых чисел расположено на координатной прямой между числами - 4 и 4?
а) 10; б) 9; в) 8; г) свой ответ
-
Расположите числа a= -3,1; b=
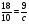 ; c=1 в порядке возрастания их модуля.
; c=1 в порядке возрастания их модуля.
а) a, b, c; б) b, a, c; в) a, c, b; г) свой ответ
-
Какое из данных чисел наибольшее?
а) -75,854; б) 78,0543; в) 78,543; г) -99,43
-
Костя выше Вити на 1 см, Кирилл выше Кости на 8 см, а Витя ниже Олега на 10 см. Кто из ребят самый высокий?
а) Костя; б) Кирилл; в) Витя; г) Олег
-
Выполните действие |-5,93| - |-2,18|
а) 3,75; б) -8,11; в) 8,11; г) свой ответ
-
Выполните действия |-3,32| · |-5,4| : |-2,4|
а) 7,47; б) -7,47; в) 74,7; г) свой ответ
-
Найдите среднее арифметическое чисел |-х| и |у|, если
х=-6,54 и у=-7,2
а) -6,87; б) 13,74; в) 6,87; г) свой ответ
-
Решите уравнение |х-6| = 2
а) 17 и -1; б) 17 и 1; в) -17 и -1; г) свой ответ
ТЕСТ №5
Тема: Положительные и отрицательные числа.
Вариант 4
-
Щенок путешествует по координатной прямой, на которой отмечены точки А(2), B(-4), C(6), D(-3). Какой из его маршрутов самый короткий?
а) ABCD; б) ACBD; в) ADCB; г) ADBC
-
Укажите все пары противоположных чисел:
1) 3,4 и -3,4; 2) 3,5 и -4,5;
3) -1 и -(-1); 4) 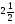 и
и 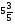 ;
;
5) -5 и -(-(-5)); 6) -11,2 и 11,9
а) 1, 2, 5, 4; б) 3; в) 3, 5; г) свой ответ
-
Сколько целых чисел расположено на координатной прямой между числами - 6 и 5?
а) 11; б) 12; в) 13; г) свой ответ
-
Расположите числа a= -2,01; b=
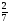 ; c=3 в порядке возрастания их модуля.
; c=3 в порядке возрастания их модуля.
а) a, b, c; б) b, a, c; в) a, c, b; г) свой ответ
-
Какое из данных чисел наименьшее?
а) 56,87; б) -76,98; в) -98,76; г) 98,876
-
Настя выше Кати на 3 см, Катя выше Ани на 2 см, а Аня ниже Ольги на 4 см. Кто из девочек выше всех?
а) Настя; б) Катя; в) Аня; г) Ольга
-
Выполните действие |-9,92| - |-7,46|
а) 2,46; б) 17,38; в) -17,38; г) свой ответ
-
Выполните действия |-2,85| · |-3,2| : |-1,2|
а) -7,6; б) 7,6; в) 0,76; г) свой ответ
-
Найдите среднее арифметическое чисел |-х| и |у|, если х=6,38 и у=-4,8
а) 5,59; б) 11,18; в) -5,59; г) свой ответ
-
Решите уравнение |х+4| = 12
а) 8 и -16; б) -8 и 17; в) 6 и -8; г) свой ответ
ТЕСТ №6
Тема: Сложение положительных и отрицательных чисел
Вариант 1
-
Какой из данных примеров решен верно?
а) -2,3+(-7,4)=-5,1; б) 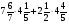 ;
;
в) 2,3+(-7,4)=5,1; г) 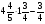
-
Какой из данных примеров решен верно?
а) -2,3-(-7,4)=5,1; б) 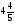 ;
;
в) -2,3-(-7,4)=9,7; г) -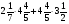
-
Найдите значение выражения 4,3-(0,43+с) при
с=-2,3
а) 6,17; б) 1,57; в) 2,43; г) свой ответ
-
Решите уравнение х-4,6=-9,3
а) 4,7; б) -4,7; в) -13,9; г) свой ответ
-
Решите уравнение -у+2,92=0,3
а) 2,62; б) 3,22; в) -2,62; г) свой ответ
-
Вычислите: -1+2-(-3)+(-4)-5
а) 12; б) 2; в) 5; г) свой ответ
-
Найдите значение выражения: 0,45-х-3,8
при х=-1,38
а) 6,92; б) -1,97; в) -4,73; г) свой ответ
-
Вася задумал число, прибавил к нему 67, затем от результата отнял 60. В результате у него получилось число -98. Какое число задумал Вася?
а) -105; б) 19; в) -19; г) свой ответ
-
Решите уравнение: |х+2|=5
а) 5 и -5; б) 3 и -7; в) -7 и 5; г) свой ответ
-
Найдите сумму всех целых чисел n таких, что
-17<n<14
а) -48; б) -31; в) 31; г) свой ответ
ТЕСТ №6
Тема: Сложение положительных и отрицательных чисел
Вариант 2
-
Какой из данных примеров решен верно?
а) 6,5+(-2,3)=3,3; б) 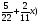 ;
;
в) -8,25+(-3,36)=-11,61; г) 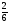
-
Какой из данных примеров решен верно?
а) 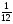 ; б) -2,8-6,5=-9,3;
; б) -2,8-6,5=-9,3;
в) 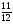 ; г) -9,2-6,4=2,8
; г) -9,2-6,4=2,8
-
Найдите значение выражения 5,6-(2,4+с) при
с=1,4
а) 2,7; б) 1,8; в) 0,43; г) свой ответ
-
Решите уравнение х-5,15=1,1
а) 6,25; б) -5,85; в) 5,75; г) свой ответ
-
Решите уравнение -х+5,18=11,58
а) 6,4; б) -4,5; в) -6,4; г) свой ответ
-
Вычислите: -1+3-5+7-(-9)+(-11)
а) 12; б) 2; в) 5; г) свой ответ
-
Найдите значение выражения: 6,5-3,4-х
при х=-2,7
а) -0,4; б) 0,4; в) 5,8; г) свой ответ
-
Вася задумал число, прибавил к нему 45, затем от результата отнял 87. В результате у него получилось число -14. Какое число задумал Вася?
а) 28; б) 73; в) -19; г) свой ответ
-
Решите уравнение: |у-3|=6
а) 9 и -3; б) 3 и -9; в) -3 и 6; г) свой ответ
-
Найдите сумму всех целых чисел n таких, что
-13,5<n<11
а) -48; б) -36; в) 36; г) свой ответ
ТЕСТ №6
Тема: Сложение положительных и отрицательных чисел
Вариант 3
-
Какой из данных примеров решен верно?
а) -6,7+(-2,8)=-9,5; б) 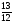 ;
;
в) 9,2+(-6,4)=2,9; г) 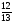
-
Какой из данных примеров решен верно?
а) 9,9-6,25=3,65; б) 6,8-(-4,2)=2,6;
в) 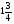 ; г) -
; г) -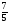
-
Найдите значение выражения с-(2,4-3,5) при
с=-2,7
а) 3,5; б) 1,8; в) -1,6; г) свой ответ
-
Решите уравнение 9,6-х=4,22
а) 4,32; б) -3,68; в) 5,65; г) свой ответ
-
Решите уравнение х+4,5=-3,1
а) 3,4; б) -7,2; в) -1,4; г) свой ответ
-
Вычислите: 2+4-6+8+(-10)-(-12)
а) 10; б) 8; в) 12; г) свой ответ
-
Найдите значение выражения: 8,65-(-(-х))-4,2
при х=2,34
а) -2,14; б) 2,11; в) 6,79; г) свой ответ
-
Вася задумал число, прибавил к нему 23, затем от результата отнял 145. В результате у него получилось число -76. Какое число задумал Вася?
а) 46; б) -23; в) 69; г) свой ответ
-
Решите уравнение: |х+6|=11
а) 5 и -5; б) 4 и -17; в) -11 и 5; г) свой ответ
-
Найдите сумму всех целых чисел n таких, что
-10<n<12,3
а) 48; б) -33; в) 33; г) свой ответ
ТЕСТ №6
Тема: Сложение положительных и отрицательных чисел
Вариант 4
-
Какой из данных примеров решен верно?
а) -8,97+6,25=15,22; б) 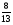 ;
;
в) 5,56+(-6,3)=0,74; г) 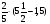
-
Какой из данных примеров решен верно?
а) -8,5-3,4=5,1; б) 7,89-(-6,35)=1,54;
в) 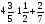 ; г)
; г) 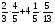
-
Найдите значение выражения с+(5,32-2,56) при
с=-1,9
а) 0,86; б) -1,87; в) 2,5; г) свой ответ
-
Решите уравнение -2,4-х=5,43
а) 7,83; б) -2,17; в) 9,25; г) свой ответ
-
Решите уравнение х+(-2,6)=5,82
а) -2,24; б) -4,62; в) 8,42; г) свой ответ
-
Вычислите: -10+(-11)+12+13+(-14)+15+(-16)
а) -10; б) -11; в) -12; г) свой ответ
-
Найдите значение выражения: 6,75+(-х)-4,6
при х=-2,3
а) -0,15; б) 4,45; в) -1,25; г) свой ответ
-
Вася задумал число, прибавил к нему 12, затем от результата отнял 37. В результате у него получилось число -32. Какое число задумал Вася?
а) 5; б) -7; в) 12; г) свой ответ
-
Решите уравнение: |у-2|=6
а) 8 и -4; б) -8 и 4; в) 5 и -11; г) свой ответ
-
Найдите сумму всех целых чисел n таких, что
-20<n<16,3
а) -54; б) -33; в) -74; г) свой ответ
ТЕСТ № 7
Тема: Умножение и деление положительных и отрицательных чисел
Вариант 1
-
Какие из данных примеров решены верно?
а) -2,7·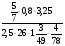 =-3,9; б) -2,17· (-1,5)=-3,255;
=-3,9; б) -2,17· (-1,5)=-3,255;
в) 3,01· (-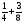 )=-0,43; г)
)=-0,43; г) 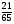
-
Какие из данных примеров решены верно?
а) -7,112 : (-5,6)=-1,27; б) -1,21 : (-1,1)=-1,1;
в) 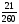 :
: 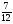 ; г)
; г) 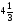 :
: 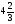 =-2,5
=-2,5
-
Решите уравнение: х · (-3,45)=5,865
а) -0,17; б) -1,7; в) 1,7; г) 0,17
-
Решите уравнение: у : 2,34=-6,1
а) 14,274; б) -14,274; в) 142,74; г) свой ответ
-
Представьте в виде десятичной дроби число
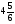
а) 0,(272); б) 0,2(72); в) 0,2727272; г) свой ответ
-
Выполните действия: -2,5 · (-1,6)+41,6 : (-4)
а) 6,4; б) -0,64; в) 0,64; г) свой ответ
-
Найдите значение выражения m2-1,3 при m=-1,3
а) 1,49; б) -2,99; в) 0,39; г) свой ответ
-
Выполните действия:
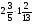
а) 1,5; б) -1,5; в) 15; г) свой ответ
-
Выполните действия:
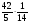
а) 10; б) -10; в) 1; г) свой ответ
-
Решите уравнение: (-х+3) · (х+4)=0
а) -3 и -4; б) 3 и -4; в) -3 и 4; г) свой ответ
ТЕСТ № 7
Тема: Умножение и деление положительных и отрицательных чисел
Вариант 2
-
Какие из данных примеров решены верно?
а) 1,25 · (-2,3)=2,875; б) -4,3 · 6,21=26,703;
в) 3,2 · 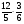 =6,8; г)
=6,8; г) 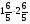
-
Какие из данных примеров решены верно?
а) -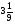 : (-
: (-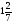 )=-
)=- 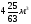 б) 4,8 : 1,2=0,4;
б) 4,8 : 1,2=0,4;
в) -2,25 : 1,5=1,5; г)  : 2,8=1
: 2,8=1
-
Решите уравнение: -х · (-1,12)=4,032
а) -0,36; б) -3,6; в) 3,6; г) 0,36
-
Решите уравнение: - у : 1,56=-4,5
а) 7,02; б) -7,02; в) 70,2; г) свой ответ
-
Представьте в виде десятичной дроби число
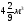
а) 0,(227); б) 0,2272727; в) 0,2(27); г) свой ответ
-
Выполните действия: 2,4 · (-1,2)+4,8 : (-2,4)
а) 8,2; б) -0,88; в) -8,2; г) свой ответ
-
Найдите значение выражения -m2+12,8 при m=-3,1
а) -3,19; б) 22,41; в) 3,19; г) свой ответ
-
Выполните действия:
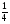
а) 9,6; б) -9,6; в) -0,96; г) свой ответ
-
Выполните действия:
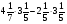
а) 10; б) -10; в) 1; г) свой ответ
-
Решите уравнение: (х+2) · (-х+5)=0
а) -2 и -5; б) 2 и -5; в) -2 и 5; г) свой ответ
ТЕСТ № 7
Тема: Умножение и деление положительных и отрицательных чисел
Вариант 3
-
Какие из данных примеров решены верно?
а) 7,8 ·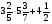 =-17; б) -4,3 · 2,5=10,75;
=-17; б) -4,3 · 2,5=10,75;
в) -6,5 · (-0,25)=-1,625; г) 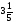
-
Какие из данных примеров решены верно?
а) -3,6 : (-1,2)=-2,4; б) -6,25 : 2,5=-2,5;
в) 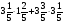 : (
: (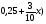 ; г)
; г) 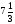 :
: 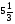
-
Решите уравнение: х · 2,6=-17,03
а) 6,55; б) 1,6; в) -5,65; г) -6,55
-
Решите уравнение: 17,55 : у=-6,5
а) -2,8; б) -2,7; в) 2,9; г) свой ответ
-
Представьте в виде десятичной дроби число
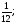
а) 0,6(25); б) 0,62(5); в) 0,(625); г) свой ответ
-
Выполните действия: 3,4 · 1,2+4,6 · (-2,2)
а) 6,04; б) -0,64; в) -6,04; г) свой ответ
-
Найдите значение выражения m2+2,4 при m=-1,3
а) 4,09; б) 3,22; в) 0,71; г) свой ответ
-
Выполните действия:
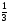
а) 4,8; б) -9,6; в) 9,6; г) свой ответ
-
Выполните действия:
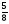
а) 14,4; б) 1,44; в) 0,144; г) свой ответ
-
Решите уравнение: (х-3) · (-х+5)=0
а) -3 и -5; б) 3 и -5; в) 3 и 5; г) свой ответ
ТЕСТ № 7
Тема: Умножение и деление положительных и отрицательных чисел
Вариант 4
-
Какие из данных примеров решены верно?
а) 2,5 ·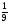 =-12; б)
=-12; б) 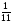 ;
;
в) 0,25· 6,4=1,6; г) -3,8 · 5,6=21,28
-
Какие из данных примеров решены верно?
а) -5,6 : 2,8=-0,2; б) 1,1 : 0,2=-5,5;
в) 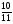 :
: 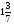 ; г)
; г) 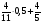 :
: 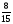
-
Решите уравнение: -х · (-4,5)=-16,02
а) 3,56; б) -3,56; в) 35,6; г) -35,6
-
Решите уравнение: 1,69 : (-х)=1,3
а) 1,4; б) -1,4; в) -1,3; г) свой ответ
-
Представьте в виде десятичной дроби число
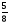
а) 0,(6); б) 0,6666667; в) 0,667; г) свой ответ
-
Выполните действия: 3,8 · (-6,5)+5,8 · 5,6
а) 5,48; б) -6,7; в) 7,78; г) свой ответ
-
Найдите значение выражения 3,4-m2 при m=-2,3
а) -1,89; б) 2,21; в) 1,29; г) свой ответ
-
Выполните действия:
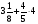
а) 3,5; б) -3,5; в) 4,8; г) свой ответ
-
Выполните действия:
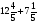
а) 8; б) 9; в) 10; г) свой ответ
-
Решите уравнение: (4-х) · (х+5)=0
а) 4 и -5; б) -5 и -4; в) 5 и 4; г) свой ответ
ТЕСТ №8
Тема: Решение уравнений
Вариант 1
-
Упростите выражение: х - (х-у)
а) 2х - у; б) у; в) -у; г) свой ответ
-
Выполните действия: (2,5 - 3,8) - (3,4 - 5,6)
а) -10,3; б) -3,5; в) 0,9; г) свой ответ
-
Найдите коэффициент в произведении 3,5х · (-
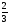 у2)
у2)
а) 2ху2; б) -2; в)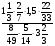 ; г) свой ответ
; г) свой ответ
-
Приведите подобные слагаемые: -9х+3у+4х+у
а) -5ху; б) 4у-5х; в) 4у-13х; г) свой ответ
-
Выполните действия:
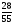 )
)
а) -3; б) -3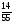 ; в) -2; г) свой ответ
; в) -2; г) свой ответ
-
Вася задумал натуральное число. Если к нему приписать справа 5, то оно увеличится на 437. Какое число задумано?
а) -48; б) 49; в) 42; г) свой ответ
-
Решите уравнение:
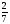
а) -2; б) 2; в) -98; г) свой ответ
-
Отец в два раза старше сына и на 25 лет старше дочери. Сколько лет дочери, если всем вместе 95 лет?
а) 23; б) 24; в) 48; г) свой ответ
-
Упростите выражение: 5а - (6а - (7а - (8а - 9)))
а) 9 - 2а; б) 9 - 21а; в) -9 - 2а; г) свой ответ
-
Решите уравнение: 5 · (4 - 3х) - 4 · (7 - 4х) = 1,3
а) 0,3; б) 9,3; в) -6,7; г) свой ответ
ТЕСТ №8
Тема: Решение уравнений
Вариант 2
-
Упростите выражение: -х+у - (у - х)
а) 0; б) 2у; в) 2х; г) свой ответ
-
Выполните действия: (5,74+8,27) - (3,4 +3,78)
а) 6,83; б) -6,83; в) 6,9; г) свой ответ
-
Найдите коэффициент в произведении
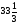 х · (-2,3х)
х · (-2,3х)
а) -2,3х; б) -2,3; в)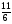 ; г) свой ответ
; г) свой ответ
-
Приведите подобные слагаемые: 3х+4у - 4х - (-у)
а) х+3у; б) -х+5у; в) -х+3у; г) свой ответ
-
Выполните действия:
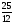
а) -4,2; б) -3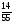 ; в) 5,37; г) свой ответ
; в) 5,37; г) свой ответ
-
Петя задумал натуральное число. Если к нему приписать справа 2, то оно увеличится на 180. Какое число задумано?
а) -43; б) 45; в) 42; г) свой ответ
-
Решите уравнение:

а) 10,2; б) 25,3; в) -11,4; г) свой ответ
-
Отец в 2,5 раза старше сына и на 24 года старше дочери. Сколько лет сыну, если всем вместе 93 года?
а) 41; б) 65; в) 26; г) свой ответ
-
Упростите выражение: 6а - (-3а - (-2а))+5
а) 5а+5; б) а+5; в) -11а+5; г) свой ответ
-
Решите уравнение: 6 · (2х+3) - 4 · (2х-4) = 0
а) -0,5; б) 0,5; в) 1,5; г) свой ответ
ТЕСТ №8
Тема: Решение уравнений
Вариант 3
-
Упростите выражение: (у - х) - (х-у)
а) 2х - 2у; б) 0; в) 2у-2х; г) свой ответ
-
Выполните действия: (3,45 - 2,78)+ (2,34+4,5)
а) 1,67; б) -1,67; в) 6,17; г) свой ответ
-
Найдите коэффициент в произведении -6,8х · (-
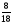 у2)
у2)
а) -6,8; б) 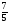 ; в) -6ху2; г) свой ответ
; в) -6ху2; г) свой ответ
-
Приведите подобные слагаемые: -5х+3у+2х-у
а) 7х+2у; б) -3х+4у; в) -3х+2у; г) свой ответ
-
Выполните действия:
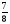
а) -3; б) 3; в) 0,3; г) свой ответ
-
Коля задумал натуральное число. Если к нему приписать справа 3, то оно увеличится на 37. Какое число задумано?
а) -60; б) 58; в) 59; г) свой ответ
-
Решите уравнение:
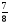
а) 0,5; б) -0,5; в) 1,5; г) свой ответ
-
Отец в 3 раза старше сына и на 20 лет старше дочери. Сколько лет дочери, если всем вместе 100 лет?
а) 60; б) 20; в) 40; г) свой ответ
-
Упростите выражение: 7+6х - (5х+3 - (4х))
а) 15х+10; б) 5х+4; в) 10-3х; г) свой ответ
-
Решите уравнение: 3 · (2х+3) + 4 · (5-х) = 43
а) 5; б) -6; в) 7; г) свой ответ
ТЕСТ №8
Тема: Решение уравнений
Вариант 4
-
Упростите выражение: (2х-у)+(у-х)-у
а) 2х - у; б) х+у; в) -х; г) свой ответ
-
Выполните действия: (6,28+3,56) - (9,45-1,23)
а) 1,62; б) -0,84; в) -1,62; г) свой ответ
-
Найдите коэффициент в произведении
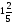 х · (-2,2у)
х · (-2,2у)
а) -2,2х; б) 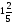 ; в) 7,04; г) свой ответ
; в) 7,04; г) свой ответ
-
Приведите подобные слагаемые: -6х+4у+8х-2у
а) 2х+2у; б) 14х+2у; в) 2х+6у; г) свой ответ
-
Выполните действия:
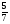
а) 5,15; б) -5,15; в) 5,25; г) свой ответ
-
Вася задумал натуральное число. Если к нему приписать справа 8, то оно увеличится на 116. Какое число задумано?
а) -10; б) 16; в) 12; г) свой ответ
-
Решите уравнение:
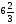
а) -5,7; б) 6,34; в) 7,4; г) свой ответ
-
Отец в 1,5 раза старше сына и на 24 года старше дочери. Сколько лет дочери, если всем вместе 95 лет?
а) 51; б) 34; в) 27; г) свой ответ
-
Упростите выражение: 2х-3+(5-6х-(-3х))
а) -х-2; б) 2-х; в) 2-7х; г) свой ответ
-
Решите уравнение: 8 · (3-х) - 5 · (4-2х) = 8
а) 8; б) 10; в) -8; г) свой ответ
ТЕСТ №9
Тема: Координаты на плоскости
Вариант 1
-
На каком из рисунков изображены перпендикулярные прямые?
а) б)
в) г)
-
На каком из рисунков изображены параллельные прямые? (см. задание 1)
-
Координаты точек A(-1;2), B(3;4). В какой точке отрезок AB пересекает ось абсцисс?
а) (0; -5); б) (0; 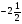 ); в) (-5; 0); г) свой ответ
); в) (-5; 0); г) свой ответ
-
Какие из данных точек расположены выше оси абсцисс: A(2; 4); B(3; -1); C(0; 2); D(4; 0)?
а) A, B, D; б) A, C; в) B, D г) свой ответ
-
Найдите площадь прямоугольника с вершинами в точках:
A(-1; 2); B(4; 2); C(4; -2); D(-1; -2)
а) 20; б) 10; в) 12; г) свой ответ
-
Отметьте на координатной плоскости точки A(-5; 7);
B(1; 5); C(4; 2); D(-1; -1). На какой из прямых лежит точка K(3; 3)?
а) AB; б) BC; в) CD; г) AD
-
Измерьте длину отрезка AB, если A(-3; 2); B(1; -1). Длина единичного отрезка - 1 см.
а) 3; б) 4; в) 5; г) свой ответ
-
Чему равна величина угла ABC, если A(-2; 3); B(1; 2); C(5;4)?
а) 45º; б) 135º; в) 120º; г) свой ответ
-
Найдите длину окружности с диаметром MN,
если M(-1; 2); N(3; 2).
а) 6,28; б) 12,56; в) 25,12; г) свой ответ
-
Чему равна площадь треугольника с вершинами A(1; 3); B(2; -2); C(-2; -2)?
а) 10; б) 20; в) 12; г) свой ответ
ТЕСТ №9
Тема: Координаты на плоскости
Вариант 2
-
На каком из рисунков изображены перпендикулярные прямые?
а) б)
в) г)
-
На каком из рисунков изображены параллельные прямые? (см. задание 1)
-
Координаты точек A(-2; -5), B(4; 4). В какой точке отрезок AB пересекает ось ординат?
а) (-2; 0); б) (0; -2); в) (1,5; 0); г) свой ответ
-
Какие из данных точек расположены выше оси абсцисс: A(1; 2); B(1; -1); C(-3; -2); D(-2; 1)?
а) A, D; б) A, C; в) B, D г) свой ответ
-
Найдите площадь прямоугольника с вершинами в точках:
A(-1; 1); B(3; 1); C(3; -2); D(-1; -2)
а) 20; б) 10; в) 12; г) свой ответ
-
Отметьте на координатной плоскости точки A(-1; 4);
B(5; 2); C(2; -1); D(-2; -2). На какой из прямых лежит точка K(2; 3)?
а) AB; б) BC; в) CD; г) AD
-
Измерьте длину отрезка AB, если A(-2; 4); B(6; -2). Длина единичного отрезка - 1 см.
а) 8; б) 10; в) 12; г) свой ответ
-
Чему равна величина угла ABC, если A(2; 4); B(-1; 1); C(3;1)?
а) 45º; б) 90º; в) 75º; г) свой ответ
-
Найдите длину окружности с диаметром MN,
если M(-2; -2); N(1; 2).
а) 15,7; б) 7,85; в) 31,4; г) свой ответ
-
Чему равна площадь треугольника с вершинами A(5; 3); B(5; -4); C(0; -3)?
а) 12,5; б) 25; в) 12; г) свой ответ
ТЕСТ №9
Тема: Координаты на плоскости
Вариант 3
-
На каком из рисунков изображены перпендикулярные прямые?
а) б)
в) г)
-
На каком из рисунков изображены параллельные прямые? (см. задание 1)
-
Координаты точек A(8; 2), B(-4; -1). В какой точке отрезок AB пересекает ось ординат?
а) (0; 0); б) (1; 0); в) (0; 1); г) свой ответ
-
Какие из данных точек расположены правее оси ординат: A(-1; 2); B(2; 3); C(2; -3); D(-2; -1)?
а) A, D; б) A, C; в) B, D г) свой ответ
-
Найдите площадь прямоугольника с вершинами в точках:
A(-2; 2); B(4; 2); C(4; -1); D(-2; -1)
а) 18; б) 16; в) 20; г) свой ответ
-
Отметьте на координатной плоскости точки A(-1; 3);
B(2; 2); C(4; 2); D(-2; -2). На какой из прямых лежит точка K(1; 0)?
а) AB; б) BC; в) CD; г) AD
-
Измерьте длину отрезка AB, если A(-4; 5); B(5; -7). Длина единичного отрезка - 1 см.
а) 10; б) 15; в) 12; г) свой ответ
-
Чему равна величина угла ABC, если A(1; -3); B(3; 3); C(-2; -2)?
а) 45º; б) 30º; в) 15º; г) свой ответ
-
Найдите длину окружности с диаметром MN,
если M(-3; 4); N(3; -4).
а) 15,7; б) 7,85; в) 31,4; г) свой ответ
-
Чему равна площадь треугольника с вершинами A(4; 2); B(4; -2); C(-2; 1)?
а) 6; б) 24; в) 12; г) свой ответ
ТЕСТ №9
Тема: Координаты на плоскости
Вариант 4
-
На каком из рисунков изображены перпендикулярные прямые?
а) б)
в) г)
-
На каком из рисунков изображены параллельные прямые? (см. задание 1)
-
Координаты точек A(-1; 4), B(3; -4). В какой точке отрезок AB пересекает ось абсцисс?
а) (0; 0); б) (1; 0); в) (0; 1,5); г) свой ответ
-
Какие из данных точек расположены правее оси ординат: A(1; -2); B(-2; -1); C(-1; 1); D(4; 1)?
а) A, D; б) A, C; в) B, D г) свой ответ
-
Найдите площадь прямоугольника с вершинами в точках:
A(-1; 4); B(2; 4); C(2; -1); D(-1; -1)
а) 10; б) 15; в) 20; г) свой ответ
-
Отметьте на координатной плоскости точки A(-1; 6);
B(1; 4); C(2; 1); D(-3; -2). На какой из прямых лежит точка K(-2; -2)?
а) AB; б) BC; в) CD; г) AD
-
Измерьте длину отрезка AB, если A(-2; 8); B(3; -4). Длина единичного отрезка - 1 см.
а) 13; б) 14; в) 15; г) свой ответ
-
Чему равна величина угла ABC, если A(-1; -4); B(1; 2); C(-2; 3)?
а) 60º; б) 30º; в) 90º; г) свой ответ
-
Найдите длину окружности с диаметром MN,
если M(-3; 6); N(2; -6).
а) 40,82; б) 20,41; в) 10,205; г) свой ответ
-
Чему равна площадь треугольника с вершинами A(4; 2); B(4; -2); C(-2; 1)?
а) 10; б) 12; в) 14; г) свой ответ
ИТОГОВЫЙ ТЕСТ
Вариант 1
-
Найдите значение выражения:
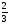
а) 9,6; б) 10,6; в) 12,2; г) свой ответ
-
За 2,5 часа автомобиль прошел 145 км. За какое время автомобиль пройдет 261 км, если будет двигаться с той же средней скоростью?
а) 4,3 ч; б) 4,4 ч; в) 4,5 ч; г) свой ответ
-
Решите уравнение:
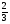
а) 19,2; б) 17,6; в) 15,3; г) свой ответ
-
Какую цифру следует поставить вместо в число 9425, чтобы полученное число делилось на 12?
а) 2; б) 6; в) 8; г) свой ответ
-
Теплоход за три дня прошел 595 км. В первый день он прошел
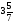 пути, а во второй- 45% оставшегося пути. Какое расстояние он прошел за третий день?
пути, а во второй- 45% оставшегося пути. Какое расстояние он прошел за третий день?
а) 187 км; б) 12,25 км; в) 122,5 км; г) свой ответ
-
Найдите число, 12% которого равны 240.
а) 28,8; б) 2000; в) 320; г) свой ответ
-
Упростите выражение: 7· (2а-4,2)-(4+а)
а) 15а-33,4; б) 13а-25,4; в) 13а-33,4; г) свой ответ
-
Длина окружности равна 20 см. Найдите ее диаметр. Ответ округлите до сотых.
а) 12,74; б) 25,47; в) 25,48; г) свой ответ
-
Найдите координаты середины отрезка AB, если
A(-4; -1); B(8; 3)
а) (2; 1); б) (-2; 1); в) (2; -1); г) свой ответ
-
Какова последняя цифра числа:
172+133+2 · 3 · … · 88?
а) 1; б) 0; в) 5; г) свой ответ
ИТОГОВЫЙ ТЕСТ
Вариант 2
-
Найдите значение выражения:
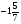
а) 1,15; б) 2,5; в) -2,3; г) свой ответ
-
За 3,5 часа автомобиль прошел 238 км. За какое время автомобиль пройдет 578 км, если будет двигаться с той же средней скоростью?
а) 8,3 ч; б) 8,4 ч; в) 8,5 ч; г) свой ответ
-
Решите уравнение:
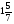
а) 8,65; б) 7,32; в) 6,55; г) свой ответ
-
Какую цифру следует поставить вместо в число 3566, чтобы полученное число делилось на 9?
а) 1; б) 3; в) 5; г) свой ответ
-
Теплоход за три дня прошел 675 км. В первый день он прошел
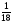 пути, а во второй- 32% оставшегося пути. Какое расстояние он прошел за третий день?
пути, а во второй- 32% оставшегося пути. Какое расстояние он прошел за третий день?
а) 234 км; б) 128,5 км; в) 351 км; г) свой ответ
-
Найдите число, 37% которого равны 518.
а) 576,65; б) 1400; в) 14; г) свой ответ
-
Упростите выражение: 6· (х+8,5)-4· (6,4+х)
а) 2х+25,4; б) 10х+25,4; в) 10х+76,4; г) свой ответ
-
Длина окружности равна 14 см. Найдите ее диаметр. Ответ округлите до сотых.
а) 2,23; б) 4,46; в) 3,34; г) свой ответ
-
Найдите координаты середины отрезка AB, если
A(2; 6); B(0; -2)
а) (1; -2); б) (-2; 1); в) (1; 2); г) свой ответ
-
Какова последняя цифра числа:
1 · (2+3) · 4 · (5+6) · 7 · (8+9)?
а) 1; б) 0; в) 5; г) свой ответ
ИТОГОВЫЙ ТЕСТ
Вариант 3
-
Найдите значение выражения:
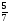
а) 1,7; б) 4,12; в) 2,6; г) свой ответ
-
За 1,4 часа автомобиль прошел 91 км. За какое время автомобиль пройдет 351 км, если будет двигаться с той же средней скоростью?
а) 5,3 ч; б) 5,4 ч; в) 5,5 ч; г) свой ответ
-
Решите уравнение:
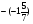
а) 6,4; б) 7,5; в) 8,6; г) свой ответ
-
Какую цифру следует поставить вместо в число 5551, чтобы полученное число делилось на 6?
а) 2; б) 3; в) 4; г) свой ответ
-
Теплоход за три дня прошел 800 км. В первый день он прошел 0,25 пути, а во второй- 43% оставшегося пути. Какое расстояние он прошел за третий день?
а) 244 км; б) 325 км; в) 342 км; г) свой ответ
-
Найдите число, 48% которого равны 1008.
а) 2100; б) 483,84; в) 504; г) свой ответ
-
Упростите выражение: 3· (3-2а)+3 · (3а-6)
а) а-6; б) а+30;
в) 17а-6; г) свой ответ
-
Длина окружности равна 16 см. Найдите ее диаметр. Ответ округлите до сотых.
а) 10,18; б) 2,545; в) 5,09; г) свой ответ
-
Найдите координаты середины отрезка AB, если
A(-1; -4); B(5; -2)
а) (2; -3); б) (-2; -3); в) (2; 3); г) свой ответ
-
Какова последняя цифра числа:
72 · 92 · 112 · 132 · 152· 172 · 192?
а) 1; б) 0; в) 5; г) свой ответ
ИТОГОВЫЙ ТЕСТ
Вариант 4
-
Найдите значение выражения:
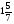
а) 6; б) 7; в) 8; г) свой ответ
-
За 4,6 часа автомобиль прошел 253 км. За какое время автомобиль пройдет 341 км, если будет двигаться с той же средней скоростью?
а) 6,6 ч; б) 6,4 ч; в) 5,5 ч; г) свой ответ
-
Решите уравнение:
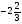
а) 1,3; б) -1,4; в) 1,4; г) свой ответ
-
Какую цифру следует поставить вместо в число 6781, чтобы полученное число делилось на 6?
а) 2; б) 4; в) 6; г) свой ответ
-
Теплоход за три дня прошел 1200 км. В первый день он прошел
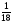 пути, а во второй- 56% оставшегося пути. Какое расстояние он прошел за третий день?
пути, а во второй- 56% оставшегося пути. Какое расстояние он прошел за третий день?
а) 352 км; б) 128 км; в) 400 км; г) свой ответ
-
Найдите число, 56% которого равны 728.
а) 407,68; б) 2000; в) 1300; г) свой ответ
-
Упростите выражение: 6· (а-3,2)-(4,8-а)
а) 7а-24; б) 5а-24;
в) 5а-14,4; г) свой ответ
-
Длина окружности равна 8 см. Найдите ее диаметр. Ответ округлите до сотых.
а) 2,55; б) 5,1; в) 1,275; г) свой ответ
-
Найдите координаты середины отрезка AB, если
A(-6; -5); B(3; 6)
а) (0; 1); б) (2; 1); в) (0; -1); г) свой ответ
-
Какова последняя цифра числа:
112+133+152+172+192?
а) 2; б) 5; в) 3; г) свой ответ
Контрольная работа №1
Вариант I
1.Найдите:
а) наибольший общий делитель чисел 24 и 18
б) наименьшее общее кратное чисел 12 и 15
2. Разложите на простые множители число 546.
3. Какую цифру можно записать вместо звездочки в числе 681*, чтобы оно
а) делилось на 9
б) делилось на 5
в) было кратно 6
4. Выполните действия
а) 7 - 2,35 + 0,435
б) 1,763:0,086 - 0,34∙16
5. Найдите произведение чисел a и b, если их наименьшее общее кратное равно 420, а наибольший общий делитель равен 30.
Контрольная работа №1
Вариант II
1. Найдите
а) наибольший общий делитель чисел 28 и 42
б) наименьшее общее кратное чисел 20 и 35
2. Разложите на простые множители число 510.
3. Какую цифру можно записать вместо звездочки в числе 497*, чтобы оно
а) делилось на 3
б) делилось на 10
в) было кратно 9
4. Выполните действия
а) 9 - 3,46 +0,535
б) 2,867:0,094 + 0,31∙15
5. Найдите наименьшее общее кратное чисел m и n, если их произведение равно 67200, а наибольший общий делитель равен 40.
Контрольная работа №2
Вариант I
1. Сократите: 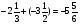
2. Выполните действия
а) 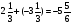 б)
б) 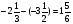 в)
в) 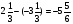
3. Решите уравнение
а) 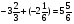 б) 5,86х + 1,4х = 76,23
б) 5,86х + 1,4х = 76,23
4. В первые сутки теплоход прошёл 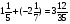 всего пути, во вторые сутки - на
всего пути, во вторые сутки - на 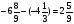 пути больше, чем в первые. Какую часть всего пути теплоход прошел за эти двое суток?
пути больше, чем в первые. Какую часть всего пути теплоход прошел за эти двое суток?
5. Найдите четыре дроби, каждая из которых больше 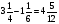 и меньше
и меньше 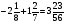 .
.
Контрольная работа №2
Вариант II
1. Сократите: 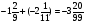
2. Выполните действия
а) 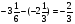 б)
б) 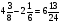 в)
в) 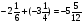
3. Решите уравнение
а) 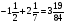 б) 6,28х - 2,8х = 36,54
б) 6,28х - 2,8х = 36,54
4. В первый день засеяли 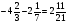 всего поля, во второй день засеяли на
всего поля, во второй день засеяли на 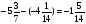 поля меньше, чем в первый. Какую часть поля засеяли за эти два дня?
поля меньше, чем в первый. Какую часть поля засеяли за эти два дня?
5. Найдите четыре дроби, каждая из которых больше 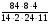 и меньше
и меньше 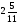 .
.
Контрольная работа №3
Вариант I
1. Сравните числа
а) 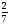 и
и 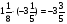 б)
б) 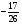 и
и 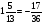 в) 0,48 и
в) 0,48 и 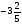
2. Найдите значение выражения
а) 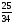 б)
б) 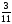 в)
в) 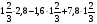 г)
г) 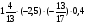
3. На автомашине планировали перевезти сначала 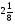 т груза, а потом ещё
т груза, а потом ещё 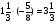 т. Однако перевезли на
т. Однако перевезли на 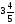 т меньше, чем предполагали. Сколько всего тонн груза перевезли на автомашине?
т меньше, чем предполагали. Сколько всего тонн груза перевезли на автомашине?
4. Решите уравнение
а) 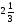 б) 3,45∙(2,08 - к) = 6,21
б) 3,45∙(2,08 - к) = 6,21
5. Представьте дробь 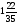 в виде суммы трех дробей, у каждой из которых числитель равен 1.
в виде суммы трех дробей, у каждой из которых числитель равен 1.
Контрольная работа №3
Вариант II
1. Сравните числа
а) 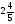 и
и 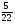 б)
б) 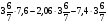 и
и 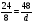 в)
в) 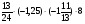 и 0,72
и 0,72
2. Найдите значения выражения
а)7 - 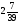 б)
б) 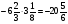 в)
в) 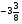 г)
г)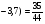
3. С одного опытного участка рассчитывали собрать 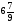 т пшеницы, а с другого
т пшеницы, а с другого 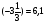 т. Однако с них собрали на
т. Однако с них собрали на 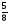 т пшеницы больше. Сколько тонн пшеницы собрали с этих двух участков?
т пшеницы больше. Сколько тонн пшеницы собрали с этих двух участков?
4. Решите уравнение
а) 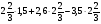 б) 2,65∙(к - 3,06) = 4,24
б) 2,65∙(к - 3,06) = 4,24
5. Представьте дробь 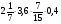 в виде суммы трех дробей, у каждой из которых числитель равен 1.
в виде суммы трех дробей, у каждой из которых числитель равен 1.
Контрольная работа №4
Вариант I
1. Найдите произведение
а) 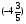 б)
б) 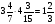 в)
в)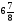 г)
г)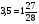 д)
д) 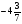
2. Выполните действия
а) 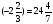 б) (4,2:1,2 - 1,05)∙1,6
б) (4,2:1,2 - 1,05)∙1,6
3. В один пакет насыпали  кг пшена, а в другой
кг пшена, а в другой 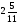 этого количества. На сколько меньше пшена насыпали во второй пакет чем в первый?
этого количества. На сколько меньше пшена насыпали во второй пакет чем в первый?
4. Упростите выражение 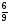 и найдите его значение при к =
и найдите его значение при к = 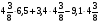 .
.
5. В овощехранилище привезли 320т овощей. 75% привезенных овощей составлял картофель, а 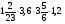 остатка - капуста. Сколько тонн капусты привезли в овощехранилище?
остатка - капуста. Сколько тонн капусты привезли в овощехранилище?
Контрольная работа №4
Вариант II
1. Найдите произведение
а) 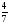 б)
б) 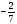 в)
в) 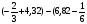 г)
г) 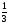 д)
д) 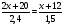
2. Выполните действия
а) 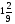 б) (6,3:1,4 - 2,05)∙1,8
б) (6,3:1,4 - 2,05)∙1,8
3. Площадь одного участка земли 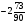 га, а другого - в
га, а другого - в 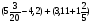 раза больше. На сколько гектаров площадь первого участка меньше площади второго?
раза больше. На сколько гектаров площадь первого участка меньше площади второго?
4. Упростите выражение 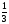 и найдите его значение при к =
и найдите его значение при к =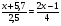 .
.
5. В книге 240 страниц. Повесть занимает 60% книги, а рассказы 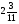 остатка. Сколько страниц в книге занимают рассказы?
остатка. Сколько страниц в книге занимают рассказы?
Контрольная работа №5
Вариант I
1. Выполните действия
а) 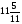 б)
б) 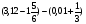 в)
в) 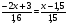 г)
г) 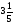 д)
д) 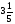
2. За 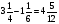 кг конфет заплатили 15р. Сколько стоит 1кг этих конфет?
кг конфет заплатили 15р. Сколько стоит 1кг этих конфет?
3. Решите уравнение
а) 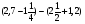 б) (3,1х + х):0,8 = 2,05
б) (3,1х + х):0,8 = 2,05
4. У Сережи и Пети всего 69 марок. У Пети марок в 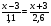 раза больше, чем у Сережи. Сколько марок у каждого из мальчиков?
раза больше, чем у Сережи. Сколько марок у каждого из мальчиков?
5. Сравните числа р и к, если 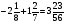 числа р равны 35% числа к.
числа р равны 35% числа к.
Контрольная работа №5
Вариант II
1. Выполните действия
а) 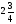 б)
б) 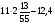 в)
в) 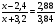 г)
г) 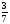 д)
д) 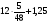
2. За 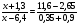 печенья заплатили 6р. Сколько стоит 1кг этого печенья?
печенья заплатили 6р. Сколько стоит 1кг этого печенья?
3. Решите уравнение:
а) 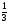 б) (7,1у - у):0,6 = 3,05
б) (7,1у - у):0,6 = 3,05
4. В два железнодорожных вагона погрузили 91 т угля. Во втором вагоне угля оказалось в  раза больше. Сколько угля погрузили в каждый из этих вагонов?
раза больше. Сколько угля погрузили в каждый из этих вагонов?
5. Сравните числа р и к, если 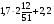 числа р равны 15% числа к.
числа р равны 15% числа к.
Контрольная работа №6
Вариант I
1. Найдите значение выражения:
а) 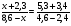 б)
б) 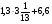 в)
в) 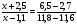
2. Решите уравнение 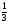
3. Вспахали 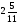 поля, что составило 210 га. Какова площадь всего поля?
поля, что составило 210 га. Какова площадь всего поля?
4. Заасфальтировали 35% дороги, после чего осталось заасфальтировать ещё 13 км. Какова длина всей дороги?
5. 0,9 от 20% числа р равны 5,49. Найдите число р.
Контрольная работа №6
Вариант II
1. Найдите значение выражения:
а) 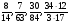 б)
б) 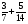 в)
в) 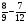
2. Решите уравнение 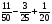
3. Заасфальтировали 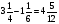 дороги, что составило 45 км. Какова длина всей дороги?
дороги, что составило 45 км. Какова длина всей дороги?
4. Вспахали 45% поля, после чего осталось вспахать ещё 165 га. Какова площадь всего поля?
5. 0,7 от 40% числа d равны 2,94. Найдите число d.
Контрольная работа №7
Вариант I
1. Решите уравнение 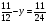
2. Автомобиль первую часть пути прошёл за 2,8 ч, а вторую - за 1,2ч. Во сколько раз меньше времени израсходовано на вторую часть пути, чем на первую? Сколько процентов всего времени движения затрачено на первую часть пути?
3. В 8 кг картофеля содержится 1,4 кг крахмала. Сколько крахмала содержится в 28 кг картофеля?
4. Поезд путь от одной станции до другой прошёл за 3,5 ч со скоростью 70 км/ч. С какой скоростью должен был идти поезд, чтобы пройти этот путь за 4,9ч?
5. 40% от 30% числа х равны 7,8 Найдите число х.
Контрольная работа №7
Вариант II
1. Решите уравнение 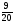
2. Трубу разрезали на две части длиной 3,6м и 4,4м. Во сколько раз первая труба короче второй? Сколько процентов длины всей трубы составляет длина первой её части?
3. Из 6 кг льняного семени получается 2,7 кг масла. Сколько масла получится из 34 кг семян льна?
4. Теплоход прошел расстояние между двумя пристанями со скоростью 40 км/ч за 4,5ч. С какой скоростью должен идти теплоход, чтобы пройти это расстояние за 3,6ч?
5. 60% от 40% числа у равны 8,4. Найдите число у.
Контрольная работа №8
Вариант I
1. Найдите длину окружности, если её диаметр равен 25 см. Число п округлите до десятых.
2. Расстояние между двумя пунктами на карте равно 3,8 см. Определите расстояние между этими пунктами на местности, если масштаб карты 1:100000.
3. Найдите площадь круга, радиус которого равен 6 м. Число п округлите до десятых.
4. Цена товара понизилась с 42,5р. до 37,4р. На сколько процентов понизилась цена товара?
5. Прямоугольный земельный участок изображен на плане в масштабе 1:300. Какова площадь земельного участка, если площадь его изображения на плане 18 см2.
Контрольная работа №8
Вариант II
1. Найдите длину окружности, если её диаметр равен 15 дм. Число п округлите до десятых.
2. Расстояние между двумя пунктами на карте равно 8,2 см. Определите расстояние между этими пунктами на местности, если масштаб карты 1:10000.
3. Найдите площадь круга, радиус которого равен 8 см. Число п округлите до десятых.
4. Цена товара понизилась с 57,5 до 48,3 р. На сколько процентов понизилась цена товара?
5. Прямоугольный земельный участок изображен на плане в масштабе 1:400. Какова площадь земельного участка, если площадь его изображения на плане 16 см2?
Контрольная работа №9
Вариант I
-
Отметьте на координатной прямой точки А(-5), С(3), Е(4,5), К(-3), N(-0,5), S(6).
2. Сравните числа: а) 2,8 и -2,5; б) -4,1 и -4; в) 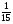
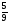 и
и 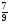 , г) 0 и
, г) 0 и 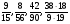
3. Найдите значение выражения:
а) |-6,7| + |-3,2|; б) |2,73|:|-2,1| в) 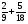
4. Решите уравнение:
а) -х=3,7 б) -у=-12,5 в) |х|=6
5. Сколько целых решений имеет неравенство -18<x<174
Контрольная работа №9
Вариант II
1. Отметьте на координатной прямой точки B(-6), D(-3,5), F(4), M(0,5), P(-4), T(5).
2. Сравните числа: а) -4,6 и 4,1, б) -3 и -3,2, в) 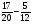 , г)
, г)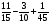
3. Найдите значение выражения:
а) |-5,2| + |3,6|, б) |-4,32|:| - 1,8|, в) 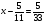
4. Решите уравнение:
а) -у = 2,5 б) -х = -4,8 в) |y| = 8
5. Сколько целых решений имеет неравенство -26<y<158?
Контрольная работа №10
Вариант I
1. Выполните действие:
а) 42-45 г) 17-(-8)
б) -16-31 д) -3,7-2,6
в) -15+18 е) 
2. Найдите расстояние между точками координатной прямой:
а) М(-13) и К(-7) б) В(2,6) и Т(-1,2)
3. Решите уравнение:
а) х - 2,8 = -1,6 б) 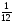
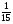
4. Цена товара повысилась с 84р. до 109,2р. На сколько процентов повысилась цена товара?
5. Решите уравнение |x-3|=6
Контрольная работа №10
Вариант II
1. Выполните действие:
а) -39+42 г) -16 - (-10)
б) -17-20 д) 4,3 - 6,2
в) 28-35 е) 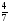
2. Найдите расстояние между точками координатной прямой:
а) N(-4) и С(-9); б) А(-6,2) и Р(0,7)
3. Решите уравнение:
а) 3,2 - х = -5,1 б) 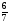
4. Цена товара повысилась с 92р. до 110,4 р. На сколько процентов повысилась цена товара?
5. Решите уравнение |y + 2| = 8
Контрольная работа №11
Вариант I
1. Выполните умножение:
а) -8∙12 в) 0,8∙(-2,6)
б) -14∙(-11) г) 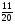
2. Выполните деление:
а) 63:(-21) в) -0,325:1,3
б) -24:(-6) г) 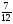
3. Решите уравнение:
а) 1,8у = -3,69 б) х:(-2,3) = -4,6
4. Представьте числа 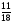 и
и 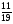 в виде периодических дробей. запишите приближенные значения данных чисел, округлив периодические дроби до сотых.
в виде периодических дробей. запишите приближенные значения данных чисел, округлив периодические дроби до сотых.
5. Сколько целых решений имеет неравенство |x| <64
Контрольная работа №11
Вариант II
1. Выполните умножение:
а) 14∙(-6) в) -0,7∙3,2
б) -12∙(-13) г) 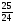
2. Выполните деление:
а) -69:23 в) 0,84:(-2,4)
б) -35:(-7) г) 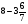
3. Решите уравнение
а) -1,4х =-4,27 б) у:3,1 = -6,2
4. Представьте числа 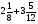 и
и 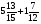 в виде периодических дробей. Запишите приближенные значения данных чисел, округлив периодические дроби до сотых.
в виде периодических дробей. Запишите приближенные значения данных чисел, округлив периодические дроби до сотых.
5. Сколько целых решений имеет неравенство |y|<72?
Контрольная работа №12
Вариант I
1. Найдите значение выражения:
а) раскрыв скобки: 34,4 - (18,1 - 5,6) + (-11,9 +8)
б) применив распределительное свойство умножения:
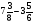
2. Упростите выражение:
а) 4m - 6m - 3m+7+m
б) -8(к-3)+4(к-2)-2(3к+1)
в) 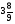
3. Решите уравнение 0,6(у-3) - 0,5(у-1) = 1,5
4. Путешественник 3ч ехал на автобусе и 3ч - на поезде, преодолев за это время путь в 390 км. Найдите скорость автобуса, если она втрое меньше скорости поезда.
5. Найдите корни уравнения (2,5у -4)(6у+1,8) = 0
Контрольная работа №12
Вариант II
1. Найдите значение выражения:
а) раскрыв скобки: 28,3+(-1,8+6) - (18,2-11,7)
б) применив распределительное свойство умножения:
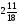
2. Упростите выражение:
а) 6+4а-5а+а-7а
б) 5(р-2)-6(р+3)-3(2р-9)
в) 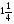
3. Решите уравнение 0,8(х-2)-0,7(х-1) = 2,7
4. Туристы путь в 270 км проделали, двигаясь 6ч на теплоходе и 3ч - на автобусе. Какова была скорость теплохода, если она вдвое меньше скорости автобуса?
5. Найдите корни уравнения (4,9+3,х)(7х-2,8) = 0
Контрольная работа №13
Вариант I
1. Решите уравнение:
а) 8у = -62,4+5у б)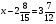
2. В одной бочке в 3 раза больше бензина, чем в другой. Если из первой бочки отлить 78 л бензина, а во вторую добавить 42л, то бензина в бочках будет поровну. сколько бензина в каждой бочке?
3. Найдите корень уравнения 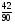
4. Скорость автобуса на 26 км/ч меньше скорости легкового автомобиля. Автобус за 5ч проходит такой же путь, как легковой автомобиль за 3ч. Найдите скорость автобуса.
5. Найдите два корня уравнения |-0,42| = |y|∙|-2,8|
Контрольная работа №13
Вариант II
1. Решите уравнение:
а) 7х = -95,4-2х б) 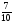
2. В одном зале кинотеатра в 2 раза больше зрителей, чем в другом. Если из первого зала уйдут 37 человек, а во второй придут 50, то зрителей в обоих залах будет поровну. Сколько зрителей в каждом зале?
3. Найдите корень уравнения 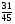
4. Теплоход за 7ч проходит такой же путь, как катер за 4ч. Найдите скорость теплохода, если она меньше скорости катера на 24 км/ч.
5. Найдите два корня уравнения |-0,85| = |-3,4|∙|x|
Контрольная работа №14
Вариант I
1. На координатной плоскости постройте отрезок MN и прямую АК, если М(-4;6), N(-1;0), А(-8;-1), К(6;6). Запишите координаты точек пересечения прямой АК с построенным отрезком и осями координат.
2. Постройте угол ВОС, равный 60о. Отметьте на стороне ОВ точку F и проведите через нее прямые, перпендикулярные сторонам угла ВОС.
3. Постройте угол, равный 105о. Отметьте внутри этого угла точку D и проведите через нее прямые, параллельные сторонам угла.
4. Начертите на координатной плоскости такую фигуру, абсцисса и ордината любой точки которой удовлетворяют условиям: -3≤х≤2, -1≤у≤1.
Контрольная работа №14
Вариант II
1. На координатной плоскости постройте отрезок CD и прямую ВЕ, если С(-3;6), D(-6;0), В(-6;5), Е(8;-2). Запишите координаты точек пересечения прямой ВЕ с построенным отрезком и осями координат.
2. Постройте угол АОК, равный 50о. Отметьте на стороне ОА точку М и проведите через нее прямые, перпендикулярные сторонам угла АОК.
3. Постройте угол, равный 115о. Отметьте внутри этого угла точку N и проведите через нее прямые, параллельные сторонам угла.
4. Начертите на координатной плоскости такую фигуру, абсцисса и ордината любой точки которой удовлетворяют условиям: -1≤х≤4, -2≤у≤2.
6 класс
Итоговая контрольная работа
Вариант I
1. Найдите значение выражения: 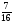
2. Решите уравнение: 1,2х - 0,6 = 0,8х - 27
3. Постройте отрезок АК, где А(2,5), К(-4,-1), и запишите координаты точек пересечения этого отрезка с осями координат.
4. Решите с помощью уравнения задачу. За два дня на элеватор отправили 574 т зерна, причем в первый день в 1,8 раза меньше, чем во второй. Сколько тонн зерна было отправлено в первый день и сколько - во второй?
5. На экзамене 30% шестиклассников получили оценку «5». Сколько учеников в классе, если пятерки получили 9 человек?
6 класс
Итоговая контрольная работа
Вариант II
1. Найдите значение выражения: 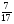
2. Решите уравнение: 1,4х + 14 = 0,6х + 0,4
3. Постройте отрезок ВМ, где В(-1;4), М(5; -2), и запишите координаты точек пересечения этого отрезка с осями координат.
4. Решите с помощью уравнения задачу. В школе 671 ученик, причем девочек в 1,2 раза больше, чем мальчиков. Сколько девочек и сколько мальчиков учатся в школе?
5. Тракторист вспахал 70% поля. Какова площадь поля, если вспахано 56 га?
Раздел V. Требования к уровню подготовки учащихся за курс математики 6 класса.
В результате изучения математики ученик должен
знать/понимать
-
существо понятия алгоритма; приводить примеры алгоритмов;
-
как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
-
как математический язык может описывать реальные зависимости; приводить примеры такого описания;
-
как потребности практики привели математическую науку к необходимости расширения понятия числа;
-
каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждений о них, важных для практики;
Арифметика
уметь
-
выполнять устно арифметические действия: сложение и вычитание двузначных чисел и десятичных дробей с двумя знаками, умножение однозначных чисел, арифметические операции с обыкновенными дробями с однозначным знаменателем и числителем;
-
переходить от одной формы записи чисел к другой, представлять десятичную дробь в виде обыкновенной и в простейших случаях обыкновенную в виде десятичной, проценты - в виде дроби и дробь - в виде процентов
-
выполнять арифметические действия с рациональными числами, сравнивать рациональные числа; находить значения числовых выражений;
-
округлять целые числа и десятичные дроби, находить приближения чисел с недостатком и с избытком, выполнять оценку числовых выражений;
-
пользоваться основными единицами длины, массы, времени, скорости, площади, объема; выражать более крупные единицы через более мелкие и наоборот;
-
решать текстовые задачи, включая задачи, связанные с отношением и с пропорциональностью величин, дробями и процентами;
-
решать линейные уравнения.
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
-
решения несложных практических расчетных задач, в том числе c использованием при необходимости справочных материалов, калькулятора, компьютера;
-
устной прикидки и оценки результата вычислений; проверки результата вычисления, с использованием различных приемов.
Алгебра
уметь
-
составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, выражать из формул одну переменную через остальные;
-
решать линейные уравнения;
-
изображать числа точками на координатной прямой;
-
определять координаты точки плоскости, строить точки с заданными координатами;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
-
выполнения расчетов по формулам, для составления формул, выражающих зависимости между реальными величинами; для нахождения нужной формулы в справочных материалах;
Геометрия
уметь
-
распознавать изученные геометрические фигуры, различать их взаимное расположение;
-
изображать изученные геометрические фигуры;
-
распознавать на чертежах, моделях и в окружающей обстановке основные пространственные тела;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
-
построений геометрическими инструментами (линейка, угольник, циркуль, транспортир).
Элементы логики, комбинаторики, статистики и теории вероятностей
уметь
-
извлекать информацию, представленную в таблицах, на диаграммах, графиках; составлять таблицы, строить диаграммы;
-
решать комбинаторные задачи путем систематического перебора возможных вариантов и с использованием правила умножения;
-
вычислять средние значения результатов измерений;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
-
распознавания логически некорректных рассуждений;
-
анализа реальных числовых данных, представленных в виде диаграмм, графиков, таблиц;
-
решения практических задач в повседневной и профессиональной деятельности с использованием действий с числами, процентов, длин, площадей, объемов, времени, скорости;
-
решения учебных и практических задач, требующих систематического перебора вариантов.
Раздел V. УМК
-
Программа. Планирование учебного материала. Математика. 5-6 классы/авт.-сост. В.И. Жохов. - М.:Мнемозина,2010.
-
Учебник: «Математика 6 класс» Н.Я.Виленкин, В.И.Жохов, А.С Чесноков, С.И.Шварцбурд, изд. М.: Мнемозина,2011г
Литература для учителя
-
Жохов В.И., Преподавание математики в 5 и 6 классах.-М.Мнемозина, 2004-2007.
-
Чесноков А.С., Нешков К.И. Дидактические материалы по математике для 5 класса.-М.Просвещение, 1990-2000.
-
Шарыгин И.Ф., Шевкин К.И. Математика. Задачи на смекалку. Учебное пособие для 5-6 классов общеобразовательных учреждений. - М.Просвещение, 1995-1996.
-
Кривоногов В.В. Нестандартные задания по математике: 5-11 классы.-М.Издательство «Первое сентября» 2003.
-
Абдрашитов Б.М. Учитесь мыслить нестандартно»: книга для учащихся.М.Просвещение: АО «Учебная литература» 1996.
-
Попов М.А. Контрольные и самостоятельные работы по математике:6 класс: к учебнику Н.Я. Виленкина и др.:М. «Экзамен»,2013
Литература для учащихся
-
Чесноков А.С., Нешков К.И. Дидактические материалы по математике для 6 класса.-М.Просвещение, 1990-2000.
-
Шарыгин И.Ф., Шевкин К.И. Математика. Задачи на смекалку. Учебное пособие для 5-6 классов общеобразовательных учреждений. - М.Просвещение, 1995-1996.
-
Кривоногов В.В. Нестандартные задания по математике: 5-11 классы.-М.Издательство «Первое сентября» 2003.
-
Абдрашитов Б.М. Учитесь мыслить нестандартно»: книга для учащихся.М.Просвещение: АО «Учебная литература» 1996.
-
Вычисляем без ошибок. Работы с самопроверкой для учащихся 5-6 классов/ С.С. Минаева-М.:Издательство «Экзамен»
-
Н.Я.Виленкин и др. «Математика 5 класс» Учебник для общеобразовательных учреждений. - Москва: Мнемозина, 2008;