Выступление на XII Научно-практической конференции ПЕРВЫЕ ШАГИ В НАУКУ

ХII республиканская научно-практическая конференция школьников

«Первые шаги в науку»

Направление: Математика

Название работы: Теорема Менелая.

Автор работы: Ким Елена Сергеевна

Место выполнения работы: г.Элиста,

Муниципальное бюджетное образовательное

учреждение «Средняя общеобразовательная

школа № 20»

Руководитель: Дочиева И.А.,учитель математики

2016 год

Содержание.

стр.

Введение. Теорема Менелая. Исторический аспект.

§1. История теоремы. 1

1. §2.Теорема Менелая. 2

2. §3. Прямая теорема. 6

3. §4. Обратная теорема. 7

4. §5. Теорема Менелая в декартовой системе координат. 14

5. §6. Теорема Менелая в пространстве. 19

Заключение. 22

Список литературы.

Введение. Теорема Менелая. Исторический аспект.

§1. История теоремы

Рассмотрим теорему, которую доказал Менелай Александрийский. В нашей работе рассматривается теорема Менелая. Менелай Александрийский (I-II в) - знаменитый древнегреческий математик и астроном. Жил в Риме. Известны его работы по сферической тригонометрии. Менелай впервые излагает тригонометрию обособленно от геометрии и астрономии. Сохранились 6 его книг о вычислении хорд и 3 книги «Сферики» (в арабском переводе). В первой книге «Сферики» даны определения и характеристика основных свойств сферического треугольника. В третий книге изложена теорема, позже названная теоремой Менелая: «Если на сторонах ВС, СА, АВ треугольника ABC взяты три точки а, в, с, которые удовлетворяют соотношению:

то эти три точки лежат на одной прямой».

Раньше эта теорема была доказана для больших окружностей на сфере. Теорема Менелая была доказана ученым для сферического треугольника и, по всей вероятности была известна Евклиду (III до н.э.) Менелая теорема является более частным случаем более общей теоремы Карно.

Менелай доказал очень важную роль для геометрии теорему об условии принадлежности трех точек одной прямой

Это соотношение посредством проектирования из центра Менелай переводит на сферу и получает соответствующие соотношения для хорд,

3

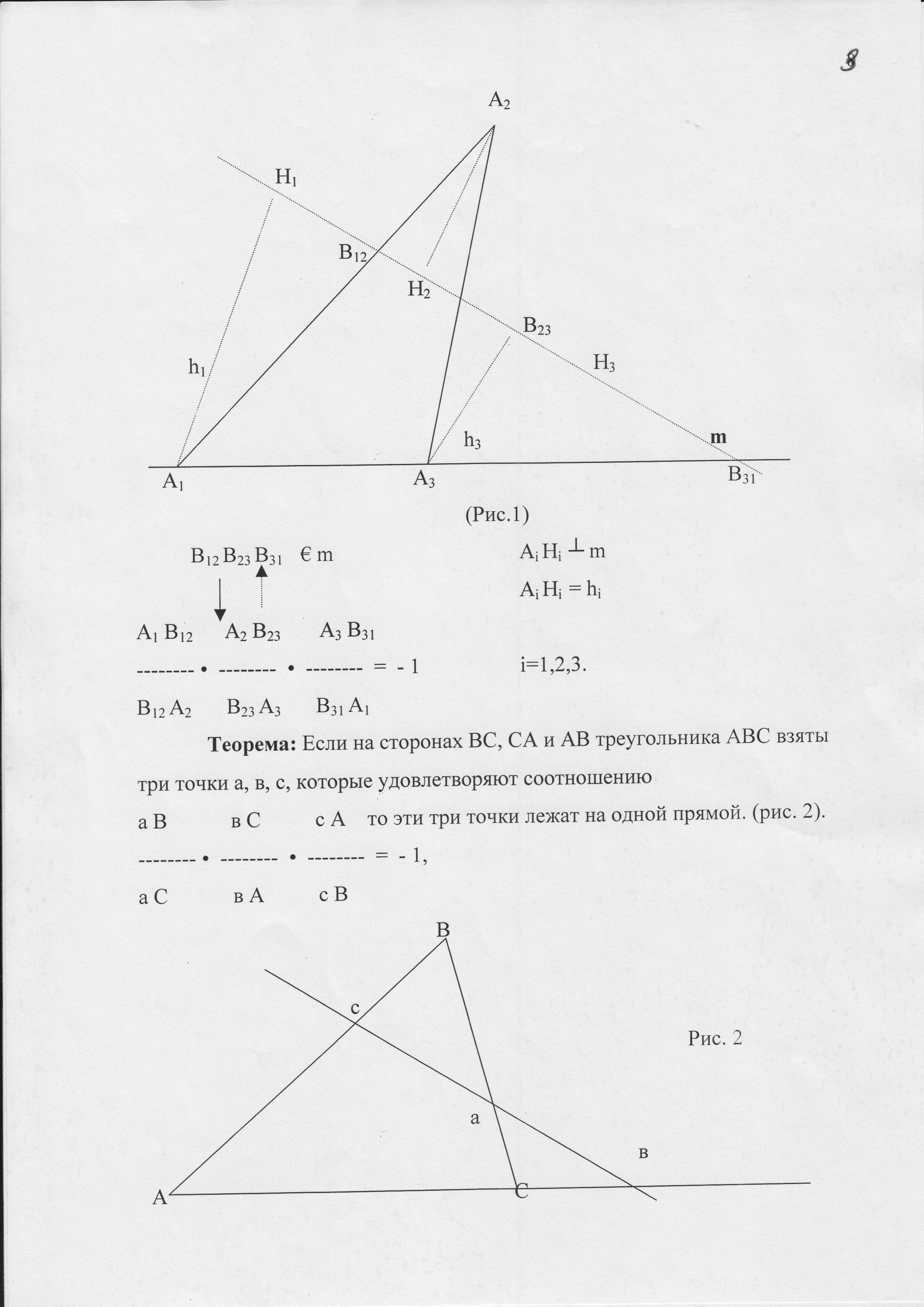
4

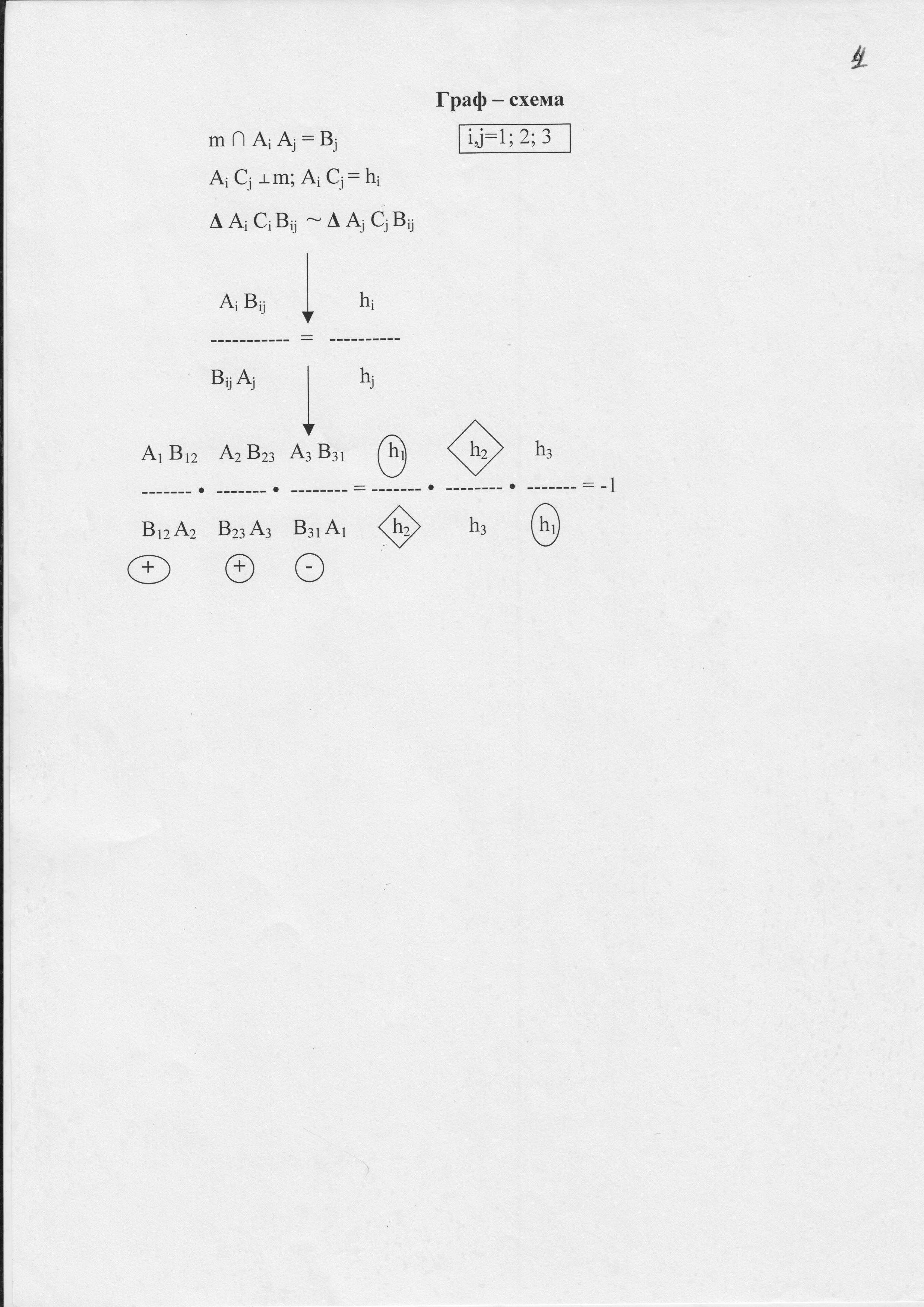
5

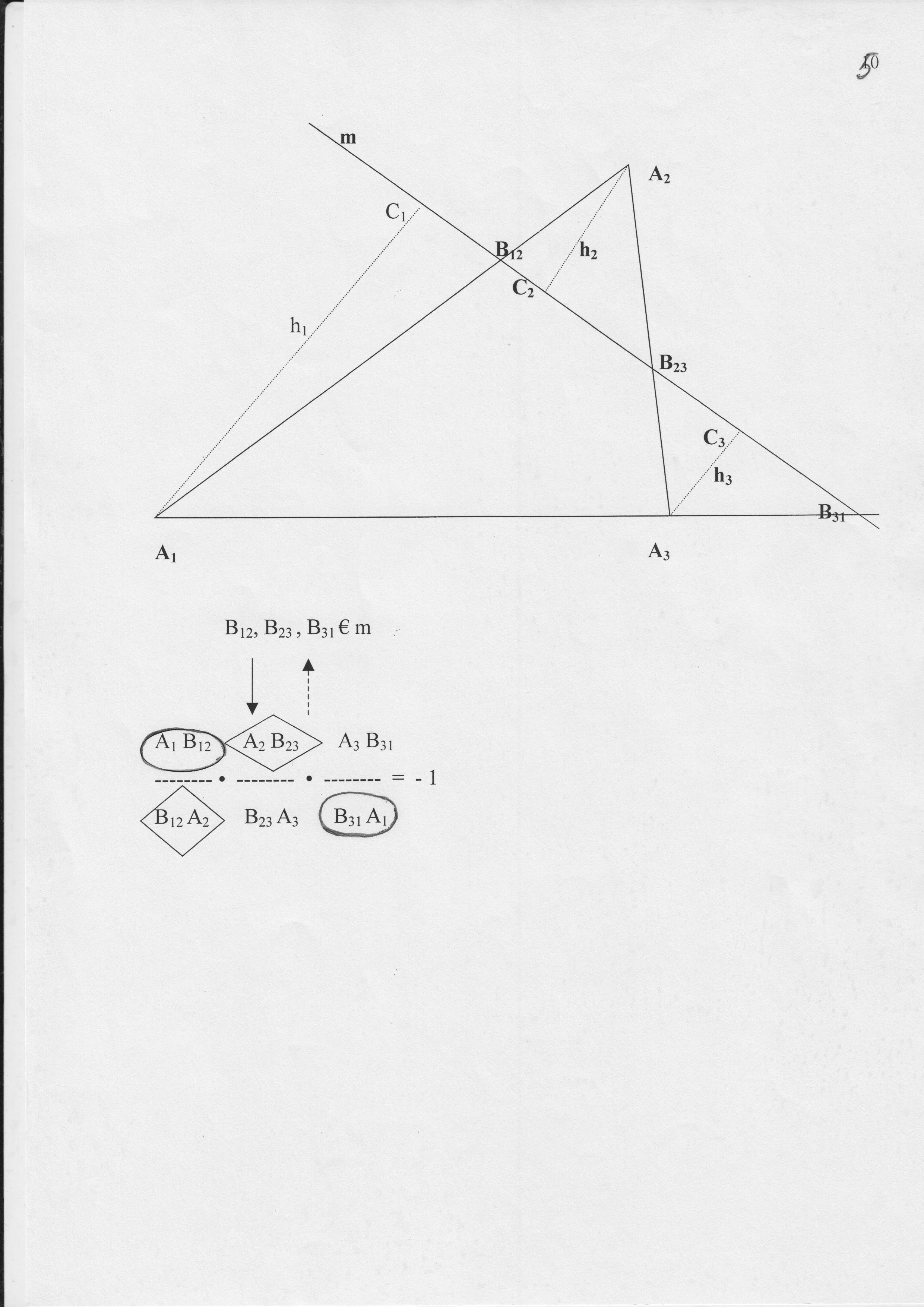
§ 3. Прямая теорема

7

§ 4. Обратная теорема

8

9

10

§ 5. Теорема Менелая в декартовой системе координат

15

16

17

18

19

§ 6. Теорема Менелая в пространстве.

20

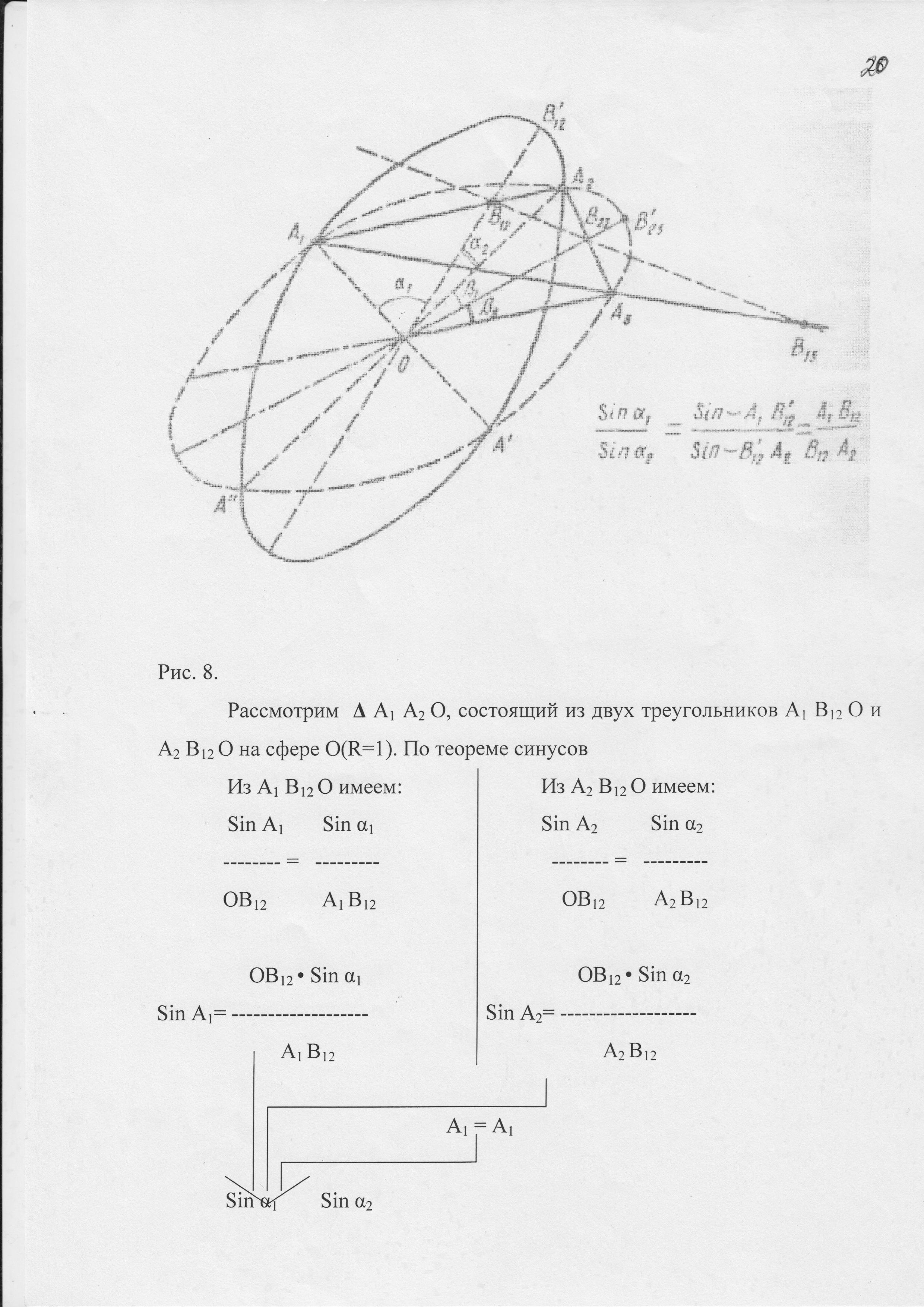
21

22