Разработка урока математики 8 класс Применение свойств квадратного корня

Не пытайтесь объяснить ребёнку то,

до чего он может додуматься сам.

Давайте возможность каждому ребёнку

сделать своё маленькое открытие

Э.И. Александрова.

ОТКРЫТЫЙ УРОК

Тема урока: Применение свойств арифметического квадратного корня.

Цель урока:

• Получение способа вынесения множителя из-под знака корня.

• Получение способа внесения множителя под знак корня.

• Развитие навыка извлечения квадратного корня из числа.

• Развитие логического мышления, умения анализировать, делать выводы.

• Развитие умения прислушиваться к чужому мнению, навыка самооценки и взаимооценки

Тип урока: Открытие новых знаний

Результат урока:

• Способы внесения под знак корня и вынесения из-под знака корня, представленные в виде знаковых моделей.

• Первичный контроль над применением полученных способов.

Этапы урока:

1. Организационный момент. Запись домашнего задания (п.17 № 403, № 411).

2. Тренажёр (набор отработочных заданий по теме «Арифметический квадратный корень»)

Время проведения: 3 минуты. Критерии оценки (по количеству правильных ответов):Для оперативной проверки результатов выполнения тренажёров каждому ученику выдаётся индивидуальный лист ответов, а после проведения работы - лист правильных ответов. Тексты тренажёра и листов ответов прилагаются (см. приложение 1).

Проверку результатов осуществляют сами учащиеся, работая в парах. Оценивают друг друга, руководствуясь критерием.

3. Устные упражнения.

Выполните устно:

Сравните выражения

:

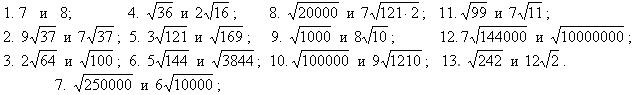
В заданиях 8-13 "спрятана проблема"- корни из предложенных чисел не извлекаются. Поняв, что обычный способ сравнения выражений не подходит, учащиеся начинают искать новые пути решения. Это удаётся не сразу. Задания 8 -13 выполняют не по порядку, а выбирают то, решение которого наметили. Для 8А таким ключевым стало задание № 11.

Эля Борисенко предлагает "разбить" число 99 на множители 9 и 11 и, используя свойства арифметического квадратного корня, извлечь корень только из числа 9, а 11 оставить под знаком корня. Учащиеся примеряют предложенный Элей вариант решения на остальные задания.

Анализируем свою работу, отвечая на вопросы:

а) Почему не смогли сразу сделать задания 8-13?

б) Чем задания 8-13 отличаются от предыдущих?

в) Почему смогли выполнить задания 8-13?

4. Составление схемы - модели способа.

Задание №1: Придумайте подобные задания (варианты ответов на доске (3, 4) - обсуждение).

Задание №2: Составьте схему полученного способа.

обучающиеся предлагают такой вариант: = а

Эта схема берётся за основную. Учащимся сообщается, что такая операция над числами в алгебре носит название "вынесение множителя из-под знака корня".

5. Выполнение задания № 401 по учебнику "Алгебра-8".

Задания выполняются по цепочке, начиная с третьего ряда (одно выражение - один ученик), с комментированием. Перед началом работы с учащимися обсуждаем, для чего выполнять этот номер. Лена Макарова формулирует цель выполнения: "Для того, чтобы проверить, как работает новый способ, нужно чтобы каждый научился его применять".

6. Выполнение задания № 404 по учебнику "Алгебра-8".

Предлагаю учащимся прочитать задание номера и ответить на вопрос: "Чем это задание отличается от предыдущего?". Учащиеся сразу видят изменение ситуации и поясняют: "В задании № 401 предлагалось вынести множитель из-под знака корня, а в задании № 404 предлагается внести множитель под знак корня. Я думаю, что это "обратный ход". Класс с согласен с данным утверждением. Выполняем по цепочке, начиная со второго ряда.

Обучающий тест. У всех один вариант. Время выполнения 17 минут.

Текст теста, ключи - ответы к нему, критерии оценки прилагаются (см. приложение 2).

8. Дополнительное задание.

Для тех, кто на выполнение теста затрачивает меньше времени, предлагается дополнительная карточка из десяти занимательных заданий. Текст прилагается (см. приложение 3).

9. Подведение итогов урока.

Отвечаем на вопросы:

1) Какие способы работы с арифметическим квадратным корнем получили?

2) Как по-другому можно сформулировать тему сегодняшнего урока?

3) На основании каких свойств можно выполнять внесение множителя под знак корня, вынесение множителя из-под знака корня?

Находки урока (понятийные термины):

- "безквадратное число",

- "вернуть обратно",

- "разбить на множители"

cП р и л о ж е н и е 1.

Тренажёр по теме "Арифметический квадратный корень".

Б

В

Г

Д

Е

1

2

3

-

-

4

-

-

-

-

-

5

6

7

Х² = 4

Х² = 100

Х² = 16

Х² = 30

∙

∙

8

9

П р и л о ж е н и е 2

а) Тест по теме "Применение свойств арифметического квадратного корня"

Тест: Применение свойств арифметического квадратного корня Алгебра - 8

Уровень А

В заданиях 1 - 5

вынесите множитель из-под знака корня

В заданиях 6 - 10

внесите множитель под знака корня

1. А. ; В. ; С. .

2. А.; В. ; С..

3. А.; В.; С. .

4. А.; В.; С..

5. А. - 4; В.; С..

6. А.; В.; С..

7. А.; В.; С..

8. А.; В.; С. .

9. А.; В.; С..

10. А.; В.; С..

Ключ:

</ Уровень В

Преобразуйте выражение: Ключ:

11) ; 12) ; 13) .

Уровень С

Извлеките корень: Ключ:

14) ; 15) .

б) Критерии оценки

Уровень

Количество баллов за правильный ответ

Максимальное количество баллов за уровень

А

1 балл

10 баллов

В

2 балла

6 баллов

С

3 балла

6 баллов

П р и л о ж е н и е 3

а) Дополнительное задание.

Карточка № 5 Алгебра - 8

1. Найдите значение корня:

1.;

2. ;

3. ;

4. ;

5. ;

6. ;

7. ;

8. ;

9. ;

10. ;

2. Придумайте три подобных задания.