Разработка урока по математике в 5 классе по теме Буквенная запись свойств сложения и вычитания

Открытый урок в 5 классе по теме:

«Буквенная запись свойств сложения и вычитания»

Учебник «Математика 5 класс», Н.Я. Виленкин, В.И.Жохов и др

учитель математики и информатики Костанян А.С.

Весь представленный в работе материал соответствует реальному ходу урока.

Тип урока: урок обобщения и систематизации знаний.

Цели урока:

Образовательная: повторить буквенную запись свойств сложения и вычитания, совершенствовать вычислительные навыки.

Развивающая: развитие речи, мышления, внимания

Воспитательная: проявление познавательного интереса к изучению математики (применение интерактивной доски, игровые моменты) воспитание научного мировоззрения, формирование учебно-коммуникативных и учебно-интеллектуальных умений.

Оборудование: интерактивная Smart-доска, компьютер, проектор, карточки с заданиями

Методы: беседа, эвристический метод.

Структура урока:

1. Организационный момент

2. Актуализация опорных знаний и умений

3. Работа с материалом по текущей теме

4. Физминутка

5. Самостоятельная работа

6. Закрепление изученного материала

7. Постановка домашнего задания

8. Подведение итогов урока

Ход урока

I. Организационный момент

II. Актуализация опорных знаний и умений

- проверка заданий из домашней работы (сканируется одна из лучших работ учащихся и проверка осуществляется демонстрацией работы), работа над ошибками, демонстрация решения заданий, вызвавших затруднения.

фронтальный теоретический опрос ответить на следующие вопросы

- Знаки, каких действий вы видите на доске (Презентация слайд№2)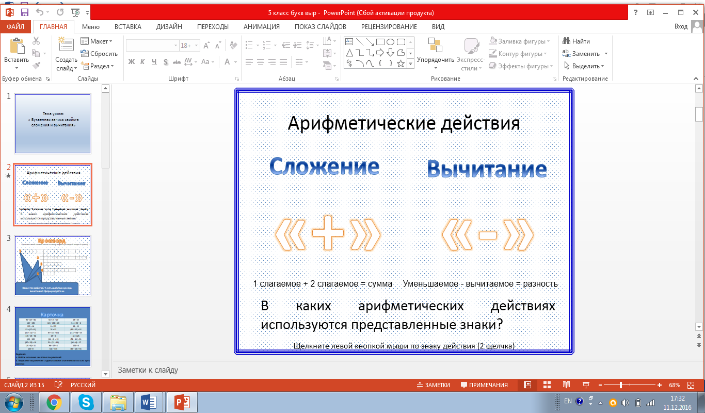

- Вспомним компоненты этих действий.

- Вспомним их свойства.

С целью повторения пройденного материала: разгадывание математического кроссворда и ответты на дополнительные вопросы: слайд №3 (ответы записываются на кроссворде карандашом на доске)

Свойство сложения: от перестановки слагаемых сумма не меняется. (Приведите пример)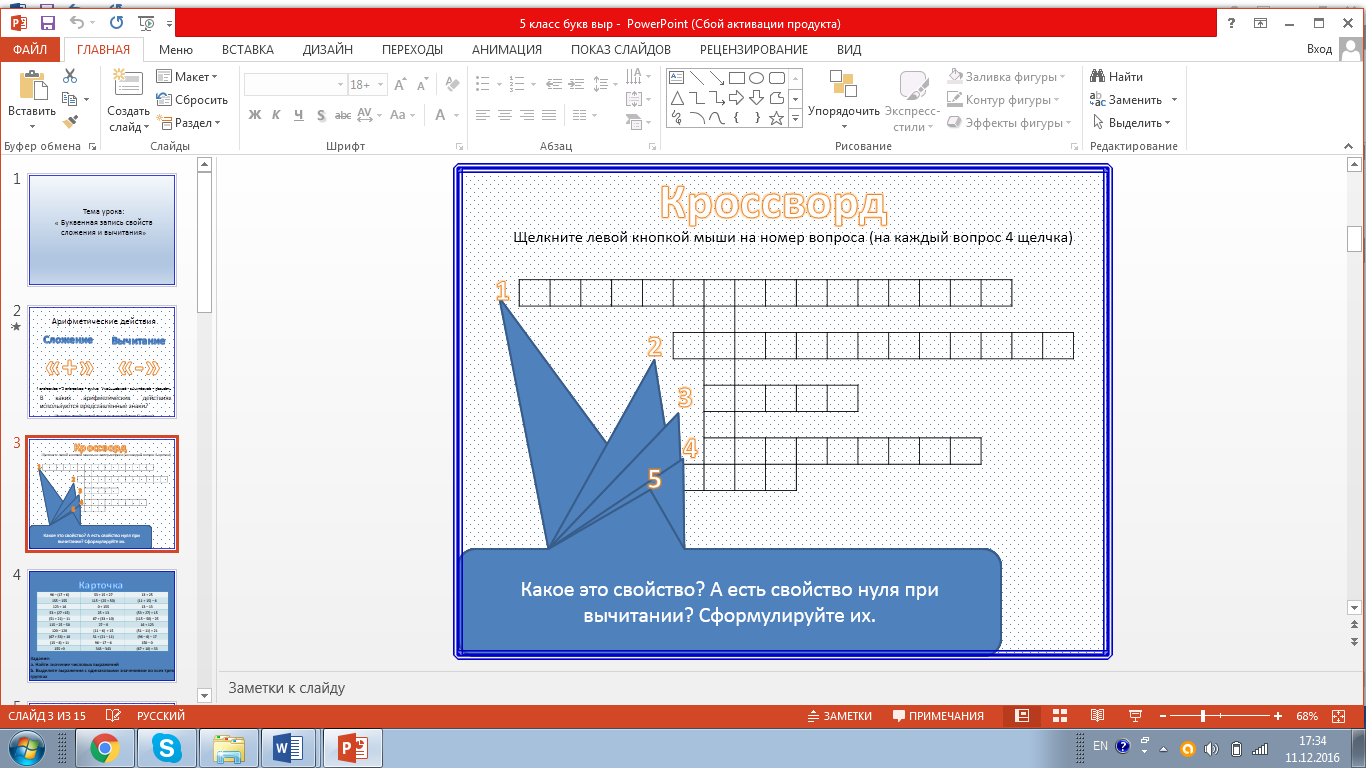

1. Свойство сложения: чтобы прибавить к числу сумму двух чисел, можно сначала прибавить первое слагаемое, а потом к полученной сумме прибавить второе слагаемое. (Приведите пример)

2. "Свойство вычитания числа из …". Какое слово пропущено? (Сформулируйте свойство и приведите пример)

3. "Свойство … суммы из числа". Какое слово пропущено? (Сформулируйте свойство приведите примера)

4. Какое число, сколько не прибавляй его к другому числу, сумма никогда не измениться и будет всегда одной и той же? (Какое это свойство? А есть свойство нуля при вычитании? Сформулируйте свойство)

- Какое ключевое слово у вас получилось? (Свойство)

- А зачем нужно знать свойства сложения и вычитания?

- Как вы думаете, чем мы будем сегодня заниматься на уроке? (Упрощать, применяя свойства при вычислениях)

- Почти угадали, применять мы их обязательно будем, но для начала выведем общую запись для каждого свойства.

III. Ознакомление с новым материалом.

Для начала поработаем в парах и выявим проблему, если таковая есть.

Работа в парах слайд №4(11 + 15) - 6

123 + 16

0 + 155

13 - 13

53+(27+15)

25 + 13

(53 + 27) + 15

(51+21) -11

67 + (33 +10)

(115 - 50) - 25

115 - 25 - 50

27 - 0

16 + 123

(67 + 33) + 10

51 + (21 - 11)

(96 - 6) - 17

155 +0

343 - 343

(67 + 10) + 33

Учащимся раздаются карточки с заданиями, и предлагается выполнить их в паре.

Задание: a. Найти значение числовых выражений

b. Выделите выражения с одинаковыми значениями во всех трех группах

После чего обмен карточками взаимопроверка.

2. Фронтальная работа

- Что интересное вы заметили?

- Чем можно заменить числа в этих равенствах?

Возникает проблема: Чем заменить числа в выражениях, чтобы записать свойства на математическом языке.

3. Поиск решения проблемы.

- Какие два вида математических выражений вы знаете? (числовые и буквенные)

- У вас на карточках, какие выражения? (числовые)

- Чем числовые выражения отличаются от буквенных? слайд №5

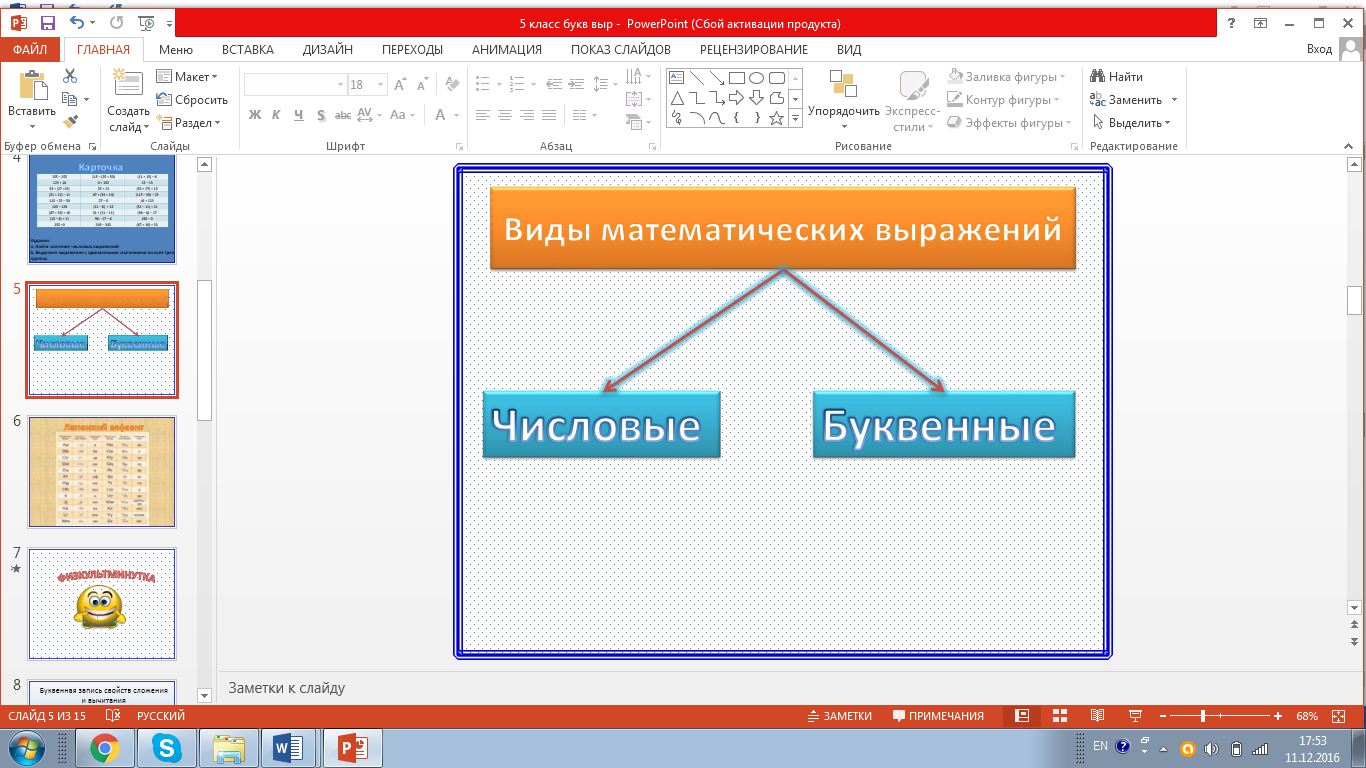
- Какое решение нашей проблемы Вы можете предложить? замена чисел буквами?

- Буквы, какого алфавита мы будем использовать? (Латинского)

- Рассмотрим алфавит, представленный на слайде.№6, который находится также у вас на форзаце учебника

IV. Физкультминутка слайд № 7

- Мы поработали устали, так что надо отдохнуть

- Только будьте внимательны. Начнем! Все встали.

- Руки кверху поднимаем,

А потом их отпускаем.

А потом их развернем

И к себе скорей прижмем.

А потом быстрей, быстрей

Хлопай, хлопай веселей.

- Молодцы!

- И мы с новыми силами можем вернуться к работе. Упр для глаз(при наличии времени)

V.

4. Решение проблемы и изучение полученных результатов.

- Попробуем вместе реализовать упрощение выражений.

- Рассмотрим таблицу, которая представлена на доске и будем ее заполнять.

- Так как мы числа заменили буквами, то такую запись мы будем называть буквенной записью

На слайде представленная незаполненная таблица, которая по мере работы будет заполняться.

Учащиеся подробно разбирают и обсуждают каждое свойство, при этом останавливаясь на значениях букв, какие они могут принимать. с помощью учителя:

1. Переместительное свойство сложения: (пример из карточки)

a + b = b + a

- Какие значения могут принимать буквы а и b? (a, b - любые натуральные числа или 0)

2. Сочетательное свойство сложения:

a + (b + c)= (a + b) + c = a + b + c

- Какие значения могут принимать буквы а, b и с? (a, b и с - любые натуральные числа или 0)

3. Свойство нуля при сложении:

a + 0 = 0 + a = a

- Какие значения может принимать а? (a - любое число)

4. Свойство вычитания числа из суммы:

a - (b + c) = a - b - с

- Какие значения могут принимать буквы а, b и с?

- Например, если a=34, b=23, с=35, мы сможем применить данное свойство?

- Тогда какое ограничение мы должны ввести на а, b и с? Почему?

a - (b + c) = a - b - с, если b + с ? a

- Потому что уменьшаемое не может быть меньше вычитаемого!

5. Свойство вычитания числа из суммы:
   
   (a + b) - с = a + (b - c)=(a - c) + b
   
   - a, b, с могут принимать любые значения?
   
   - Приведите пример, когда мы не можем применить данное свойство?
   
   - Например: a=1, b=5, c=2 или a=13, b=16, c=14
   
   - Какое ограничение тогда напишем? Почему?
   
   (a + b) - с = a + (b - c), если с ? b
   
   (a + b) - с = (a - c) + b, если с ? a
   
   - Потому что уменьшаемое не может быть меньше вычитаемого!

6. Свойство нуля при вычитании:
   
   a - 0 = a, a - a =0
   
   - Какие значения может принимать а? (a - любое натуральное число или нуль)

VI. Закрепление материала., слайды8-12

№ 347, № 348, №339

Учащиеся выполняют данные задания в парах, а один человек работает у доски. После чего выполняется проверка, в том числе и с эталоном, который представлен на слайде, если щелкнуть по номеру задания.

№348

еще раз акцентировать на словах "упростить", и понятии значение выражения

№348

К задаче записать краткую запись

Составить выражение

Упростить данное выражение

Найти значение буквенного выражения

Решение комбинаторной задачи-живая демонстрация задачи с помощью учащихся, подбор вариантов, слайд №7, запись результатов в тетрадь. слайд №13

VII. Постановка домашнего задания слайд № 14

П. 9, №366, 371 (а)

VIII. Подведение итогов урока слайд № 15

- Что нового вы узнали на уроке?

-Повторим еще раз тему урока "Буквенная запись свойств сложения и вычитания"

- Какие были цели нашего урока?

- Как, по-вашему, мы достигли целей?

Используемая литература:

1.Математика 5 класс: учеб. для общеобразоват. учреждений/Н.Я. Виленкин- 35 изд., - М.:Мнемозина, 2016.

2. Дидактические материалы по математике. 5 класс. К учебнику Н.Я. Виленкина "Математика. 5 класс". ФГОС, 2017 г.

</

Организация учебной деятельности в средних классах должна обеспечить ее направленность на формирование теоретического дискурсивного мышления, мышления, основанного на оперировании не конкретными образами и представлениями, а понятиями. Подросток должен научиться сопоставлять эти понятия, переходить в ходе рассуждения от одного суждения к другому и от понятий переходить к реалиям жизни. Поэтому в обучении математике приоритетное значение имеет поисковая деятельность учащихся. Развивающий потенциал поисковой деятельности, который состоит в интеллектуально-нравственном развитии личности, приобретении опыта творческой деятельности, формировании потребности в знаниях и др.

Ученику не интересно получать готовые знания, гораздо интересней их открывать, и чувствовать себя первооткрывателем. И мы учителя можем ему в этом помочь, если правильно организуем урок по изучению новой темы. Данный урок ориентирован на формирование поисковой деятельности, мы можем проследить каждый ее этап: создание проблемной ситуации и формулирование проблемы, поиск способов ее решения, выдвижение гипотез, решение проблемы, изучение полученных результатов и, конечно, обобщение. Учащиеся выступают в роли маленьких исследователей, а учитель в роли их консультанта, который направляет их. При этом он использует игровые и занимательные задания по данному вопросу, которые повышают их познавательную активность.