Конспект урока по теме:Тригонометрия в окружающем нас мире и в жизни человека (10 класс)

Автор: Ямангулова Альбина Маулитовна

Важнейшая задача цивилизации -

научить человека мыслить

Томас Эдисон

Тема урока: Тригонометрия в окружающем нас мире и в жизни человека.

Цели урока:

• Изучить историю возникновения тригонометрии и понять, как зарождались математические понятия, связанные с ней

• Узнать, в каких сферах науки и искусства применяется тригонометрия

• научиться использовать знания, полученные на уроках алгебры, в задачах с практическим содержанием

• создать условия для поддержания интереса к математике через использование обобщающих приёмов умственной деятельности;

• формирование умения мыслить по аналогии;

• способствовать самостоятельной деятельности учащихся;

• развивать логическое мышление.

• научиться решать тригонометрические задачи с целью лучшей подготовки к ЕГЭ

Ход урока.

I. Организационный момент. Сообщение темы и целей урока.

Эпиграфом к нашему уроку являются слова Томаса Эдисона

II. Актуализация опорных знаний. Устная работа.

• Какие тригонометрические функции мы изучаем?

• 1. Разгадываем ребусы.

Синус Тангенс Косинус

III. Изучение нового материала.

История тригонометрии

Что такое тригонометрия ? Слово тригонометрия составилось из двух греческих слов: τρίγονον ( тригонон-треугольник) и и μετρειν ( метрейн - измерять ) в буквальном переводе означает измерение треугольников.

Именно эта задача - измерение треугольников или, как принято теперь говорить, решение треугольников, т. е. определение всех сторон и углов треугольника по трем его известным элементам ( стороне и двум углам, двум сторонам и углу или трем сторонам)- с древнейших времен составляла основу практических приложений тригонометрии.

Как и всякая другая наука, тригонометрия выросла из человеческой практики, в процессе решения конкретных практических задач. Первые этапы развития тригонометрии тесно связаны с развитием астрономии. . Древние люди наблюдали за движением небесных светил. Ученые обрабатывали данные измерений, чтобы вести календарь и правильно определять время начала сева и сбора урожая, даты религиозных праздников. Большое влияние на развитие астрономии и тесно связанной с ней тригонометрии оказали потребности развивающегося мореплавания, для которого требовалось умение правильно определять курс корабля в открытом море по положению небесных светил. Значительную роль в развитии тригонометрии сыграла потребность в составлении географических карт и тесно связанная с этим необходимость правильного определения больших расстояний на земной поверхности.

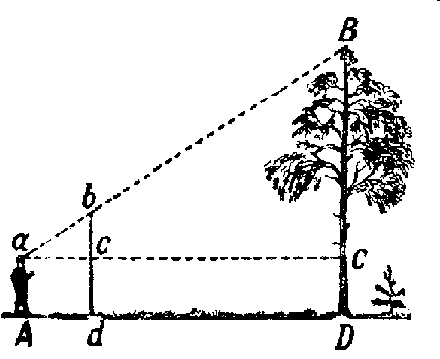
И на Земле не всегда удавалось непосредственно определить расстояние между какими-то пунктами. И тогда вновь прибегали к косвенным измерениям. Например, вычисляли высоту дерева, сравнивая длину его тени с длиной тени от какого-нибудь шеста, высота которого была известна. Подобные задачи сводятся к анализу треугольника, в котором одни его элементы выражают через другие.

Значимые люди в тригонометрии:

Основополагающее значение для развития тригонометрии в эпоху ее зарождения имели работы древнегреческого астронома Гиппарха (середина II века до н. э.) Впрочем, оригинальные таблицы Гиппарха( как и почти все им написанное) до нас не дошли, и мы можем составить себе о них представление главным образом по сочинению « Великое построение» или ( в арабском переводе) « Альмагест» знаменитого астронома Клавдия Птолемея, жившего в середине II века н. э. «Альмагест» содержит таблицу хорд через полградуса от 0° до 180°, которая с нашей современной точки зрения представляет таблицу синусов для углов от 0° до 90° через каждые четверть градуса.

Практическая работа.

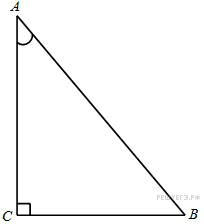
За­да­ние1: В тре­уголь­ни­ке угол равен 90°, . Най­ди­те .

По­яс­не­ние.

Ответ: 0,96.

VII. Итог урока.

Оценивание:

- За работу у доски

- За активное участие на уроке

Рефлексия:

Выразите свое отношение к уроку. Какие новые знание вы получили?

Спасибо за хорошую работу на уроке. До свидания.

VIII. Домашнее задание.

За­да­ние № 2. В тре­уголь­ни­ке угол равен 90°, Най­ди­те

По­яс­не­ние.

Имеем:

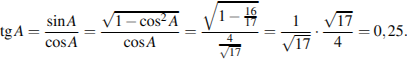
Ответ: 0,25.

</