Муниципальное бюджетное общеобразовательное учреждение

«Гимназия №1»

Тема

«Решение логических задач»

учитель ВВК: Винокурова Т.М.

Воронеж - 2015

Содержание

Предмет математики настолько серьезен, что нельзя упускать случая сделать его немного занимательным.

Блез Паскаль

Введение

Решать логические задачи очень увлекательно. В них вроде бы нет никакой математики - нет ни чисел, ни функций, ни треугольников, ни векторов, а есть только лжецы и мудрецы, истина и ложь. В то же время дух математики в них чувствуется ярче всего - половина решения любой математической задачи (а иногда и гораздо больше половины) состоит в том, чтобы как следует разобраться в условии, распутать все связи между участвующими объектами.

Существуют разные способы решения логических задач. Таких приемов несколько, они разнообразны и каждый из них имеет свою область применения.

Предмет математической логики и его основоположники

Слово "логика" греческого происхождения. Логика как наука основана Аристотелем (384-320 гг до н.э.), который был необыкновенной фигурой в целой плеяде блестящих греческих ученых. Он был последователем Платона и посещал его Академию в Афинах. После смерти Платона (347 г.до н.э.) Аристотель покинул Афины. Он вернулся туда 12 лет спустя и основал свою школу - Лицей. Одним из учеников Аристотеля был Александр Великий.

Аристотель не был математиком в полном смысле этого слова, его логика является скорее частью философии, но эта часть - основа всех наук. В своем выдающемся произведении "Аналитики" Аристотель создал и проверил около 20 схем рассуждений, которые назвал силлогизмами. Процитируем самый известный силлогизм: "Сократ - человек; все люди смертны; значит Сократ смертен". После Аристотеля силлогизмы и их трансформации стали основой дедуктивных рассуждений. Галилей говорил, что если бы ему пришлось начать снова свое будущее, то он последовал бы совету Платона и "принялся бы сперва за математику как науку, требующую точности и принимающую за верное то, что вытекает как следствие из доказанного".

Готфрид Лейбниц в начале XVIII века сделал попытку создать формальную логическую систему, введя законы сочетания высказываний. Он высказал идею о том, что рассуждения могут быть сведены к механическому выполнению определенных действий по установленным правилам: "Можно придумать некий алфавит человеческих мыслей, и с помощью комбинации букв этого алфавита и анализа слов, из них составленных, все может быть открыто и разрешимо". Но эти работы не были опубликованы, и лишь в XIX веке Джордж Буль и Август де Морган основали математическую логику, независимую от философии.

Назовем известнейшие работы Буля (1815-1864): "Формальная логика", "Исследование законов мысли". Буль вводит в логику алгебраическую структуру, называемую сегодня кольцо Буля, две операции, свойства которых в чем-то подобны свойствам операции с числами (например, 1+0=1), и в чем-то расходятся с ними (например, 1+1=1). Это позволило описать логику высказываний как формальную алгебраическую структуру.

Другой математик, А.де Морган, ввел кванторы (не называя их) и сделал попытку формального определения структур, продолжив работу, начатую Булем.

Логические или нечисловые задачи составляют обширный класс нестандартных задач. Сюда относятся, прежде всего, текстовые задачи, в которых требуется распознать объекты или расположить их в определенном порядке по имеющимся свойствам. При этом часть утверждений условия задачи может выступать с различной истинностной оценкой (быть истинной или ложной). К классу логических задач относятся также задачи на переливания и взвешивания (фальшивые монеты и т.п.).

Итак, я ставлю перед собой цель:

• показать различные способы решения логических задач;

• на примерах конкретных задач выяснить: какие методы более эффективные;

• продемонстрировать умение сравнивать и анализировать, составлять цепочки умозаключений и делать логические выводы.

Известно несколько различных способов решения логических задач:

• Метод рассуждений;

  • Метод таблиц;

  • Метод графов;

  • Метод блок-схем;

  • Метод бильярда;

  • Метод кругов Эйлера.

Остановимся отдельно на каждом из выделенных методов, иллюстрируя их примерами решения конкретных задач.

Метод первый: Метод рассуждений

Идея метода: Последовательные рассуждения и выводы из утверждений, содержащихся в условии задачи.

Способ рассуждений - самый примитивный способ. Этим способом решаются самые простые логические задачи. Его идея состоит в том, что мы проводим рассуждения, используя последовательно все условия задачи, и приходим к выводу, который и будет являться ответом задачи. Познакомиться с этим методом можно на следующем примере. Этим способом обычно решают несложные логические задачи.

Задача .

Директор школы беседует с 4 учениками школы, подозреваемыми в хищении классного журнала из учительской. Александр сказал, что журнал похитил Борис. Борис утверждал, что виноват Григорий. Григорий заверил директора, что Борис врет. Виктор настаивал на том, что журнал взял не он. Директору школы удалось установить, что один из учащихся сказал все же правду. Кто похитил журнал?

Решение. Т.к. правду сказал только один из учащихся, предположим, что журнал украл Александр. Тогда правду сказали 2 учащихся Григорий и Виктор. А это противоречит условию. Пусть журнал украл Борис. Вновь правду сказали двое: Александр и Григорий. Пришли к противоречию. Пусть журнал украл Григорий. Вновь правду сказали двое: Александр и Борис. Остается один ученик - Виктор, который и украл журнал. Все при этом лгут, только Григорий говорит правду.

Метод второй: Метод таблиц

Основной прием, который используется при решении текстовых логических задач, заключается в построении таблиц. Таблицы не только позволяют наглядно представить условие задачи или ее ответ, но в значительной степени помогают делать правильные логические выводы в ходе решения задачи.

Задача.

На столе в один ряд стоят четыре вазы разного цвета (черного, синего, зеленого и белого). В каждой вазе находятся цветы только одного из видов: тюльпаны, розы, лилии и гвоздики.

Решение. Известно, что тюльпаны и розы стоят не в белой вазе. Ваза с лилиями стоим между синей вазой и вазой с гвоздиками. В черной вазе не лилии и не тюльпаны. Зеленая ваза стоит около черной вазы и вазы с розами. Укажите,

какие цветы стоят в каких по цветы вазах.

Составим таблицу:

Метод третий: Метод графов

Слово «граф» в математической литературе появилось совсем недавно. Понятие графа используется не только в математике, но и в технике и даже в повседневной жизни под разными названиями - схема, диаграмма.

Особенно большую помощь графы оказывают при решении логических задач. Представляя изучаемые объекты в наглядной форме, «графы» помогают держать в памяти многочисленные факты, содержащиеся в условии задачи, устанавливать связь между ними.

Графом называется любое множество точек, некоторые из которых соединены линиями или стрелками. Точки, изображающие элементы множества, называют вершинами графа, соединяющие их отрезки - рёбрами графа. Точки пересечения рёбер графа не являются его вершинами. Во избежание путаницы вершины графа часто изображают не точками, а маленькими кружочками. Рёбра иногда удобнее изображать не прямолинейными отрезками, а дугами.

Задача.

На рисунке - схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?

Решение (перебор вершин по алфавиту):

1. Запишем вершины в алфавитном порядке и для каждой из них определим, из каких вершин можно в нее попасть

Б  А

В  АБГ

Г  А

Д  БВ

Е  Г

Ж  ВЕ

И  Д

К  ИДЖЕ

2. теперь определяем количество путей; сначала ставим 1 для тех вершин, в которые можно проехать только из начальной (А):

   вершина

   откуда?

   N

   Б

   А

   1

   В

   АБГ

   Г

   А

   1

   Д

   БВ

   Е

   Г

   Ж

   ВЕ

   И

   Д

   К

   ИДЖЕ

3. затем на каждом шаге добавляем те вершины, в которые можно доехать из уже добавленных в список (и из исходной точки):

Ответ: 13.

Метод четвертый - Метод кругов Эйлера

Это новый тип задач, в которых требуется найти некоторое пересечение множеств или их объединение, соблюдая условия задачи.

Круги Эйлера - геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления.

Метод Эйлера является незаменимым при решении некоторых задач, а также упрощает рассуждения. Однако прежде чем приступить к решению задачи, нужно проанализировать условие. Иногда с помощью арифметических действий решить задачу легче.

Задача:

Некоторые ребята из нашего класса любят ходить в кино. Известно, что 15 ребят смотрели фильм «Обитаемый остров», 11 человек - фильм «Стиляги», из них 6 смотрели и «Обитаемый остров», и «Стиляги». Сколько человек смотрели только фильм «Стиляги»?

Решение . Чертим два множества таким образом:

^ 6 человек, которые смотрели фильмы «Обитаемый остров» и «Стиляги», помещаем в пересечение множеств.

15 - 6 = 9 - человек, которые смотрели только «Обитаемый остров».

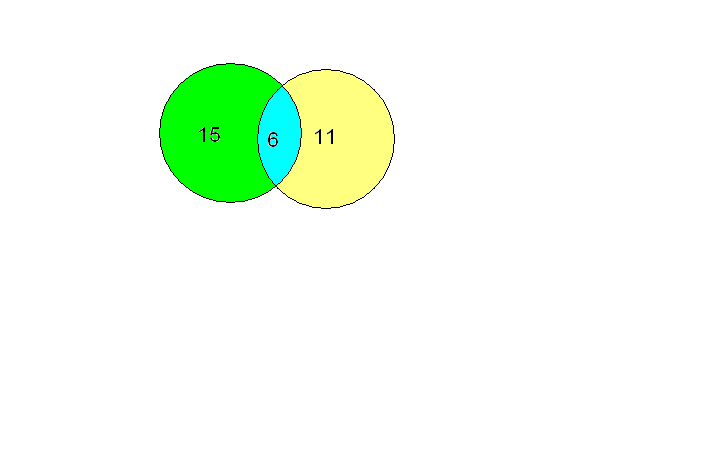
11 - 6 = 5 - человек, которые смотрели только Стиляги».

Ответ: 5 человек смотрели только «Стиляги».

Заключение.

Я старался показать, что математика - не сухая и скучная наука, а полная необычных и интересных открытий жизнь. Для решения подобных задач не нужны специальные теоретические знания, но необходимо мышление, умение сравнивать и анализировать, определять истинность суждений и строить умозаключения.

Литература.

В.И.Арнольд. Задачи для детей от 5 до 15 лет. -- 2-е изд., дополненное. --

М.: МЦНМО, 2007. -- 16 с.

Байиф Ж-К. Логические задачи. М.: Мир, 1983. 171 с.

Бизам Д., Герцег Я. Многоцветная логика. М.: Мир, 1978. 434 с.

Брадис М.В., Минковский В.Л., Харчева А.К. Ошибки в математических рассуждениях. М.: Учпедгиз, 1959. 176 с.

kpolyakov.narod.ru/school/ege.htm</ - сайт К.Полякова