Конспект занятия по математике на тему 'Конус'

Математика

(Название дисциплины /МДК)

Образовательное учреждение: ГАПОУ РО «Донской банковский колледж»

Преподаватель Драпеза Марина Андреевна

Тема урока: Конус. Свойства конуса параллельных основанию

Курс: 1

Цели урока:

1.Образовательная

способствовать формированию представления о конусе, сечениях конуса

2. Развивающая

способствовать развитию творческого мышления, развитию навыка

поиска и обработки информации, развитию пространственного мышления

3.Воспитательная

способствовать формированию интердисциплинарных связей математики,

развитию коммуникативных навыков

4.Методическая

совершенствовать методику проведения уроков, развивать творческое

отношение к образовательному процессу

Тип урока: урок по передаче и усвоению новых знаний

Вид урока: комбинированный

Межпредметная связь: техника, бытовые задачи

Учебно-методическое обеспечение: интерактивная доска, раздаточный

материал, модели геометрических тел

Структура урока:

1. Организационный момент (2 минуты)

2. Актуализация знаний (5 минут)

3. Объяснение нового материала (38 минут)

4. Закрепление изученного материала (37 минут)

5. Рефлексия (5 минут)

6. Постановка домашнего задания (3 минуты)

Ход урока

1. Организационный момент

Характер ориентировочных и исполнительских действий

В результате усвоения на этом уровне преподаватель/студент может

Преподаватель

Студенты

Приветствует студентов, отмечает отсутствующих, проверка готовности группы к занятию (наличие карандаша, линейки, элипса)

Приветствуют преподавателя

Цель урока: «Узнать, какое геометрическое тело называется конусом, его основные элементы»

2. Актуализация знаний

Проводит фронтальный опрос по теме «Цилиндр» (Приложение 1). Проверка осуществляется соседом по парте

Выполнение самостоятельной работы. Проверяют работу соседа

Актуализируют пройденный материал

3. Объяснение нового материала

В опросе вы вспомнили различные способы определения цилиндрической поверхности: через направляющую, как тело вращения, как предельный переход от n-угольной призмы. Аналогичным образом можно ввести понятие конуса.

Изображает конус, обращая внимание на правильность построения чертежа, описывает элементы конуса

Чертят конус, надписывают соответствующие элементы

Формирование верного представления о геометрическом теле и способах его изображения

Опишите способ получения конуса через окружность и образующие

Можно взять любую точку? Изменится ли от этого вид конуса?

Нами будет рассмотрен прямой круговой конус

Окружность лежит в плоскости. Берем точку и соединяем ее с каждой точкой окружности

Если взять точку, лежащую на перпендикуляре, проходящем через центр, то конус получится прямым, если не на перпендикуляре - наклонным

Формирование представления о данном способе описания конической поверхности

Опишите способ получения конуса как тело вращения

Назовите элементы прямоугольного треугольника и соответствующие им элементы конуса

Вращаем прямоугольный треугольник вокруг одного из катетов

Гипотенуза - образующая, катет, вокруг которого происходит вращение - высота, другой катет - радиус конуса

Формирование представления о данном способе описания конической поверхности

Осталось описать один способ получения. Если в цилиндре предельный переход n-угольной призмы, то, как вы считаете, из какого геометрического тела можно получить конус?

Отвечают на вопросы преподавателя (из пирамиды)

Формирование представления о данном способе описания конической поверхности

Рассмотрим сечения конуса плоскостью

Какие виды сечений мы рассматривали в цилиндре?

Эти же сечения мы будем рассматривать и в конусе.

Помимо вышеуказанных сечений часто рассматриваемыми являются также иные, так называемые конические сечения.

Осевое и параллельное основанию. Обсуждение вида осевого сечения, сечения, параллельного основанию, формул их площадей

Умение выстраивать цепочку доказательств

4. Закрепление изученного материала

Решение комплексной задачи с буквенными данными

Решение комплексных задач с числовыми данными

Решение задач (приложение 2, 4)

Умение применять полученные знания при решении задач

Решение задач самостоятельно

Индивидуальные карточки (приложение 3)

Первая цифра обозначает уровень сложности (1 - саамы легкий, 3 - самый сложный), вторая цифра номер варианта

5. Рефлексия

Повторение формул нахождения основных элементов конуса, типовые задачи.

6. Постановка домашнего задания

Студенты обмениваются карточками, которые и будут являться домашним заданием.

Приложение 1. Фронтальный опрос

ФИО___________________________________группа___________

1. Цилиндрическая поверхность через направляющую

____________________________________________________________________________________________________________________________________

2. Какую фигуру представляет из себя осевое сечение цилиндра?

____________________________________________________________________________________________________________________________________

ФИО___________________________________группа___________

1. Цилиндрическая поверхность как предельный переход n-угольной призмы

____________________________________________________________________________________________________________________________________

2. Какую фигуру представляет из себя сечение цилиндра, параллельное основанию?

____________________________________________________________________________________________________________________________________

ФИО___________________________________группа___________

1. Цилиндрическая поверхность как тело вращения

____________________________________________________________________________________________________________________________________

2. Площадь осевого сечения?

____________________________________________________________________________________________________________________________________

ФИО___________________________________группа___________

1. Площадь полной поверхности цилиндра

____________________________________________________________________________________________________________________________________

2. Площадь боковой поверхности цилиндра

____________________________________________________________________________________________________________________________________

Приложение 2

Конус имеет образующую l, радиус r и высоту h. Угол между образующей и плоскостью основания равен α, угол между образующими осевого сечения равен β.

Основные формулы:

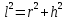
Для нахождения углов: прямоугольные треугольники, теорема косинусов.

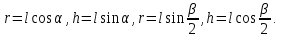
Площадь осевого сечения

Осевое сечение - равносторонний треугольник.

Площадь сечения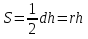

Площадь сечения, параллельного основанию

Если радиус основания конуса, а радиус сечения, параллельного основанию, 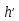- расстояние на котором проходит сечение, параллельное основанию (считая от основания), 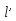- длина образующей от основания до сечения.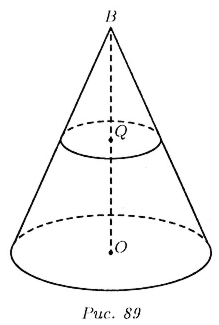

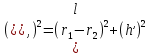
Приложение 3. Варианты индивидуальных карточек

Вариант 1-1

1. Высота конуса равна 12 см, радиус конуса равен 5 см. Найдите образующую конуса.

2. Образующая конуса, равная 14 см, наклонена к плоскости основания под углом 60⁰. Найдите радиус и высоту конуса.

3. Диаметр основания конуса равен 6 см, высота - 4 см. Найдите площадь осевого сечения.

Вариант 1-2

1. Высота конуса равна 15 см, радиус конуса равен 8 см. Найдите образующую конуса.

2. Образующая конуса, равная 14 см, наклонена к плоскости основания под углом 45⁰. Найдите радиус и высоту конуса.

3. Диаметр основания конуса равен 40 см, высота - 21 см. Найдите площадь осевого сечения.

Вариант 1-3

1. Высота конуса равна 4 см, радиус конуса равен 3 см. Найдите образующую конуса.

2. Образующая конуса, равная 16 см, наклонена к плоскости основания под углом 30⁰. Найдите радиус и высоту конуса.

3. Диаметр основания конуса равен 10 см, высота - 12 см. Найдите площадь осевого сечения.

Вариант 1-4

1. Высота конуса равна 21 см, радиус конуса равен 20 см. Найдите образующую конуса.

2. Образующая конуса, равная 16 см, наклонена к плоскости основания под углом 45⁰. Найдите радиус и высоту конуса.

3. Диаметр основания конуса равен 16 см, высота - 15 см. Найдите площадь осевого сечения.

Вариант 2-1

1. Высота конуса на 7 см больше его радиуса. Найдите радиус конуса и высоту, если образующая равна 13 см.

2. Образующая конуса, равная 14 см, наклонена к плоскости основания под углом 30⁰. Найдите площадь основания конуса.

3. Угол между образующими осевого сечения равен 60⁰. Найдите площадь осевого сечения, если радиус основания равен 12 см.

Вариант 2-2

1. Высота конуса на 7 см больше его радиуса. Найдите радиус конуса и высоту, если образующая равна 17 см.

2. Образующая конуса, равная 14 см, наклонена к плоскости основания под углом 45⁰. Найдите площадь основания конуса.

3. Угол между образующими осевого сечения равен 45⁰. Найдите площадь осевого сечения, если радиус основания равен 8 см.

Вариант 2-3

1. Высота конуса на 1 см больше его радиуса. Найдите радиус конуса и высоту, если образующая равна 5 см.

2. Образующая конуса, равная 16 см, наклонена к плоскости основания под углом 30⁰. Найдите площадь основания конуса.

3. Угол между образующими осевого сечения равен 30⁰. Найдите площадь осевого сечения, если радиус основания равен 6 см.

Вариант 2-4

1. Высота конуса на 1 см больше его радиуса. Найдите радиус конуса и высоту, если образующая равна 29 см.

2. Образующая конуса, равная 16 см, наклонена к плоскости основания под углом 45⁰. Найдите площадь основания конуса.

3. Угол между образующими осевого сечения равен 90⁰. Найдите площадь осевого сечения, если радиус основания равен 10 см.

Вариант 3-1

1. Высота конуса на 7 см больше его радиуса, а их произведение равно 60 см². Найдите высоту, радиус и образующую конуса.

2. Высота конуса равна длине окружности основания конуса радиуса 5 см. Найдите угол между образующей и плоскостью основания конуса.

3. Найдите высоту конуса, если площадь осевого сечения равна 8 см², а площадь основания равна 10 см².

Вариант 3-2

1. Высота конуса на 7 см больше его радиуса, а их произведение равно 120 см². Найдите высоту, радиус и образующую конуса.

2. Высота конуса равна длине окружности основания конуса радиуса 4 см. Найдите угол между образующей и плоскостью основания конуса.

3. Найдите высоту конуса, если площадь осевого сечения равна 15 см², а площадь основания равна 13 см².

Вариант 3-3

1. Высота конуса на 1 см больше его радиуса, а их произведение равно 12 см². Найдите высоту, радиус и образующую конуса.

2. Высота конуса равна длине окружности основания конуса радиуса 7 см. Найдите угол между образующей и плоскостью основания конуса.

3. Найдите высоту конуса, если площадь осевого сечения равна 14 см², а площадь основания равна 16 см².

Вариант 3-4

1. Высота конуса на 1 см больше его радиуса, а их произведение равно 420 см². Найдите высоту, радиус и образующую конуса.

2. Высота конуса равна длине окружности основания конуса радиуса 8 см. Найдите угол между образующей и плоскостью основания конуса.

3. Найдите высоту конуса, если площадь осевого сечения равна 12 см², а площадь основания равна 13 см².

Приложение 4. Комбинированные и практикоориентированные задачи

1. Коническим сверлом необходимо сделать отверстие в стене диаметром 4 см. Как глубоко необходимо сверлить, если известно, что при длине сверла 8 см диаметр его основания равен 6 см.

2. Пластину каких размеров (длина и высота) необходимо взять для того, чтобы путем ее вращения вокруг оси симметрии просверлить коническое отверстие диаметром 12 см, и площадью осевого сечения, равной 45% от площади основания.

3. Найдите площадь осевого сечения тела, полученного путем вращения прямоугольного треугольника вокруг гипотенузы, равной 29 см. Длина одного из катетов равна 20 см.

4. Какой процент о площади осевого сечения составляет площадь основания конуса, полученного путем вращения прямоугольного треугольника с катетами 3 см и 4 см вокруг большего из катетов.