рабочая программа по математике 8 класс

Пояснительная записка

Рабочая программа составлена на основе

• Федерального компонента государственных образовательных стандартов начального общего, основного общего и среднего (полного) общего образования

• Программы для общеобразовательных учреждений. Алгебра 7-9» (составитель:Т.А.Бурмистрова, М.: Просвещение, 2008)

• Программы для общеобразовательных учреждений. Геометрия 7-9» (составитель:Т.А.Бурмистрова, М.: Просвещение, 2008)

Изучение математики в 8 классе направлено на реализацию целей и задач, сформулированных в Государственном стандарте общего образования по математике:

- овладение системой математических знаний и умений, необходимых для применения в практической деятельности, продолжении образования;

- интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе, ясность и точность мысли, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей;

- воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса.

Требования к уровню подготовки установлены Государственным стандартом основного общего образования в соответствии с обязательным минимумом содержания.

В 8 классе курс математики делится на три раздела: алгебра - 102 часа, геометрия - 68 часов. На итоговое повторение учебного материала отводится 12 часов.

Количество часов: в неделю - 5, всего за год 170 часов, в том числе рассчитана на детей, занимающихся по программе VII вида.

В результате изучения курса математики 8 класса обучающиеся должны:

знать/понимать

• существо понятия математического доказательства; примеры доказательств;

• существо понятия алгоритма; примеры алгоритмов;

• как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;

• как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;

• как потребности практики привели математическую науку к необходимости расширения понятия числа;

• вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;

• каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждений о них, важных для практики;

• смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации;

Арифметика

уметь

• выполнять устно арифметические действия: сложение и вычитание двузначных чисел и десятичных дробей с двумя знаками, умножение однозначных чисел, арифметические операции с обыкновенными дробями с однозначным знаменателем и числителем;

• переходить от одной формы записи чисел к другой, представлять десятичную дробь в виде обыкновенной и в простейших случаях обыкновенную в виде десятичной, проценты - в виде дроби и дробь - в виде процентов; записывать большие и малые числа с использованием целых степеней десятки;

• выполнять арифметические действия с рациональными числами, сравнивать рациональные и действительные числа; находить в несложных случаях значения степеней с целыми показателями и корней; находить значения числовых выражений;

• округлять целые числа и десятичные дроби, находить приближения чисел с недостатком и с избытком, выполнять оценку числовых выражений;

• пользоваться основными единицами длины, массы, времени, скорости, площади, объема; выражать более крупные единицы через более мелкие и наоборот;

• решать текстовые задачи, включая задачи, связанные с отношением и с пропорциональностью величин, дробями и процентами;

использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

• решения несложных практических расчетных задач, в том числе c использованием при необходимости справочных материалов, калькулятора, компьютера;

• устной прикидки и оценки результата вычислений; проверки результата вычисления с использованием различных приемов;

• интерпретации результатов решения задач с учетом ограничений, связанных с реальными свойствами рассматриваемых процессов и явлений;

Алгебра

уметь

• составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;

• выполнять основные действия со степенями с целыми показателями, с многочленами и с алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;

• применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;

• решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним, системы двух линейных уравнений и несложные нелинейные системы;

• решать линейные и квадратные неравенства с одной переменной и их системы;

• решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;

• изображать числа точками на координатной прямой;

• определять координаты точки плоскости, строить точки с заданными координатами; изображать множество решений линейного неравенства;

• распознавать арифметические и геометрические прогрессии; решать задачи с применением формулы общего члена и суммы нескольких первых членов;

• находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;

• определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств;

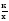• описывать свойства изученных функций (у=кх, где к0, у=кх+b, у=х², у=х³, у =,у=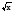), строить их графики;

использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

• выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами; нахождения нужной формулы в справочных материалах;

• моделирования практических ситуаций и исследовании построенных моделей с использованием аппарата алгебры;

• описания зависимостей между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций;

• интерпретации графиков реальных зависимостей между величинами.

Элементы логики, комбинаторики, статистики и теории вероятностей

уметь

• проводить несложные доказательства, получать простейшие следствия из известных или ранее полученных утверждений, оценивать логическую правильность рассуждений, использовать примеры для иллюстрации и контрпримеры для опровержения утверждений;

• извлекать информацию, представленную в таблицах, на диаграммах, графиках; составлять таблицы, строить диаграммы и графики;

• решать комбинаторные задачи путем систематического перебора возможных вариантов, вычислять средние значения результатов измерений;

• находить частоту события, используя собственные наблюдения и готовые статистические данные;

использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

• выстраивания аргументации при доказательстве (в форме монолога и диалога);

• распознавания логически некорректных рассуждений;

• записи математических утверждений, доказательств;

• анализа реальных числовых данных, представленных в виде диаграмм, графиков, таблиц;

• решения практических задач в повседневной и профессиональной деятельности с использованием действий с числами, процентов, длин, площадей, объемов, времени, скорости;

• решения учебных и практических задач, требующих систематического перебора вариантов;

• понимания статистических утверждений.

Геометрия

уметь

• пользоваться языком геометрии для описания предметов окружающего мира;

• распознавать геометрические фигуры, различать их взаимное расположение;

• изображать геометрические фигуры; выполнять чертежи по условию задач; осуществлять преобразования фигур;

• распознавать на чертежах, моделях и в окружающей обстановке основные пространственные тела, изображать их;

• в простейших случаях строить сечения и развертки пространственных тел;

• проводить операции над векторами, вычислять длину и координаты вектора, угол между векторами;

• вычислять значения геометрических величин (длин, углов, площадей, объемов), в том числе: для углов от 0 до 180 определять значения тригонометрических функций по заданным значениям углов; находить значения тригонометрических функций по значению одной из них, находить стороны, углы и площади треугольников, длины ломаных, дуг окружности, площадей основных геометрических фигур и фигур, составленных из них;

• решать геометрические задачи, опираясь на изученные свойства фигур и отношений между ними, применяя дополнительные построения, алгебраический и тригонометрический аппарат, идеи симметрии;

• проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их использования;

• решать простейшие планиметрические задачи в пространстве;

использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

• описания реальных ситуаций на языке геометрии;

• расчетов, включающих простейшие тригонометрические формулы;

• решения геометрических задач с использованием тригонометрии

• решения практических задач, связанных с нахождением геометрических величин (используя при необходимости справочники и технические средства);

• построений геометрическими инструментами (линейка, угольник, циркуль, транспортир).

Формы и методы, технологии обучения.

Ведущими методами обучения являются: объяснительный и репродуктивный методы, частично-поисковый, метод математического моделирования, аксиоматический метод. На уроках используются элементы следующих технологий: личностно ориентированное обучение, обучение с применением опорных схем, дифференцированного обучения, ИКТ. Используются такие формы организации деятельности, как фронтальный опрос, групповая, парная и самостоятельная работа, работа с учебником, таблицами и др. учебными пособиями.

Используемые формы, способы и средства проверки и оценки результатов обучения.

1. Письменный контроль (самостоятельные и контрольные работы, проверка домашнего задания);

2. Тестовый (тестирование);

3. Математический диктант;

4. Устный опрос (собеседование)

Критерии и нормы оценивания знаний и умений учащихся по математике.

Критерии ошибок:

К г р у б ы м ошибкам относятся ошибки, которые обнаруживают незнание учащимися формул, правил, основных свойств, теорем и неумение их применять; незнание приемов решения задач, рассматриваемых в учебниках, а также вычислительные ошибки, если они не являются опиской;

К н е г р у б ы м ошибкам относятся: потеря корня или сохранение в ответе постороннего корня; отбрасывание без объяснений одного из них и равнозначные им;

К н е д о ч е т а м относятся: нерациональное решение, описки, недостаточность или отсутствие пояснений, обоснований в решениях

Оценка устных ответов учащихся по математике

Ответ оценивается отметкой «5», если ученик:

- полно раскрыл содержание материала в объеме, предусмотренном программой и учебником,

- изложил материал грамотным языком в определенной логической последовательности, точно используя математическую терминологию и символику;

- правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;

- показал умение иллюстрировать теоретические положения конкретными примерами, применять их в новой ситуации при выполнении практического задания;

- продемонстрировал усвоение ранее изученных сопутствующих вопросов, сформированность и устойчивость используемых при отработке умений и навыков;

- отвечал самостоятельно без наводящих вопросов учителя. Возможны одна - две неточности при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил по замечанию учителя.

Ответ оценивается отметкой «4», если он удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:

- в изложении допущены небольшие пробелы, не исказившие математическое содержание ответа;

- допущены один - два недочета при освещении основного содержания ответа, исправленные по замечанию учителя;

- допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные по замечанию учителя.

Отметка «3» ставится в следующих случаях:

- неполно или непоследовательно раскрыто содержание материала, но показано общее понимание вопроса и продемонстрированы умения, достаточные для дальнейшего усвоения программного материала (определенные «Требованиями к математической подготовке учащихся»);

- имелись затруднения или допущены ошибки в определении понятий, использовании математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;

- ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;

- при знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.

Отметка «2» ставится в следующих случаях:

- не раскрыто основное содержание учебного материала;

- обнаружено незнание или непонимание учеником большей или наиболее важной части учебного материала;

- допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.

Оценка письменных работ учащихся по математике

Отметка «5» ставится, если:

работа выполнена полностью;

в логических рассуждениях и обосновании решения нет пробелов и ошибок;

в решении нет математических ошибок (возможна одна неточность, описка, не являющаяся следствием незнания или непонимания учебного материала).

Отметка «4» ставится, если:

работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);

допущена одна ошибка или два-три недочета в выкладках, рисунках, чертежах или графиках (если эти виды работы не являлись специальным объектом проверки).

Отметка «3» ставится, если:

допущены более одной ошибки или более двух-трех недочетов в выкладках, чертежах или графиках, но учащийся владеет обязательными умениями по проверяемой теме.

Отметка «2» ставится, если:

допущены существенные ошибки, показавшие, что учащийся не владеет

обязательными умениями по данной теме в полной мере

Оценивание контрольных работ 5- 11 классы

Каждый вариант контрольной работы выстроен по одной схеме: задания базового (обязательного) уровня - до первой черты, задания уровня выше среднего - между первой и второй чертой, задания повышенной сложности - после второй черты.

Шкала оценок за выполнение контрольной работы выглядеть так:

- за успешное выполнение заданий до первой черты - оценка 3;

- за успешное выполнение заданий базового уровня и одного дополнительного (после первой или второй черты) - оценка 4;

- за успешное выполнение задание трех уровней - оценка 5.

При этом оценку не рекомендуется снижать за одно неверное решение или погрешности в базовой части работы (допустимый люфт)

Математический диктант, включающий в себя 8-10 примеров для проверки вычислительных навыков:

«5» - все выполнено верно, не более одного недочета;

«4» - не выполнена 1/5 часть задания;

«3» - не выполнена 1/4 часть задания;

«2» - не выполнена 1/2 часть задания.

Комбинированная работа, включающая в себя задачи, уравнения, неравенства, вычисление значений выражений:

«5» ставится при безошибочном решении задач и примеров;

«4» ставится, если в задачах иди в примерах или при выполнении других заданий допущены 1-2 грубые или 4 негрубые ошибки;

«3» ставится, если в задачах, или в примерах, а также при выполнении других заданий допущено не более 5 грубых или 8 негрубых ошибок;

«2» ставится, если в одной или в обеих частях работы допущено более 5 грубых или более 8 негрубых ошибок.

Самостоятельные работы по дифференцированным заданиям следует оценивать по общепринятым критериям оценочной системы (см. выше).

При оценке работ, состоящих только из задач (если обе задачи равнозначны):

«5» ставится, если правильно решены обе задачи;

«4» ставится, если при правильном ходе решения обеих задач допущена 1 ошибка в вычислениях;

«3» ставится, если:

а) при правильном ходе решения обеих задач допущены 2 -3 грубые ошибки; б) если одна задача решена правильно, а в другой ошибка в ходе решения;

«2» ставится, если в обеих задачах неверный ход решения. Если первая задача является, с точки зрения учителя, основной, а вторая дополнительной, то оценка «3» может быть поставлена, если вторая задача не решена или решена ошибочно. Если не решена основная задача, то ставится оценка «2».

При оценке работ, состоящих из трех задач

«5» ставится за правильное решение трех, задач;

«4» ставится за правильное решение двух задач;

«3» ставится, если одна задача решена правильно полностью, а в других задачах допущена ошибка в вычислениях, либо решение незакончено, пропущено действие и др.

Если же две задачи решены неправильно (и среди них более сложная), то в таком случае ставится «2».

ПЕРЕЧЕНЬ УМК

Предмет по учебному плану

класс

Учебник (автор,наименование, год издания, изд-во)

Кол-во часов

УМК

МАТЕМАТИКА

8 базовый

Ю.Н.Макарычев, Н.Г.Миндюк, К.И.Нешков, С.Б.Суворова, Алгебра-8 (базовый уровень), 2009-2013г.г, Просвещение

3

-Т.А.Бурмистрова «Программы для общеобразовательных учреждений. Алгебра 7-9 класс», М.Просвещение, 2008 г.

- А.Н.Рурукин, «Поурочные разработки по Алгебре», М.ВАКО 2013г (электронный вариант)

- Л.И.Звавич, Л.В.Кузнецова, С.Б.Суворова «Дидактические материалы по алгебре», М.Просвещение, 2008г.

- Ю.Н.Макарычев, Н.Г.Миндюк, К.И.Нешков, С.Б.Суворова, И.С.Шлыкова «Изучение алгебры в 7-9 классах», М.Просвещение,2009г,(электронный вариант)

- Ю.Н.Макарычев, Н.Г.Миндюк «Алгебра элементы статики и теории вероятностей», Просвещение, 2005г.(электронный вариант)

Л.С.Атанасян, Л.В.Бутузов и др., Геометрия 7-9(базовый уровень), 2009-2011г.г., Просвещение

2

- Т.А.Бурмистрова «Программы для общеобразовательных учреждений. Геометрия 7-9 класс», М.Просвещение, 2008 г.

- Н.Ф.Гаврилова «Поурочные разработки по Геометрии», М.Вако,2010г.(электронный вариант)

-Б.Г.Зив, В.М.Мейлер «Дидактические материалы по геометрии», Просвещение, 2013г.

Тематический план 8 класс «Алгебра»

№

Наименование разделов

Количество

часов

I

Рациональные дроби

23

II

Квадратные корни

19

III

Квадратные уравнения

21

IV

Неравенства

20

V

Степень с целым показателем.

Элементы статистики

11

VI

Итоговое повторение

8

ИТОГО

102

Тематический план 8 класс «Геометрия»

№

Наименование разделов

Количество

часов

I

Четырёхугольники

14

II

Площадь

14

III

Подобные треугольники

19

IV

Окружность

17

V

Повторение. Решение задач.

4

ИТОГО

68

контрольные работы по математике в 8 классе:

Календарно-тематическое планирование

№ п.п

Наименование разделов, тем

всего часов

из них

лабораторные и практические работы

Контрольный и диагностический материал

Глава I.

Рациональные дроби

23

2

1

2

Рациональные дроби и их свойства.

5

Глава I

Четырёхугольники

14

1

3

4

Многоугольник.

2

5

6

7

Рациональные дроби и их свойства

8

9

Параллелограмм и трапеция

6

10

11

12

Сумма и разность дробей

6

13

14

Параллелограмм и трапеция

15

16

17

Сумма и разность дробей

18

19

Параллелограмм и трапеция

20

Контрольная работа № 1

«Сокращение дробей. Сложение и вычитание рациональных дробей»

1

1

21

22

Произведение и частное дробей

10

23

24

Прямоугольник, ромб, квадрат

4

25

26

27

Произведение и частное дробей

28

29

Прямоугольник, ромб, квадрат

30

31

32

Произведение и частное дробей

33

Решение задач

1

34

Контрольная работа № 2

«Четырёхугольники».

1

1

35

36

Произведение и частное дробей

37

Контрольная работа № 3

«Рациональные дроби».

1

1

Глава II

Площадь

14

1

38

39

Площадь многоугольника

2

Глава II

Квадратные корни

19

2

40

41

Действительные числа

2

42

Арифметический квадратный корень.

5

43

44

Площадь параллелограмма, треугольника и трапеции

6

45

46

47

Арифметический квадратный корень.

48

49

Площадь параллелограмма, треугольника и трапеции

50

Арифметический квадратный корень.

51

52

Свойства арифметического квадратного корня.

3

53

54

Площадь параллелограмма, треугольника и трапеции

55

Свойства арифметического квадратного корня.

56

Контрольная работа №4

«Свойства квадратного корня»

1

1

57

Применение свойств арифметического квадратного корня.

7

58

59

Теорема Пифагора

3

60

61

62

Применение свойств арифметического квадратного корня.

63

Теорема Пифагора

64

Решение задач

2

65

66

67

Применение свойств арифметического квадратного корня.

68

Решение задач

69

Контрольная работа № 5

«Площадь».

1

1

70

Контрольная работа№6

«Квадратные корни».

1

1

Глава III

Квадратные уравнения

21

2

71

72

Квадратное уравнение и его корни

10

Глава III

Подобные треугольники

19

2

73

Определение подобных треугольников

2

74

Определение подобных треугольников

75

76

77

Квадратное уравнение и его корни

78

79

Признаки подобия треугольников

5

80

81

82

Квадратное уравнение и его корни

83

84

Признаки подобия треугольников

85

86

Квадратное уравнение и его корни

87

Контрольная работа №7

«Квадратное уравнение и его корни»

1

1

88

Признаки подобия треугольников

89

Контрольная работа № 8

« Признаки подобия треугольников ».

1

1

90

91

92

Дробные рациональные уравнения.

9

93

94

Применение подобия к доказательству теорем и решению задач

7

95

96

97

Дробные рациональные уравнения.

98

99

Применение подобия к доказательству теорем и решению задач

100

101

102

Дробные рациональные уравнения.

103

104

Применение подобия к доказательству теорем и решению задач

105

Контрольная работа №9

«Квадратные уравнения»

1

1

Глава IV

Неравенства

20

2

106

107

Числовые неравенства и их свойства

8

108

Применение подобия к доказательству теорем и решению задач

109

Соотношения между сторонами и углами треугольника

3

110

111

112

Числовые неравенства и их свойства

113

Соотношения между сторонами и углами треугольника

114

Соотношения между сторонами и углами треугольника

115

116

117

Числовые неравенства и их свойства

118

Контрольная работа № 10

«Подобные треугольники».

1

1

Глава IV

Окружность

17

1

119

Касательная к окружности

3

120

Контрольная работа № 11

«Свойства числовых неравенств»

1

1

121

122

Неравенства с одной переменной и их системы

10

123

124

Касательная к окружности

125

126

127

Неравенства с одной переменной и их системы

128

129

Центральные и вписанные углы

4

130

131

132

Неравенства с одной переменной и их системы

133

134

Центральные и вписанные углы

135

136

Неравенства с одной переменной и их системы

137

Контрольная работа №12

«Неравенства с одной переменной и их системы»

1

1

138

139

Четыре замечательные точки треугольника

3

Глава V

Степень с целым показателем. Элементы статистики

11

1

140

141

142

Степень с целым показателем и и её свойства

6

143

Четыре замечательные точки треугольника

144

Вписанная и описанная окружность

4

145

146

147

Степень с целым показателем и и её свойства

148

149

Вписанная и описанная окружность

150

Контрольная работа №13

«Степень с целым показателем и её свойства»

1

1

151

152

Элементы статики

4

153

Вписанная и описанная окружность

154

Решение задач

2

155

156

Элементы статики

157

Решение задач

158

Контрольная работа №14

«Окружность».

1

1

ПОВТОРЕНИЕ

8+4

159

Повторение. Решение задач по теме «Четырехугольники»

160

Повторение. Одночлен. Многочлен. Действия с многочленами.

161

Повторение. Способы разложения на множители.

162

Повторение. Решение задач с помощью уравнений и систем уравнений.

163

Повторение. Решение задач по теме «Подобные треугольники.»

164

Повторение. Решение задач по теме «Окружность»

165

Повторение. «Рациональные дроби

166

Повторение «Квадратные корни», «Квадратные уравнения»,

167

Повторение. Неравенства

168

Повторение. Решение задач. Подобные треугольники

169

Итоговый зачет

170

Итоговая контрольная работа №15

1

1

ИТОГО:

170

15

Лист фиксирования изменений и дополнений в Рабочей программе

Дата внесения

изменений

Содержание

Реквизиты документа (дата, № приказа)

Подпись лица, внесшего запись