План конспект урока по теме Объем шара и площадь сферы

Министерство образования и науки Краснодарского Края

ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ПРОФЕССИОНАЛЬНОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

Краснодарского Края

«КРАСНОДАРСКИЙ ТОРГОВО-ЭКОНОМИЧЕСКИЙ КОЛЛЕДЖ»

План-конспект урока:

«Объем шара и площадь сферы».

Преподаватель математики

Хромых А.Н.

Тема урока: Объем шара и площадь сферы

Цели урока:

образовательные:

обобщить и систематизировать знания обучающихся по теме «Тела вращения»; вывести формулу объема шара и площади сферы.

воспитательные:

показать, что источник возникновения изучаемой темы - реальный мир, что она возникла из практических потребностей; воспитание вычислительных навыков;

показать связь с историей; воспитание самостоятельности; воспитание стремления к самореализации.

развивающие:

совершенствование, развитие, углубление знаний, умений и навыков по теме; развитие пространственного воображения; развитие мыслительной деятельности: умения анализировать, обобщать, классифицировать.

Тип урока: Комбинированный

Методы и приемы: словесный, наглядный, фронтальный, индивидуальный, проблемный

Технологии:

Оборудование: учебник геометрии 10-11класс, автор Л.С.Атанасян; мультимедейный проектор; модели тел вращения (шар, цилиндр, конус); презентация.

План урока.

1.Организационный момент

2.Повторение.

3.Изучение нового материала.

4.Решение кроссворда

5.Первичное осмысление и закрепление новых знаний (практическая работа) - 15 минут.

6.Решение задач

7.Постановка домашнего задания

8.Подведение итогов урока

Ход урока

I. Организационный момент.

Сообщить тему урока, сформулировать цели урока.

II. Актуализация опорных знаний.

Теоретический опрос (фронтальная работа с обучающимися)

1) Устная работа. Соотнесите название фигуры и формулу объема и площади поверхности тел.1.Цилиндр. 2.Конус. 3.Усеченный конус. 4. Шар.

V=1/3S_ОСНH=1/3∏R²H V=S_ОСНH=πR²H V=1/3∏H(R²⁺r²⁺Rr) S=4 πR²

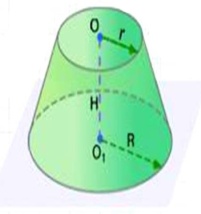
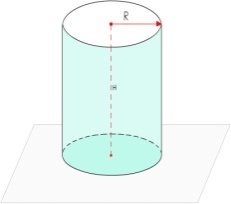
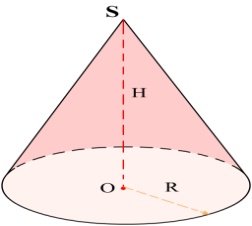
III. Изучение новой темы.

Сегодня мы с вами выведем формулу для вычисления объема шара.

Вспомните, определение шара и его элементов.

Шаром называется множество всех точек пространства, находящихся от данной точки на расстоянии, не больше данного R.

Радиусом шара называют всякий отрезок, соединяющий центр шара с точкой шаровой поверхности.

Отрезок, соединяющий две точки шаровой поверхности и проходящий через центр шара, называется диаметром шара.

Концы любого диаметра шара называются диаметрально противоположными точками шара. Отрезок, соединяющий две любые точки шаровой поверхности и не являющийся диаметром шара, называют хордой шара.

Теорема: Объем шара равен

Доказательство:

Мы уже знаем, что можно вычислять объёмы тел с помощью интегральной формулы

V=

Давайте посмотрим, как это можно сделать для вывода формулы объема шара.

(Учитель объясняет вывод формулы объёма шара с помощью формулы, ученики делают записи в тетрадях).

Рассмотрим шар радиуса R с центром в точке О и выберем ось ОХ произвольным образом (рис192).Сечение шара плоскостью, перпендикулярной к оси ОХ и проходящий через точку М этой оси, является кругом с центом в точке М. Обозначим радиус этого круга через r, а его площадь через S(х), где х абсцисса точки М. Выразим S(х) через х и R. Из прямоугольного треугольника ОМС находим . Тогда , где

Так как , то заменяя r через выражение получим

Заметим, что эта формула верна для любого положения точки М на диаметре АВ, т.е. для всех х, удовлетворяющих условию

Применяя основную формулу для вычисления объемов тел при а= -R, b=R, получим

Теорема доказана.

В практических приложениях часто указывается диаметр шара, поэтому в процессе решения задач полезно знать формулу , где D - диаметр шара

Решение кроссворда

IV.Формирование умений и навыков учащихся.

ПРОБЛЕМНАЯ ЗАДАЧА: При уличной торговле арбузами весы отсутствовали. Однако выход был найден: арбуз диаметром 3 дм приравнивали по стоимости к трём арбузам диаметром 1 дм.

Что вы возьмете? Правы ли были продавцы

Решение:

Необходимо найти объемы данных арбузов.

и таких арбузов три, значит их общий объем равен

Задача (Архимеда): На надгробном камне могилы Архимеда в Сиракузах изображен цилиндр с вписанным в него шаром. Это символ открытия формул объема шара и площади сферы, а также важного вывода, что «объем шара, вписанного в цилиндр в …раз меньше объема цилиндра и что также относятся площади поверхностей этих тел». Найдите отношение объема цилиндра к объему шара и отношение площади поверхности цилиндра к площади поверхности шара.

Дано: в цилиндр вписан шар

Найти: отношение объёмов цилиндра и шара, отношение площадей поверхностей

РЕШЕНИЕ:

Ответ:1,5

Одним из своих наивысших достижений Архимед считал доказательство того, что объём шара в полтора раза меньше объёма описанного около него цилиндра. Недаром шар, вписанный в цилиндр, был высечен на надгробии Архимеда в Сиракузах.

ПРАКТИЧЕСКАЯ РАБОТА «Вычисление объёмов тел вращения»

Задачи :

1.Около шара описан цилиндр, площадь поверхности

которого равна 18. Найдите площадь поверхности шара.

Решение: (Опираемся на открытие Архимеда)

Ответ: 12

2.Площадь поверхности шара уменьшили 9 раз. Во сколько раз уменьшился объем шара?

Решение:

Пусть радиус первого шара R, а уменьшенного r.

Поверхность шара S₁ = 4пR², стала S₂ = 4пR²/9 = 4п (R/3)² = 4пr²

Видим, что r =, т.е. радиус уменьшился в 3 раза.

Объем V₁= 4/3 ПR³, а объем V₂= 4/3 пr³ = 4/3 п(R/3)³ =4/3 пR³ /27 = V₁ / 27.

Ответ:27

V. Итог урока.

Оценить работу обучающихся на уроке и выставить оценки.

На сегодняшнем уроке мы с вами вывели формулу объема шара, выяснили, что данные тела имеют широкое практическое применение и сделали небольшое открытие, которое еще в 3 веке до нашей эры сделал Архимед.

Беседа по следующим вопросам:

Что было интересного сегодня на уроке?

Что вызвало трудности?

Какие умения приобрели сегодня?

Где могут пригодиться эти умения?

Домашнее задание.

П.82, №710

Домашнее задание.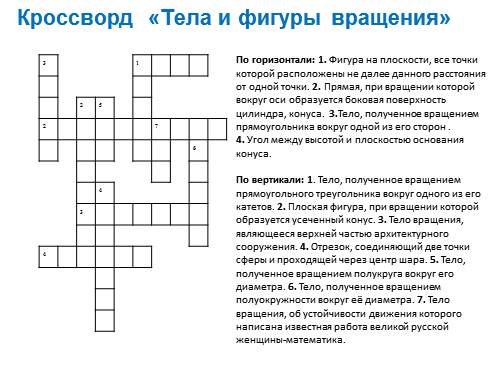

П.82 № 710, II уровень №713