• из двух правильных многоугольников с равными периметрами больше площадь того, у которого больше сторон

Таким образом, чем «ближе» многоугольник к кругу, тем, действительно, больше его изопериметрическое частное.

3. Миф о Дидоне.

В римской мифологии есть легенда о Дидоне. Согласно этой легенде, Дидона была дочерью царя Тира и женой жреца Геракла Акербаса. После того как брат Дидоны Пигмалион убил ее мужа, позарившись на его богатства, Дидона была вынуждена бежать. Захватив с собой часть сокровищ мужа, она в сопровождении многочисленных спутников отправилась на запад вдоль берегов Средиземного моря. Ей приглянулось одно место на побережье нынешнего Тунисского залива. Дидона повела переговоры с берберийским царем Ярбом о продаже земли. По условию она могла взять столько земли, сколько можно «окружить бычьей шкурой». Сделка состоялась. Тогда Дидона разрезала эту шкуру на тонкие ремни, связав их воедино, и окружила изрядный кусок земли. На этом месте была основана цитадель Карфагена Бирсу. (По-гречески «бирсу» как раз и означает «шкура».)

Так гласит легенда.

Этот эпизод дает повод задуматься над вопросом: сколько же земли можно окружить бычьей шкурой?

Задача Дидоны относится к изопериметрическим задачам, то есть к задачам на нахождение фигур заданного периметра, имеющих наибольшую или наименьшую площадь. Догадалась ли Дидона, что искомая фигура - круг? Кто знает... Известно лишь, что легендарная царица и на этот раз сумела урвать лишний кусок - она выбрала свой участок на берегу моря, так что вся морская граница досталась ей даром. За этой женщиной придется признать крупный геометрический талант: ведь изопериметрическая задача строго была решена лишь в прошлом веке швейцарским геометром Якобом Штейнером, а ее «карфагенский вариант» - с учетом того, что часть замкнутой кривой представляет собой прямую линию «побережья», - и того позже. Штейнер доказал - притом сразу пятью разными способами, - что именно круг охватывает самую большую площадь при данной длине замкнутой линии. Вслед за этим удалось выяснить, что следующее слово за правильными многоугольниками: они «выгоднее» любой другой фигуры с тем же числом сторон. Так была окончательно решена задача, которой, кроме легендарной Дидоны, занимались реальные ученые - например, Зенодор и Архимед.

Формулировки задачи Дидоны или классической изопериметрической задачи:

1. Среди замкнутых плоских кривых, имеющих заданную длину, найти кривую, охватывающую максимальную площадь.

2. Среди замкнутых плоских кривых, имеющих заданную площадь, найти кривую, имеющих минимальный периметр.

4.Метод Якоба Штейнера.

Среди всевозможных плоских замкнутых линий заданной длины найдите ту, которая ограничивает фигуру наибольшей площади.

Решение.

1. Фигура наибольшей площади с заданным периметром - выпуклая. В противном случае мы могли бы построить линию той же длины, ограничивающую фигуру большей площади (рис.6).

2. Если прямая делит пополам периметр фигуры, то она делит пополам и площадь фигуры. Пусть прямая АВ (А и В - точки на границе, рис.7) делит пополам периметр фигуры, но при этом одна из двух частей имеет большую площадь.

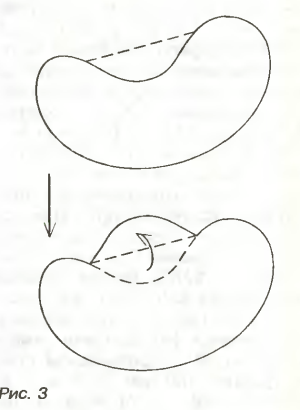
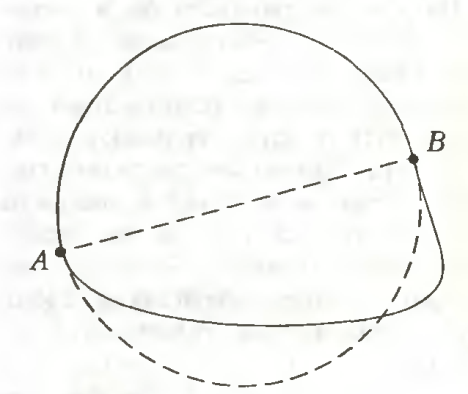
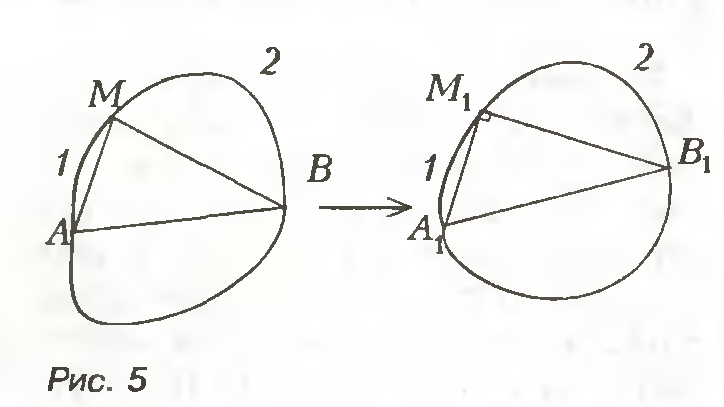
Рисунок 6 Рисунок 7 Рисунок 8

Заменим меньшую часть фигурой, симметричной большей относительно прямой АВ При этом площадь фигуры увеличится, а периметр не изменится.

Пусть М -(∙) AMB, МА и МВ (рис.8). Докажем, что

Предположим, что это не так. Проведем отрезки AM, MB и АВ, они разрежут нашу фигуру на четыре части. Построим новую фигуру :

1) Δ A₁ M₁ B₁ - прямоугольный, где A₁ M₁ = AM, М₁ B₁ = MB, < A₁ M₁ B₁ =90°.

2) Приставим к его катетам сегменты, равные сегментам 1 и 2 (см. рис.8)

3) Отразим все относительно гипотенузы A₁ B₁.

4) Получим новую фигуру с тем же периметром и большей площадью. S _{Δ A1 M1 B1} >S _{Δ АМВ}. Итак, мы доказали, что если прямая АВ делит пополам периметр фигуры с наибольшей площадью, М - произвольная точка на границе, отличная от А и В, то <AMB = 90°, т.е. М окружности с диаметром АВ. Таким образом, решение изопериметрической задачи дает окружность.

На самом деле Якоб Штейнер доказал, что если фигура наибольшей площади среди всех фигур данного периметра существует, то это - круг.

С изопериметрической задачи по существу начинается одно из важнейших направлений современной математики - вариационное исчисление.

4.Практическая часть

В ходе исследования провожу следующие эксперименты.

Эксперимент 1.

Отмотаем от катушки кусочек нити длиной 50 см.. Отрежем его и свяжем концами. Положим эту связанную нить на лист бумаги. Получилась плоская замкнутая кривая.

Выяснить: как следует положить нашу нить, чтобы она охватывала наибольшую площадь?

Рассчитать площади фигур с одним и тем же периметром.

1. Площадь круга, если С=50 см. (С - длина окружности)

Используем формулы S = π∙R², С = 2π∙R. Тогда R=C:2π, S = С² : 4π, S = 199 см².

2. Площадь полукруга, если l = 50 см. (l -длина полуокружности)

Используем формулу S = π∙R², C=l∙2= 100см, R =C:2π, S = С² : π. Значит, S_полукр=0,5∙S_кр

3. Площадь квадрата, Р = 50 см. (Р - периметр квадрата)

Используем формулы S = а², Р = 4а. Тогда а=Р:4, S = Р² :16, S = 156,25 см².

4. Площадь шестиугольника, Р = 50 см. (Р - периметр шестиугольника)

Используем формулы , Р = 6а. Тогда а=Р:6, S = 177 см².

5. Площадь равностороннего треугольника, Р = 50 см. (Р - периметр треугольника)

Используем формулы 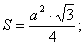Р = 3а. Тогда а=Р:3, S = 110 см².

6. Площадь равнобедренного прямоугольного треугольника, Р = 50 см.

(Р - периметр треугольника)

Используем формулы S = 0,5∙ a², Р = 2а+с. Тогда S = 107,5 см².

В ходе эксперимента я получила диаграмму.

Диаграмма 1. Площади фигур равного периметра (50 см).

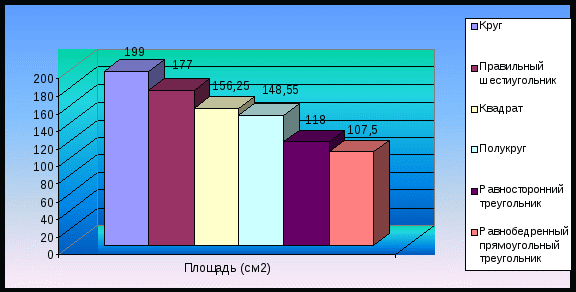
ВЫВОД:

Из перечисленных фигур, имеющих равный периметр, наибольшую площадь имеет круг.

Нить, охватывающая наибольшую площадь, надо положить так, чтобы получилась окружность.

Эксперимент 2.

Из данных фигур равной площади выявить фигуру с наименьшим периметром.

Результаты эксперимента занесены в диаграмму 2.

Диаграмма 1. Периметры фигур равной площади (1 см²).

ВЫВОД:

Из шести перечисленных фигур круг, указанный первым, имеет наименьший периметр.

Эксперимент 3.

Можно ли в листе бумаги размером с обычную страницу из тетради проделать такое отверстие, чтобы сквозь него мог пройти человек?

Выяснила, что если лист бумаги разрезать так, что при растяжении данной модели в результате можно получить окружность, - ответ утвердительный.

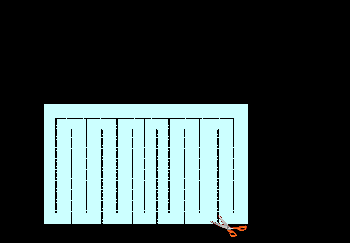
В итоге я получила, что круг - идеальная фигура.

Возвращаясь к задаче царицы Дидоны, рассчитаем территорию, которую заняла Дидона.

Площадь шкуры равна 35800 см². Разрежем ее на полоски шириной 0,5 см, тогда длина полуокружности равна будет 71600 см или 716 м.

С=2πR, C:2=πR, R=716:3,14≈228(м)

Sкруга=πR², S круга =3,14∙228²≈163230(м²)

S полукруга=Sкруга: 2=81615(м²)

На площади 81615 м² действительно можно построить крепость.

Задача о Пахоме.

Рассказ Л.Толстого о Пахоме: «крестьянин Пахом, который мечтал о собственной земле и собрал, наконец, желанную сумму, предстал перед требованием старшины: «Сколько за день земли обойдешь, вся твоя будет за 1000р. Но если к заходу солнца не возвратишься на место, с которого вышел, пропали твои деньги». Выбежал утром Пахом, прибежал на место и упал без чувств, обежав четырехугольник периметром Р=40 км.»

P=AB+BC+CD+AD=40

S=(2+10)/2*13=78

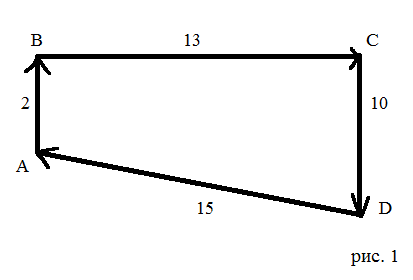
Составим таблицу для вычисления площадей прямоугольников с различными длинами сторон:

Стороны а

b

1

19

2

18

5

15

6

14

8

12

10

10

Площадь S

19

36

75

84

96

100

Вывод. Из всех прямоугольников данного периметра наибольшую площадь имеет квадрат. Пахом, например, мог бы пройти всего 36 км и иметь участок площадью 81 км²

Изучив изопериметрическую теорему на плоскости можно доказать изопериметрическую теорему в пространстве: «Из всех тел равного объема наименьшую поверхность имеет шар».

Исследование комфортности национальных жилищ с помощью изопериметрической теоремы.

Формула для вычисления комфортности жилища:

К - изопериметрический коэффициент;

V - объём жилища;

S - площадь поверхности

Какое из окружающих нас жилищ наиболее комфортно?

1.Яранга - жилище кочевников севера. Вигвамы североамериканских индейцев. Чум жилище народов Севера имеет форму конуса.

H =4м, R =3м.

2.Русская изба.

a = 6м, b = 3м, c = 2,7м

3. Жилища народов кирди в Камеруне: R =2м, H =6м.

4.Снежный дом эскимосов.

К = 0,8

Изопериметрический коэффициент К всегда меньше 1 или равен ей.

Единственное тело, имеющее коэффициент, равный 1, - это шар

Жилье шарообразной формы радиусом R. Коэффициент комфортности близок к 1. Дом - сфера комфортен для жилья.

Дом - сфера. "Салекс" Чп Иващенко...

Заключение

Итак, в своей работе для достижения цели мною были проведены эксперименты, решены задачи и обоснована изопериметрическая проблема,

Среди геометрических фигур с равными периметрами наибольшую площадь имеет круг.

Из всех тел равного объема наименьшую поверхность имеет шар.

Капельки воды и мыльные пузыри не случайно имеют форму шара: силы поверхностного натяжения действуют так, чтобы уменьшать площадь поверхности. Характерно также, что кошки, когда холодно, спят, максимально сворачиваясь в клубок: так они уменьшают площадь поверхности тела, поскольку, чем меньше поверхность, тем меньше тепла они расходуют во внешнее пространство.

Ежедневно в нашей жизни нам встречаются задачи на нахождение наибольших или наименьших значений, потому что разумный человек непременно ищет такой путь, который поможет ему достигнуть наибольшей выгоды. Но при этом мы даже и не подозреваем, что в таком простом бытовом случае мы решаем изопериметрические задачи.

Изопериметрические задачи - это не только пример старинной математики, но и задачи, которые встречаются каждому из нас в реальной жизни.

Литература:

1.А.Б. Крыжановский «Изопериметры» М. - Л.,Физматлит, 1959 г.

2. Задачи открытого банка заданий по математике ФИПИ, 2010

3. С. Н . Олехин «Старинные занимательные задачи». Дрофа, Москва 2006.

4. Я. И. Перельман «Живая математика». Москва «Наука» 1978 г.

5. Спивак А.В. Тысяча и одна задача по математике: Кн. для учащихся 5-7 кл. -М.: Просвещение, 2010.

6. Тихомиров В. М. Рассказы о максимумах и минимумах. - 2-е изд., исправленное. - М.: МЦНМО, 2006.

7. Шарыгин Д. Миф о Дидоне и изопериметрическая задача. «Квант» №1, 1997г.

8. naukoved.ru

9. kvant.mccme.ru

10. goo.gl/PeqffB

11. philipok4.narod.ru/Tuser7/Starinnye_zadachi.pdf</<br>