Решение задач на работу в 9 классе

Задачи на работу

1. Два опе­ра­то­ра, ра­бо­тая вме­сте, могут на­брать текст га­зе­ты объ­яв­ле­ний за 8 ч. Если пер­вый опе­ра­тор будет ра­бо­тать 3 ч, а вто­рой 12 ч, то они вы­пол­нят толь­ко 75% всей ра­бо­ты. За какое время может на­брать весь текст каж­дый опе­ра­тор, ра­бо­тая от­дель­но?

Ре­ше­ние.

Пусть пер­вый опе­ра­тор может вы­пол­нить дан­ную ра­бо­ту за часов, а вто­рой за часов. За один час пер­вый опе­ра­тор вы­пол­ня­ет часть всей ра­бо­ты, а вто­рой . Со­ста­вим си­сте­му урав­не­ний:

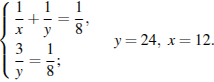
Ответ: пер­вый опе­ра­тор за 12 ч, вто­рой опе­ра­тор за 24 ч.

2. На из­го­тов­ле­ние 231 де­та­ли уче­ник тра­тит на 11 часов боль­ше, чем ма­стер на из­го­тов­ле­ние 462 таких же де­та­лей. Из­вест­но, что уче­ник за час де­ла­ет на 4 де­та­ли мень­ше, чем ма­стер. Сколь­ко де­та­лей в час де­ла­ет уче­ник?

Ре­ше­ние.

Пред­по­ло­жим, что уче­ник де­ла­ет де­та­лей в час. Тогда ма­стер де­ла­ет де­та­ли в час.
На из­го­тов­ле­ние 231 де­та­ли уче­ник по­тра­тит ч, а ма­стер тра­тит ч на из­го­тов­ле­ние 462 де­та­лей.
Со­ста­вим урав­не­ние по усло­вию за­да­чи:

.

Решим урав­не­ние:

.

Корни по­лу­чен­но­го квад­рат­но­го урав­не­ния: −28 и 3. От­бра­сы­вая от­ри­ца­тель­ный ко­рень, на­хо­дим, что уче­ник де­ла­ет в час 3 де­та­ли.

Ответ: 3.

3. Чтобы на­ка­чать в бак 117 л воды, тре­бу­ет­ся на 5 минут боль­ше вре­ме­ни, чем на то, чтобы вы­ка­чать из него 96 л воды. За одну ми­ну­ту можно вы­ка­чать на 3 л воды боль­ше, чем на­ка­чать. Сколь­ко лит­ров воды на­ка­чи­ва­ет­ся в бак за ми­ну­ту?

Ре­ше­ние.

Пусть за ми­ну­ту в бак на­ка­чи­ва­ет­ся лит­ров воды. Тогда за ми­ну­ту вы­ка­чи­ва­ет­ся л воды.
По усло­вию за­да­чи со­ста­вим урав­не­ние:

,

от­ку­да

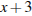
По­лу­ча­ем квад­рат­ное урав­не­ние

,

име­ю­щее корни: и .
От­бра­сы­вая от­ри­ца­тель­ный ко­рень, на­хо­дим, что за ми­ну­ту в бак на­ка­чи­ва­ет­ся 9 л воды.
Ответ: 9.

4. Дима и Саша вы­пол­ня­ют оди­на­ко­вый тест. Дима от­ве­ча­ет за час на 12 во­про­сов теста, а Саша - на 22. Они од­но­вре­мен­но на­ча­ли от­ве­чать на во­про­сы теста, и Дима за­кон­чил свой тест позже Саши на 75 минут. Сколь­ко во­про­сов со­дер­жит тест?

Ре­ше­ние.

Пусть x - ко­ли­че­ство во­про­сов теста через. Тогда по­лу­ча­ем:

от­ку­да на­хо­дим x = 33 .

Ответ: 33

5. Пер­вая труба про­пус­ка­ет на 2 литра воды в ми­ну­ту мень­ше, чем вто­рая. Сколь­ко лит­ров воды в ми­ну­ту про­пус­ка­ет вто­рая труба, если ре­зер­ву­ар объёмом 130 лит­ров она за­пол­ня­ет на 4 ми­ну­ты быст­рее, чем пер­вая труба за­пол­ня­ет ре­зер­ву­ар объёмом 136 лит­ров?

Ре­ше­ние.

Пусть вто­рая труба про­пус­ка­ет лит­ров воды в ми­ну­ту, тогда пер­вая труба про­пус­ка­ет литра в ми­ну­ту. Вто­рая труба за­пол­ня­ет ре­зер­ву­ар объёмом 130 лит­ров за минут. По­сколь­ку пер­вая труба за­пол­ня­ет ре­зер­ву­ар объёмом 136 лит­ров за минут, что по усло­вию за­да­чи на 4 ми­ну­ты боль­ше, чем по­лу­ча­ем урав­не­ние:

Решим урав­не­ние:

или

От­бра­сы­вая по­сто­рон­нее ре­ше­ние −6,5, по­лу­ча­ем, что вто­рая труба про­пус­ка­ет 10 лит­ров в ми­ну­ту.

Ответ: 10 лит­ров в ми­ну­ту.

6. Две трубы на­пол­ня­ют бас­сейн за 6 часов 18 минут, а одна пер­вая труба на­пол­ня­ет бас­сейн за 9 часов. За сколь­ко часов на­пол­ня­ет бас­сейн одна вто­рая труба?

Ре­ше­ние.

По усло­вию пер­вая труба за одну ми­ну­ту на­пол­ня­ет часть бас­сей­на, а две трубы вме­сте за одну ми­ну­ту на­пол­ня­ют часть бас­сей­на. Таким об­ра­зом, одна вто­рая труба за ми­ну­ту на­пол­ня­ет часть бас­сей­на, то есть она на­пол­ня­ет весь бас­сейн за 21 час.

Ответ: 21.

7. Три бри­га­ды из­го­то­ви­ли вме­сте 266 де­та­лей. Из­вест­но, что вто­рая бри­га­да из­го­то­ви­ла де­та­лей в 4 раза боль­ше, чем пер­вая и на 5 де­та­лей мень­ше, чем тре­тья. На сколь­ко де­та­лей боль­ше из­го­то­ви­ла тре­тья бри­га­да, чем пер­вая.

Ре­ше­ние.

Пусть - число де­та­лей, из­го­тов­лен­ных вто­рой бри­га­дой, тогда пер­вая бри­га­да из­го­то­ви­ла де­та­лей, а тре­тья - де­та­лей. Вме­сте три бри­гад из­го­то­ви­ли 266 де­та­лей, со­ста­вим урав­не­ние:

Вто­рая бри­га­да из­го­то­ви­ла 116 де­та­лей, сле­до­ва­тель­но, пер­вая бри­га­да из­го­то­ви­ла де­та­лей, а тре­тья - 121 де­таль. Таким об­ра­зом, тре­тья бри­га­да из­го­то­ви­ла на 121 − 29 = 92 де­та­ли боль­ше.

Ответ: 92.

8. Три бри­га­ды вме­сте из­го­то­ви­ли 114 син­хро­ни­за­то­ров пе­ре­дач. Из­вест­но, что вто­рая бри­га­да из­го­то­ви­ла син­хро­ни­за­то­ров в 3 раза боль­ше, чем пер­вая, и на 16 син­хро­ни­за­то­ров мень­ше, чем тре­тья. На сколь­ко син­хро­ни­за­то­ров пе­ре­дач боль­ше из­го­то­ви­ла тре­тья бри­га­да, чем пер­вая.

Ре­ше­ние.

Пусть пер­вая бри­га­да из­го­то­ви­ла x ра­ди­а­то­ров. Тогда вто­рая бри­га­да из­го­то­ви­ла 3x ра­ди­а­то­ров, а тре­тья 3x +16 ра­ди­а­то­ров. Из урав­не­ния 7x +16 =114 на­хо­дим, что пер­вая бри­га­да из­го­то­ви­ла 14 ра­ди­а­то­ров, а тре­тья 58 ра­ди­а­то­ров. Таким об­ра­зом, тре­тья бри­га­да из­го­то­ви­ла на 44 ра­ди­а­то­ра боль­ше, чем пер­вая.

Ответ: 44.