- Учителю
- Урок в 6 классе по теме 'Окружность. Длина окружности'
Урок в 6 классе по теме 'Окружность. Длина окружности'
Автор: Денисова Светлана Вячеславовна, учитель математики МБОУ СОШ с. Дуван, Республика Башкортостан, Дуванский район, с. Дуван, ул. Ленина, д. 77
Урок в 6 классе по теме «Окружность. Длина окружности.»
Тема: Окружность. Длина окружности.
Цель урока: изучить формулу длины окружности и показать её применение при решении задач.
Задачи урока:
Образовательные:
обеспечить усвоение учащимися формул по нахождению длины окружности;
познакомить с числом π;
отработать навыки применения данных формул при решении задач;
добиться усвоения учащимися понятий: длина окружности, число π.
Развивающие:
развивать навыки устного счёта;
развивать познавательный интерес учащихся в процессе ознакомления с историческим материалом;
Воспитательные:
воспитание мотивов учения, положительного отношения к знаниям;
воспитывать уважение и интерес к математике, умение видеть математические задачи в окружающем нас мире.
Ход урока.
-
Орг. Момент.
Психологический настрой на урок «СОТВОРИ СОЛНЦЕ СЕБЕ».
- Здравствуйте, ребята! В природе есть солнце. Оно всем светит и всех любит и греет. Давайте сотворим солнце себе. Закройте глаза, представьте в своем сердце маленькую звёздочку. Мысленно направляем к ней лучик, который несёт любовь. Звёздочка увеличивается. Направляем лучик, который несёт мир. Звёздочка опять увеличилась. Направляю Вам лучик с добром, звёздочка стала ещё больше. Я направляю к звёздочкам лучики, которые несут здоровье, радость, тепло, свет, нежность, ласку. Теперь звёздочка становится большой, как солнце. Оно несёт тепло всем-всем. (Руки в стороны перед собой).
-
Актуализация знаний.
Математика - наука древняя, интересная и полезная. Сегодня мы с вами убедимся в этом, и очень хочется, чтобы каждый из вас для себя сделал хотя бы небольшое, но открытие. А как сказал великий ученый, математик Лейбниц: "Кто хочет ограничиться настоящим, без знания прошлого, тот его никогда не поймёт…", то и нам с вами для успешной работы нужно повторить некоторые геометрические фигуры и понятия, вспомнить правила для округления десятичных дробей до различных разрядов, выполнения умножения и деления десятичных дробей.
-
Вычислите:
2 ∙ 3,1; 4 ∙ 3,12; 6 ∙ 6,24
-
Вставь пропущенное число:
…. : 5 = 2,5 18 ∙ …. = 5,4 …. ∙ 2 = 6,28
-
Округлить число:
а) до целого:
43,54 3,19
б) до сотых:
2,578 7,234
3.Постановка темы урока.
- Отгадайте загадку, и вы узнаете, о чём мы будем сегодня говорить
Если видишь солнце в небе, или чашку с молоком,
Видишь бублик или обруч, слышишь сказку с колобком,
В круглом зеркале увидел ты сейчас свою наружность.
И вдруг понял, что фигура называется окружность.
Так какая тема сегодняшнего урока? Правильно « Окружность. Длина окружности».
- Откройте тетради, запишите число и тему урока: «Окружность. Длина окружности.»
Какие мы поставим цели на урок? (1 повторить основные понятия темы «Окружность»; 2 вывести формулу для вычисления длины окружности; 3 учиться применять эту формулу при решении задач.)
Жили - были брат и сестра. Жили они дружно, да вот беда: были они очень похожи и ребята их часто путали. Брат был солидный, плотный, а сестра тонкая и прозрачная. У брата было много друзей: диски, тарелки, монетки, блинчики. А у сестры друзей не меньше: кольца, браслеты, обручи и даже бублики… И всё у них было общее. Догадались, кто это брат и сестра? (Круг и окружность)
-
Изучение нового материала.
-
Работа по чертежу.
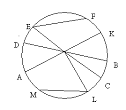
- Что такое окружность, круг?
- Назовите центр окружности.
- Чем является отрезок АК?
- Есть ли на чертеже еще диаметры?
- Чем является отрезок ОВ?
- Есть ли на чертеже еще радиусы? Сколько радиусов можно провести?
- Как называется отрезок ML?
- Есть ли на чертеже еще хорды?
- Можно ли измерить длину хорды, радиуса?
- С помощью какого измерительного прибора это можно сделать? Какими единицами измерения будет выражен результат?
2) Создание проблемной ситуации.
Можно ли измерить длину окружности? С помощью какого измерительного прибора это можно сделать? Как это можно сделать? (Возможные ответы: с помощью нитки, веревки и т.п.)
3)Практическая работа.
- Ребята, еще в далёкой древности было установлено, что есть зависимость между длиной окружности и её диаметром.
Давайте же и мы попробуем её установить, для этого вы выполните практическую работу, в которой будете использовать способ измерения длины окружности, предложенный вами, но для удобства будете пользоваться ниткой. У вас на столах лежат различные круги и как вы говорили, что граница круга - это окружность, то длины окружностей их ограничивающие различны. Работать вы будете парами. Вы берете модель, обвязываете её ниткой, распрямляете и измеряете длину нитки (т.е. измерьте длину окружности). Результат занесем в таблицу. Затем линейкой измерьте диаметр и внесите значение в таблицу.
А теперь внимательно посмотрите на последнюю колонку и сделайте вывод: во сколько раз длина окружности больше диаметра. (дети выполняют работу)
Проверка работы. Что у нас получилось? Посмотрите, ребята, какие окружности у вас были (разные), а отношения длин окружностей к их диаметрам какими получились? (получились одинаковые). Это характерно для всех окружностей? Какой вывод можно сделать? Формулирование вывода учащимися.(Какими бы различными ни были окружности, отношения их длин к диаметрам будут постоянно одинаковыми. Длина больше диаметра приблизительно в 3 раза.)
Сейчас мы с вами пришли к такому же выводу, что и наши далекие предки много веков назад. Они заметили, что для того, чтобы сплести корзину нужной ширины, или, как мы теперь говорим диаметра, нужно было брать прутья примерно в три раза длиннее. Это было первое открытие, с тех пор прошло немало веков, прежде чем ученые доказали, что результат деления длины окружности на её диаметр постоянен и выражается не натуральным числом. А каким же?
Если вы, ребята, округлили ваш результат, то ваш товарищ, выполнял
следующее задание: попробовал выполнить деление С=22 на d=7 до конца. И что же у тебя получилось, ученик записывает свой результат. Да, действительно, получается бесконечная десятичная дробь. К такому выводу пришел древнегреческий ученый Архимед.
4) Историческая справка.
В 1706 году английский математик Уильямс Джонс для него ввел специальное обозначение ![]() =3,1415926.. - это первая буква слова "периферия", в переводе с греческого "окружность". Необычность и удивительность этого числа в том, что его можно вычислять бесконечно и у него будет бесконечно знаков после запятой. Это, однако, не удерживает математиков от попыток вычислить как можно больше десятичных знаков числа пи. О нём говорят, как о неуловимом числе. Вот как, например, выглядит значение с семью знаками после запятой. Для запоминания этих знаков есть стишок: Нужно только постараться
=3,1415926.. - это первая буква слова "периферия", в переводе с греческого "окружность". Необычность и удивительность этого числа в том, что его можно вычислять бесконечно и у него будет бесконечно знаков после запятой. Это, однако, не удерживает математиков от попыток вычислить как можно больше десятичных знаков числа пи. О нём говорят, как о неуловимом числе. Вот как, например, выглядит значение с семью знаками после запятой. Для запоминания этих знаков есть стишок: Нужно только постараться
И запомнить все как есть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть.
Для обычных вычислений с числом p вполне достаточно запомнить два знака после запятой (3,14). Число π используется не только в математике, но и в физике. С этим предметом вам предстоит познакомиться на следующий год.
4) Вывод формулы.
Вернемся к нашей проблеме нахождения длины окружности. А сможете ли с помощью всё той же нитки найти длину любой окружности? Например, большой трубы? Конечно же нет. Но зная, что С/d = π, выразим длину окружности С= π d.
Итак, длина окружности равна произведению диаметра на число π. А так как d=2r, то С =2 π r. (формулы записываются учителем на доске)
- Запишите формулы в тетрадь.
Физкультминутка.
А теперь ребята встали
Быстро руки вверх подняли
В стороны, вперед, назад.
Повернулись влево, вправо
Тихо сели, вновь за дело.
-
Закрепление изученного.
Задача1. А сейчас мы поработаем по нашим формулам, устно выполним задания.
-
Диаметр равен 10м (2см). π ≈ 3,14. Вычислите длину окружности.
-
Радиус равен 3км (15м). π ≈ 3. Вычислите длину окружности.
-
Длина окружности равна 33,3 см (18 км). π ≈ 3. Вычислите диаметр.
- А как вы думаете, зачем нам нужно знать длину окружности? Ученики высказывают свои предположения, приходим к выводу, что бывают ситуации, когда необходимо знать длину окружности.
Задача 2. Найдите, какой длины бордюр потребуется для ограждения клумбы, имеющей форму круга с диаметром, равным 4м. ( С = 3,14 * 4 = 12,56м)
Задача 3. Диаметр Луны приблизительно равен 3476 км. Найдите длину лунного экватора ( с точностью до сотен километров). (С = 3,14 *3476 ≈10914,64 ≈10900км)
Тест первичного закрепления.
Учащиеся выполняют тест, обводя правильный ответ кружком. Затем обмениваются работой с соседом по парте, при этом открываются правильные ответы, и выставляют оценки: - без ошибок-5; - с одной ошибкой-4)
ТЕСТ
-
Отрезок, соединяющий две точки окружности и проходящий через центр.
А) радиус; Б) сторона; В) хорда; Г) диаметр.
-
Число π равно
А) 3,14; Б) 1,34; В) 3,91; Г) 4,13.
-
Формула длины окружности
А) С=πr Б) С=πd В) C=2πd Г) C=2r
-
Чему равен диаметр окружности, радиус которой 3,8 см?
А) 6,28 Б) 1,57 В) 7,6 Г) 3,14
6. Домашнее задание.
Поскольку математика тесно связана с жизнью, с окружающей нас средой, в чем вы сегодня убедились, то и задание у вас будет творческое. Может, вы, увидите окружность в колесе, может в цирке, а у кого-то есть велосипед, у мамы на кухне кастрюли, кто-то крутит обруч, а кто-то любит искать города на глобусе. Придумайте и составьте задачу по теме «Длина окружности» и сделайте красочный рисунок к задаче.
Или № 649, 654.
7.Подведение итогов.
А сейчас давайте вспомним, что сегодня на уроке мы:
-
Повторили… (Что такое окружность, радиус, диаметр, как они связаны друг с другом).
-
Узнали… ( Формулы, по которым вычисляется длина окружности).
-
Закрепили… (Научились применять эти формулы при решении задач).
8. Рефлексия.
- Что на уроке понравилось?
- Что не удалось?
- Где в жизни пригодятся знания по данной теме?
- Какие цели мы поставим на следующий урок?