- Учителю
- По математике на тему Кеңістіктегі тікбұрышты координаталар жүйесі.
По математике на тему Кеңістіктегі тікбұрышты координаталар жүйесі.
Жамбыл облысы
Меркі ауданы
Ойтал ауылы
№12 Қ.Сарымолдаев атындағы орта мектеп
Математика пәнінің мұғалңмң: Саркулова Анар Кыргызбековна
Күні: 11.03.2011жыл Пәні: Геометрия Сынып:10
Сабақтың тақырыбы: Кеңістіктегі тікбұрышты координаталар жүйесі.
Сабақтың мақсаты:
-
Білімділік. Оқушыларға кеңістіктегі тікбұрышті координатлар жүйесі түсінігімен таныстыру.
-
Дамытушылық. Оқушыларды кооординаталары бойынша нүктені салуды, тікбұрышты координаталар жүйесінің осьтеріндегі және жазықтықтарындағы нүктелердің координаталарын анықтай білуге дағдыландыру.
-
Тәрбиелік. Оқушыларды ұйымшылдыққа, ұқыптылыққа, дәлдікке тәрбиелеу, өз біліміне жауапкершілікпен қарауға дағдыландыру.
Сабақ типі: Жаңа сабақ
Сабақ түрі: Аралас сабақ
Сабақ әдісі: Түсіндіру, есептер шығару.
Сабақтың көрнекілігі: семантикалық карта, бағалау парағы, есептер жазылған плакаттар.
Сабақтың жоспары: І. Ұйымдастыру кезеңі
ІІ. Үй тапсырмасын тексеру
ІІІ. Өткен сабаққа шолу
ІV. Жаңа сабақ
V. Бекіту
VІ. Қорытындылау
VІІ. Үйге тапсырма беру
VІІІ. Бағалау
Сабақ барысы:
І. Ұйымдастыру кезеңі:
1. Сәлемдесу
2. Оқушыларды түгелдеу
3. Зейіндерін сабаққа аудару
ІІ. Үй тапсырмасын тексеру
Қайталау сұрақтары.
-
Жазықтық пен түзудің арасындағы бұрыш дегеніміз не?
-
Түзу мен жазықтықтың арақашықтығы дегеніміз не?
-
Түзу мен жазықтық қалай орналасуы мүмкін?
ІІІ. Өткен сабаққа шолу
Сөзжұмбақ «Кеңістік» шешу.
-
Бір ұшы жазықтықта жататын және жазықтыққа перпендикуляр болмайтын кесінді
-
Кесіндінің жазықтықтағы ұшы мен көлбеудің табанын қосатын кесінді
-
900<α<1800 қандай бұрыш?
-
Екі ұшы нүктемен шектелген сәуле
-
Кеңістікте бір жазықтықта жатпайтын түзулер
-
Кеңістіктегі фигураларды зерттейтін ғылым
-
Перпендикуляр түзулер арасындағы бұрыш қандай?
-
Барлық қабырғалары тең параллелепипед
ІV. Жаңа сабақ
О нүктесінде қиылысатын өзара перпендикуляр x, y, z
координаталық түзулері координаталық осьтер, ал О(0; 0; 0) нүктесін
координаталардың бас нүктесі дейміз. Әрбір координаталық осьті О
нүктесі оң және теріс жарты оське бөледі. Координаталық осьтердің
әрбір жұбы - x пен y, x пен z, y пен z - координаталық
жазықтықтарды анықтайды, олар былай белгіленеді:Оху, Оуz, Оzх.
Координаталық жазықтықтар кеңістікті сегіз бөлікке бөледі. Ол
бөліктерді октанталар деп атайды.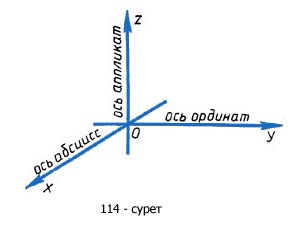
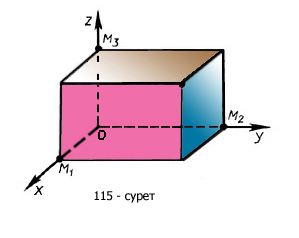
Осындай координаталық жүйенің көмегімен кеңістіктің әрбір нүктесіне нақты сандардың реттелген үштігін немесе керісінше әрбір үш санға жалғыз нүктені сәйкес қоюға болады. Кеңістікте М нүктесі берілсін. Нүктеден yz, zx, x y жазықтықтарына ММx, ММy, ММz перпендикулярын түсіреміз. Осы перпендикулярлардың ұзындықтарын сәйкес таңбаларымен алып, М нүктесінің координаталары деп атаймыз да М(a, b, c) деп белгілейміз.
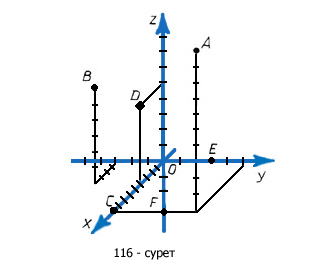
М нүктесінің координаталары М әрпінен кейін жай жақшалардың ішіне жазылып көрсетіледі: М(х; у; z), мұнда бірінші абсцисса, екінші ордината, үшінші аппликата жазылады. 116-суретте А(9; 5; 10), B(4; -3; 6), С(9; 0; 0), D(4; 0; 5), Е(0; 8; 0), F(0; 0; -3) нүктелері кескінделген.
V. Бекіту
Есептер шығару
№1. Координаталары бойынша А(3;1; 2), B(-1; 4; 0), С(0; 0; 53), D(2; 51; 0) нүктелерін салыңдар.
№2. А(1; 7; 3), B(3; 0; 0), С(1; 2; 0), D(0; 5; 1) нүктелдері берілген. Осы нүктелердің қайсысы 1) xy жазықтығында; 2) yz жазықтығында; 3) x осінде жатады?
№3. М(9; 5; 10) нүктесі берілген. Осы нүктеден координаталық осьтерге және координаталық жазықтықтарға түсірілген перпендикулярдың табандарының ұзындығын табыңдар.
№4. Барілген А(-4; 0; 0), B(5; -3; 0), С(0; 2; 0), D(4; -6; 0), Е(0; 0; -10), F(0; 9; -7) нүктелерінің ішінен а) Оx осінде; ә) Оy осінде; б) Оxy жазықтығында; в) Оyz жазықтығында жататын нүктелерді анықтаңдар
№5 берілген М(0; 0; 5), К(0; -1; -2) нүктелеріне а) Оxy жазықтығына қарағанда; ә) Оy осіне қарағанда симметриялы нүктелердің координаталарын табыңдар.
VІ. Қорытындылау
Кеңістіктегі тікбұрышты координаталар жүйесінің жазықтықтағы тікбұрышты координаталар жүйесінен айырмашылығы неде?
VІІ. Үйге тапсырма беру
§19. № 5 (69 бет)
VІІІ. Бағалау