Конспект урока по теме

Биквадратные уравнения

Алгебра 8 класс

Учитель математики

МАОУ «Ангарский лицей №1»

Никифорова С.В.

Цель - создать алгоритм решения биквадратного уравнения.

Задачи

1. Познакомиться с новым видом уравнений и способом его решения.

2. Развивать умение анализировать, сравнивать, обобщать, применять старые знания, умения и навыки в новой ситуации, развивать внимание и память.

3. Воспитывать чувство товарищества, уважение мнения товарищей.

Оборудование:

1. Доска, мел; интерактивная доска (при отсутствии доски - карточки с примерами уравнений разных видов).

2. Карточки для составления формулы корней квадратного уравнения.

3. Карточки с заданиями для групп.

4. Карточки с домашним заданием.

Литература:

1. А.Г. Мордкович Алгебра 8 класс. Учебник для общеобразовательных учреждений - М.: Мнемозина, 2012;

2. А.Г. Мордкович, Т.Н. Мишустина, Е.Е. Тульчинская. Алгебра 8 класс. Задачник для общеобразовательных учреждений - М.: Мнемозина, 2012;

3. Л.А. Александрова Алгебра 8 класс: Самостоятельные работы для общеобразовательных учреждений. - М.: Мнемозина, 2012;

Распределение времени:

Время

Организационный

2 минуты

Подготовка к сообщению темы урока

7 минут

Повторение ранее изученного материала

9 минут

Знакомство с новым материалом

10 минут

Составление алгоритма решения нового уравнения

7 минут

Тренировочное упражнение

6 минут

Домашнее задание и подведение итогов урока

4 минуты

Распределение по группам:

Учащиеся со средними математическими способностями

3 группа:

Учащиеся с хорошими математическими способностями

Ход урока.

Организационный этап.

Учитель приветствует учеников, настраивает их на работу, желает творческих успехов в изучении новой темы.

Подготовка к сообщению новой темы.

Чем же мы будем сегодня заниматься на уроке? Чтобы получить ответ на этот вопрос, вам предстоит разгадать кроссворд.

1. Последняя буква алфавита.

2. Столица Италии.

3. У кого днём один глаз, а ночью много?

4. Самая плохая оценка (7 букв).

5. На пяти проводах отдыхает стая птах.

6. Фамилия знаменитого французского учёного, установившего зависимости между корнями уравнения любой степени и его коэффициентами.

7. Домашний бассейн для рыб.

8. Республика, в которой мы живём.

9. Орган слуха.

Ответы: 1. Я. 2. Рим. 3. Ночь. 4. Единица. 5. Ноты. 6. Виет. 7. Аквариум. 8. Россия. 9. Ухо.

А теперь буквы выделенного столбика расположите снизу-вверх и получите ключевое слово. Что получилось? Верно, УРАВНЕНИЕ.

Итак, чем же мы будем заниматься сегодня на уроке? - Решать уравнения!

Повторение ранее изученного материала.

Мы с вами уже давно решаем уравнения. Давайте вспомним, с какими видами уравнений мы уже встречались?

1. Линейные.

2. Квадратные.

3. Дробно-рациональные.

4. Иррациональные.

А квадратные уравнения имеют один и тот же вид, или их можно разбить на несколько групп?

Да, квадратные уравнения бывают нескольких видов:

1. Полные квадратные уравнения.

2. Неполные квадратные уравнения.

3. Приведённые квадратные уравнения.

А теперь внимательно посмотрите на эти уравнения:

1. .

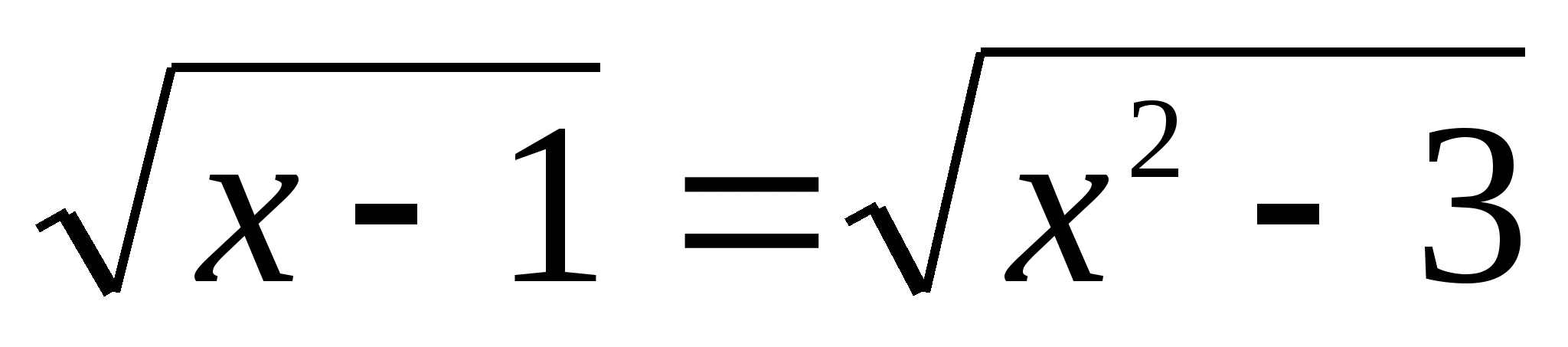2. 2.

3. .

4. .

5. .

6. .

7. .

8. .

9. .

10. .

11. .

12. .

13. .

14. .

15. .

16. .

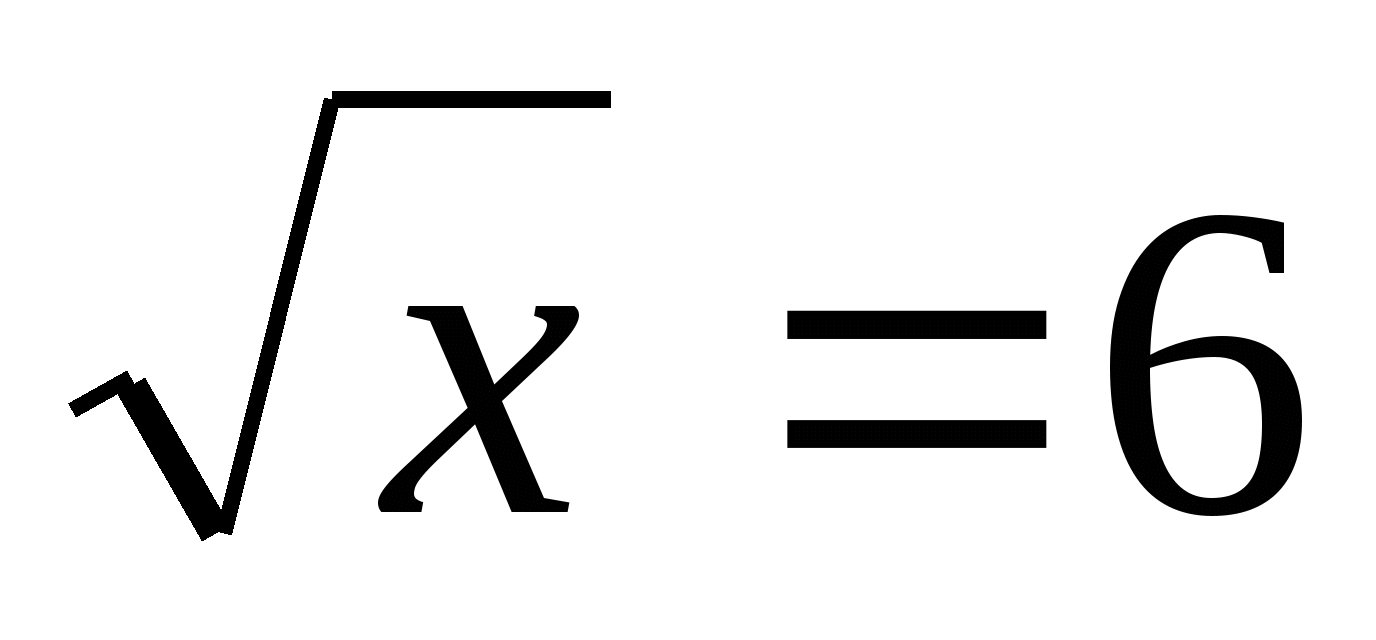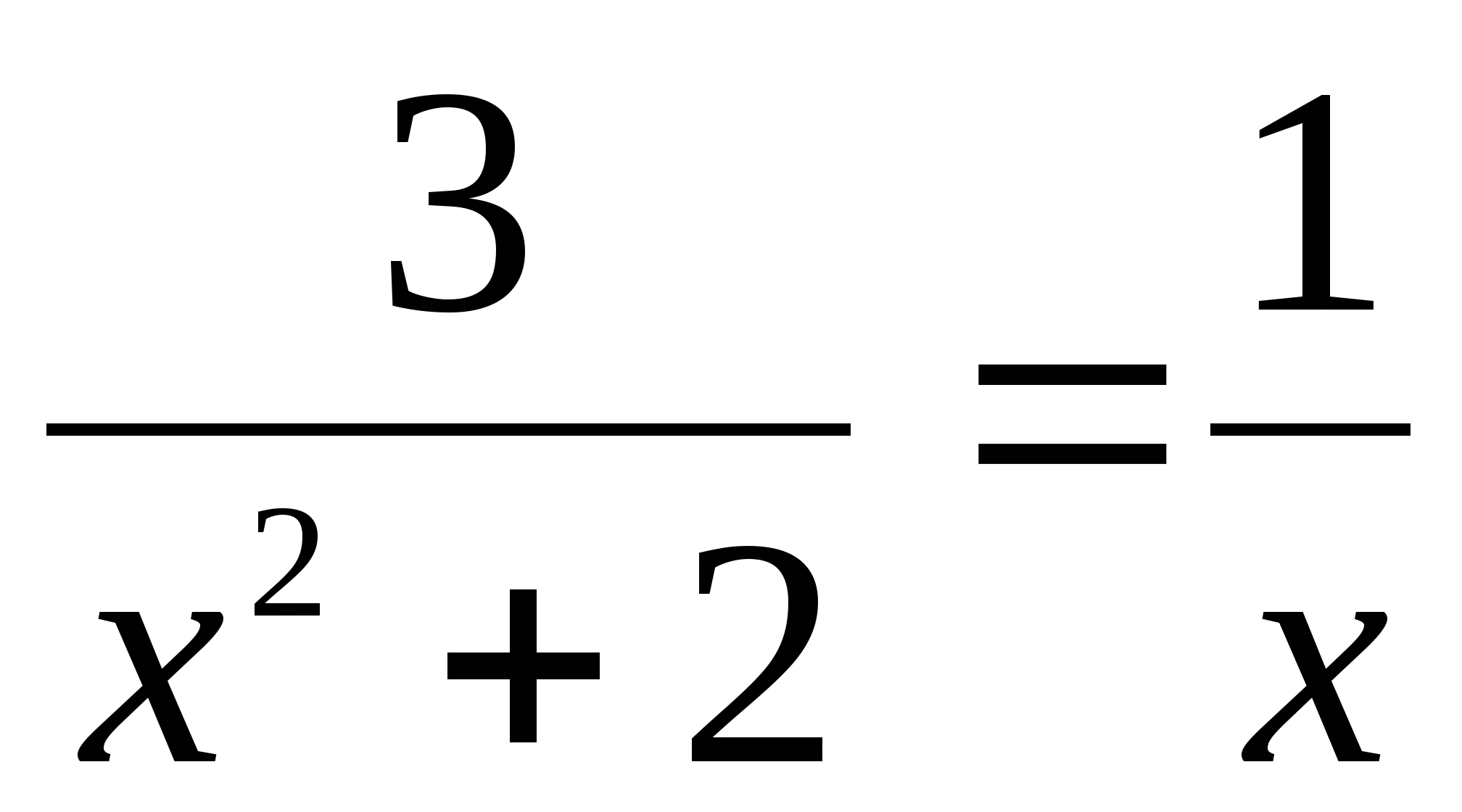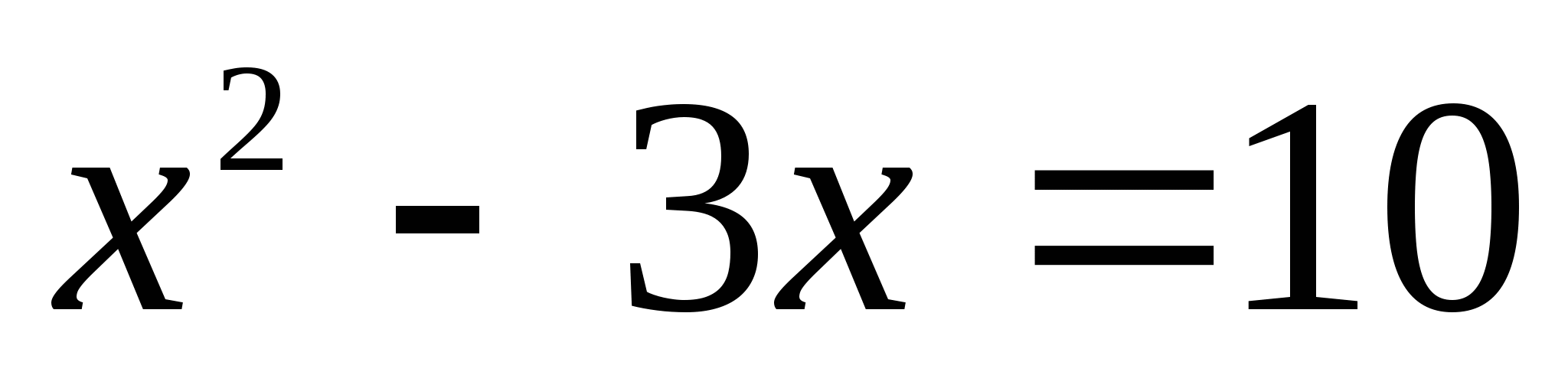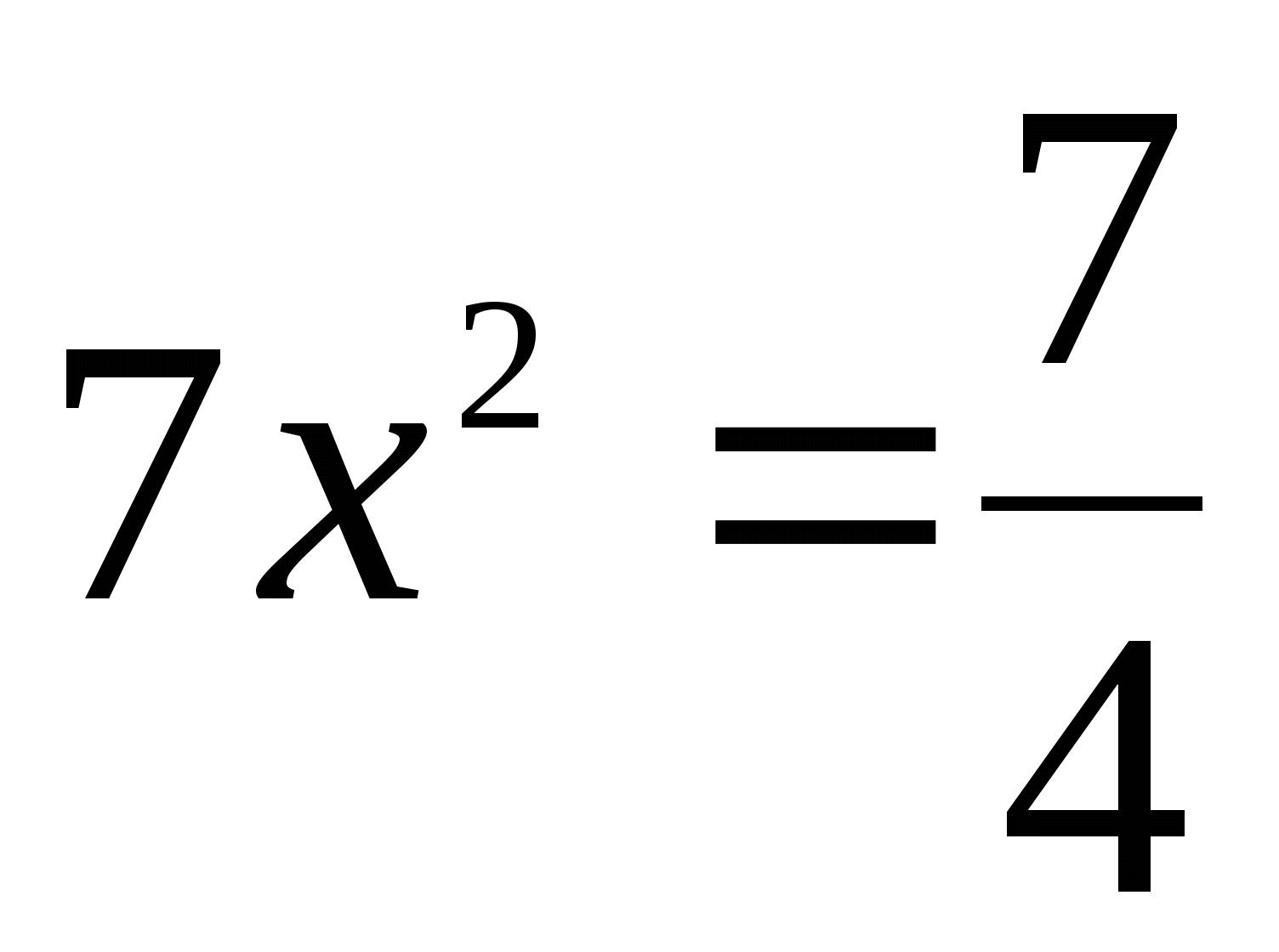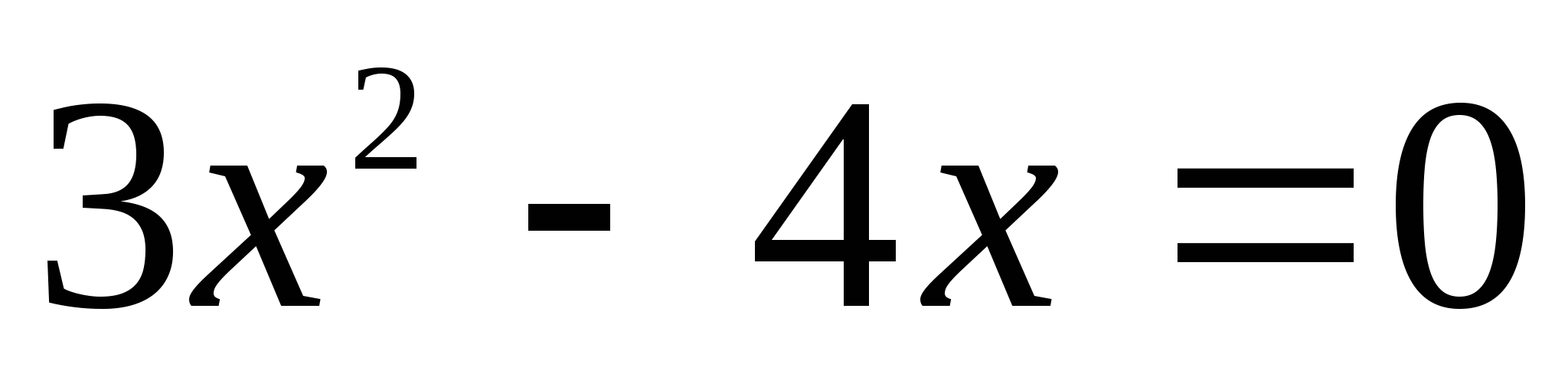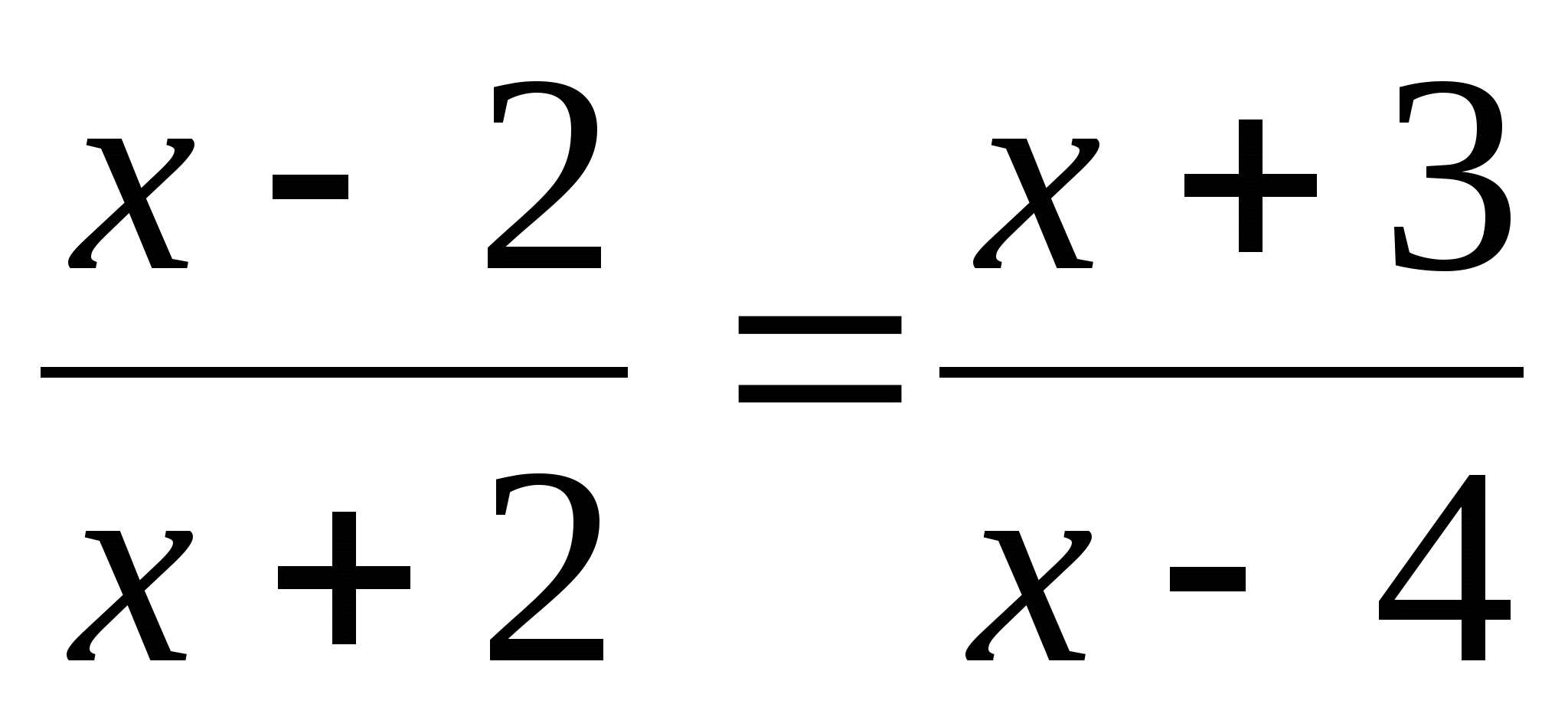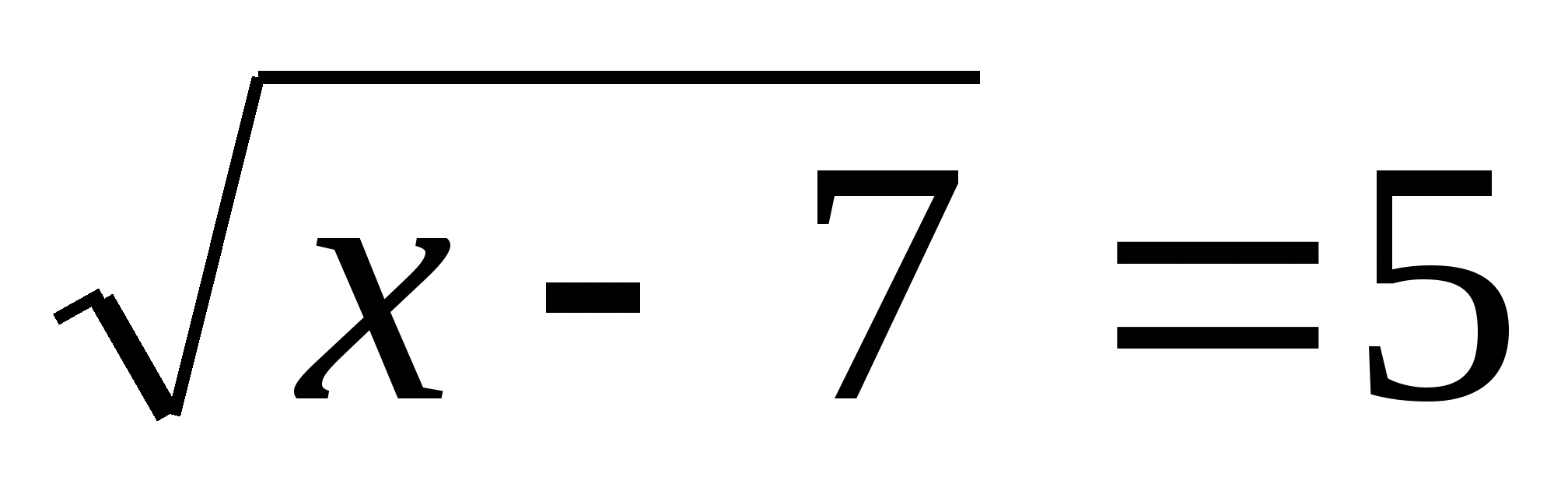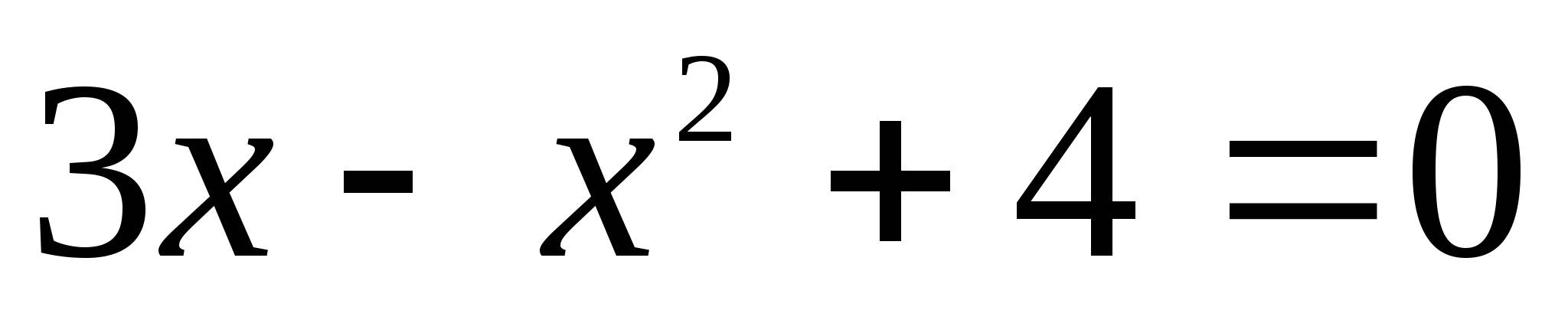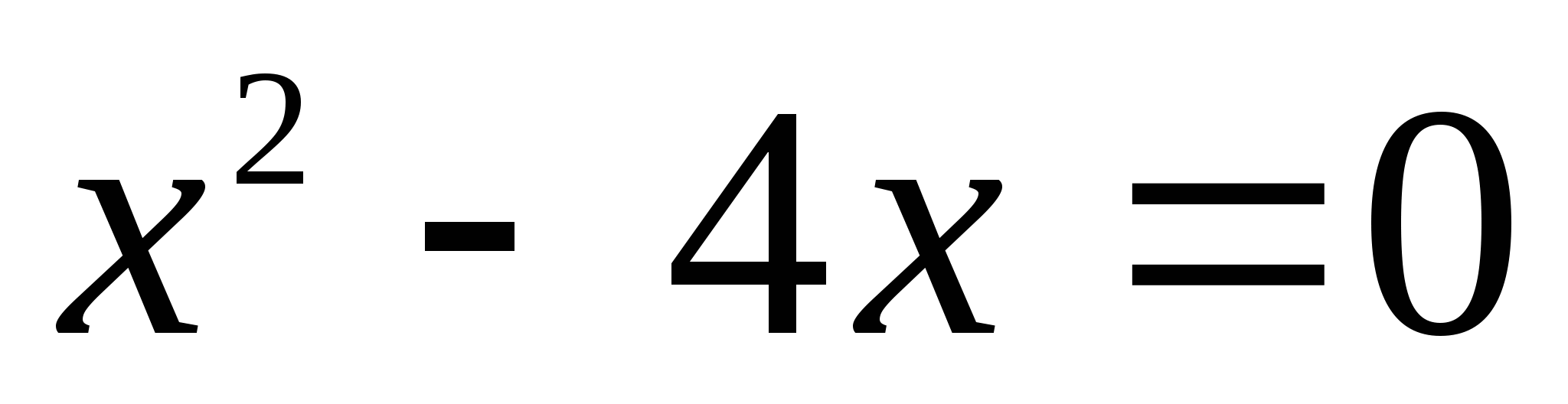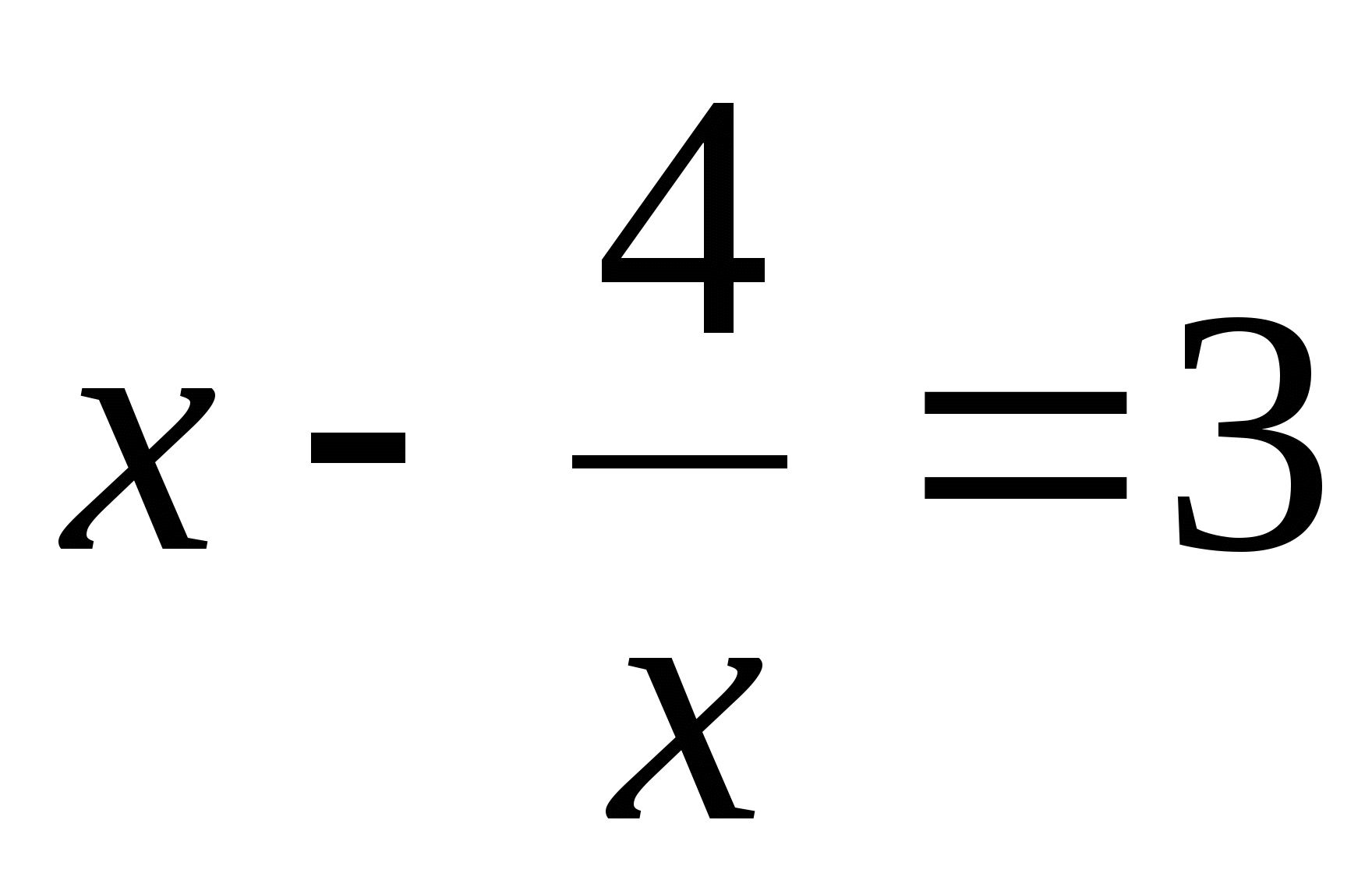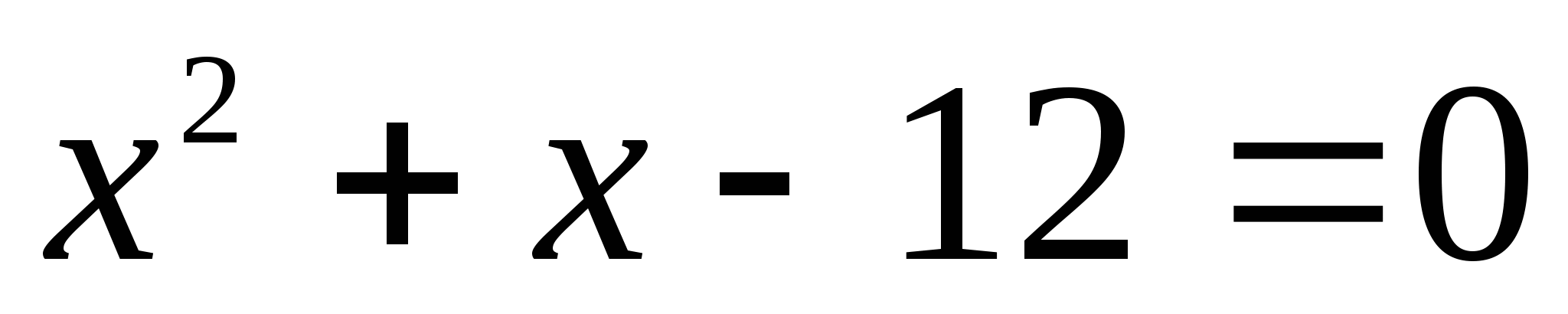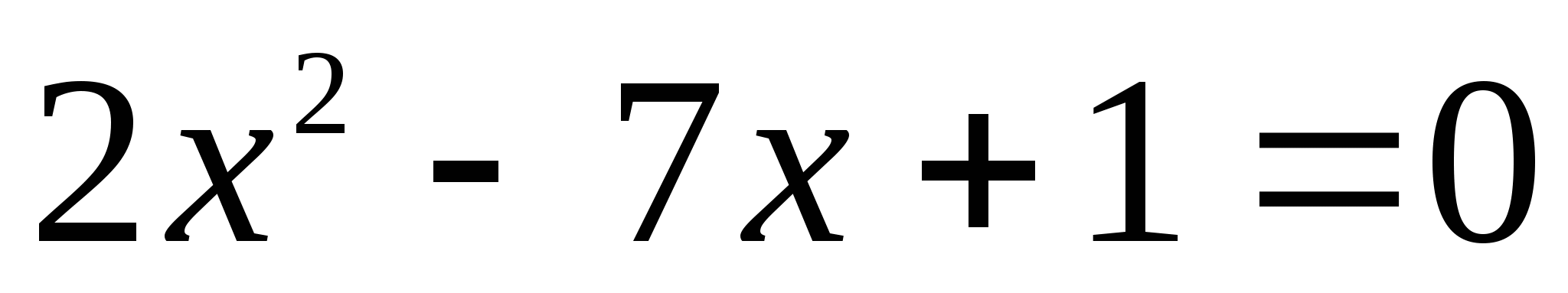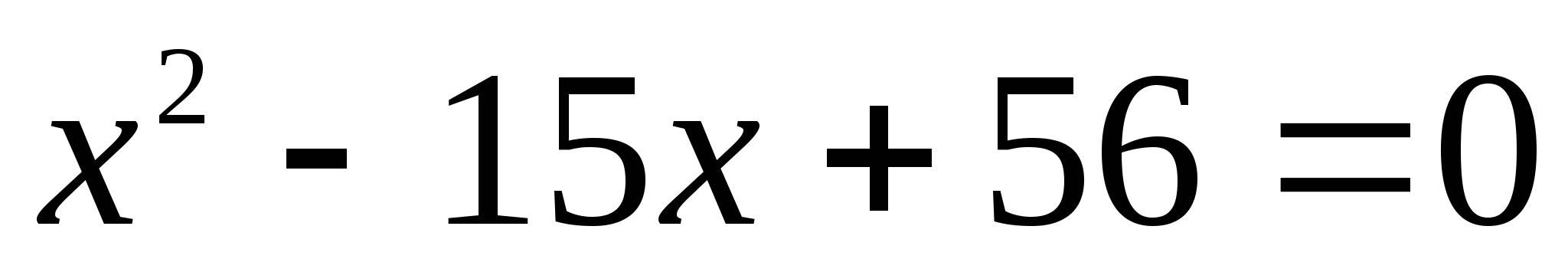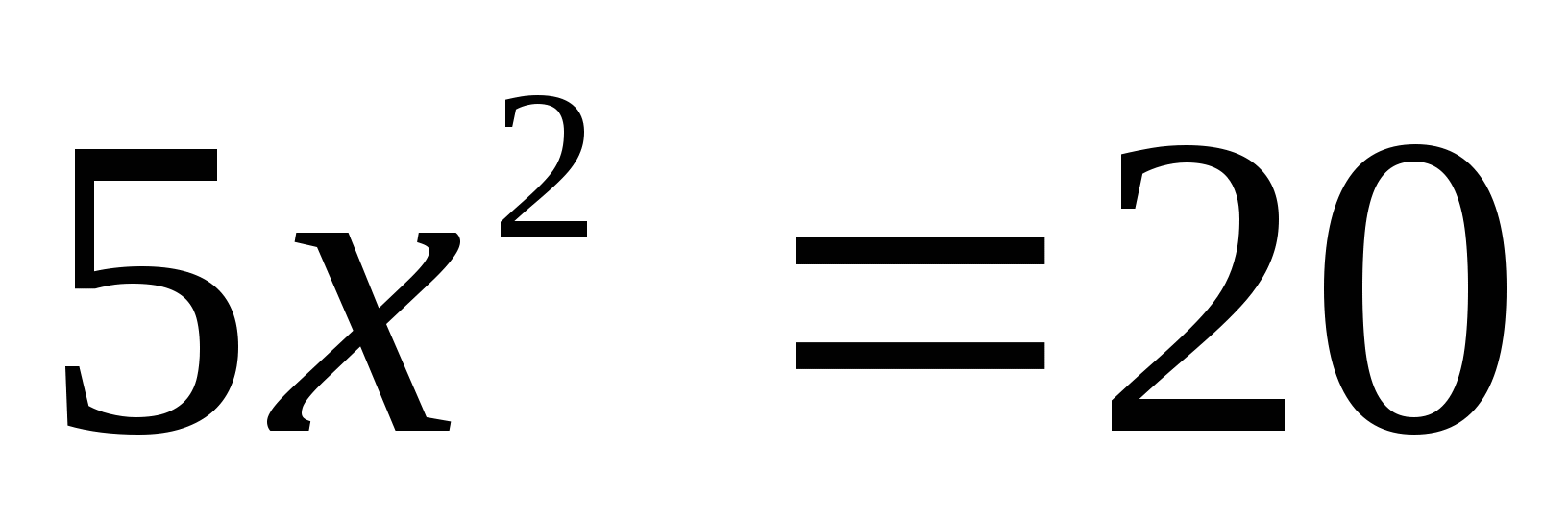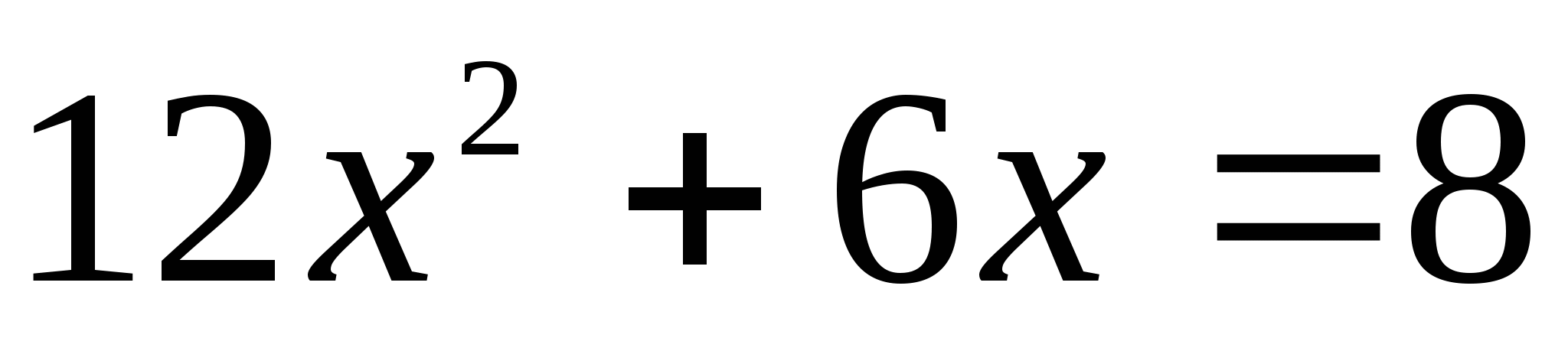Эти 16 уравнений нужно рассортировать по группам, учитывая их виды. На обдумывание даётся 2 минуты. После обсуждения по одному представителю от каждой команды выходят к доске и прикрепляют в ячейки соответствующие уравнения, (вид уравнения выбирают команды сами, начиная с первой).

Какое же из всех эти уравнений является основным? - Полное квадратное!

Давайте вспомним общий вид полного квадратного уравнения.

Один человек (по желанию) выходит к доске и восстанавливает формулу общего вида квадратного уравнения, другой - формулу для нахождения корней квадратного уравнения.

Знакомство с новым материалом.

Перед вами решение квадратного уравнения:

Ответ:

Посмотрите ещё раз внимательно на само уравнение и запомните его. (Уравнение закрывается). А теперь посмотрите на такое уравнение:

Похоже ли это уравнение на предыдущее? Есть ли отличия и в чём? А сможем ли мы решить это уравнение? Что нам мешает это сделать?

Прежде, чем приступать к решению, давайте, сравним пары:

Что общего у этих пар?

Вернёмся к нашему уравнению. Нельзя ли свести наше уравнение к старому? Как это сделать?

Заменим на , а на

Тогда уравнение примет вид:

Это уравнение мы можем решить, при этом получим корни:

Мы нашли значения , а первоначально ведь дана была переменная . Что же нам делать дальше?

Вернёмся к старой переменной и при этом получим два квадратных уравнения относительно переменной :

Ответ:

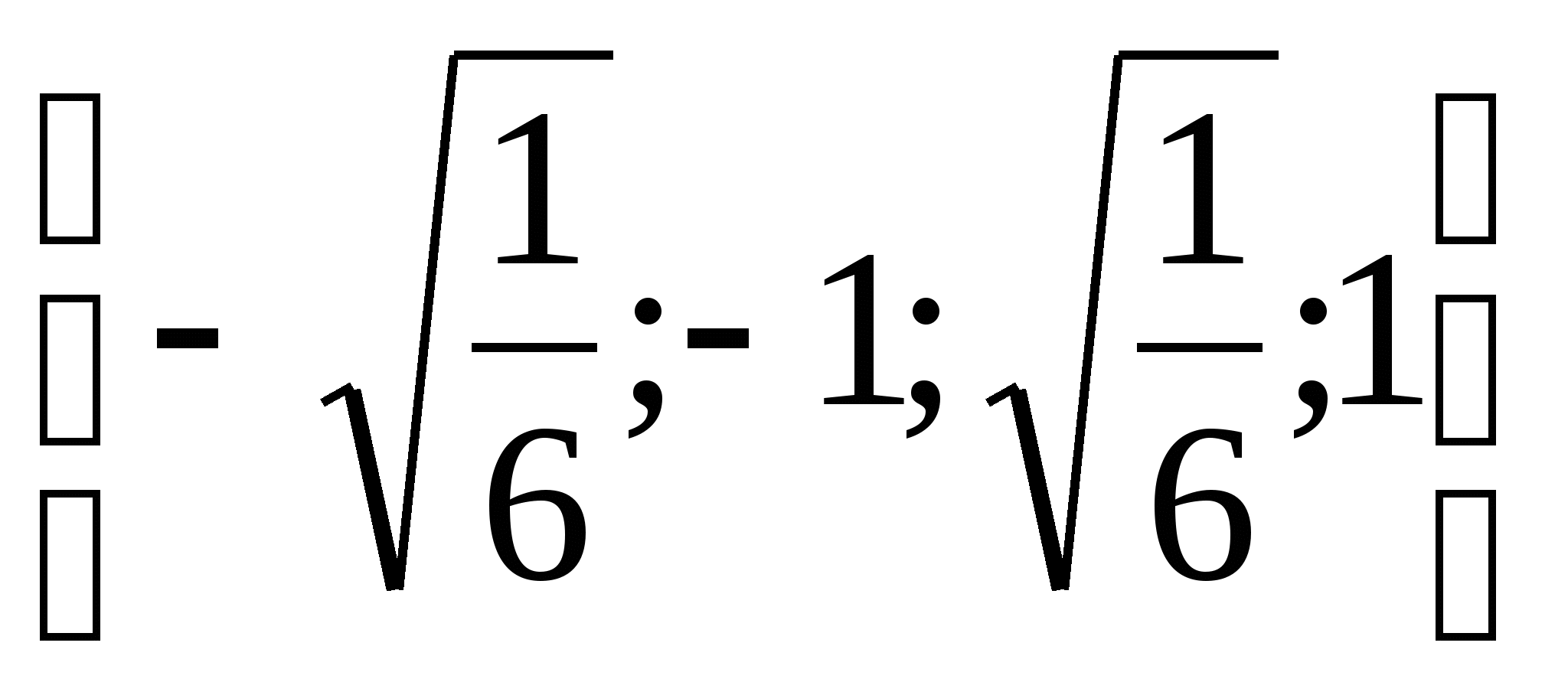
Мы решили с вами новое уравнение, которое носит название БИКВАДРАТНОЕ. Приставка «БИ» означает два, т.е. «дважды квадратное».

Определение. Уравнение вида называется биквадратным.

Составление алгоритма решения уравнения.

Давайте, восстановим наше решение по шагам:

1. Выделили элементы уравнения.

2. Установили общие свойства у этих элементов.

3. Выполнили подстановку.

4. Составили уравнение относительно новой переменной.

5. Решили квадратное уравнение.

6. Вернулись к старой переменной и получили 2 квадратных уравнения относительно переменной .

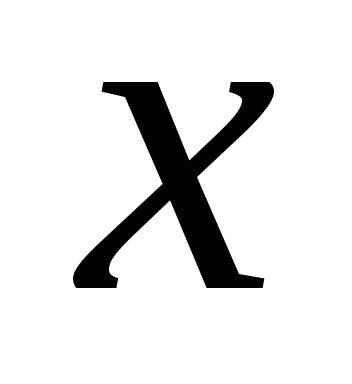7. Решили уравнения.

8. Записали ответ.

Тренировочное упражнение.

А теперь, пользуясь алгоритмом, восстановите решение уравнения.

Первая группа собирает мозаику по решённому уравнению, затем ученики решение записывают в тетрадь.

Вторая группа восстанавливает решение самостоятельно и сверяется с доской.

Третья группа решает аналогичные уравнения.

Домашнее задание.

1. Учебник: стр.150 - 153, разобрать и записать в тетрадь решения примеров 4 и 5.

2. Задачник: стр.169, №№ 26.15(аб), 26.16(аб), 26.16 (аб).

3. № 26.26(а), 26.27(а) - для учащихся с хорошими математическими способностями.

Итог урока.

Что нового вы сегодня узнали на уроке? Всё ли было понятно? В чём были трудности? Над чем надо продолжить работу?

Выставление оценок за работу на уроке.