Методическая разработка урока на тему Системы линейных уравнений с параметрами

Методическая разработка

Тема: « Решение систем линейных уравнений с параметром»

Объяснение теоретического материала.





Определение. Системой линейных уравнений с двумя переменными называется два линейных уравнения, рассматриваемых совместно:

Решениями системы линейных уравнений называются такие пары чисел , которые являются

решениями одновременно и первого, и второго уравнения системы.





Пусть числа отличны от нуля.



Если , то система имеет единственное решение.



Если , то система не имеет решений.



Если , то система имеет бесконечно много решений.



Если с_1, с₂ равны нулю, то система называется однородной и всегда имеет решение (0 ; 0). Если однородная система имеет нулевое решение (x₀; y₀), значит, она имеет бесконечное множество решений (kx₀; ky₀).





Пример 1. При каких значениях параметра a система

а) имеет бесконечное множество решений;



б) имеет единственное решение?





Решение. Данная система уравнений является линейной, причем коэффициенты первого уравнения

отличны от нуля.



а) Система имеет бесконечное множество решений, если а = 4.



б) Система имеет единственное решение, если а4



Обратить внимание на то, что уравнения поменяли местами, так как число а неопределенно.

В нашем случае а=0 является решением в случае б), чтобы не было недоумений с делением на нуль,

лучше вторым считать то уравнение, в котором все коэффициенты определены и не равны нулю.





Ответ: а) если а = 4, то система имеет бесконечное множество решений;

б) если а4, то решение единственное.

Пример 2. Решите систему уравнений:

Решение. Данная система уравнений является линейной.



а) Система имеет единственное решение, если , то есть m.



Решим систему при m:

1-(m+1) y = n-2y;



2y-(m+1) y = n-1;



y (1-m) = n-1;



, где m1.



Найдем х, воспользовавшись любым уравнением системы:







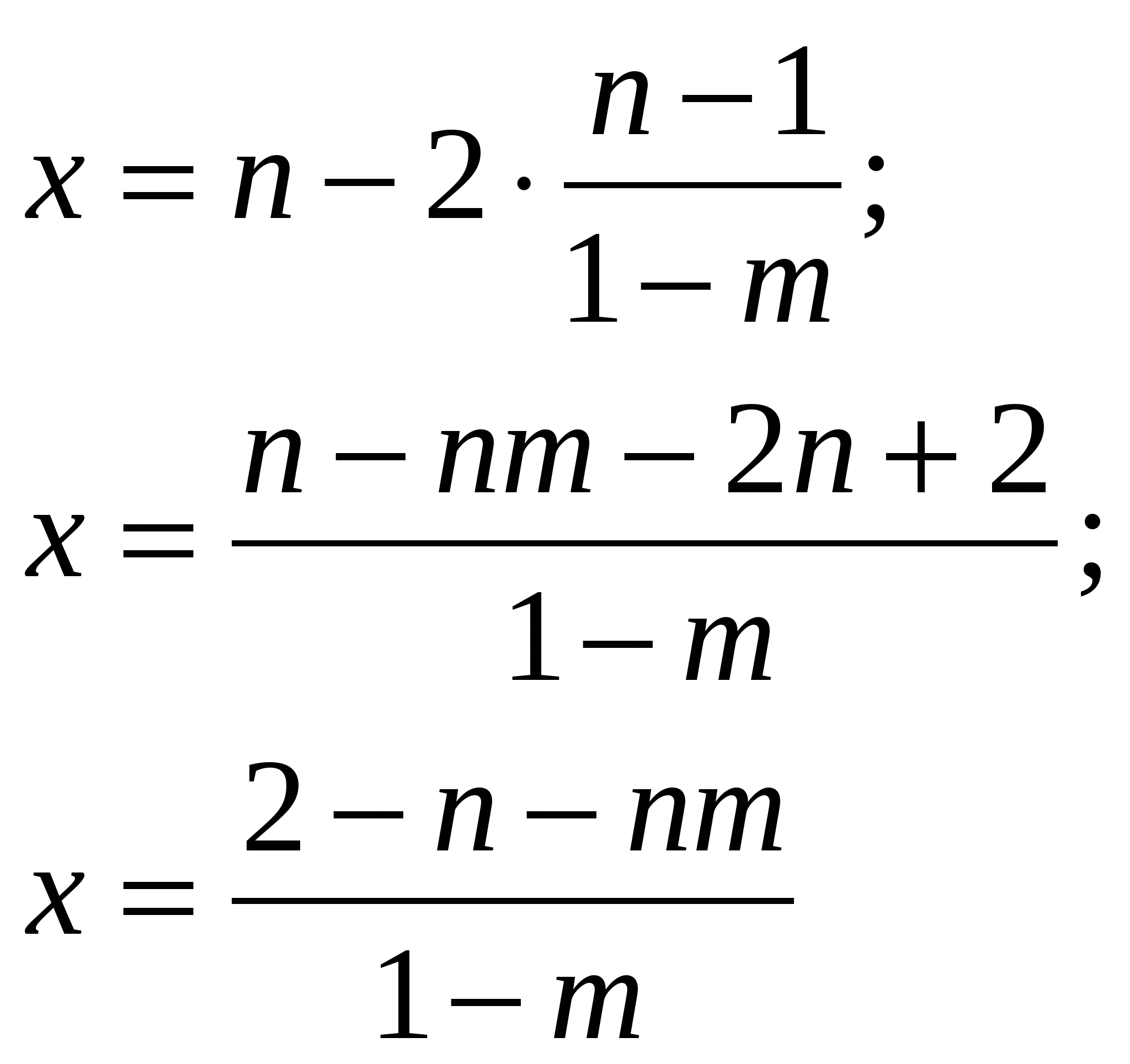
Итак, при m 1 решением системы является пара .



б) Система не имеет решений, если , то есть при m =1, n1.



в) Система имеет бесконечно много решений, если , то есть m =1, n =1.



Пары вида , где x₀ - любое число, являются решением системы в этом случае.



Ответ: если m =1, n1 то решений нет; если m =1, n =1, то решений бесконечное множество ;



если mи n - любое число, то решение единственное: .

Рассмотрим еще примеры решений систем уравнений с параметрами.

Пример 3. Найти все значения параметра b, при каждом из которых система уравнений (1) имеет хотя бы одно решение.

Решение. Из первого уравнения системы следует, что . Подставив это выражение во второе уравнение системы, приходим к равносильной системе:

А) Если b=0 , то система несовместима

Б) Если b=3, то система имеет бесконечно много решений вида

, где а - любое число.

В) Если b ≠ 0, b ≠ 3, то система имеет единственное решение .

Следовательно, данная система имеет хотя бы одно решение при любом b, кроме b = 0.

Ответ: b

Пример. При каких значениях c и d система уравнений

имеет единственное решение х=1, у=1.

Решение. Подставив значения х=1, у=1 в систему , получим

Эта система имеет два решения : а) c = 0, d = 2; б) c = -2, d = 3. Таким образом, только при этих значениях c и d система (1) имеет решения х=1,у=1, но это не означает, что найденные значения параметров c и d обеспечивают единственность решения. Обязательно нужно сделать проверку, чтобы убедиться, действительно ли при этих значениях параметров система имеет единственное решение х=1, у=1.

А) Если с = 0, d = 2, то получим систему, которая имеет единственное решение х = 1, у = 1

Б) Если с = -2, d = 3, то получим систему, которая также имеет единственное решение х=1, у=1

Ответ: с = 0, d = 2 или с = -2, d = 3

Пример 4. При каких значениях а для любого b найдется хотя бы одно с такое, что система (1) имеет по крайней мере одно решение?

Решение.

1. Система (1) при b ≠ ±2 и при любых а и с имеет единственное решение

2. Если b=2, то система (1) приме вид(2)

3. Чтобы система (2) имела решение, должно выполняться условие

, т.е. . Рассматривая последнее соотношение как уравнение относительно с, замечаем, что оно имеет решение при любых а

4. Если b= -2 то система (1) приме вид(3)

5. Чтобы система (3) имела решения, должно выполняться условие

, т.е. . Рассматривая последнее соотношение как квадратное уравнение относительно с, замечаем, что оно имеет решение, если дискриминант Д = 4 + 4а ≥ 0, т.е. 1+а ≥0. Следовательно, а

6. Таким образом, при а всегда найдется такое с , что для любого значения b заданная система имеет по крайней мере одно решение.

Ответ: а

Пример 3. При каких значениях а и b системы уравнений

(1) и (2)

являются равносильными?

Решение. Система (1) имеет единственное решение

при любом значении параметра b.

Поэтому если при некоторых значениях параметров а и b заданные системы равносильны, то система (2) должна иметь то же самое единственное решение. Подставив это решение во второе уравнение системы(2), получим , откуда или b=±1, x0 = 2, y0 = 1 .

Из первого уравнения системы (2) найдем две пары значений а и b:

А) а = 2, b = 1,

Б) а = - 2\3, b = -1,

Проверим, каждая ли из этих пар удовлетворяет условию равносильности систем.

Пусть а = 2, b = 1, тогда система(2) примет вид. Эта система имеет бесконечное множество решений, т.к.. следовательно пара а = 2, b = 1, не обеспечивает равносильность систем (1) и (2).

Пусть а = - 2\3, b = -1, тогда система (2) примет вид иимеет единственное решение x0 = 2, y0 = 1

Ответ: а = - 2\3, b = -1