Тема урока: Окружность, описанная около треугольника

Цель урока: выработать навыки построения описанного около треугольника окружности

Задачи урока: решение задач для закрепления пройденного материала

Ход урока:

1 этап: Орг момент, приветствие, проверка домашнего задания

2 этап: новая тема

Определение.

Окружность называется описанной около треугольника, если все вершины треугольника лежат на окружности.

При этом треугольник называется вписанным в окружность.

OA=OB=OC=R Расстояние от любой вершины треугольника до центра описанной окружности равно радиусу этой окружности.

Окружность </можно описать около любого треугольника.

Центром описанной около треугольника окружности является точка пересечения серединных перпендикуляров к сторонам треугольника (то есть отрезков, перпендикулярных к сторонам треугольника и проходящих через середины этих сторон).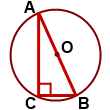

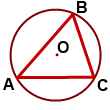
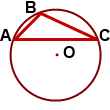
Рис 1 рис 2 рис 3

1. Центр окружности, описанной около остроугольного треугольника, лежит внутри треугольника. Рис 1

2. Центр описанной около прямоугольного треугольника окружности лежит на середине гипотенузы. Рис 2

3. Центр окружности, описанной около тупоугольного треугольника, лежит вне треугольника (напротив тупого угла, за большей стороной). Рис 3

3 этап: решение задач:

№ 220 стр 67 Одна окружность описана около равностороннего треугольника а другая вписана в него докажите что центры этих окружностей совпадают

Решение:

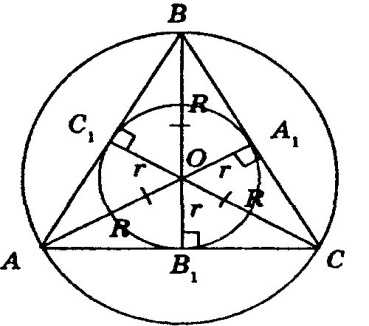
Центр окружности, вписанной в треугольник, является точкой пересечения его биссектрис.

Центр окружности, описанной около треугольника, является точкой пересечения серединных перпендикуляров.

В равностороннем треугольнике биссектрисы являются и медианами и высотами, откуда они являются и серединными перпендикулярами. Значит, центры вписанной и описанной окружности совпадают

№ 221 стр 67 Окружности с радиусами 80 см и 60 см касаются друг друга. Найдите расстояние между центрами окружностей в случаях внешнего и внутреннего касаний.

Решение: внешнее касание - 80+60=140 см внутреннее - 80-60=20 см

№ 222 стр 67 каждая из трёх окружностей проходит через центры двух других. Докажите, что их центры являются вершинами равностороннего треугольника.

Решение

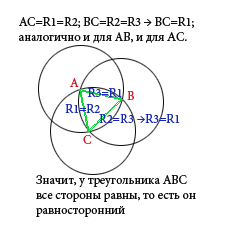
4 этап: подведение итогов

5 этап: домашняя работа № 223 № 224 стр 67