- Учителю
- Построение сечений многогранников на основе аксиоматики (10 класс)
Построение сечений многогранников на основе аксиоматики (10 класс)
Методическая разработка урока по геометрии учителя математики СОШ № 45 с углубленным изучением отдельных предметов Ковалевой Л.Е.
Тема: ''Построение сечений многогранников на основе аксиоматики ''. ( 2 часа )
10 класс
Урок обобщения и систематизации знаний учащихся по геометрии в 1О классе.
Цели урока:
1.Дидактические.
а) перед учащимися ставятся последовательно одна за другой посильные теоретические практические задачи, решение которых дает им новые знания.
в) С помощью задач, последовательно связанных друг с другом, ознакомить учеников даже с довольно сложными математическими теориями.
2. Воспитательные.
Аккуратность, коллективизм, ответственность за себя и товарищей, дружбу, любовь к предмету и др.
3. Прикладные.
Умение анализировать задачу, работать с учебником, применять свои знания в новой ситуации.
ТЕМЫ выступлений для урока
1. Аксиомы стереометрии (таблицы остаются учащимся для работы).
А 1. Через любые две точки пространства проходит единственная прямая.
А 2. Через любые три точки пространства, не лежащие на одной прямой, проходит единственная плоскость.
А 3. Если две плоскости имеют общую точку, то они пересекаются по прямой.
Аксиома
Чертеж
Запись
А1
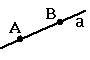
А,В а, а - единственная прямая
А2
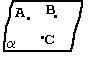
А, В, С ![]() одной прямой. А, В, С
одной прямой. А, В, С![]()
![]() ,
, ![]() - единственная плоскость.
- единственная плоскость.
А3
с![]()
![]() ;
;![]()
![]()
![]()
![]() =с, С
=с, С![]() с.
с.
В ходе беседы выделяются существенные моменты теории:
а) разъяснить содержание аксиом и иллюстрировать на модели;
б) чтение учащимися текста аксиом;
в) выполнение чертежа;
г) запись содержания с помощью символов.
2. Следствия из аксиом стереометрии.
Чертеж.
Формулировка.
Сл.1
Если две точки прямой принадлежат плоскости, то и вся прямая принадлежит этой плоскости.
Сл.2
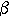
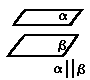
Через прямую и не лежащую на ней точку можно провести плоскость и притом только одну.
Сл.3.
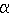
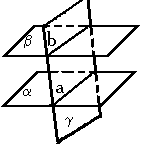
Через две пересекающиеся прямые можно провести плоскость и притом только одну.
В заключение предлагается схема логического строения геометрии (заготовленная заранее):
3. а) Взаимное расположение в пространстве двух прямых.
б) Взаимное расположение в пространстве прямой и плоскости.
в) Взаимное расположение в пространстве двух плоскостей.
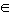
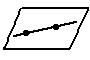
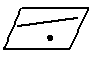
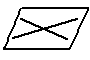
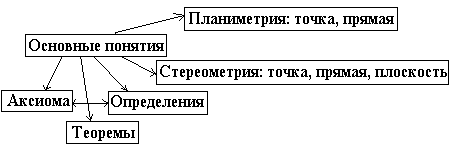
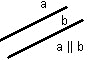
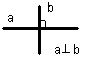
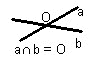

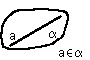
г) Свойства, связывающие понятие параллельности двух плоскостей с понятием параллельности двух прямых.
Теорема. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.
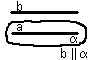
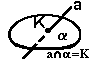
Теорема (признак). Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.
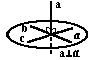
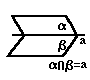
4. Способы задания плоскостей.
Способы задания плоскостей
Рисунок
I. По трем точкам
A2
2. По прямой и не принадлежащей ей точке.
Cл 2
3. По двум пересекающимся прямым.
Cл 3
4. По двум параллельным прямым.
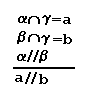
определение параллельных прямых
5. Используя полученные знания, применим их к построению сечений многогранников на основе аксиоматики:
Примеры и их решение приводят учащиеся (под руководством учителя).
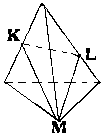
N1. Построить сечение, определенное точками K, L, M.
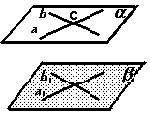
N2. Построить сечение, определяемое параллельными прямыми АА1 и CC1.
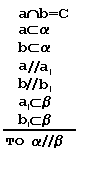 AA1//CC1
AA1//CC1
N3. АС1 и А1С. АС1 ![]() А1С.
А1С.
N4. Построить сечение по прямой и точке: BC и М.
6. Построение сечений с использованием свойств параллельных плоскостей.
N1. Определите вид и найдите периметр сечения куба АВСДА1В1С1Д1 плоскостью, проходящей через ребро А1Д1 и середину ребра ВВ1, если длина ребра куба равна 8 см.
 P=16+8
P=16+8![]() =8(2+
=8(2+![]() )см
)см
N2. Определите вид и найдите периметр сечения куба АВСДА1В1С1Д1 плоскостью, проходящей через точки А, Д и середину ребра СС1, если длина ребра куба равна 4 см.
 P=8+4
P=8+4![]() =4(2+
=4(2+![]() )см
)см
N3. Определите вид сечения (и постройте его) куба АВСДА1В1С1Д1 плоскостью, проходящей через точку М ![]() В1С1 и диагональ нижнего основания.
В1С1 и диагональ нижнего основания.
7.
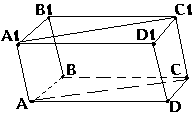
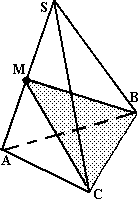
N1. Построить сечение правильной призмы плоскостью, проходящей через ребро АВ и середину ребра В1С1.
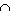
N2. Построить сечение пирамиды плоскостью, проходящей через точку К и параллельно плоскости основания пирамиды.
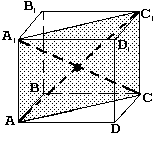
N3. Построить сечение призмы плоскостью, проходящей через точку К и параллельно плоскости грани АВВ1А1.
8. Подведение итогов
9. Домашнее задание:
Составить две задачи на построение сечений многогранников с использованием полученных знаний.
Решение задач должно сопровождаться работой учащихся на моделях, изготовленных из спиц, спичек, пластилина или пенопласта. Учащиеся должны изготовить сечения из картона и использовать его при выполнении чертежа на бумаге. Такой поиск решения (руками) помогает при построении сечения.