Учителю
Рабочая программа по геометрии 8 класс учебник Атанасян

Рабочая программа по геометрии 8 класс учебник Атанасян

Автор публикации: Пермякова С.В.

Дата публикации: 20.06.2016

Краткое описание:

предварительный просмотр материала

Муниципальное бюджетное общеобразовательное учреждение

гимназия № 5

РАССМОТРЕНО

Педагогический совет

Протокол № 1

« » августа 2016 г.

УТВЕРЖДЕНО

Директор МБОУ гимназия № 5

_________ /Перепечай Э.М./

Пр № « » августа 2016г.

Рабочая учебная программа

по геометрии для 8 класса

Составитель:

Учитель математики

МБОУ гимназия № 5

Пермякова С.В.

2016 - 2017 учебный год

г. Хабаровск

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Рабочая программа по геометрии для 8 класса составлена на основе Федерального государственного образовательного стандарта базового уровня общего образования, утвержденного приказом Министерства образования и науки РФ от 05.03.2004г. № 1089 (в ред. Приказов Минобрнауки РФ от 03.06.2008 №164, от 31.08.2009 № 320, от 19.10.2009 № 427); примерной программы основного общего образования по геометрии, с учетом программы общеобразовательных учреждений «Геометрия. 8 класс» / Сост. Т.А. Бурмистрова - 2 издание. Москва. «Просвещение» 2009г.

Рабочая программа конкретизирует содержание предметных тем образовательного стандарта, позволяет распределить учебные часы по разделам курса.

Программа реализуется с помощью УМК Л.С. Атанасяна, включённого в федеральный и региональный перечень учебников.

В рабочей программе представлены содержание математического образования, требования к обязательному и возможному уровню подготовки обучающегося, виды контроля, а также компьютерное обеспечение урока.

Основными (планируемыми) учебными проектами в 8 классе являются:

В мире четырехугольников;
Вычисление площадей в повседневной жизни;
Окружность Эйлера - поиск закономерностей.

УМК по дисциплине:

Геометрия 7-9 класс: Учебник для общеобразовательных учреждений/ А.С. Атанасян, В.Ф. Бутузова/15 -е издание. Москва. «Просвещение» 2013г.

Срок реализации: один учебный год.

Общая характеристика учебного предмета

Математическое образование в основной школе складывается из следующих содержательных компонентов (точные названия блоков): арифметика; алгебра; геометрия; элементы комбинаторики, теории вероятностей, статистики и логики. В своей совокупности они отражают богатый опыт обучения математике в нашей стране, учитывают современные тенденции отечественной и зарубежной школы и позволяют реализовать поставленные перед школьным образованием цели на информационно емком и практически значимом материале. Эти содержательные компоненты, развиваясь на протяжении всех лет обучения, естественным образом переплетаются и взаимодействуют в учебных курсах.

Геометрия - один из важнейших компонентов математического образования, необходимая для приобретения конкретных знаний о пространстве и практически значимых умений, формирования языка описания объектов окружающего мира, для развития пространственного воображения и интуиции, математической культуры, для эстетического воспитания учащихся. Изучение геометрии вносит вклад в развитие логического мышления, в формирование понятия доказательства.

Изучение математики на уровне основного общего образования направлено на достижение следующих целей:

- овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;

- интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе, свойственных математической деятельности: ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;

- формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;

- воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, играющей особую роль в общественном развитии.

Цели изучения курса геометрии в 8 классе:

создание условий для умения логически обосновывать суждения, выдвигать гипотезы и понимать необходимость их проверки;
создание условий для умения ясно, точно и грамотно выражать свои мысли в устной и письменной речи;
формирование умения использовать различные языки математики: словесный, символический, графический;
формирование умения свободно переходить с языка на язык для иллюстрации, интерпретации, аргументации и доказательства;
создание условий для плодотворного участия в работе в группе; умения самостоятельно и мотивированно организовывать свою деятельность;
формирование умения использовать приобретенные знания и умения в практической деятельности и повседневной жизни для исследования (моделирования) несложных практических ситуаций на основе изученных;
сформировать понятие основных плоских геометрических фигур и их свойств.

Задачи изучения курса геометрии в 8 классе:

систематизировать сведения о четырёхугольниках;
сформировать представления о фигурах, симметричных относительно точки и прямой;
сформировать понятие площади многоугольника;
развить умение вычислять площади фигур;
сформировать понятие подобных треугольников;
выработать умение применять признаки подобия в процессе доказательства теорем и решении задач;
сформировать навыки решения прямоугольных треугольников;
расширить сведения об окружности.

В курсе геометрии 8-го класса продолжается решение задач на признаки равенства треугольников, но в совокупности с применением новых теоретических фактов. Теорема о сумме углов выпуклого многоугольника позволяет расширить класс задач. Формируются практические навыки вычисления площадей многоугольников в ходе решения задач. Особое внимание уделяется применению подобия треугольников к доказательствам теорем и решению задач. Вводятся первые знания о синусе, косинусе и тангенсе острого угла прямоугольного треугольника. Систематизируются сведения об окружности и её свойствах, вписанной и описанной окружностях. Серьезное внимание уделяется формированию умений рассуждать, выполнять простые доказательства, давать обоснования выполняемых действий. Параллельно закладываются основы для изучения систематических курсов стереометрии, физики, химии и других смежных предметов.

Место учебного предмета в учебном плане.

Согласно учебному плану на изучение геометрии на уровне основного общего образования в 8 классе отводится 68 ч из расчета 2 ч в неделю.

Количество учебных часов, на которые рассчитана программа:

68 часов (по 2 часов в неделю);

Плановых контрольных работ - шесть (тематических - 5; итоговая - 1).

Формы промежуточной и итоговой аттестации: контрольные работы, самостоятельные работы, тесты.

Уровень обучения - базовый.

Результаты освоения учебного предмета.

Результаты обучения представлены в «Требованиях к уровню подготовки», задающих систему итоговых результатов обучения, которые должны быть достигнуты всеми учащимися, оканчивающими 8 класс, и достижение которых является обязательным условием положительной аттестации ученика за курс 8 класса. Эти требования структурированы по трем компонентам: «знать/понимать», «уметь», «использовать приобретенные знания и умения в практической деятельности и повседневной жизни».

Требования к уровню подготовки учащихся 8 классов

Знать/понимать:

значение математической науки для решения задач, возникающих в теории и практике; широту и в тоже время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
значение практики и вопросов, возникающих в самой математике для формирования и развития математической науки; историю развития понятия числа, возникновения и развития геометрии;
универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности; вероятностный характер всех процессов окружающего мира;

Уметь:

распознавать плоские геометрические фигуры, различать их взаимное расположение, аргументировать суждения, использовать определения, свойства, признаки;
изображать планиметрические фигуры, выполнять чертежи по условию задач, осуществлять преобразование фигур;
вычислять значения геометрических величин (длин, углов, площадей)
решать геометрические задачи, опираясь на изученные свойства фигур отношений между ними, применяя дополнительные построения, алгебраический и простейший тригонометрический аппарат, соображения симметрии;
проводить доказательные рассуждения при решении задач, используя известные теоремы;
решать основные задачи на построение с помощью циркуля и линейки:
решать простейшие планиметрические задачи.

Владеть компетенциями: познавательной, коммуникативной, информационной и рефлексивной.

Решать следующие жизненно практические задачи:

самостоятельно приобретать и применять знания в различных ситуациях, работать в группах;
аргументировать и отстаивать свою точку зрения;
уметь слушать других, извлекать учебную информацию на основе сопоставительного анализа объектов;
пользоваться предметным указателем энциклопедий и справочников для нахождения информации, самостоятельно действовать в ситуации неопределённости при решении актуальных проблем.

Использовать приобретённые знания и умения в практической деятельности и в

повседневной жизни для:

вычисления длин, площадей основных геометрических фигур с помощью формул, используя при необходимости справочники и технические средства;
описания реальных ситуаций на языке геометрии;
расчетов, включающих простейшие формулы;
решения геометрических задач с использованием тригонометрии;
построений геометрическими инструментами (линейка, угольник, циркуль, транспортир).

Общеучебные умения, навыки и способы деятельности

В ходе преподавания геометрии в 8 классе, работы над формированием у обучающихся перечисленных в программе знаний и умений следует обращать внимание на то, чтобы они овладевали умениями общеучебного характера, разнообразными способами деятельности, приобретали опыт:

планирования и осуществления алгоритмической деятельности, выполнения заданных и конструирования новых алгоритмов;
решения разнообразных классов задач из различных разделов курса, в том числе задач, требующих поиска пути и способов решения;
исследовательской деятельности, развития идей, проведения экспериментов, обобщения, постановки и формулирования новых задач;
ясного, точного, грамотного изложения своих мыслей в устной и письменной речи, использования различных языков математики (словесного, символического, графического), свободного перехода с одного языка на другой для иллюстрации, интерпретации, аргументации и доказательства;
проведения доказательных рассуждений, аргументации, выдвижения гипотез и их обоснования;
поиска, систематизации, анализа и классификации информации, использования разнообразных информационных источников, включая учебную и справочную литературу, современные информационные технологии.

Для оптимизации образовательного процесса предполагается использование возможностей различных типов уроков:

Урок-лекция. Предполагаются совместные усилия учителя и учеников для решения общей проблемной познавательной задачи. На таком уроке используется демонстрационный материал на компьютере, разработанный учителем или учениками, мультимедийные продукты.
Урок-практикум. На уроке учащиеся работают над различными заданиями в зависимости от своей подготовленности. Виды работ могут быть самыми разными: письменные исследования, решение различных задач, изучение свойств различных функций, практическое применение различных методов решения задач. Компьютер на таких уроках используется как электронный калькулятор, тренажер устного счета, виртуальная лаборатория, источник справочной информации.
Урок-исследование. На уроке учащиеся решают проблемную задачу исследовательского характера аналитическим методом и с помощью компьютера с использованием различных лабораторий.
Комбинированный урок предполагает выполнение работ и заданий разного вида.
Урок-игра. На основе игровой деятельности учащиеся познают новое, закрепляют изученное, отрабатывают различные учебные навыки.
Урок решения задач. Вырабатываются у учащихся умения и навыки решения задач на уровне обязательной и возможной подготовке. Любой учащийся может использовать компьютерную информационную базу по методам решения различных задач, по свойствам элементарных функций и т.д.
Урок-тест. Тестирование проводится с целью диагностики пробелов знаний, контроля уровня обученности учащихся, тренировки технике тестирования. Тесты предлагаются как в печатном так и в компьютерном варианте. Причем в компьютерном варианте всегда с ограничением времени, используя электронную систему контроля знаний.
Урок-самостоятельная работа. Предлагаются разные виды самостоятельных работ.
Урок-контрольная работа. Проводится с целью контроля знаний учащихся по пройденной теме.

Критерии и нормы оценки знаний и умений учащихся

Оценка «5» ставится в случае:

1. Знания, понимания, глубины усвоения обучающимися всего объёма программного материала.

2. Умения выделять главные положения в изученном материале, на основании фактов и примеров обобщать, делать выводы, устанавливать межпредметные и внутрипредметные связи, творчески применять полученные знания в незнакомой ситуации.

3. Отсутствия ошибок и недочётов при воспроизведении изученного материала, при устных ответах устранения отдельных неточностей с помощью дополнительных вопросов учителя, соблюдения культуры письменной и устной речи, правил оформления письменных работ.

Оценка «4» ставится в случае:

1. Знания всего изученного программного материала.

2. Умения выделять главные положения в изученном материале, на основании фактов и примеров обобщать, делать выводы, устанавливать внутрипредметные связи, применять полученные знания на практике.

3. Допущения незначительных (негрубых) ошибок, недочётов при воспроизведении изученного материала; соблюдения основных правил культуры письменной и устной речи, правил оформления письменных работ.

Оценка «3» ставится в случае:

1. Знания и усвоения материала на уровне минимальных требований программы, затруднения при самостоятельном воспроизведении, возникновения необходимости незначительной помощи преподавателя.

2. Умения работать на уровне воспроизведения, затруднения при ответах на видоизменённые вопросы.

3. Наличия грубой ошибки, нескольких грубых ошибок при воспроизведении изученного материала; незначительного несоблюдения основных правил культуры письменной и устной речи, правил оформления письменных работ.

Оценка «2» ставится в случае:

1. Знания и усвоения материала на уровне ниже минимальных требований программы; наличия отдельных представлений об изученном материале.

2. Отсутствия умения работать на уровне воспроизведения, затруднения при ответах на стандартные вопросы.

3. Наличия нескольких грубых ошибок, большого числа негрубых при воспроизведении изученного материала, значительного несоблюдения основных правил культуры письменной и устной речи, правил оформления письменных работ.

Оценка «1» ставится в случае:

1. Нет ответа.

Критерии и нормы оценки знаний и умений учащихся за устный ответ.

Оценка "5" ставится, если ученик:

1.Показывает глубокое и полное знание и понимание всего программного материала; полное понимание сущности рассматриваемых понятий, явлений и закономерностей, теорий, взаимосвязей.

2.Умеет составить полный и правильный ответ на основе изученного материала; выделять главные положения, самостоятельно подтверждать ответ конкретными примерами, фактами; самостоятельно и аргументировано делать анализ, обобщения, выводы; устанавливать межпредметные связи (на основе ранее приобретённых знаний) и внутрипредметные связи, творчески применять полученные знания в незнакомой ситуации; последовательно, чётко, связно, обоснованно и безошибочно излагать учебный материал.

Умеет составлять ответ в логической последовательности с использованием принятой терминологии; делать собственные выводы; формулировать точное определение и истолкование основных понятий, законов, теорий.

Может при ответе не повторять дословно текст учебника; излагать, материал литературным языком; правильно и обстоятельно отвечать на дополнительные вопросы учителя; самостоятельно и рационально использовать наглядные пособия, справочные материалы, учебник, дополнительную литературу, первоисточники; применять систему условных обозначений при ведении записей, сопровождающих ответ; использовать для доказательства выводов из наблюдений и опытов.

3. Самостоятельно, уверенно и безошибочно применяет полученные знания в решении проблем на творческом уровне; допускает не более одного недочёта, который легко исправляет по требованию учителя; имеет необходимые навыки работы с приборами, чертежами, схемами, графиками, картами, сопутствующими ответу; записи, сопровождающие ответ, соответствуют требованиям.

Оценка "4" ставится, если ученик:

1. Показывает знания всего изученного программного материала. Даёт полный и правильный ответ на основе изученных теорий; допускает незначительные ошибки и недочёты при воспроизведении изученного материала, небольшие неточности при использовании научных терминов или в выводах, обобщениях из наблюдений. Материал излагает в определённой логической последовательности, при этом допускает одну негрубую ошибку или не более двух недочётов, которые может исправить самостоятельно при требовании или небольшой помощи преподавателя; подтверждает ответ конкретными примерами; правильно отвечает на дополнительные вопросы учителя.

2.Умеет самостоятельно выделять главные положения в изученном материале; на основании фактов и примеров обобщать, делать выводы. Устанавливать внутрипредметные связи. Может применять полученные знания на практике в видоизменённой ситуации, соблюдать основные правила культуры устной речи; использовать при ответе научные термины.

3. Не обладает достаточным навыком работы со справочной литературой, учебником, первоисточником (правильно ориентируется, но работает медленно).

Оценка "3" ставится, если ученик:

1. Усваивает основное содержание учебного материала, но имеет пробелы, не препятствующие дальнейшему усвоению программного материала.

2. Излагает материал несистематизированно, фрагментарно, не всегда последовательно; показывает недостаточно сформированности отдельных знаний и умений; слабо аргументирует выводы и обобщения, допускает ошибки при их формулировке; не использует в качестве доказательства выводы и обобщения из наблюдений, опытов или допускает ошибки при их изложении; даёт нечёткие определения понятий.

3. Испытывает затруднения в применении знаний, необходимых для решения задач различных типов, практических заданий; при объяснении конкретных явлений на основе теорий и законов; отвечает неполно на вопросы учителя или воспроизводит содержание текста учебника, но недостаточно понимает отдельные положения, имеющие важное значение в этом тексте, допуская одну-две грубые ошибки.

Оценка "2" ставится, если ученик:

1. Не усваивает и не раскрывает основное содержание материала; не знает или не понимает значительную часть программного материала в пределах поставленных вопросов; не делает выводов и обобщений.

2. Имеет слабо сформированные и неполные знания, не умеет применять их при решении конкретных вопросов, задач, заданий по образцу.

3. При ответе на один вопрос допускает более двух грубых ошибок, которые не может исправить даже при помощи учителя.

Оценка «1» ставится в случае: 1. Нет ответа.

Критерии и нормы оценки знаний и умений учащихся за самостоятельные письменные и контрольные работы.

Оценка «5» ставится, если ученик:

1. Выполняет работу без ошибок и /или/ допускает не более одного недочёта.

2. Соблюдает культуру письменной речи; правила оформления письменных работ.

Оценка «4» ставится, если ученик:

1. Выполняет письменную работу полностью, но допускает в ней не более одной негрубой ошибки и одного недочёта и /или/ не более двух недочётов.

2. Соблюдает культуру письменной речи, правила оформления письменных работ, но -допускает небольшие помарки при ведении записей.

Оценка «3» ставится, если ученик:

1. Правильно выполняет не менее половины работы.

2. Допускает не более двух грубых ошибок, или не более одной грубой, одной негрубой ошибки и одного недочёта, или не более трёх негрубых ошибок, или одной негрубой ошибки и трёх недочётов, или при отсутствии ошибок, но при наличии пяти недочётов.

3. Допускает незначительное несоблюдение основных норм культуры письменной речи, правил оформления письменных работ.

Оценка «2» ставится, если ученик:

1. Правильно выполняет менее половины письменной работы.

2. Допускает число ошибок и недочётов, превосходящее норму, при которой может быть выставлена оценка "3".

3. Допускает значительное несоблюдение основных норм культуры письменной речи, правил оформления письменных работ.

Оценка «1» ставится в случае:

1. Нет ответа.

Примечание. Учитель имеет право поставить ученику оценку выше той, которая предусмотрена нормами, если им работа выполнена в оригинальном варианте.

Содержание учебного предмета.

Тема 1. «Четырехугольники» (Глава 5).

Многоугольник, выпуклый многоугольник, четырехугольник. Параллелограмм, его свойства и признаки. Трапеция. Прямоугольник, ромб, квадрат, их свойства. Осевая и центральная симметрии.

Цель: изучить наиболее важные виды четырехугольников - параллелограмм, прямоугольник, ромб, квадрат, трапецию; дать представление о фигурах, обладающих осевой или центральной симметрией.

Доказательства большинства теорем данной темы и решения многих задач проводятся с помощью признаков равенства треугольников, поэтому полезно их повторить, в начале изучения темы.

Осевая и центральная симметрии вводятся не как преобразование плоскости, а как свойства геометрических фигур, в частности четырехугольников. Рассмотрение этих понятий как движений плоскости состоится в 9 классе.

Раздел математики. Сквозная линия.

Геометрические фигуры и их свойства.
Измерение геометрических величин.

Обязательный минимум содержания образовательной области математика

Выпуклые многоугольники.
Сумма углов выпуклого многоугольника.
Параллелограмм, его свойства и признаки.
Прямоугольник, квадрат, ромб, их свойства и признаки.
Трапеция, средняя линия трапеции; равнобедренная трапеция.
Теорема Фалеса.

Уровень обязательной подготовки обучающегося

Знать различные виды четырехугольников, их признаки и свойства.
Уметь применять свойства четырехугольников при решении простых задач.

Уровень возможной подготовки обучающегося

Уметь решать геометрические задачи, опираясь на изученные свойства фигур и отношений между ними.
Уметь решать задачи на построение.

Уровень обязательной подготовки выпускника

Меньшая сторона прямоугольника равна 6 см. Найдите длины диагоналей, если они пересекаются под углом 60⁰.

Уровень возможной подготовки выпускника

В параллелограмме ABCD проведена биссектриса угла А, которая пересекает сторону ВС в точке F. Докажите, что треугольник АВF равнобедренный
Постройте прямоугольник по стороне и диагонали.

Тема 2. «Площади фигур» (Глава 6).

Понятие площади многоугольника. Площади прямоугольника, параллелограмма, треугольника, трапеции. Теорема Пифагора.

Цель: расширить и углубить полученные в 5-6 классах представления обучающихся об измерении и вычислении площадей; вывести формулы площадей прямоугольника, параллелограмма, треугольника, трапеции; доказать одну из главных теорем геометрии - теорему Пифагора.

Вывод формул для вычисления площадей прямоугольника, параллелограмма, треугольника, трапеции основывается на двух основных свойствах площадей, которые принимаются исходя из наглядных представлений, а также на формуле площади квадрата, обоснование которой не является обязательным для обучающихся.

Нетрадиционной для школьного курса является теорема об отношении площадей треугольников, имеющих по равному углу. Она позволяет в дальнейшем дать простое доказательство признаков подобия треугольников. В этом состоит одно из преимуществ, обусловленных ранним введением понятия площади. Доказательство теоремы Пифагора основывается на свойствах площадей и формулах для площадей квадрата и прямоугольника. Доказывается также теорема, обратная теореме Пифагора.

Раздел математики. Сквозная линия.

Геометрические фигуры и их свойства.
Измерение геометрических величин.

Обязательный минимум содержания образовательной области математика

Понятие о площади плоских фигур.
Равносоставленные и равновеликие фигуры.
Площадь прямоугольника.
Площадь параллелограмма.
Площадь треугольника.
Площадь трапеции.
Теорема Пифагора

Дополнительные вопросы:

Формула Герона

Уровень обязательной подготовки обучающегося

Уметь пользоваться языком геометрии для описания предметов окружающего мира.
Уметь вычислять значения площадей основных геометрических фигур и фигур, составленных из них;
Знать формулы вычисления площадей геометрических фигур, теорему Пифагора и уметь применять их при решении задач.
Уметь выполнять чертежи по условию задач

Уровень возможной подготовки обучающегося

Знать формулы вычисления площадей геометрических фигур, теорему Пифагора, формулу Герона и уметь применять их при решении задач.
Уметь решать геометрические задачи, опираясь на изученные свойства фигур и отношений между ними, применяя дополнительные построения, алгебраический аппарат, идеи симметрии.
Уметь решать задачи на доказательство и использовать дополнительные формулы для нахождения площадей геометрических фигур.

Уровень обязательной подготовки выпускника

Найдите площадь равнобокой трапеции, если ее основания равны 12 см и 6 см, а боковая сторона образует с одним из оснований угол, равный 45⁰.
В прямоугольнике ABCD найдите AD, если АВ = 5, АС = 13.

Уровень возможной подготовки выпускника

В ромбе высота, равная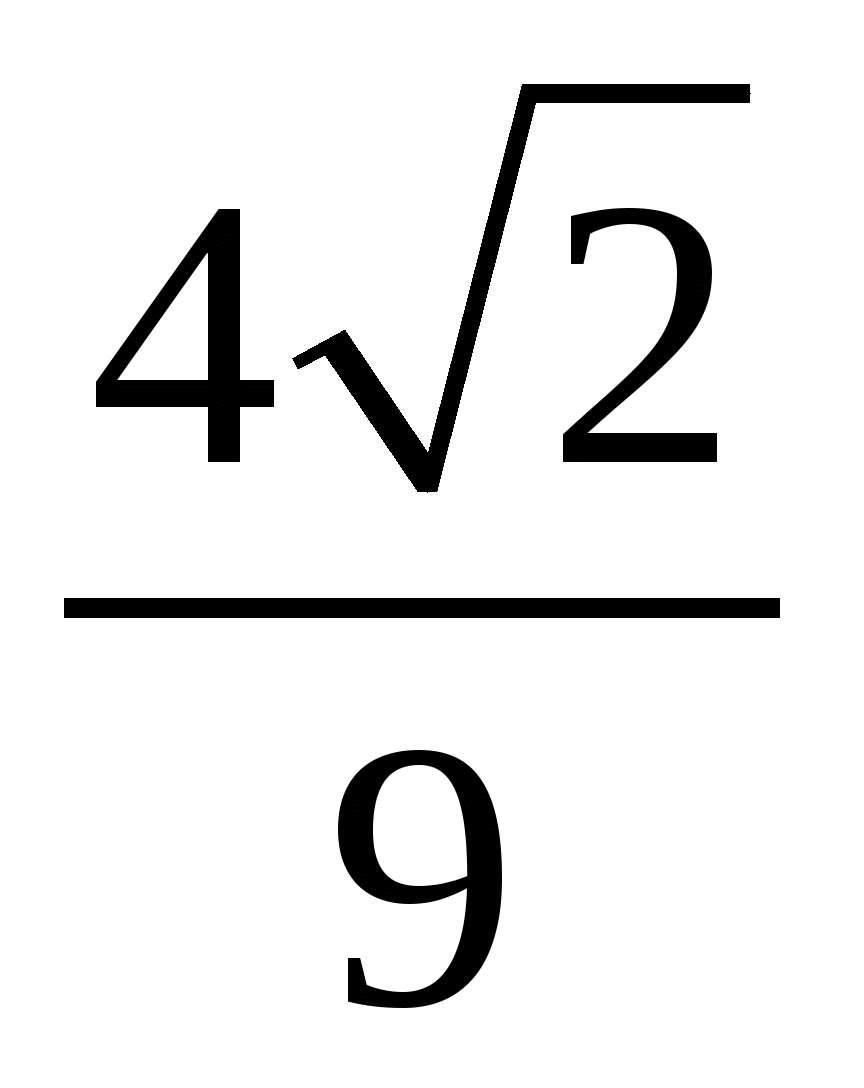см, составляет 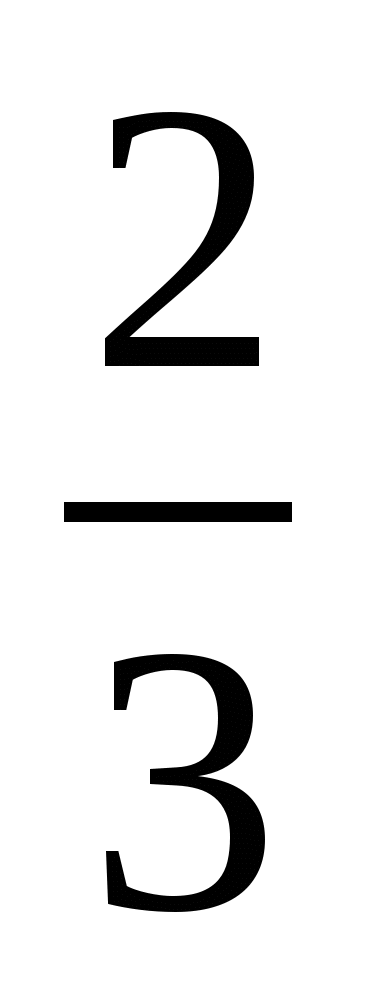большей диагонали. Найдите площадь ромба.
В равнобедренном треугольнике АВС с основанием ВС высота АD равна 8 см. Найдите площадь треугольника АВС, если медиана DM треугольника АDС равна 8 см.

Тема 3. «Подобные треугольники» (Глава 7).

Подобные треугольники. Признаки подобия треугольников. Применение подобия к доказательству теорем и решению задач. Синус, косинус и тангенс острого угла прямоугольного треугольника.

Цель: ввести понятие подобных треугольников; рассмотреть признаки подобия треугольников и их применения; сделать первый шаг в освоении учащимися тригонометрического аппарата геометрии.

Определение подобных треугольников дается не на основе преобразования подобия, а через равенство углов и пропорциональность сходственных сторон.

Признаки подобия треугольников доказываются с помощью теоремы об отношении площадей треугольников, имеющих по равному углу.

На основе признаков подобия доказывается теорема о средней линии треугольника, утверждение о точке пересечения медиан треугольника, а также два утверждения о пропорциональных отрезках в прямоугольном треугольнике. Дается представление о методе подобия в задачах на построение.

В заключение темы вводятся элементы тригонометрии - синус, косинус и тангенс острого угла прямоугольного треугольника.

Раздел математики. Сквозная линия.

Геометрические фигуры и их свойства.
Измерение геометрических величин.

Обязательный минимум содержания образовательной области математика

Подобие треугольников; коэффициент подобия.
Признаки подобия треугольников.
Связь между площадями подобных фигур.
Синус, косинус, тангенс, котангенс острого угла прямоугольного треугольника.
Решение прямоугольных треугольников.
Основное тригонометрическое тождество.

Уровень обязательной подготовки обучающегося

Знать определение подобных треугольников.
Уметь применять подобие треугольников при решении несложных задач.
Уметь пользоваться языком геометрии для описания предметов окружающего мира.
Уметь распознавать геометрические фигуры, различать их взаимное расположение.
Уметь изображать геометрические фигуры.
Уметь выполнять чертежи по условию задач.
Знать признаки подобия треугольников, уметь применять их для решения практических задач.
Уметь находить синус, косинус, тангенс и котангенс острого угла прямоугольного треугольника.

Уровень возможной подготовки обучающегося

Уметь решать геометрические задачи, опираясь на изученные свойства фигур и отношений между ними.
Уметь применять признаки подобия треугольников для решения практических задач.
Уметь проводить доказательные рассуждения при решении задач, используя известные теоремы.
Уметь решать геометрические задачи на соотношения между сторонами и углами прямоугольного треугольника.

Уровень обязательной подготовки выпускника

В трапеции ABCD проведены диагонали АС и ВD, которые пересекаются в точке О. Докажите, что треугольник СОВ подобен треугольнику AOD.

Уровень возможной подготовки выпускника

Докажите, что середины сторон ромба являются вершинами прямоугольника.
Постройте треугольник, если даны середины его сторон.
Биссектрисы MD и NK треугольника MNP пересекаются в точке О. Найдите отношение ОК:ON, если MN = 5 см, NP = 3 см, MP = 7 см.

Тема 4. «Окружность» (Глава 8).

Взаимное расположение прямой и окружности. Касательная к окружности, ее свойство и признак. Центральные и вписанные углы. Четыре замечательные точки треугольника. Вписанная и описанная окружности.

Цель: расширить сведения об окружности, полученные учащимися в 7 классе; изучить новые факты, связанные с окружностью; познакомить обучающихся с четырьмя замечательными точками треугольника.

В данной теме вводится много новых понятий и рассматривается много утверждений, связанных с окружностью. Для их усвоения следует уделить большое внимание решению задач.

Утверждения о точке пересечения биссектрис треугольника и точке пересечения серединных перпендикуляров к сторонам треугольника выводятся как следствия из теорем о свойствах биссектрисы угла и серединного перпендикуляра к отрезку. Теорема о точке пересечения высот треугольника (или их продолжений) доказывается с помощью утверждения о точке пересечения серединных перпендикуляров.

Наряду с теоремами об окружностях, вписанной в треугольник и описанной около него, рассматриваются свойство сторон описанного четырехугольника и свойство углов вписанного четырехугольника.

Раздел математики. Сквозная линия

Геометрические фигуры и их свойства.
Измерение геометрических величин.

Обязательный минимум содержания образовательной области математика

Центральный, вписанный угол; величина вписанного угла.
Взаимное расположение прямой и окружности.
Касательная и секущая к окружности.
Равенство касательных, проведенных из одной точки.
Замечательные точки треугольника: точки пересечения серединных перпендикуляров, биссектрис, медиан.
Окружность, вписанная в треугольник.
Окружность, описанная около треугольника.

Уровень обязательной подготовки обучающегося

Уметь вычислять значения геометрических величин.
Знать свойства биссектрисы угла и серединного перпендикуляра к отрезку.
Уметь распознавать геометрические фигуры, различать их взаимное расположение.
Уметь решать задачи на построение.

Уровень возможной подготовки обучающегося

Уметь решать геометрические задачи, опираясь на изученные свойства фигур и отношений между ними.
Уметь проводить доказательные рассуждения при решении задач, используя известные теоремы.
Знать метрические соотношения в окружности: свойства секущих, касательных, хорд и уметь применять их в решении задач.
Иметь понятие о вписанных и описанных четырехугольниках.

Уровень обязательной подготовки выпускника

Окружность разделена на две дуги, причем градусная мера одной из них в три раза больше градусной меры другой. Чему равны центральные углы, соответствующие этим дугам?
Через точку А окружности проведены диаметр АС и две хорды АВ и AD, равные радиусу этой окружности. Найдите углы четырехугольника АВСD и градусные меры дуг АВ, ВС, CD, AD.

Уровень возможной подготовки выпускника

К данной окружности постройте касательную, проходящую через данную точку вне окружности.
Биссектрисы углов при основании АВ равнобедренного треугольника АВС пересекаются в точке М. Докажите, что прямая СМ перпендикулярна к прямой АВ.
В окружность вписан равнобедренный треугольник АВС с основанием ВС. Найдите углы треугольника, если ВС =102⁰ .

Тема 5. «Повторение. Решение задач»

Раздел математики. Сквозная линия.

Геометрические фигуры и их свойства.
Измерение геометрических величин.

Обязательный минимум содержания образовательной области математика

Выпуклые многоугольники.

Площадь треугольника, четырехугольников.
Теорема Пифагора

Подобие треугольников; коэффициент подобия.
Признаки подобия треугольников.
Решение прямоугольных треугольников.

Окружность.
Построения с помощью циркуля и линейки. Основные задачи на построение.

Уровень обязательной подготовки обучающегося

Уметь пользоваться языком геометрии для описания предметов окружающего мира.
Уметь распознавать геометрические фигуры, различать их взаимное расположение.
Уметь изображать геометрические фигуры.
Уметь выполнять чертежи по условию задач.
Уметь доказывать теоремы о параллельности прямых с использованием соответствующих признаков.
Уметь вычислять значения геометрических величин (длин, углов, площадей).
Уметь решать задачи на построение.

Уровень возможной подготовки обучающегося

Уметь решать геометрические задачи, опираясь на изученные свойства фигур и отношений между ними.
Уметь проводить доказательные рассуждения при решении задач, используя известные теоремы.

Уровень обязательной подготовки выпускника

В равнобедренной трапеции диагональ равна 10 см, а высота равна 6 см. Найдите площадь трапеции.
Два угла треугольника равны 45⁰ и 30⁰. Найдите отношения противолежащих им сторон.
Две окружности с центрами в точках О и О₁ и равными радиусами пересекаются в точках А и В. Докажите, что четырехугольник АО₁ВО - параллелограмм.

Уровень возможной подготовки выпускника

В треугольнике АВС преведена высота ВН. Докажите, что если:

а) угол А острый, то ;

б) угол А тупой, то .

Найдите радиус вписанной в равносторонний треугольник окружности, если радиус описанной окружности равен 10 см.

Тематическое планирование

Отличительные особенности рабочей программы по сравнению с примерной:

В программу внесены изменения: уменьшено или увеличено количество часов на изучение некоторых тем. Сравнительная таблица приведена ниже.

Название темы

Кол-во часов по авторской программе

Кол-во часов по рабочей программе

Кол-во контрольных работ

Вводное повторение

Четырехугольники

Площади фигур

Подобные треугольники

Окружность

Повторение. Решение задач

ИТОГО

Внесение данных изменений позволит охватить весь изучаемый материал по программе, повысить уровень обученности учащихся по предмету, а также более эффективно осуществить индивидуальный подход к обучающимся.

п/п

Тема урока

Кол-во

часов

Характеристика основных видов учебной деятельности учащихся

Повторение

Цель: подготовить учащихся к изучению темы «Четырехугольники».

Вводное повторение. Параллельные прямые (признаки и свойства)

Уметь выполнять задачи из разделов курса VII класса: признаки равенства треугольников; соотношения между сторонами и углами треугольника; признаки и свойства параллельных прямых. Знать понятия: теорема, свойство, признак.

Вводное повторение. Равенство треугольников.

Четырехугольники

Цель: дать учащимся систематические сведения о четырехугольниках и их свойствах; сформировать представления о фигурах, симметричных относительно точки или прямой.

Многоугольники. Сумма углов n-угольника. Основные понятия

Уметь объяснить, какая фигура называется многоугольником, назвать его элементы; знать, что такое периметр многоугольника, какой многоугольник называется выпуклым; уметь вывести формулу суммы углов выпуклого многоугольника и решать задачи типа 364 - 370. Уметь находить углы многоугольников, их периметры.

Четырехугольники. Решение задач

Параллелограмм и его свойства

Знать определения параллелограмма и трапеции, виды трапеций, формулировки свойств и признаков параллелограмма и равнобедренной трапеции, уметь их

доказывать и применять при решении

задач типа 372 - 377, 379 - 383, 39О.

Признаки параллелограмма

Решение задач по теме: «параллелограмм»

Трапеция, ее свойства и признаки

Уметь выполнять деление отрезка на n равных частей с помощью циркуля и линейки; используя свойства параллелограмма и равнобедренной трапеции уметь доказывать некоторые утверждения. Уметь выполнять задачи на построение четырехугольников.

Теорема Фалеса. Задачи на построение

10.

Прямоугольник и его свойства

Знать определения частных видов параллелограмма: прямоугольника, ромба и квадрата, формулировки их свойств и признаков.

Уметь доказывать изученные теоремы и применять их при решении задач типа 401 - 415.

11.

Ромб, квадрат и их свойства

12.

Решение задач по теме: «прямоугольник, ромб, квадрат»

13.

Осевая и центральная симметрия, решение задач.

Знать определения симметричных точек и фигур относительно прямой и точки.

Уметь строить симметричные точки и распознавать фигуры, обладающие осевой симметрией и центральной симметрией.

14.

Решение задач по теме: «четырехугольники»

Уметь применять все изученные формулы при решении задач, в устной форме доказывать теоремы и излагать необходимый теоретический материал

15.

Повторительно-обобщающий урок, подготовка к контрольной работе

16.

Контрольная работа № 1 по теме «Четырехугольники»

Уметь применять все изученные формулы и теоремы при решении задач

Площади фигур

Цель: сформировать понятие площади многоугольника, выработать у учащихся умение находить площадь треугольника, параллелограмма, трапеции, применять теорему Пифагора.

17.

Площадь многоугольника

Знать основные свойства площадей и формулу для вычисления площади прямоугольника. Уметь вывести формулу для вычисления площади прямоугольника и использовать ее при решении задач типа 447 - 454, 457.

18.

Площадь прямоугольника. Решение задач

19.

Площадь параллелограмма

Знать формулы для вычисления площадей параллелограмма, треугольника и трапеции; уметь их доказывать, а также знать теорему об отношении площадей треугольников, имеющих по равному углу, и уметь применять все изученные формулы при решении задач типа 459 - 464, 468 - 472, 474.

20.

Площадь треугольника

21.

Решение задач на нахождение площади треугольника и параллелограмма

22.

Площадь трапеции

23.

Решение задач на вычисление площадей фигур

24.

Теорема Пифагора

Знать теорему Пифагора и обратную ей теорему, область применения, пифагоровы тройки. Уметь доказывать теоремы и применять их при решении задач типа 483 - 499 (находить неизвестную величину в прямоугольном треугольнике).

Теорема, обратная теореме Пифагора. Практическое использование теоремы Пифагора

Решение задач по теме «Теорема Пифагора»

Уметь применять теоремы при решении задач типа 483 - 499 (находить неизвестную величину в прямоугольном треугольнике).

Решение задача по теме: «Площади»

Уметь применять все изученные формулы и теоремы при решении задач; в устной форме доказывать теоремы и излагать необходимый теоретический материал.

Решение задач по теме: «Площади фигур»

Контрольная работа № 2 по теме «Площади фигур»

Уметь применять все изученные формулы и теоремы при решении задач

Подобные треугольники

Цель: сформировать понятие подобных треугольников, выработать умение применять признаки подобия треугольников при решении простейших задач, использовать понятия синуса, косинуса, тангенса острого угла для решения прямоугольных треугольников.

Определение подобных треугольников

Знать определения пропорциональных отрезков и подобных треугольников, теорему об отношении подобных треугольников и свойство биссектрисы треугольника (задача 535).

Уметь определять подобные треугольники, находить неизвестные величины из пропорциональных отношений, применять теорию при решении задач типа 535 - 538, 541.

Отношение площадей подобных треугольников

Первый признак подобия треугольников

Знать признаки подобия треугольников, определение пропорциональных отрезков. Уметь доказывать признаки подобия и применять их при решении задач типа 550 - 555, 559 - 562.

Решение задач на применение первого признака подобия треугольников

Второй и третий признак подобия треугольников

Решение задач на применение II и IIIпризнаков подобия треугольников

Решение задач на применение признаков подобия треугольников

Контрольная работа № 3 по теме «Признаки подобия треугольников»

Уметь применять все изученные теоремы при решении задач, знать отношения периметров и площадей.

Средняя линия треугольника, свойства медиан треугольника

Знать теоремы о средней линии треугольника, точке пересечения медиан треугольника и пропорциональных отрезках в прямоугольном треугольнике. Уметь доказывать эти теоремы и применять при решении задач типа 567, 568, 570, 572 - 577, а также уметь с помощью циркуля и линейки делить отрезок в данном отношении и решать задачи на построение типа 586 - 590.

Пропорциональные отрезки

Пропорциональные отрезки в прямоугольном треугольнике

Измерительные работы на местности

Задачи на построение методом подобия

Решение задач на построение методом подобных треугольников

Синус, косинус и тангенс острого угла прямоугольного треугольника

Знать определения синуса, косинуса и тангенса острого угла прямоугольного треугольника, значения синуса, косинуса и тангенса для углов 30⁰, 45⁰ и 60⁰, метрические соотношения. Уметь доказывать основное тригонометрическое тождество, решать задачи типа 591 - 602.

Значение синуса, косинуса и тангенса для углов 30⁰, 45⁰, 60⁰

Соотношения между сторонами и углами прямоугольного треугольника. Решение задач

Контрольная работа № 4 по теме «Подобные треугольники»

Уметь применять все изученные формулы, значения синуса, косинуса, тангенса, метрические отношения при решении задач

Окружность

Цель: дать учащимся систематические сведения об окружности и ее свойствах, касательной к окружности, вписанных и описанных окружностях.

Взаимное расположение прямой и окружности

Знать возможные случаи взаимного расположения прямой и окружности, определение касательной, свойство и признак касательной. Уметь их доказывать и применять при решении задач типа 631, 633 - 636, 638 - 643, 648, выполнять задачи на построение

окружностей и касательных, определять отрезки хорд окружностей.

Касательная к окружности.

Решение задач по теме «Касательная к окружности».

Градусная мера дуги и окружности

Знать, какой угол называется центральным и какой вписанным, как определяется градусная мера дуги окружности, теорему о вписанном угле, следствия из нее и теорему о произведении отрезков пересекающихся хорд. Уметь доказывать эти теоремы и применять при решении задач типа 651 - 657, 659, 666 - 669.

Теорема о вписанном угле

Теорема об отрезках пересекающихся хорд

Решение задач по теме «Центральные и вписанные углы»

Свойство биссектрисы треугольника

Знать теоремы о биссектрисе угла и о серединном перпендикуляре к отрезку, их следствия, а также теорему о пересечении высот треугольника. Уметь доказывать эти теоремы и применять их при решении задач типа 674 - 679, 682 - 686. Уметь выполнять построение замечательных точек треугольника.

Серединный перпендикуляр

Теорема о точке пересечения высот треугольника

Вписанная и описанная окружность

Знать, какая окружность называется вписанной в многоугольник и какая описанной около многоугольника, теоремы об окружности, вписанной в треугольник, и об окружности, описанной около треугольника, свойства вписанного и описанного четырехугольников. Уметь доказывать эти теоремы и применять при решении задач типа 689 - 696, 701 - 711.

Свойство описанного четырехугольника

Описанная окружность

Свойство вписанного четырехугольника

Решение задач по теме «Окружность»

Знать утверждения задач 724, 729 и уметь их применять при решении задач типа 698 - 700, 708.

Повторительно-обобщающий урок, решение задач

Контрольная работа № 5 по теме «Окружность»

Уметь применять все изученные теоремы при решении задач.

Повторение. Решение задач

Четырехугольники. Площадь (решение задач)

Знать: формулировки определений, свойств, признаков: параллелограмма, ромба, трапеции.

Уметь: находить элементы четырехугольника, опираясь на изученные свойства, выполнять чертеж по условию задачи; вычислять площадь четырехугольника.

Подобные треугольники. (решение задач)

Окружность (решение задач)

Итоговая контрольная работа

Уметь применять все изученные факты при решении задач.

Итого часов

Учебно-методическое и материально-техническое обеспечение образовательного процесса

Учебно-методическая литература:

Геометрия 7-9 класс / Л. С. Атанасян. М: Просвещение, 2013 год
Бурмистрова Т.А. Геометрия 7 - 9 классы. Программы общеобразовательных учреждений. М., «Просвещение», 2009.
Н. Ф. Гаврилова. Поурочные разработки по геометрии 8 класс, Москва, «ВАКО», 2005 год
А. П. Ершова, В. В. Голобородько, А. С. Ершова «Самостоятельные и контрольные работы по алгебре и геометрии для 8 класса». Разноуровневые дидактические материалы. М: Илекса, 2002 год.
Б. Г. Зив, В. М. Мейлер «Дидактические материалы по геометрии 8 класс», Москва, «Просвещение», 2009 год
Зив Б.Г. Задачи по геометрии. 7-11 классов. - 1995,624с.
Шарыгин И.Ф. Геометрия 7-9 кл. - М.: Дрофа, 1997. - 352с.
Дорофеев Г. В. и др. Оценка качества подготовки выпускников основной школы по математике. М., «Дрофа», 2001.
Стандарт основного общего образования по математике//«Вестник образования» -2004 - № 12 - с.107-119.
Изучение геометрии в 7-9 кл.: Методические рекомендации для учителя/ Л.С.Атанасян, В.Ф.Бутузов и др.- М.: Просвещение;
Геометрия 8 класс. Поурочные планы по учебнику «Геометрия»8 класс. М.Г.Гиляров-Волгоград,2003
Контрольные работы, тесты, диктанты по геометрии 8 класс А.В.Фарков - М.: Экзамен,2006

Для информационно-компьютерной поддержки учебного процесса предполагается использование следующих программно-педагогических средств, реализуемых с помощью компьютера:

1. CD «1С: Репетитор. Математика» (К и М)

2. «Математика, 5-11»

Для обеспечения плодотворного учебного процесса предполагается использование информации и материалов следующих Интернет - ресурсов:

Министерство образования РФ: www.innformika.ru /; www.ed.gov.ru/; www.edu/ru/
Тестирование 5 - 11 классы: www.kokch.ru/cdo/
Педагогическая мастерская, уроки в Интернет и многое другое: teacher.fio.ru
Новые технологии в образовании: edu.secna.ru/main/
Путеводитель «В мире науки» для школьников: www.uic.ssu.samara.ru/nauka/
Мегаэнциклопедия Кирилла и Мефодия: mega.km.ru
Сайты «Энциклопедий», например: www.rubicon.ru/; www.encyclopedia.ru</</font>

Электронные учебные пособия:

Интерактивная математика. 5-9 класс. Электронное учебное пособие для основной школы. М., ООО «Дрофа», ООО «ДОС»,, 2002.
Математика. Практикум. 5-11 классы. Электронное учебное издание. М., ООО «Дрофа», ООО «ДОС», 2003.
Мультимедийное пособие «Живая геометрия». Наглядные чертежи геометрических фигур и геометрических тел. В данной среде возможны быстрые изменения в чертежах и рисунках, что позволяет сделать чертеж подвижным, наглядным, более понятным.
Электронные учебники. (Образовательная коллекция. Плпниметрия 7-9) Используются в качестве виртуальных лабораторий при проведении практических занятий, уроков введения новых знаний. В них заключен большой теоретический материал, много тренажеров, практических и исследовательских заданий, справочного материала. На любом из уроков возможно использование компьютерных устных упражнений, применение тренажера устного счета, что активизирует мыслительную деятельность учащихся, развивает вычислительные навыки, так как позволяет осуществить иной подход к изучаемой теме.

⇧

⇩

скачать материал