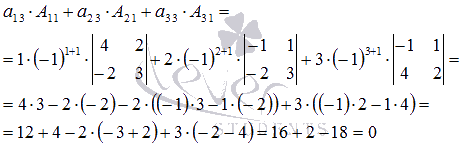Конспект урока по теме Вычисление определителя матрицы

Тема урока: «Вычисление определителя матрицы»

Цели:

- выявить качество усвоения учащимися знаний и способов действий по теме «Матрицы»;

- создать условия для развития способности учащихся к оценочным действиям;

- содействовать развитию вычислительных навыков учащихся, логического мышления, способности к самоконтролю, самооценке, рефлексии.

Тип урока: комбинированный.

Структура урока.

1) Организационный этап.

2) Постановка цели и задач урока. Мотивация учебной деятельности учащихся.

3) Актуализация знаний.

4) Изучение нового материала.

5) Закрепление изученного материала.

6) Подведение итогов.

7) Домашнее задание.

1. Организационный этап.

Приветствия учащихся; проверка их явки и готовности аудитории к уроку.

2. Постановка цели и задач урока.

Сообщает тему и цели практического занятия. Слушают, записывают в тетрадь.

3. Актуализация знаний.

Учащимся необходимо за 2 минуты записать в тетради как можно больше понятий и определений по изученной нами теме "Матрицы".

1. Что называется прямоугольной матрицей?

2. Какая матрица называется квадратной?

3. Какую диагональ квадратной матрицы называют главной?

4. Какая матрица называется единичной?

5. Какие матрицы называются равными?

6. Что называется суммой двух матриц?

7. Какие две матрицы можно перемножить?

8. Какая матрица называется транспонированной?

9. Что такое ранг матрицы?

10. Какие элементарные преобразования можно выполнять над строками матрицы?

11. Перечислите основные свойства определителей.

12. Что такое обратная матрица?

13. Что называется алгебраическим дополнением элемента матрицы?

4. Изучение нового материала.

Понятие определителя является одним из основных в курсе линейной алгебры. Это понятие присуще ТОЛЬКО КВАДРАТНЫМ МАТРИЦАМ, этому понятию и посвящена данная статья. Здесь мы будем говорить об определителях матриц, элементами которых являются действительные (или комплексные) числа. В этом случае определитель есть действительное (или комплексное) число. Все дальнейшее изложение будет ответом на вопросы как вычислять определитель, и какими свойствами он обладает.

Сначала дадим определение определителя квадратной матрицы порядка n на n как сумму произведений перестановок элементов матрицы. На основании этого определения запишем формулы для вычисления определителей матриц первого, второго, третьего порядков и подробно разберем решения нескольких примеров.

Далее перейдем к свойствам определителя, которые будем формулировать в виде теорем без доказательства. Здесь будет получен метод вычисления определителя через его разложение по элементам какой-либо строки или столбца. Этот метод позволяет свести вычисление определителя матрицы порядка n на n к вычислению определителей матриц порядка 3 на 3 или меньшего. Обязательно покажем решения нескольких примеров.

В заключении остановимся на вычислении определителя методом Гаусса. Этот метод хорош при нахождении значений определителей матриц порядка выше 3 на 3, так как требует меньших вычислительных усилий. Также разберем решение примеров.

Определение определителя матрицы, вычисление определителя матрицы по определению.

Напомним несколько вспомогательных понятий.

Определение.

Перестановкой порядка n называется упорядоченный набор чисел, состоящий из nэлементов.

Для множества, содержащего n элементов, существует n! (n факториал) перестановок порядкаn. Перестановки отличаются друг от друга лишь порядком следования элементов.

Например, рассмотрим множество, состоящее из трех чисел: . Запишем все перестановки (всего их шесть, так как ):

Определение.

Инверсией в перестановке порядка n называется всякая пара индексов p и q, для которой p-ый элемент перестановки больше q-ого.

В предыдущем примере инверсией перестановки 4, 9, 7 является пара p=2, q=3, так как второй элемент перестановки равен 9 и он больше третьего, равного 7. Инверсией перестановки 9, 7, 4будут три пары: p=1, q=2 (9>7); p=1, q=3 (9>4) и p=2, q=3 (7>4).

Нас будет больше интересовать количество инверсий в перестановке, а не сама инверсия.

Пусть - квадратная матрица порядка n на n над полем действительных (или комплексных) чисел. Пусть - множество всех перестановок порядка n множества . Множество содержит n! перестановок. Обозначим k-уюперестановку множества как , а количество инверсий в k-ойперестановке как .

Определение.

Определитель матрицы А есть число, равное

.

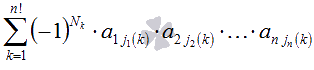Опишем эту формулу словами. Определителем квадратной матрицы порядка n на n является сумма, содержащая n! слагаемых. Каждое слагаемое представляет собой произведение nэлементов матрицы, причем в каждом произведении содержится элемент из каждой строки и из каждого столбца матрицы А. Перед k-ым слагаемым появляется коэффициент (-1), если элементы матрицы А в произведении упорядочены по номеру строки, а количество инверсий в k-ой перестановке множества номеров столбцов нечетно.

Определитель матрицы А обычно обозначается как , также встречается обозначение det(A). Также можно услышать, что определитель называют детерминантом.

Итак,

.

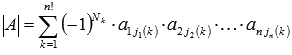Отсюда видно, что определителем матрицы первого порядка является элемент этой матрицы .

Вычисление определителя квадратной матрицы второго порядка - формула и пример.

Найдем определитель квадратной матрицы 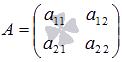порядка 2 на 2 в общем виде.

В этом случае n=2, следовательно, n!=2!=2.

Оформим в виде таблицы необходимые данные для применения формулы

.

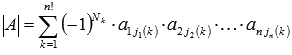Имеем

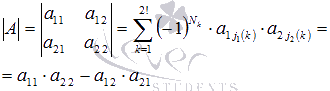
Таким образом, мы получили формулу для вычисления определителя матрицы порядка 2 на 2, она имеет вид .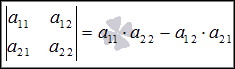

Вычисление определителя квадратной матрицы третьего порядка - формула и пример.

Найдем определитель квадратной матрицы 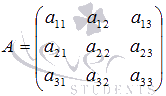порядка 3 на 3 в общем виде.

В этом случае n=3, следовательно, n!=3!=6.

Оформим в виде таблицы необходимые данные для применения формулы

.

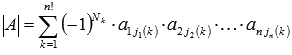Имеем

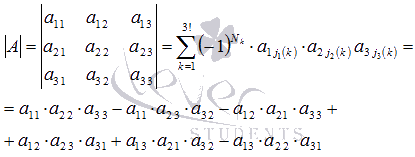
Таким образом, мы получили формулу для вычисления определителя матрицы порядка 3 на 3, она имеет вид

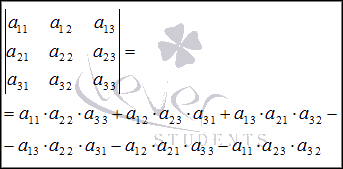
Аналогично можно получить формулы для вычисления определителей матриц порядка 4 на 4, 5на 5 и более высоких. Они будут иметь очень громоздкий вид.

Свойства определителя матрицы, вычисление определителя матрицы с использованием свойств.

На основании озвученного определения справедливы следующие свойства определителя матрицы.

1. Определитель матрицы А равен определителю транспонированной матрицы А^Т, то есть, .

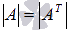2. Если в квадратной матрице все элементы хотя бы одной из строк (одного из столбцов) нулевые, определитель такой матрицы равен нулю.

Действительно, определитель матрицы с нулевым столбцом равен нулю.

3. Если переставить местами две любые строки (столбца) в квадратной матрице, то определитель полученной матрицы будет противоположен исходному (то есть, изменится знак).

4. Если в квадратной матрице хотя бы две строки (два столбца) одинаковы, то ее определитель равен нулю.

5. Если в квадратной матрице все элементы какой-либо строки (столбца) умножить на некоторое число k, то определитель полученной матицы будет равен определителю исходной матрицы, умноженному на k. Например,
   
   

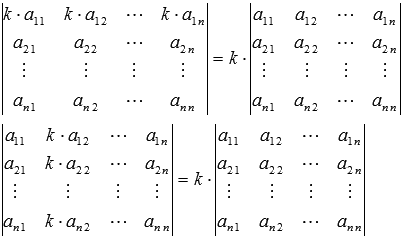
ОБРАТИТЕ ВНИМАНИЕ.

Не путайте и не смешивайте понятия матрицы и определителя! Рассмотренное свойство определителя матрицы и операция умножения матрицы на число это далеко не одно и то же.

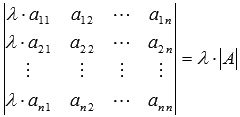, но .

6. Если все элементы какой-либо строки (столбца) квадратной матрицы представляют собой сумму s слагаемых (s - натуральное число, большее единицы), то определитель такой матрицы будет равен сумме s определителей матриц, полученных из исходной, если в качестве элементов строки (столбца) оставить по одному слагаемому. Например,
   
   

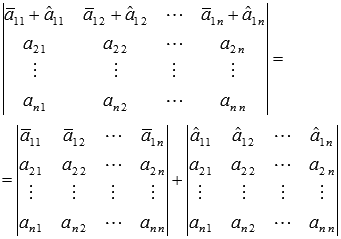
7. Если к элементам некоторой строки (столбца) матрицы прибавить соответствующие элементы другой строки (столбца), умноженные на произвольное число k, то определитель полученной матрицы будет равен определителю исходной матрицы.

8. Определитель квадратной матрицы равен сумме произведений элементов какой-либо строки (столбца) на ихалгебраические дополнения.
   
   

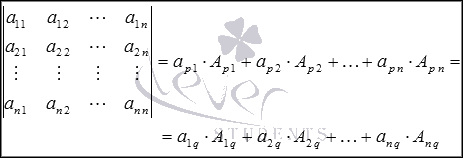
Здесь - алгебраическое дополнение элемента матрицы , .

Это свойство позволяет вычислять определители матриц порядка выше чем 3 на 3путем сведения их к сумме нескольких определителей матриц порядка на единицу ниже. Иными словами - это рекуррентная формула вычисления определителя квадратной матрицы любого порядка. Рекомендуем ее запомнить в силу достаточно частой применимости.

Разберем несколько примеров.

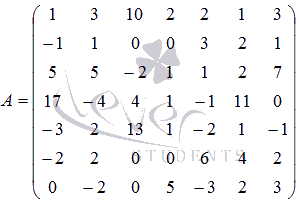порядка 7 на 7.

Решение.Следует отметить, что рассмотренное свойство позволяет вычислить определители матриц любых порядков, однако приходится выполнять массу вычислительных операций. В большинстве случаев определитель матриц порядка выше третьего выгоднее находить методом Гаусса, который мы рассмотрим ниже.

9. Сумма произведений элементов какой-либо строки (столбца) квадратной матрицы на алгебраические дополнения соответствующих элементов другой строки (столбца) равна нулю.
   
   

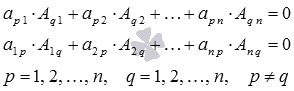
10. Определитель произведения квадратных матриц одного порядка равен произведению их определителей, то есть, 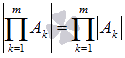, где m - натуральное число большее единицы, A_k, k=1,2,…,m - квадратные матрицы одного порядка.

</ Подведем итог.

Определителем квадратной матрицы, элементы которой есть числа, является число. Мы рассмотрели три способа вычисления определителя:

1. через сумму произведений сочетаний элементов матрицы;

2. через разложение определителя по элементам строки или столбца матрицы;

3. методом приведения матрицы к верхней треугольной (методом Гаусса).

Были получены формулы для вычисления определителей матриц порядка 2 на 2 и 3 на 3.

Мы разобрали свойства определителя матрицы. Некоторые из них позволяют быстро понять, что определитель равен нулю.

При вычислении определителей матриц порядка выше 3 на 3 целесообразно использовать метод Гаусса: выполнить элементарные преобразования матрицы и привести ее к верхней треугольной. Определитель такой матрицы равен произведению всех элементов, стоящих на главной диагонали.

5. Закрепление изученного материала.

Пример.

Убедитесь, что определитель 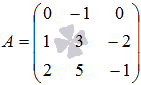матрицы равен определителю транспонированной матрицы.

Решение.

Воспользуемся формулой для вычисления определителя матрицы порядка3 на 3:

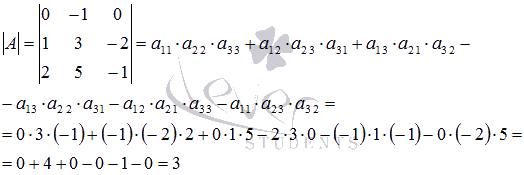
Транспонируем матрицу А:

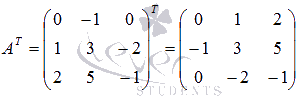
Вычислим определитель транспонированной матрицы:

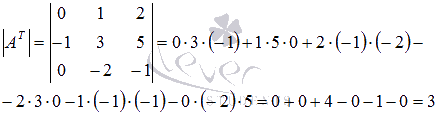
Действительно, определитель транспонированной матрицы равен определителю исходной матрицы.

Пример.

Проверьте, что определитель матрицы 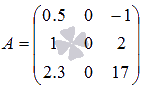порядка 3 на 3равен нулю.

Решение.

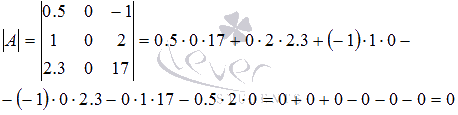
Пример.

Даны две квадратные матрицы порядка 3 на 3 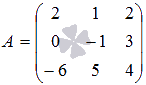и 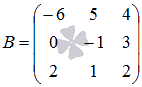. Покажите, что их определители противоположны.

Решение.

Матрица В получена из матрицы А заменой третьей строки на первую, а первой на третью. Согласно рассмотренному свойству определители таких матриц должны отличаться знаком. Проверим это, вычислив определители по известной формуле.

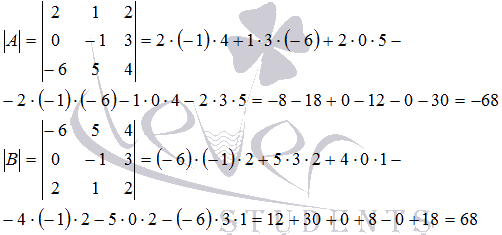
Действительно, .

Пример.

Покажите, что определитель матрицы 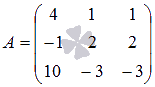равен нулю.

Решение.

В данной матрице второй и третий столбцы одинаковы, так что согласно рассмотренному свойству ее определитель должен быть равен нулю. Проверим это.

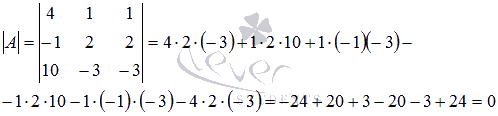
На самом деле определитель матрицы с двумя одинаковыми столбцами есть ноль.

Пример.

Докажите, что определитель 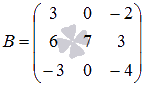матрицы равен утроенному определителю матрицы .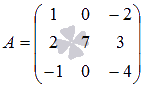

Решение.

Элементы первого столбца матрицы В получены из соответствующих элементов первого столбца матрицы А умножением на 3. Тогда в силу рассмотренного свойства должно выполняться равенство . Проверим это, вычислив определители матриц А и В.

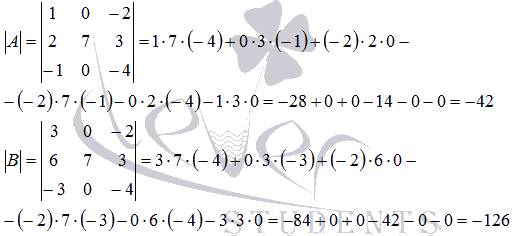
Следовательно, , что и требовалось доказать.

Пример.

Докажите, что определитель матрицы 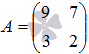равен сумме определителей матриц .

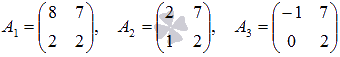Решение.

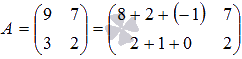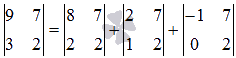В нашем примере , поэтому в силу рассмотренного свойства определителя матрицы должно выполняться равенство . Проверим его, вычислив соответствующие определители матриц порядка 2 на 2 по формуле .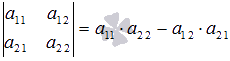

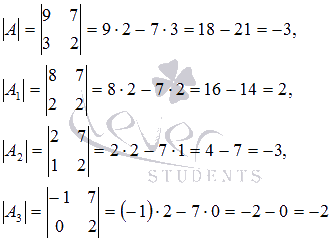
Из полученных результатов видно, что . На этом доказательство завершено.

Пример.

Убедитесь, что если к элементам третьего столбца матрицы 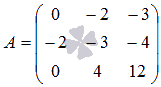прибавить соответствующие элементы второго столбца этой матрицы, умноженные на ( -2 ), и прибавить соответствующие элементы первого столбца матрицы, умноженные на произвольное действительное число , то определитель полученной матрицы будет равен определителю исходной матрицы.

Решение.

Если отталкиваться от рассмотренного свойства определителя, то определитель матрицы, полученной после всех указанных в задаче преобразований, будет равен определителю матрицы А.

Сначала вычислим определитель исходной матрицы А:

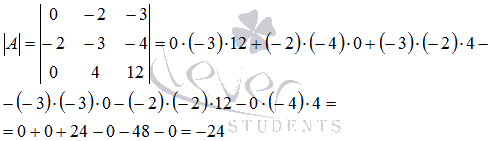
Теперь выполним необходимые преобразования матрицы А.

Прибавим к элементам третьего столбца матрицы соответствующие элементы второго столбца матрицы, предварительно умножив их на (-2). После этого матрица примет вид:

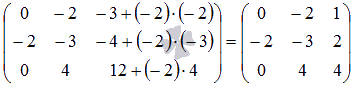
К элементам третьего столбца полученной матрицы прибавим соответствующие элементы первого столбца, умноженные на :

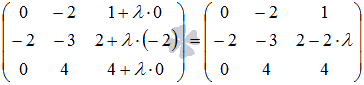
Вычислим определитель полученной матрицы и убедимся, что он равен определителю матрицы А, то есть, -24:

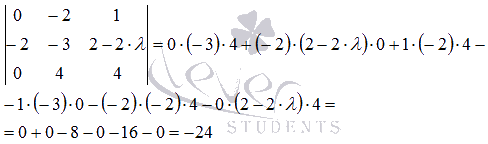
Пример.

Вычислите определитель матрицы 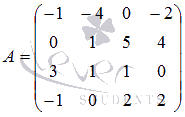порядка 4 на4, разложив его

• по элементам 3-ей строки,

• по элементам 2-ого столбца.

Решение.

Используем формулу разложения определителя по элементам 3-ей строки

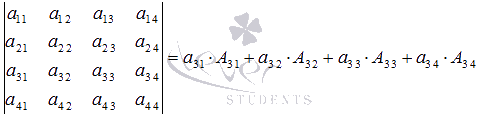
Имеем

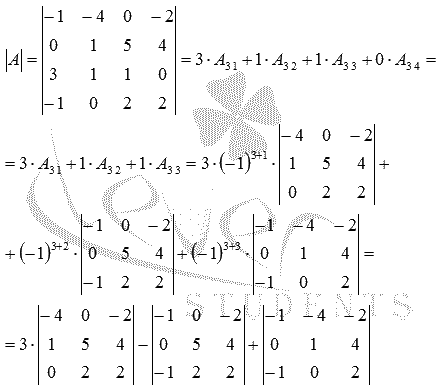
Так задача нахождения определителя матрицы порядка 4 на 4 свелась к вычислению трех определителей матриц порядка 3 на 3:

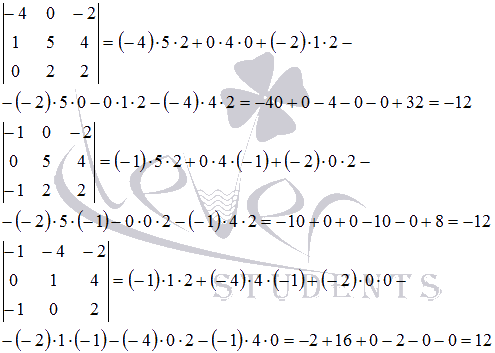
Подставив полученные значения, приходим к результату:

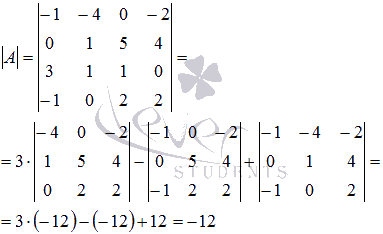
Используем формулу разложения определителя по элементам 2-огостолбца



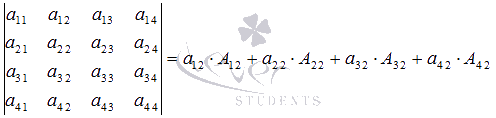
и действуем аналогично.

Не будем подробно расписывать вычисление определителей матриц третьего порядка.

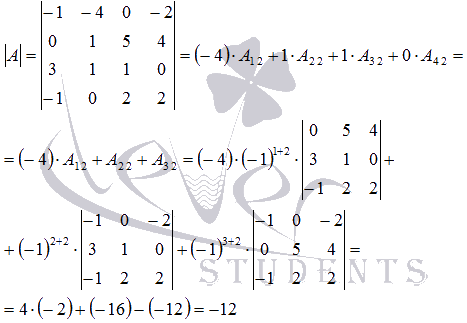
Пример.

Вычислите определитель матрицы 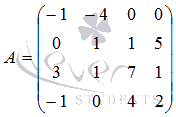порядка 4 на 4.

Решение.

Можно разложить определитель матрицы по элементам любого столбца или любой строки, однако выгоднее выбирать строку или столбец, содержащую наибольшее количество нулевых элементов, так как это поможет избежать лишних вычислений. Разложим определитель по элементам первой строки:

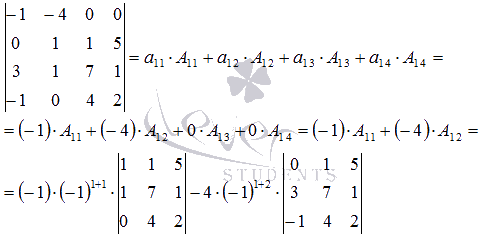
Вычислим полученные определители матриц порядка 3 на 3 по известной нам формуле:

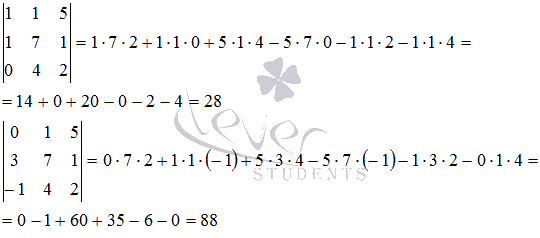
Подставляем результаты и получаем искомое значение

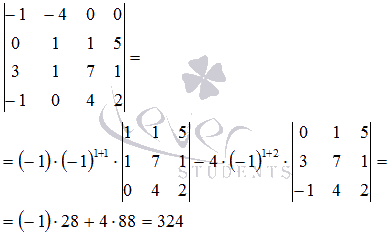
Пример.

Вычислите определитель матрицы 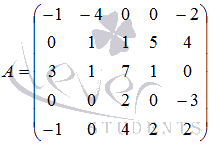порядка 5на 5.

Решение.

В четвертой строке матрицы наибольшее количество нулевых элементов среди всех строк и столбцов, поэтому целесообразно разложить определитель матрицы именно по элементам четвертой строки, так как в этом случае нам потребуется меньше вычислений.

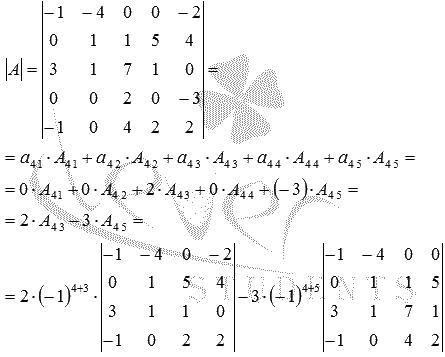
Полученные определители матриц порядка 4 на 4 были найдены в предыдущих примерах, так что воспользуемся готовыми результатами:

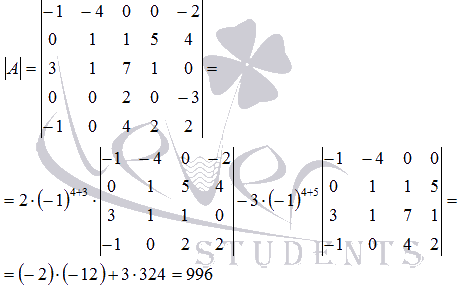
Пример.

Вычислите определитель матрицы

Не следует сразу бросаться раскладывать определитель по элементам какой либо строки или столбца. Если внимательно посмотреть на матрицу, то можно заметить, что элементы шестой строки матрицы можно получить умножением соответствующих элементов второй строки на двойку. То есть, если к элементам шестой строки прибавить соответствующие элементы второй строки, умноженные на (-2), то определитель не изменится в силу седьмого свойства, а шестая строка полученной матрицы будет состоять из нулей. Определитель такой матрицы равен нулю по второму свойству.

Ответ:

.

Пример.

Вычислите определитель квадратной матрицы 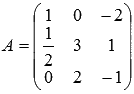порядка 3 на 3.

Решение.

В нашем примере

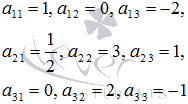
Применяем полученную формулу для вычисления определителя матрицы третьего порядка:

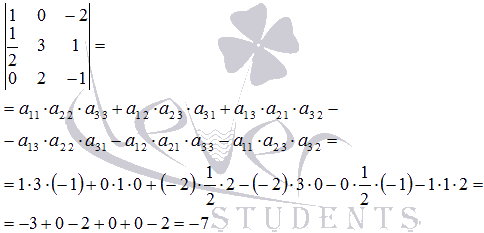
Формулы для вычисления определителей квадратных матриц второго и третьего порядков очень часто применяются, так что рекомендуем их запомнить.

Пример.

Вычислите определитель квадратной матрицы 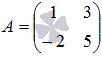порядка .

Решение.

В нашем примере . Применяем полученную формулу :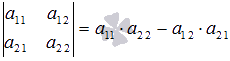

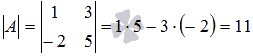
6. Подведение итогов.

Определителем квадратной матрицы, элементы которой есть числа, является число. Мы рассмотрели три способа вычисления определителя:

4. через сумму произведений сочетаний элементов матрицы;

5. через разложение определителя по элементам строки или столбца матрицы;

6. методом приведения матрицы к верхней треугольной (методом Гаусса).

Были получены формулы для вычисления определителей матриц порядка 2 на 2 и 3 на 3.

Мы разобрали свойства определителя матрицы. Некоторые из них позволяют быстро понять, что определитель равен нулю.

При вычислении определителей матриц порядка выше 3 на 3 целесообразно использовать метод Гаусса: выполнить элементарные преобразования матрицы и привести ее к верхней треугольной. Определитель такой матрицы равен произведению всех элементов, стоящих на главной диагонали.

7. Домашнее задание.

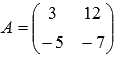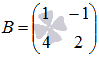1. Убедитесь, что определитель произведения двух матриц и равен произведению их определителей.

Решение.

Найдем сначала произведение определителей матриц А и В:

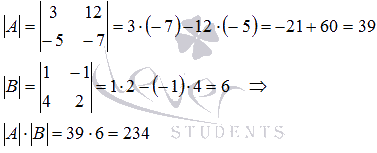
Сейчас выполним умножение матриц и вычислим определитель получившейся матрицы:

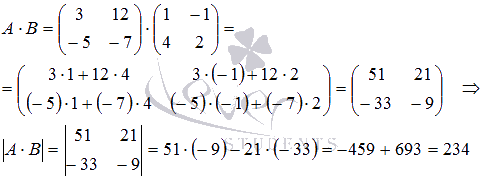
Таким образом, , что и требовалось показать.

2. Покажите, что сумма произведений элементов третьего столбца матрицы 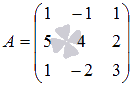на алгебраические дополнения соответствующих элементов первого столбца равна нулю.

Решение.