- Учителю
- Урок алгебры в 9 классе «Последовательности»
Урок алгебры в 9 классе «Последовательности»























Поремская И.В., учитель математики
КГУ «Средняя школа №2 г. Тайынша»
Северо-Казахстанская область
Урок алгебры в 9 классе.
Тема: Последовательности.
Цель урока: обобщение знаний по данной теме.
Задачи:
-
Обучающая - закрепить умения применять формулы при решении задач и проверка прочности знаний;
-
Развивающая - расширить кругозор, развивать логическое мышление, вычислительных навыков и сообразительности;
-
Воспитывающая - прививать интерес к предмету, формировать объективность при оценке ответов товарищей.
Тип урока: контрольно-обобщающий.
Если вы хотите участвовать в большой жизни, то заполняйте свою голову математикой, пока есть к тому возможность.
М. И. Калинин.
Ход урока.
-
Мотивация и сообщение темы урока.
Ребята, сегодня у нас завершающий урок по теме: Последовательности. Вы должны показать свои знания и применить эти знания на практике, при решении задач.
-
Применение знаний в стандартной ситуации.
-
Проверочная работа с взаимопроверкой.
-
Для данной последовательности запиши формулу n-го члена.
-
2; 4; 6 . . . аn=2n
-
1; 3; 5 . . . аn=2n-1
-
1;
 ;
;  ;
;  ;
;  . . . аn=
. . . аn= 1≤ n ≤5
1≤ n ≤5
-
Запиши в виде рекуррентной формулы.
-
Каждый член последовательности равен разности предыдущего члена и числа 15. аn+1=аn-15
-
Каждый член последовательности равен произведению двух предшествующих членов. аn+1=аn ∙ аn-1
-
Каждый член последовательности получают путем деления предыдущего члена на 2. аn+1=

(текст проверочной работы проектируются графопроектором на экране. И ответы проектируются).
Проверочная работа.
-
Для данной последовательности запиши формулу n-го члена.
-
2; 4; 6.
-
1; 3; 5.
-
1;
 ;
;  ;
;  ;
;  .
.
-
Запиши в виде рекуррентной формулы:
-
Каждый член последовательности равен разности предыдущего члена и числа 15;
-
Каждый член последовательности равен произведению двух предшествующих членов;
-
Каждый член последовательности получают путем деления предыдущего члена на 2.
Ответы:
-
1. аn=2n
-
аn=2n-1
-
аn=
 1≤ n ≤5
1≤ n ≤5
-
1. аn+1=аn-15
-
аn+1=аn ∙ аn-1
-
аn+1=

Ребята проверяют ответы друг у друга и сразу же оценивают.
«5» - 6 ответов
«4» - 5 ответов
«3» - 3, 4 ответа
«2» - до 3-х ответов.
-
Сообщение о числах Фибоначчи.
Леонардо Фибоначчи - великий итальянский математик. Последовательностью числе Фибоначчи называется такая последовательность, у которой член равен сумме двух предыдущих, а первые два числа последовательности 0 и 1.
аn+1=аn + аn-1
0; 1; 1; 2; 3; 5; 8; 13; 21; 34; 55; 89 . . .
Эта последовательность имеет очень интересное свойство, как и числа арифметической и геометрической прогрессии.
аn-1 ∙ аn+1 - аn2 =±1
Н-р: 2; 3; 5 3; 5; 8
2 ∙ 5 - 32 = 1 3 ∙ 8 - 52 = - 1
(В это время один из учащихся заполняет открытый лист учета).
-
Применение знаний в нестандартной ситуации.
-
Проверка знаний определений и формул. На доске двое учащихся записывают формулы, которые нужны при решении задач с использованием арифметической и геометрической прогрессий.
Остальные учащиеся работают устно, проверяются определения арифметической и геометрической прогрессии.
-
Историческая справка об истории развития арифметической и геометрической прогрессиях.
-
Решение задач.
Устная работа:
1. определение ариф. прогрессии
2. определение геом. прогрессии
3. определить данная последовательность является ариф. или геом. прогрессией
-
 ;
;  ; 1; . . . (геом. пр. q=2)
; 1; . . . (геом. пр. q=2) -
 ;
;  ; . . . (геом. пр. q=
; . . . (геом. пр. q=
-
3; 7; 11; . . . (ариф. пр. d=4)
-
5; 10; . . . если a3=15 (ариф. пр.d=5)
если b3=20 (геом. пр. q=2)
Задача №1.
При свободном падении тело проходит в первую секунду 4,9 м, а в каждую следующую на 9,8 м больше. Найдите глубину шахты, если свободно падающее тело достигло ее дна через 5 сек после начала падения?
Решение:
а1=4,9 а5=а1+4d=4,9+4∙9,8=44,1 (м)
d=9,8
a5=?
Ребята, где еще на практике можно применить способ решения задачи?
(найти глубину оврага, глубину впадины, высоты башни, высоту многоэтажного дома).
Задача №2.
В огороде 30 грядок, каждая длиной 16 м и шириной 2,5 м. поливая грядки, огородник приносит ведра с водой из колодца, расположенного в 14 м от края огорода и обходит грядки по меже, причем воды, приносимой за один раз, достаточно для поливки только одной грядки. Какой длины путь огородника при поливке всего огорода? Путь начинается и заканчивается у колодца.
Колодец16м 14м
2,5м
Решение:
1 грядка 14+16+2,5+16+2,5+14=65 м
2 грядка 14+2,5+16+2,5+16+2,5+2,5+14=65+5=70 м
При поливе каждой следующей грядки требуется пройти на 5 м больше.
Колодец16м 14м
65 (м)2,5м 14 м
2,5м
16 м
70 (м)
75 (м)
65+29 ∙ 5 (м)
а1=65 S30= ∙ 30=4125 (м)
∙ 30=4125 (м)
d=5
S30=?
Ребята, летом каждый из вас может посчитать, сколько потребуется пройти километров, чтобы полить свой огород.
Задача №3.
Некто продал лошадь за 156 руб. Но покупатель, приобретая лошадь, раздумал ее покупать и возвратил продавцу, говоря: «Нет мне расчета покупать за эту цену лошадь, которая таких денег не стоит». Тогда продавец предложил другие условия: «Если цена лошади высока, то купи ее только подковные гвозди, а лошадь получишь придачу бесплатно. Гвоздей в каждой подкове 6. За первую гвоздь дай мне 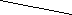 к, за второй 2к, за третий 1к и т.д.
к, за второй 2к, за третий 1к и т.д.
Покупатель, соблазненный низкой ценой и желая даром получить лошадь, принял условия продавца, рассчитывая, что придется уплатить не более 10 руб. Насколько покупатель проторговался?
Решение:
b1= 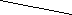 q=2 S24=
q=2 S24=  =
= 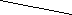 (
( )=4194303,8 (к) ≈ 42000 (руб)
)=4194303,8 (к) ≈ 42000 (руб)
n=24
S24=?
Так, что ребята, когда будете покупать, например, куртку или шубу, не покупайте заклепки и пуговицы от них.
Задача №4 (игровая).
От стола учителя до двери 3 м. один из учеников идет от стола до двери по прямой. Первый шаг он делает длиной 1 м, второй  м, третий
м, третий 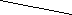 м и т.д., так чтобы длина следующего шага была в 2 раза меньше предыдущего. Дойдет ли ученик до двери или нет?
м и т.д., так чтобы длина следующего шага была в 2 раза меньше предыдущего. Дойдет ли ученик до двери или нет?
1 +  +
+ 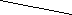 +
+  + . . .бесконечно убывающая геометрическая прогрессия.
+ . . .бесконечно убывающая геометрическая прогрессия.
Решение:
1 +  +
+ 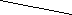 +
+  + . . .+
+ . . .+
B1=1 q=
Sn= =
=  =
=  = 2 (
= 2 (
При n→∞;  →0; |q|<1
→0; |q|<1
Sn=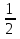 =
=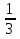 =2
=2
Если выполним все условия, то не дойдем до двери.
А как нужно изменить условия, чтобы дойти до порога? (сделать первых два шага по 1 м)
Задача №5 (игровая).
Шары расположены в форме треугольника, в первом ряду - 1 шар, во второй - 2 шара и т.д
Во сколько рядов расположены 120 шаров?
Сколько шаров нужно, чтобы составить 30 рядов?
Решение:
a1=1 a2=2 d=1
S30 = 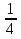 ∙ 30=
∙ 30= 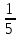 ∙ 30=465
∙ 30=465
S30 =  ∙ 30=
∙ 30= 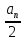 ∙ 30=465
∙ 30=465
Ответ: 465 шаров нужно, Чтобы составить 30 рядов.
Sn =120
120=  ∙ n
∙ n
(2+n-1)∙ n=240 n1=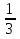 =15
=15
n2+ n-240=0 n2= =-16 (от)
=-16 (от)
Д=1+960=961
Ответ: 15 рядов
-
Контроль знаний:
-
Контрольный тест с выбором ответа.
-
Взаимопроверка и выставление оценок в открытый лист учета.
Контрольный тест.
I вариант
-
Вырази а8 через а1 и d.
А) а8=а1+7 d
Б) а8=а1∙ d7
В) а8=а1+8 d
-
b2= 33; b3=44
q=?
А) 11 Б)  В) 1
В) 1
-
а1=3; d=2
а5=?
А) 8 Б) 11 В) 14
-
-2, 1 . . . - геом. прогрессия
Найти 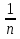
А) - 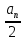 Б)
Б) 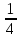 В)
В)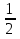
-
2; 7 . . . - ариф. прогрессия
Найти сумму членов с третьего по девятый включительно.
А) 198 Б) 189 В) 9
II вариант
-
Вырази b6 через b1 и q.
А) b6= b1+ q6
Б) b6= b1∙ q5
В) b6= b1∙ q6
-
а4=15; а5=10
d=?
А) 5 Б) - 5 В) 1,5
-
b1= 18; q=
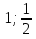
b2=?
А) 2 Б)  В) 18
В) 18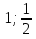
-
-2, 1 . . . - ариф. прогрессия
Найти а12 - а6
А) 6 Б) 18 В) 13
-
32; 16 . . . - геом. прогрессия
Найти сумму членов с третьего по шестой включительно.
А) 63 Б) 48 В) 15
Ответы:
I вариант
-
1. А
-
2. В
-
3. Б
-
4. В
-
5. Б
II вариант
-
1. Б
-
2. Б
-
3. А
-
4. Б
5. В
-
Подведение итогов.
-
Д\з. повт. п. 1, 2, 5, 7.