Максимова РП

Иркутский авиационный техникум

ПРАКТИЧЕСКАЯ РАБОТА по теме « Производная функции»

Цель. Научиться дифференцировать функции одного переменного

Задачи. Выучить правила дифференцирования функций. Научиться решать задачи на применение производной

Формирование компетенций ОК2, ОК 6

Оборудование: компьютер, презентации, учебник Алгебра и начала анализа: уч. для 10 - 11 кл общеобразовательных учреждений/ [ Ш.А. Алимов , Ю.М. Колягин и др.].-18 изд.- М.: Просвещение, 2012.- 465 с

Ход работы:

1. Познакомиться с теоретическим материалом

2. Сделать краткий конспект теоретического материала в рабочих тетрадях (основные понятия, определения, формулы, примеры)

3. В тетрадях для практических работ выполнить самостоятельную работу или решить номера, которые указаны в работе.

4. Сдать преподавателю тетради для практических работ.

Критерии оценивания практической работы

Оценка «5» ставится, если верно и рационально решено 91% -100% предлагаемых заданий, допустим 1 недочет, неискажающий сути решения.

Оценка «4» ставится при безошибочном решении 81% -90% предлагаемых заданий.

Оценка «3» ставится, если выполнено 70% -80% предлагаемых заданий, допустим 1 недочет.

Оценка «2» - решено мене 70% предлагаемых заданий.

Дифференциальное исчисление (производная функции)

Основные понятия. Одним из основных понятий математического анализа является понятие о производной. Производной функции у=f(x) по аргументу х называется предел отношения приращения функции к соответствующему приращению аргумента при условии, что последнее стремиться к нулю. Производная обозначается символами: y', у'_х,f'(х). Таким образом,

(*)

Процесс нахождения производной называется дифференцированием. Продифференцировать данную функцию - значит найти ее производную. Из определения производной непосредственно вытекает общий метод ее нахождения. Числовое значение производной данной функции у = f(х) при данном числовом значении аргумента х=а называется частным значением производной. Это записывается так:

Рассмотрим геометрическое и механическое значение производной. Производная у' = f'(х) при данном значении х=а равна угловому коэффициенту k касательной, проведенной к кривой через данную на ней точку М, абсцисса которой и есть данное значение х=а. Это можно записать та: k = f'(а). Напомним что угловой коэффициент k = tg  , где  есть угол, составленный касательной и положительным направлением оси Ох. Для каждой точки касания угол наклона  имеет свое единственное значение.

Если тело движется по закону S=f(t). где S- путь в метрах, а t- время в секундах, то при изменении времени t на величину t влечет за собой изменение величины S на величину S , то отношение S к t (S/ t ) есть средняя скорость изменения пути по времени t, а именно:

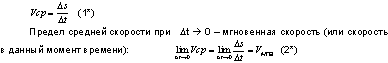
Механический смысл производной: мгновенная скорость неравномерного движения есть производная от функции, выражающей зависимость пройденного пути S от времени t. Если закон прямолинейного движения задан уравнением S=f(t). где S- путь в метрах, а t- время в секундах, то скорость

(при условии, что предел существует) - скорость в данный момент времени или мгновенная скорость. Итак ,v=s_t' = f'(t), т.е. скорость точки в случае прямолинейного движения есть производная от пути по времени.

Формулы дифференцирования основных функций

Производная постоянной величины равна нулю:

c'=0, где c=const. (1)

Производная степенной функции:

(хⁿ)' =nx^n-1., n - действительное число (2)

Производная от аргумента:

х' = 1. (3)

Производная функции вида:

у =

(4)

Производная функции у = 1/х:

Производные тригонометрических функций:

У = sinx

(sinx)'=cosx ( 6)

У = cosx

(cosx)'=-sinx (7)

У = tgx

(tgx)' = (8)

У = сtgx

(ctgx)'= (9)

Формула перехода от десятичных логарифмов к натуральным:

lnN= (10) где 0.4343 = lge.

Формула перехода от натуральных логарифмов к десятичным:

Число называется модулем перехода от десятичных логарифмов к натуральным. (11)

Производная логарифмической функции у = ln x:

(lnx)' = (12)

Производная показательной функции y =a^x:

(a^x)'=a^xlna. (13)

Частный случай y=e^x:

(е^x)' = e^x. (14)

Производные обратных тригонометричеких функций:

(arcsinx)' = (15)

Y = arccos x

(arccosx)' = (16)

Y = arctgx

(arctgx)' = ( 17)

Y = arcctgx

(arcctgx)' = (18)

Основные правила дифференцирования

Производная алгебраической суммы конечного числа функций:

(u+v-w)'=u'+v'-w', (1)

где u, v и w - различные функции от х, имеющие производные по х.

Производная произведений двух функций: (uv)'=u'v+v'u, (2)

где u и v - различные функции от х, имеющие производные по х.

Производная произведения постоянной на функцию: (cu)'=cu', где с=const. (3)

Производная частного (дроби): (4) , где с=const. (5)

где u и v - различные функции от х, имеющие производные по х, считая, что v²0 при том значении аргумента х, при котором находится производная:

Производная сложной функции: если у=f(u), где u = (х), то

у'_х=у'_uu'_x y'_x=f(u)u'_x.(6)

Производные более высокого порядка

Второй производной или производной второго порядка данной функции у=f(x) называется производная от первой производной (или производной от производной первого порядка).

Обозначение второй производной: y'', у_x'_x', f''(x), ^ух².- или "дэ два игрек по дэ икс дважды".

Рассмотрим механическое значение второй производной.

С точки зрения механики, вторая производная от пути по времени есть ускорение прямолинейного движения точки М в данный момент:

(4*)

т.е. ускорение есть первая производная от скорости по времени или вторая производная от пути по времени.

Рассмотрим решение примеров и задач на нахождение производной от заданных функций:

Пример 1. Дана функция . Найти ,,

Решение.

Ответ: =1, =19, =-33

Пример 2. Найти производную функции

Решение: используя формулу (uv) ' = u' v + v' u, (2)

-производная произведения двух функций, получим:

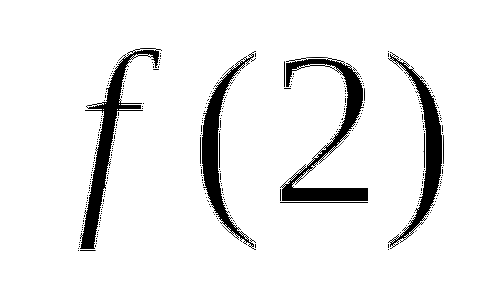Ответ:

Иначе, перемножая двучлены, функцию у=(х+5)(х²-1) можно

записать так: у=х³+5х²-х-5; тогда y'=(x³)'+(5x²)'-x'-5', y'=3x²+10x-1

Ответ: y' = 3x²+10x-1

Пример 3.Найти производную функции

Решение. Перепишем функцию в виде

По формулам (4) - производная алгебраической суммы и (2) - производная степенной функции -

продифференцируем функцию: :

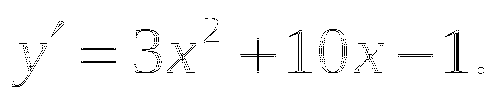
Ответ.

Пример 4. Найти производную функции у=(х²+3)¹⁰.

Решение. Это сложная функция. Пусть х²+3=u, тогда у=u¹⁰. Производная находится по формуле дифференцирования сложной функции:

у'=(u¹⁰)'=10u⁹u'_x, u'_x=(x²+3)'=2x,

y'=10(x²+3)⁹2x, y'=20x(x²+3)⁹.

Ответ: y'=20x(x²+3)⁹.

Пример 5. Продифференцировать функцию y=sin8x.

Решение. Пусть 8х=u, тогда у=sinu.

y'=(sinu)'=cosu*u'_x; u'_x=(8x)'=8

y'=cosu*8 или y'=8cos8x Ответ: у'=8cos 8x.

Пример 6. Найти производную функции

Решение. Пусть , тогда и

,

Ответ:

Пример 7. Продифференцировать функцию у= ln sin x

Решение. sin x = u, y=ln u, тогда

Ответ: .

Пример 8. Дана функция .Найти .

Решение. Найдем производную данной функции:

f'(x) = 2^{x +x+1.} (x²+x+1)'^.ln 2

f'(x) = 2^{x +x+1.}(2x+1)^.ln 2

f'(x) = 2^3.(2^.1+1)^.ln 2 f'(1) = 24ln 2

Ответ: . f'(1) = 24ln 2

Пример 9. Найти производную функции у =

Решение: В данном примере основание и показатель степени

зависят от х. Логарифмируя, получим lny = x²lnx .

Продифференцируем обе части последнего равенства по х.

Так как у' является функцией от х, то lny есть сложная функция х

и (lny)' = y'/y Следовательно,

Ответ:

Задача 1. Точка движется прямолинейно по закону s = 2t³ + t² + 1, где s - путь в метрах, t - время в секундах. Найти величину скорости в момент t = 3c и величину ускорения в момент t = 4c.

Решение. Скорость равна

v = s'_t = (2t³ + t² + 1)' = 6t² + 2t

v_t=3 = 6^.3² + 2^.3 = 60 (м/с)

Ускорение равно

a = v'_t = (6t² + 2t)' = 12t + 2

a_t=4 = 12*^.4 + 2 = 50(м/c²)

Ответ: .v_t=3 = 60м/с, a_t=4 = 50 м/с².

Задача 2. Найти уравнение касательной к параболе у = х² - 4х + 2 в точке, абсцисса которой равна 3.

Решение. Найдем ординату точки касания:

у_х=3 = 3² - 4^*3 + 2 = -1

Итак, точка касания М (3; - 1) найдена. Для нахождения уравнения касательной воспользуемся уравнением пучка прямых у - у₁= k (x- x₁).

В нашем примере х₁ = 3, у₁ = -1, значит у + 1 = k(x - 3).

Угловой коэффициент

k = y'_x=3 = (x² - 4x + 2)'_x=3 - (2x - 4)_x=3 = 2.

Поэтому искомое уравнение касательной примет вид:

у + 1 = 2(х - 3) или у = 2х - 7 в общем виде 2х - у - 7 = 0

Вопросы для самопроверки

1. Дайте определение производной?

2. Что называется касательной прямой к линии в данной ее точке?

3. В чем заключается геометрическое значение производной от данной функции y=f(x) в системе декартовых координат?

4. В чем заключается механическое значение производной первого порядка( производной второго порядка) ?

5. Сформулируйте и докажите теоремы о производной алгебраической суммы, произведения и частного.

6. Сформулируйте и докажите теорему о производной функции от функции (производная сложной функции).

7. Напишите формулы для нахождения производной логарифмической и показательной функций.

8. В чем состоит прием логарифмического дифференцирования?

9. В чем состоит способ параметрического задания функций и уравнений линий? Привести примеры.

10. Указать способ дифференцирования параметрически заданных функций.

11. Какая функция называется дифференцируемой? В чем состоит необходимое условие дифференцируемости функции?

12. Привести примеры непрерывных, но не диффиринцируемых функций.

13. Напишите формулы дифференцирования тригонометрических функций.

14. Напишите формулы дифференцирования обратных тригонометрических функций.

15. Что называется производной второго порядка?

16. В чем заключается механический смысл производной второго порядка (или второй производной)?

17. В каких точках нельзя провести касательные к графикам функций:

a) f(x) = I x-3I; b) f(x) = Ix² - xI c) f(x) = x ^2/3

17. Может ли для четной всюду дифференцируемой функции выполнятся соотношение: а) f '(0) > 0; b) f '(0) < 0; c) f ' (0) = 0?

Задания для самостоятельной работы:

Найдите производные следующих функций:

1) f(x) = x³ (x² - 1)²; 2) f(x) = x⁴ (x² - 1)⁵;

3) y = 8^x; 4) y = sin (2x - 5);

5)

9) Лифт после включения движется по закону s=1,5t² + 2t + 12, где s - путь (в метрах), t - время (в секундах). Найдите скорость лифта в момент времени t=2.

10. Разложение некоторого химического вещества протекает в соответствии с уравнением m = m_oe^-kt, m - количество вещества в момент времени t, k - положительная постоянная. Найдите скорость разложения вещества и выразите ее как функцию времени.

11. Зависимость количества Q вещества, получаемого в химической реакции, от времени t определяется формулой Q=a(1 + be^-kt). Определите скорость реакции и выразите ее как функцию Q .

12. Атмосферное давление воздуха р на высоте над уровнем моря можно вычислить по формуле р = р_ое^-h/a, р_о - давление на уровне моря и а - постоянная. Найдите скорость изменения давления с высотой и выразите ее как функцию р.

13. Размер популяции насекомых в момент времени t (время выражено в днях) задается величиной p(t)= 10000 - 9000(1 + t) ^-1. Вычислите скорость роста популяции p '(t) в момент времени t.

14. Размер популяции бактерий в момент времени t (время выражено в часах) задается формулой p(t)= 10⁶ + 10⁴t - 10³t² . Найдите скорость роста популяции, когда t = 1 час.

15. При прямолинейном движении точки зависимость пути от времени задана уравнением

S = t . Найти ускорение точки в конце 4-й секунды.

Ответы: 1). f^/(x) = 3x² (x² - 1)²+ 2x³ (x² - 1)*2х = x² (x² - 1) (7x² - 3 )

2). f^/(x) = 4x³ (x² - 1)⁵+ 5x³ (x² - 1)⁴*2х = 2x³ (x² - 1)⁴ (2x² - 2+5х )

9) 8 м/с; 10) v = - km; 11) v = -k(Q - a); 12) v = -p/a; 13) p(t) = 9000/(1+t)²;14) 8000 бактерий в час; 15) a = -1/32.

Написать отчет и сдать преподавателю на проверку