Контрольная работа № 7 по теме «Применение производной к исследованию функций»

Контрольная работа № 7 (1 час)

Цели: выявление знаний учащихся, проверка степени усвоения ими изученного материала; развитие навыков самостоятельной работы.

Вариант 1

1. Составьте уравнение касательной к графику функции 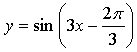в точке

2. Составьте уравнения касательных к графику функции в точках его пересечения с осью абсцисс. Найдите точку ппересечения этих касательных.

3. Исследуйте функцию на монотонность и экстремумы и постройте её график.

4. Найдите значение параметра а, при котором касательная к графику функции в точке с абсциссой параллельна биссектрисе первой координатной четверти.

Вариант 2

1. Составьте уравнение касательной к графику функции 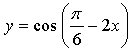в точке

2. Составьте уравнения касательных к графику функции в точках его пересечения с осью абсцисс. Найдите точ-кку пересечения этих касательных.

3. Исследуйте функцию на монотонность и экстремумы и постройте её график.

4. Найдите значение параметра а, при котором касательная к графику функции в точке с абсциссой параллельна прямой

Вариант 3

1. Составьте уравнение касательной к графику функции в точке х = 4.

2. Составьте уравнения касательных к графику функции в точках его пересечения с осью абсцисс. Найдите точку пересечения этих касательных.

3. Исследуйте функцию на монотонность и экстремумы и постройте её график.

4. Найдите значение параметра а, при котором касательная к графику функции в точке с абсциссой параллельна биссектрисе второй координатной четверти.

Вариант 4

1. Составьте уравнение касательной к графику функции в точке х = 1.

2. Составьте уравнения касательных к графику функции в точках его пересечения с осью абсцисс. Найдите точку пересечения этих касательных.

3. Исследуйте функцию на монотонность и экстремумы и постройте её график.

4. Найдите значение параметра а, при котором касательная к графику функции в точке с абсциссой параллельна прямой

Решение вариантов контрольной работы

Вариант 1

1.

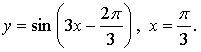
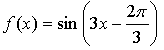
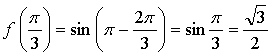
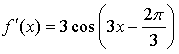
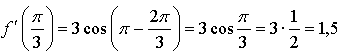
Уравнение касательной:

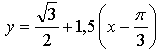
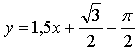
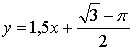
Ответ:

2.

Найдем точки пересечения с осью 0х:

Составим уравнение касательной в точке х = 1:

Получим,

Составим уравнение касательной в точке х = -1:

Получим

Найдем точку пересечения касательных:

х = 0

Ответ: , (0; -6).

3.

1) Область определения:

2) Чётность / нечётность:

- чётная.

3) Асимптоты.

Асимптот нет.

4) Монотонность и экстремумы.

х = 0, х =  1

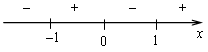
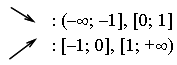
5) Контрольные точки:

4.

Биссектриса первой координатной четверти имеет уравнение у = х. Если касательная ей параллельна, то она имеет такой же угловой коэффициент, то есть k = 1.

Таким образом, нужно найти такое значение параметра а, при котором производная данной функции в точке равна 1.

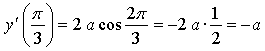
Ответ:

Вариант 2

1.

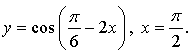
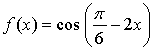
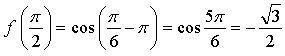
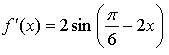
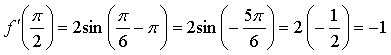
Уравнение касательной:

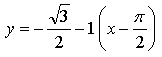
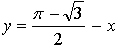
Ответ: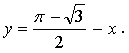

2.

Найдем точки пересечения с осью 0х:

Составим уравнение касательной в точке х = 2:

Получим

Составим уравнение касательной в точке х = -2:

Получим

Найдем точку пересечения касательных:

х = 0

Ответ: (0; -48).

3.

1) Область определения:

2) Чётность / нечётность:

- нечётная.

3) Асимптоты.

Асимптот нет.

4) Монотонность и экстремумы.

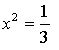
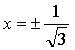
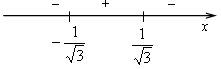
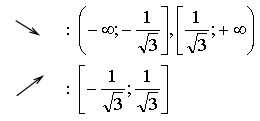
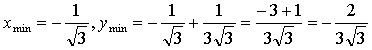
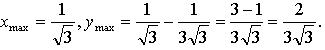
5) Контрольные точки:

Пересечение с осью 0х:

х = 0, х =  1

А (0; 0), В (1; 0), С (-1; 0).

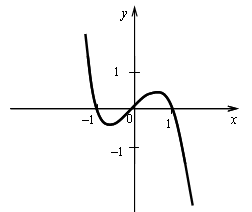
4.

Если касательная параллельна прямой то она имеет такой же угловой коэффициент, то есть Значит, нужно найти такое же значение параметра а, при котором производная данной функции в точке равна

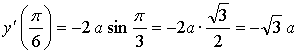
Ответ:

Вариант 3

1. , х = 4.

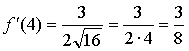
Уравнение касательной:

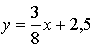
Ответ:

2.

Найдем точки пересечения с осью 0х:

Составим уравнение касательной в точке х = 1:

Получим

Составим уравнение касательной в точке х = -1:

Получим

Найдем точку пересечения касательных:

х = 0

Ответ: (0; -24).

3.

1) Область определения:

2) Чётность / нечётность:

- ни чётная, ни нечётная.

3) Асимптоты.

Асимптот нет.

4) Монотонность и экстремумы.

х = 0, х = 2

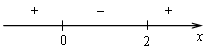
5) Контрольные точки:

4.

Биссектриса второй координатной четверти имеет уравнение у = -х. Если касательная ей параллельна, то она имеет такой же угловой коэффициент, то есть k = -1.

Таким образом, нужно найти такое значение параметра а, при котором производная данной функции в точке равна -1.

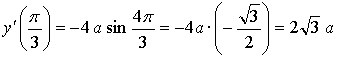
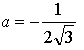
Ответ:

Вариант 4

1. х = 1.

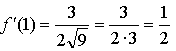
Уравнение касательной:

Ответ:

2.

Найдем точки пересечения с осью 0х:

Составим уравнение касательной в точке х = 1:

Получим

Составим уравнение касательной в точке х = -1:

Получим

Найдем точку пересечения касательных:

х = 0

Ответ: (0; -68).

3. .

1) Область определения:

2) Чётность / нечётность:

- чётная.

3) Асимптоты.

Асимптот нет.

4) Монотонность и экстремумы.

х = 0, х =

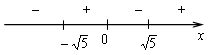
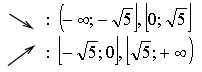
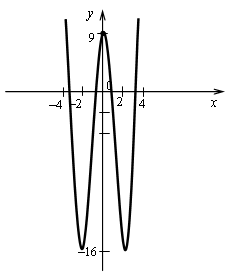
5) Контрольные точки:

4.

Если касательная параллельна прямой то она имеет такой же угловой коэффициент, то есть k = 1. Значит, нужно найти такое же значение параметра а, при котором производная данной функции в точке равна 1.

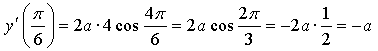
-а = 1

а = -1

Ответ: а = -1.